波、流对库区四柱框架墩连续梁动力响应影响分析

李 杰，王 澳，杨大雨，李思达，张金鹏，张承实

(1.郑州大学 土木工程学院，河南 郑州 450001； 2.河南濮泽高速公路有限公司，河南 郑州 450016；3.中国建筑第七工程局有限公司，河南 郑州 450004)

0 引 言

地震是引起桥梁破坏的主要因素之一.处于库区的桥梁面临着水对结构的作用，特别是地震激励时动水效应的影响显著.当地震发生时，桥墩在深水中产生变形和振动，进而使其附近水体晃动，水体又会对桥墩产生反作用，从而改变桥墩变形和振动状态，这种相互作用贯穿整个地震作用过程.许多学者对深水桥梁在地震作用下流固耦合效应开展了深入研究[1-3]，但地震作用下深水桥梁处于绕射波、水流和地震激励共同产生的辐射波所组成的综合波流场中，桥梁与波流场作用双向耦合，限于理论认识和问题复杂性，多数研究对流体影响简单化处理，忽略了由地震激励产生的辐射波浪对绕射波流场的影响，而对于库区复杂桥墩的桥梁地震响应研究就更少了.因此，针对复杂桥墩库区桥梁在波浪、水流环境中动力响应研究亟待深入.本文以跨黄河小浪底库区某4柱桩柱式框架墩深水桥梁为研究对象，运用有限元软件ANSYS建立桥梁(墩)-水耦合数值分析模型，通过水-桥梁相互作用分析，明确水流、波浪联合作用对动力响应的影响，随后对该桥在无水、静水以及波、流共同作用下地震响应进行分析，探讨波浪、水流和水深对桥梁结构地震响应的影响.

1 依托工程及流固耦合模拟方法

1.1 依托工程

以跨黄河小浪底水库库尾某4柱桩柱式框架墩预应力混凝土连续梁桥为依托，跨径布置(60+13×100+60)m，主梁为C55单箱单室截面，根部梁高 6.3 m，跨中及边墩位置处的梁高 2.8 m；箱梁顶宽 16.25 m，底宽 8.25 m，悬挑长度 4 m；梁高及底板厚均按二次抛物线变化.C40混凝土承台厚度为 4 m.桥墩采用C40混凝土2×2桩柱式框架墩(施工现场见图1)，构造详见图2，4根墩柱编号见图2的B-B截面.最高桥墩 78.865 m，其中h1段 12.865 m 墩直径 2.8 m 立模施工，h2段 66 m 墩直径 3 m 钢护筒施工；在距桩底 84.4 m、100 m、120.6 m 位置分别设置厚度 2.4 m、2.4 m、2.6 m 的3道系梁；与墩一体的基础为4根(2×2布置)直径 2.5 m、长 52 m 钻孔灌注崁岩桩，横桥向两桩间距 6.25 m，顺桥向两桩间距 5 m.针对本文研究目的，同时考虑计算效率和计算能力，将桥梁原设计15跨缩减为5跨，其中2、3、5号墩设置单向活动支座，4号墩设置固定支座，桥墩高度均为 78.865 m ，缩减后结构示意见图3.

图1 桥墩施工实景Fig.1 Real scene of pier construction

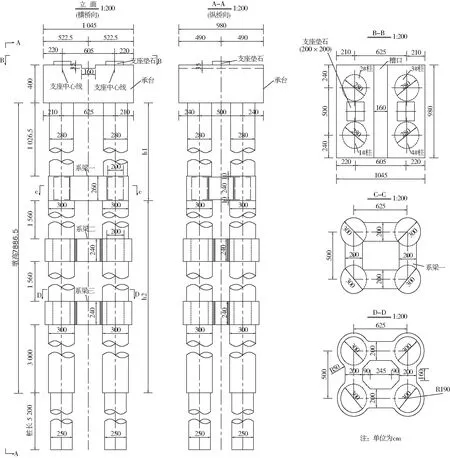
图2 4柱桩柱式框架墩构造(单位：cm)Fig.2 Structure of 4-column pile column frame pier (unit: cm)

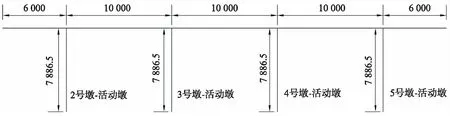
图3 缩减后5跨连续梁示意(单位：cm)Fig.3 Schematic diagram of 5-span continuous beam after span reduction(unit: cm)

1.2 有限元模型

利用有限元软件ANSYS建立桥梁-水耦合分析模型.主梁、桥墩、系梁采用实体单元Solid95，主梁参数：弹性模量Es=3.55×1010Pa，质量密度ρs=2 600 kg/m3，泊松比μ=0.2；墩柱参数：弹性模量Eh=3.00×1010Pa，密度ρh=2 440 kg/m3，泊松比μ=0.2.水体采用Fluid130单元，参考小浪底库区水文资料，水密度 1 025 kg/m3，动力粘滞系数1.05×10-3m2/s，水中声速 1 460 m/s；桥址水流速度≤4 m/s，最高水位 60 m.模型边界：不考虑崁岩桩、墩底固结，水体表面为自由液面，水体底面为刚壁界面.分析模型共计 206 776 个节点、90 752 个单元，见图4.

图4 桥梁-水耦合动力分析模型Fig.4 Bridge-water interaction dynamic analysis model

1.3 流固耦合模拟方法及验证

流固耦合效应使浸入水中的结构产生动水压力，常用计算方法有Morison方程法、辐射波浪法、流体单元法[4]和规范方法[5]等，详见表1.

表1 流固耦合方法对比

考虑本文研究目的和计算要求，选择流体单元法进行流固耦合分析.流体单元法可采用有限元软件进行数值模拟.流固耦合分析在考虑波、流水动力作用时，采用Workbench软件将Fluent流体分析与Transient Structural结构分析实现系统耦合，并进行数据交换以获得流场变化趋势及结构受力特点.Fluent模拟水流只需要将ANSYS APDL建立的模型导入，考虑流固耦合分析时，对固体区域网格局部加密以保证流固交界处网格连接顺滑，流场网格可粗糙划分以降低整体模型规模.数值波浪水槽采用Fluent多相流明渠造波法模拟.Transient Structural结构分析模块需设置Fluid Solid Interface，以便在系统耦合中与Fluent定义的流固耦合界面进行数据交换.除此之外，桥墩与主梁之间支座连接模拟是数值分析收敛的必要条件，支座连接采用Spring，应注意其刚度不能过大，否则刚体位移可能会引起计算不收敛而终止计算并报错；建模设置中如果刚度取值正常，2个连接构件之间的接触形式也可能引起整体刚度过大，例如连接采用Bonded，计算时会认为两构件之间存在刚性区域，进而产生刚性位移导致不收敛而运算停止，此时可将Bonded改为Frictionless.

为验证水流和三维波浪水槽模拟方法的可靠性，采用上述方法与文献[6]算例进行对比验证.文献[6]采用ADINA模拟水流场中的桥墩，相关参数设置为：桥墩直径为 8 m，墩高为 63 m，采用C50混凝土，混凝土弹性模量 2 760 kg/m3，泊松比0.2，墩顶质量 1 070 000 kg；水流场中水体密度为 1 025 kg/m3，动力粘滞系数1.05×10-3kg/(m·s).本文采用Workbench软件按照算例相关参数进行模拟，分析结果对比见表2和表3.

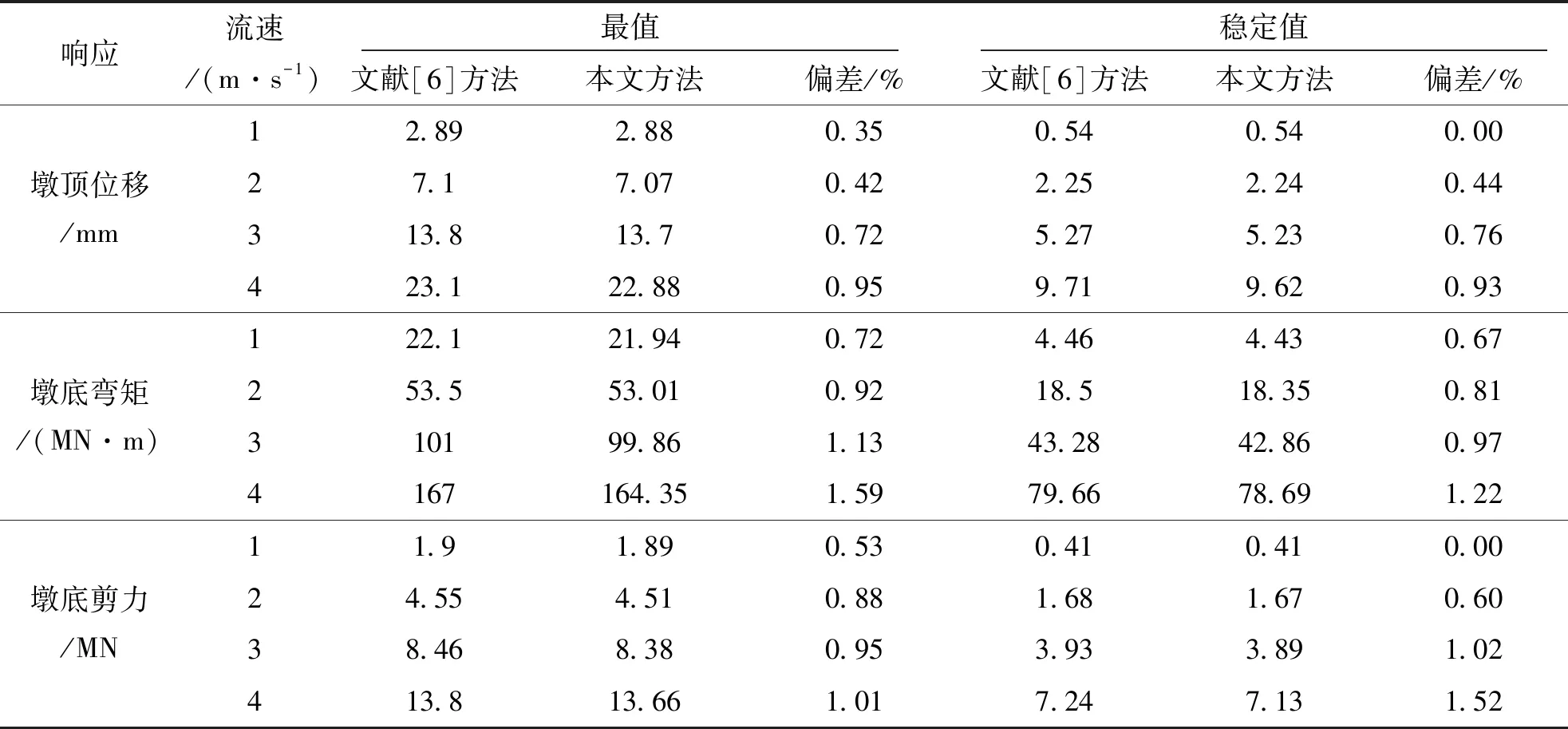
表2 水流模拟方法对比验证

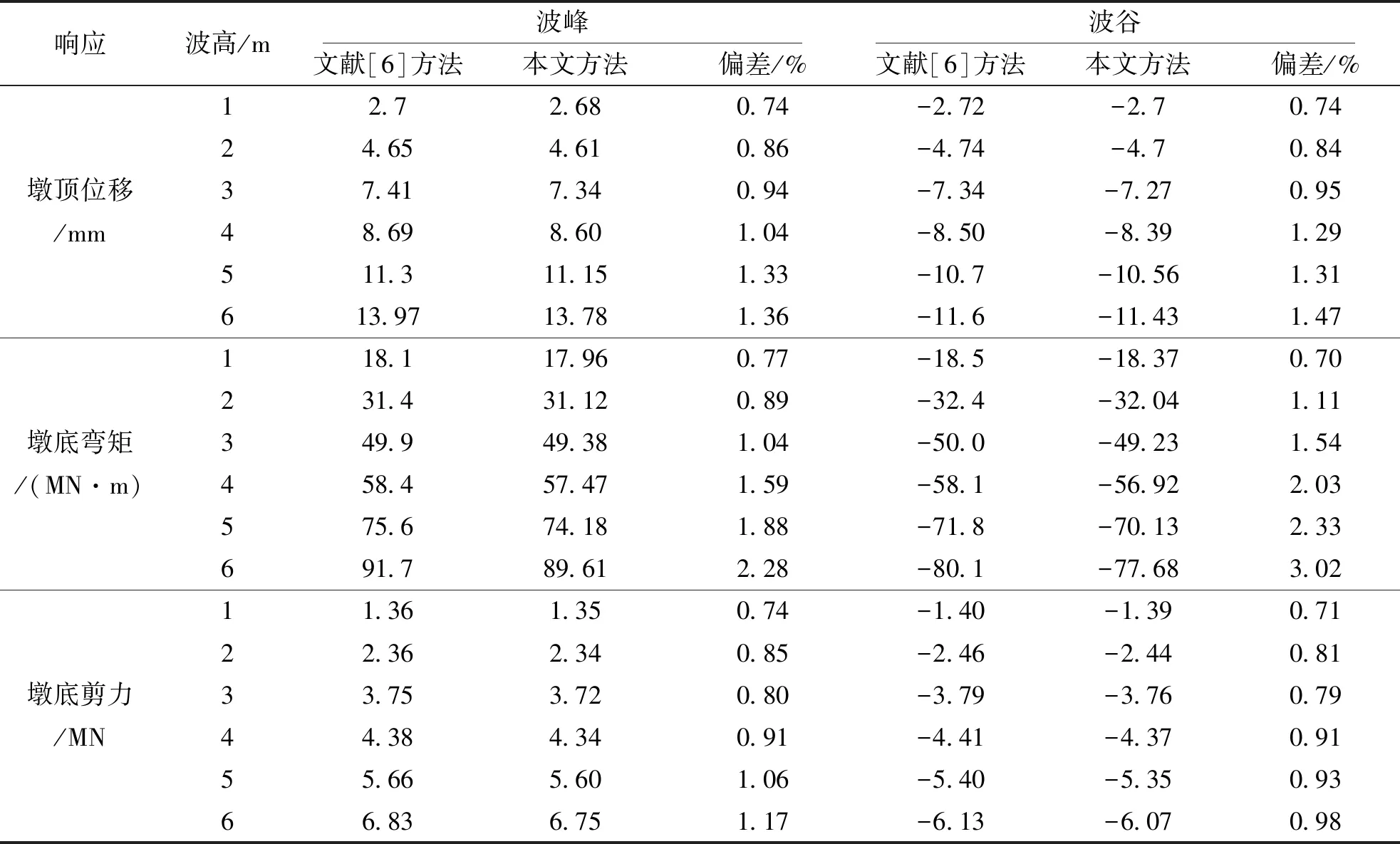
表3 波浪模拟方法对比验证

由表2和表3可知，本文所采用水流和波浪的模拟方法与文献[6]相比，动力响应最大偏差分别为1.59%、3.02%，偏差很小，表明本文的模拟方法更可靠.

2 水流、波浪联合作用桥梁结构水动力响应分析

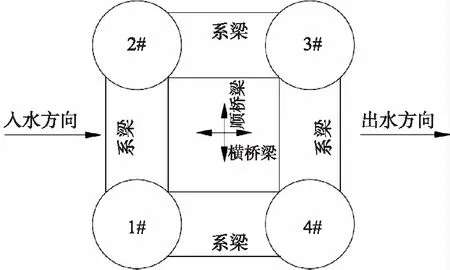
图5 墩柱编号与水流方向示意Fig.5 Numbering diagram of 4-column frame pier and flow direction

考虑到该桥位于水库库区，且桥墩形式复杂，首先对4根墩柱绕流特点进行讨论，以便确定动力响应最不利的墩柱；随后针对库区水环境，研究水流、波浪联合作用下桥梁结构的水动力响应及特点.为了方便叙述，图5给出1#柱、2#柱、3#柱和4#柱等各墩柱(墩柱编号见图2中B-B截面)与水流方向示意.

2.1 墩柱水动力效应分析

2.1.1 墩柱绕流分析

三维流场范围取200×100×Hm的长方体，H为水深.流场采用非一致网格划分，墩柱周围网格加密，各面为固定墙壁边界Wall.墩-水交界面为流固耦合界面Fluid-pier-interface.为方便叙述，4个墩柱编号为1#、2#、3#和4#(见图2的B-B截面)，水流方向如图5所示，左侧为入水方向，右侧为出水方向.当水深H=35 m(常水位)、流速u=4 m/s 时，距墩底 5 m 墩柱绕流的场速度局部矢量图见图6.

(a)桥墩绕流 (b)迎水桥墩后缘产生回流 (c)漩涡形成 (d)二次漩涡图6 墩柱绕流全过程Fig.6 Whole process of flow around pier column

圆形墩柱尾流形态与雷诺数Re有关，本文Re=1.17×107>3.6×106，故流场处于超临界状态[7]，则当水流绕流墩柱后,墩柱后端形成漩涡，即涡街现象，并且结构产生周期运动.由图6可知，1#、2#柱对水流产生阻挡，1#、2#柱和3#、4#柱之间水压力较小，但3#、4#柱有一定正压力，对水流再一次阻碍，使3#、4#柱后端先于1#、2#柱后端的压力减小，因此3#、4#柱后端先产生漩涡，但漩涡相对较小.随着水流流动，两排桥墩之间水压力变成负压，与1#、2#柱迎水面存在较大压力差，两排桥墩之间会形成较大漩涡，甚至产生二次涡流，直至漩涡消散.当流场入口处流速u=1～4 m/s、桥墩入水深度为 35 m 时，可得到不同流速对4个柱绕流影响.限于篇幅，仅给出流速 3 m/s 时距墩底 25 m 处截面的速度场和压力场，见图7.

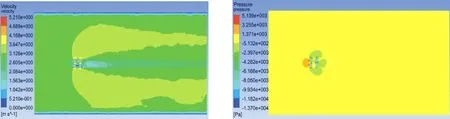
(a)速度场 (b)压力场图7 流速 3 m/s 各柱绕流速度场和压力场Fig.7 Velocity field and pressure field around each column at the velocity of 3 m/s

由图7可知，流场的速度分布接近对称，且墩柱两侧速度明显增大，而墩柱后侧水流速度逐渐减小，甚至出现回流现象.分析还显示墩柱后缘尾流速度随着流速变化越来越明显，1#、4#柱速度差异比2#、3#柱速度差异更显著，各柱之间相互干扰使得速度场和压力场不对称，这也预示4个柱水动力响应不同.

2.1.2 各墩柱水动力响应对比分析

2.1.1节预示4柱的水动力响应不同，限于篇幅，仅给出水深 35 m 时不同流速对柱底剪力响应影响，见表4.

表4 水深35 m时不同流速各墩柱剪力响应最值和稳定值

由表4可知，各墩柱剪力响应随水流速度增大而增加.由于水流冲击作用，桥墩产生绕流，相比其它3个墩柱，2#柱后端回流产生负动水压力大，与墩柱前端水流冲击正向动水压力抵消，2#柱动力响应最值和稳定值均最小.定义各墩柱间扰动系数为式(1)：

R=Qi/Qave

(1)

式中：i为墩柱编号；Qi为墩柱响应；Qave为墩柱平均响应.扰动系数R越小则墩柱所受干扰越明显.图8为不同流速各墩柱之间剪力响应最值和稳定值的扰动系数R.

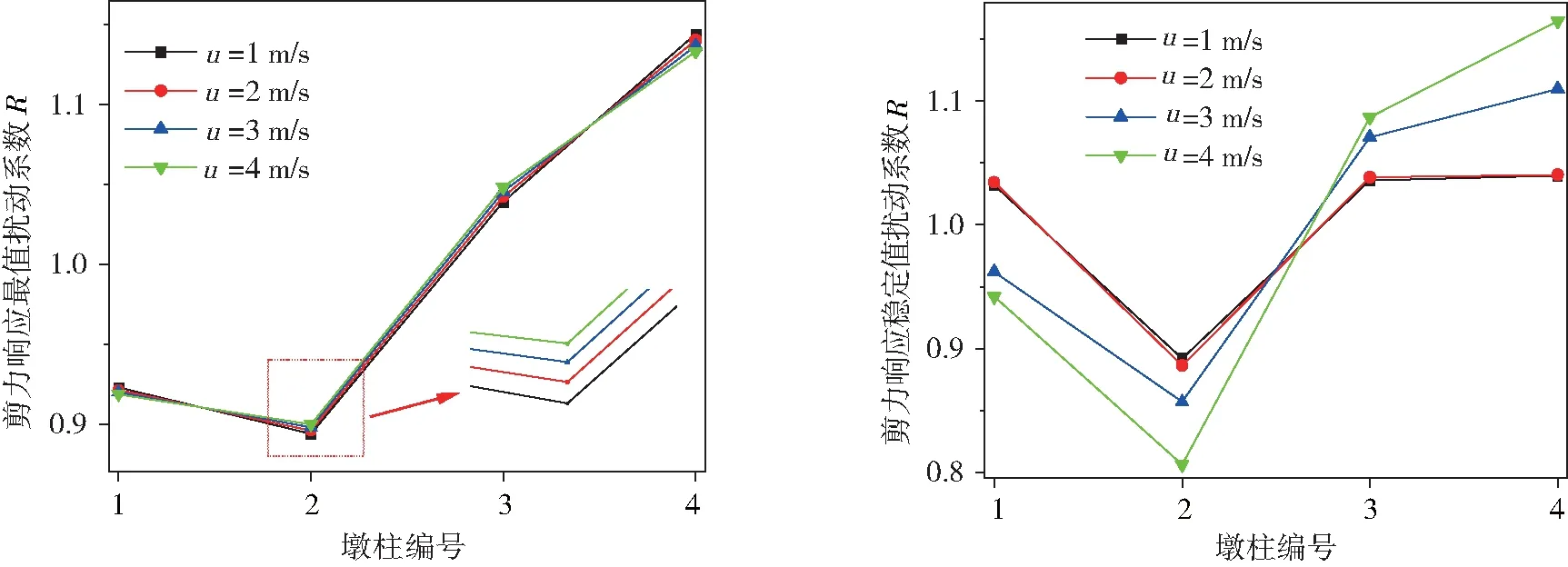
图8 不同流速各墩柱剪力响应扰动系数RFig.8 Disturbance coefficient R of shear response of each pier column at different flow velocities

由表4及图8可知，各墩柱动力响应并不相同，无论是最值响应，还是稳定值响应，2#扰动系数R最小，表明4根墩柱水动力响应不同，且2#受到其它3个墩柱干扰最明显.

2.2 水流、波浪联合作用的水动力响应

不论是水流、波浪联合作用的水动力响应，还是地震作用的动力响应，均以墩顶变形和墩底内力为表征指标，此外为了避免水槽边界对数值分析结果的影响，后续动力响应均取自桥梁中间3号墩(见图3).为了分析水流对波浪场影响，令水流影响系数IF=(波、流共同作用响应最值-波浪单独作用响应最值)/波浪单独作用动力响应最值×100%.限于篇幅，仅以不同流速3号墩动力响应最值为例，见表5.其中波浪和水流指仅考虑其单独作用，波、流为波浪和水流共同作用.图9为水流影响系数.

由表5和图9可知，流速使动力响应增大；波、流联合作用时桥墩动力响应最值不是波浪或水流单独作用动力响应叠加.波、流联合作用时，桥墩动力响应在波峰处达到最大值，在波谷处达到最小值；水流影响系数IF最大为12.96%，表明波浪在动力响应中起主导作用.

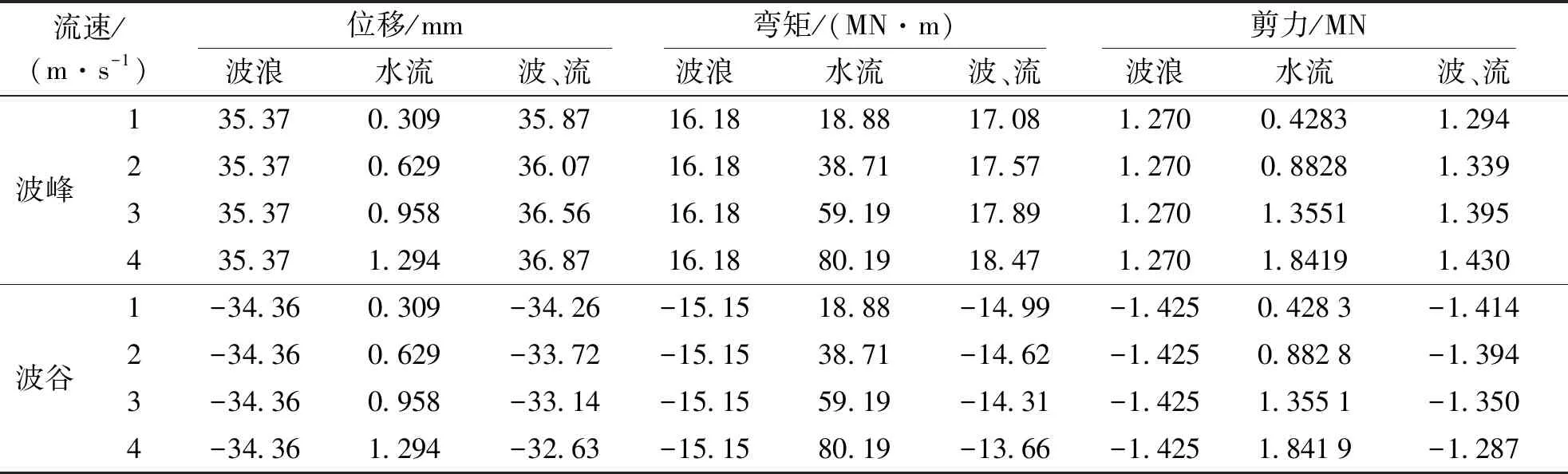
表5 不同流速桥梁3号墩动力响应最值

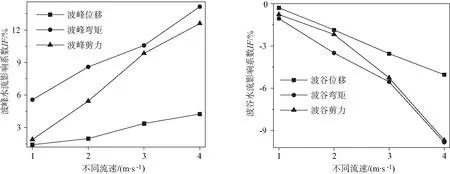
(a)波峰作用 (b)波谷作用图9 不同流速作用水流影响系数Fig.9 Influence coefficient of flow under different velocities

3 库区桥梁地震响应分析

3.1 自振特性分析

为了讨论桥梁结构地震响应，首先应分析结构自振特性.考虑最大水深 60 m，研究不同水深时结构自振特性.表6为桥梁前5阶频率和振型.

由表6可知，桥梁自振频率随水深增加逐渐降低,这表明随着水深增加，水体对桥梁自振扰动干扰越明显，桥梁对应各阶频率变小;在水深小于 10 m 时，桥梁自振频率变化很小，且1阶纵飘频率变化很小；桥梁前3阶侧弯频率变化较明显.

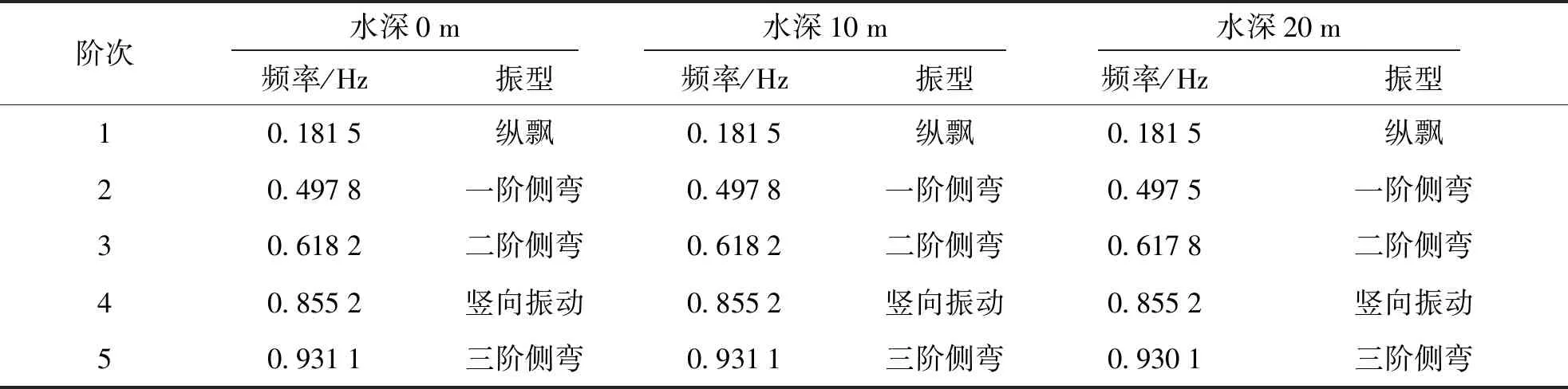
表6 不同水深桥梁前5阶自振特性

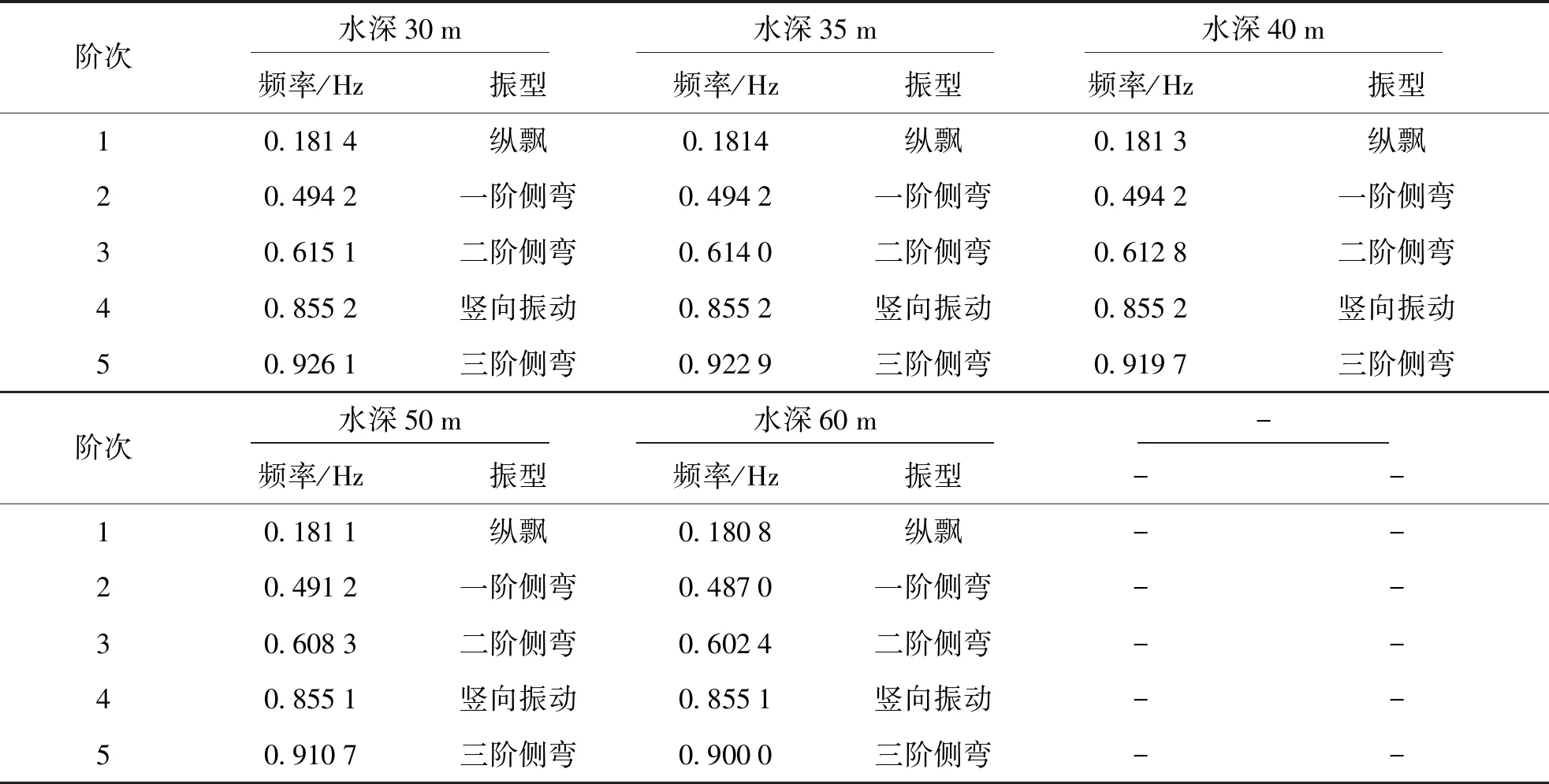
续表6

3.2 无水和静水时桥梁的地震响应

为保证所选地震波的合理性，应按照以下原则：(1)场地条件相同:依托桥梁场地类别为II类场地；(2)地震波反应谱与场地卓越周期接近:场地特征周期为 0.40 s；(3)设防烈度相同：本桥抗震设防类别为B类，抗震设防烈度8度.基于以上原则选择El-Centro波进行地震响应分析，El-Centro波适合II类场地，其卓越周期为 0.38 s,并对其进行峰值调幅以满足设防烈度要求.

考虑到水流方向垂直于桥跨，仅取符合桥址场地条件的El-Centro地震波对大桥进行横桥向一致激励.为了确保结构抗震安全，应由最不利地震响应控制设计，故后续分析内力取3号墩的最值地震响应某根柱底(墩柱编号见图2的B-B截面)，位移取3号墩的墩顶.限于篇幅，表7仅给出无水及 35 m 水深静水时3号墩各墩柱的内力及位移.

由表7可以看出，2#墩柱内力相对较大，图10为无水和水深 35 m 静水时2#墩柱底最大弯矩和墩顶位移时程曲线.

由表7和图10可知，各个柱的墩底弯矩和墩底剪力各不相同，2#柱内力响应最大，但由于桥墩设置有3道系梁，各柱底的弯矩和剪力最值响应差别不大.静水工况地震响应大于无水工况地震响应，表明水会放大结构地震响应.

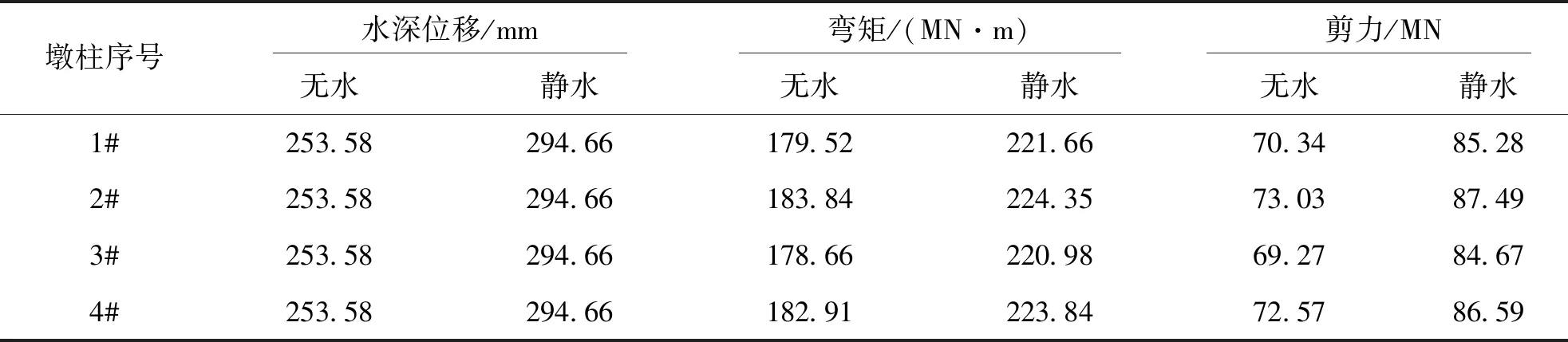
表7 El-Centro波横桥向一致激励作用各墩柱地震响应最值

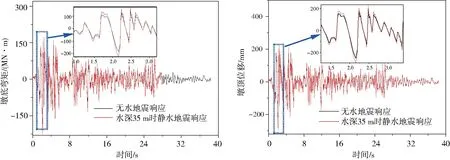
图10 墩底弯矩、墩顶位移时程曲线Fig.10 Time history curve of pier bottom bending moment and pier top displacement

3.3 考虑波浪、水流共同作用桥梁地震响应

取流速u=2 m/s，波浪高度 2 m，水深35米，表8为考虑波、流作用地震响应最值.

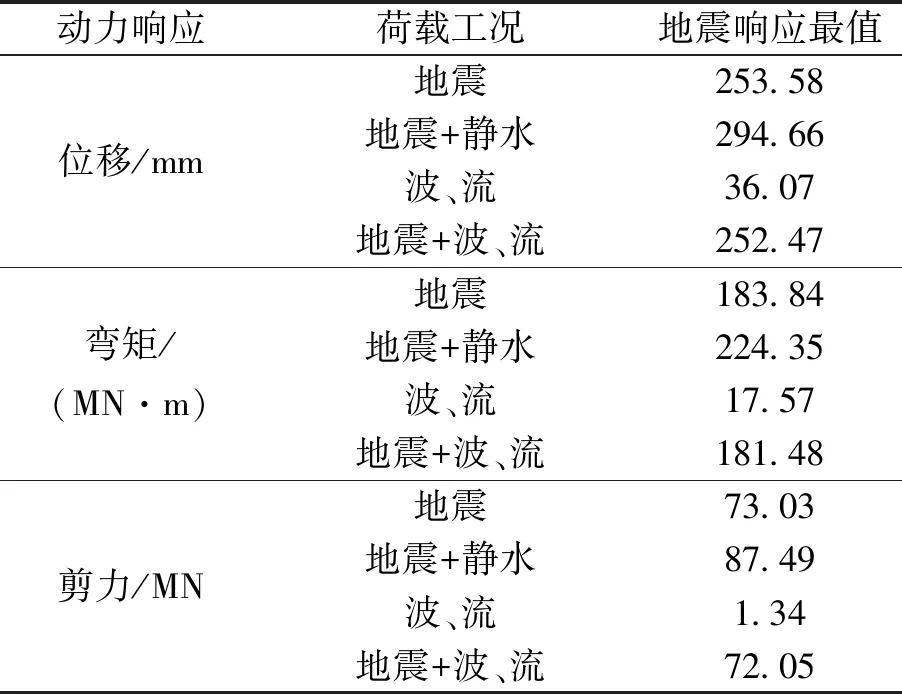
表8 考虑波、流影响El-Centro波横桥向一致激励地震响应最值对比

由表8可看出，静水时地震响应最值始终最大，这是由于静水环境地震作用除了使结构自身产生地震响应外，还会引起水体运动，而水体运动又会对结构产生动力作用，进而使结构的动力响应增加.波、流共同作用时地震响应并不是各种作用单独作用动力响应叠加.波、流环境的地震响应小于静水时地震响应，故波、流环境削弱了结构地震响应.文献[6]考虑波、流环境分析远、近场深水桥梁地震响应，得出“波、流环境对桥梁地震响应可能增强，也可能削弱”的结论，本文进一步的分析亦有类似结论.因此，波、流环境对桥梁地震响应的影响与地震波、激励方式等因素有关，应根据具体情况进行更多工况动力响应分析，以便获得设计控制值.

3.4 波高、水深对库区桥梁地震响应影响分析

为了讨论波高、水深对地震响应影响，表9和表10给出不同波高、水深时3号墩墩底弯矩地震响应最值.

由表9和表10可知，静水环境地震响应最大，考虑波、流环境的地震响应最值均小于地震单独作用下的响应最值；随着水深增加，地震+波、流的动力响应逐渐减小，且响应最值不是地震单独作用于波、流作用的动力响应最值的叠加；波、流作用削弱结构地震响应，且随着水深、波高增加，地震响应削弱越明显.

表9 水深对库区桥梁弯矩响应最值影响(流速u=2 m/s，波高 2 m)

表10 波高对库区桥梁弯矩响应最值影响(流速u=2 m/s，水深35 m)

4 结 论

针对无水、静水以及波、流联合作用对库区复杂桥墩连续梁动力响应的影响，以缩跨后跨黄河小浪底库区某4柱桩柱式框架墩连续梁为例，考虑流固耦合效应，研究了4柱桥墩在水流作用下绕流及波、流联合作用动力响应，并详细分析波浪、水流和水深对结构地震响应的影响.通过分析得出以下结论：

1)绕流分析显示4个柱速度场和压力场不对称；4根墩柱水动力响应不同，2#受到其它3个墩柱干扰最明显.

2)波、流联合作用时，桥墩动力响应随着流速增加而增加，波浪在动力响应中起主导作用，且波、流联合作用水动力响应并非两者单独作用叠加.

3)对于依托桥梁及本文所分析工况，与无水工况相比，静水工况的地震响应更大，静水使结构变形和内力响应增大；波、流环境时地震响应不是地震和波、流的单独作用叠加；波、流环境削弱了地震响应，且随着水深和波高增加，地震+波、流的动力响应削弱越显著.

4)波、流环境对桥梁地震响应的影响与地震波、激励方式等因素有关，应根据具体情况进行更多工况动力响应分析，以便获得设计控制值.