考虑交通安全的交叉口信号相位与配时综合优化模型

成 卫，黄金涛，陈昱光，郭晋成，徐红彬

(昆明理工大学 交通工程学院，云南 昆明 650500)

0 引 言

我国城市交通事故约有30%发生在交叉口[1]，而传统的信号相位方案设计和配时优化通常只考虑了交叉口的通行效率，忽略了交叉口的通行安全问题.如何将交叉口的安全特性嵌入到相位设计与配时优化中，对改善交叉口通行安全具有重要意义.目前,交叉口的相位设计分为2种:一种是凭借对交叉口的定性分析和实践经验进行相位设计，这种方法多根据主观经验，缺少精确的数学表达；另一种是使用聚类或集合的方法根据交叉口的车道功能、交通流量以及车辆轨迹进行定量分析建立数学模型[2-4]，这种方法过于简单，无法适用小型交叉口的简单相位，且只考虑了交叉口的通行效率忽略了交通安全影响.对于信号配时参数的优化，许多学者多以交叉口某一单个评价指标如车均延误、停车次数、排队长度以及交叉口的通行能力等作为优化目标进行信号配时[5]，但单个目标优化效果远远达不到预期，通常是解决了某个问题又带来了新的问题.为了弥补单个目标的缺陷,一些学者又选取了多个优化目标进行研究[6-8]，但这种方法通常只针对机动车通行参数优化，忽略了行人和非机动车.考虑到信号配时的优化效果与信号相位设置存在密切关系，Shen等[9]改进了传统 K-medoids算法，基于饱和度和绿信比数据建立相位组合模型，并通过双层规划模型优化信号配时，提高交叉口的通行能力；卢凯等[10]提出了多轮同步优化模型，通过计算各相位的分配时间兼顾了行人过街需求，以车流的通行需求满足度作为优选指标进行信号相位与配时同步优化；刘邓[11]以平均延误最小为目标，建立了单点交叉口相位设计与配时组合优化模型.

上述研究主要关注的是机动车延误的降低与通行能力的提高，忽略了行人与非机动车作为重要交通参与者的通行权力，甚至忽略了右转机动车对信号交叉口配时优化的影响.这种设计理念通常难以满足机动车、非机动车与行人的通行需求，使得交叉口信号控制方案难以取得较好效果，无法达到全局最优.基于上述问题，本研究建立了基于交叉口通行成本最低的交叉口相位与配时综合优化模型.该模型提高交叉口通行效率的同时，考虑了交叉口各类交通流的安全问题，特别是可以保障行人与非机动车安全、快速地出行.

1 模型建立

1.1 机动车与行人延误模型

交叉口的延误主要是由机动车延误、行人延误以及非机动车延误组成.因为非机动车通常伴随行人通过交叉口，因此可将非机动车流量换算为行人流量.根据已有研究[12]，非机动车转换成行人的换算系数为2.0，进而可将非机动车延误转换为行人延误.

1.1.1 机动车延误模型

机动车延误主要包括控制延误、机动车转弯时与行人的冲突延误.信号交叉口机动车控制延误采用HCM2010中的延误估计模型，交叉口控制延误为：

(1)

式中：dv为机动车控制延误，s；C为信号周期长度，s；x为饱和度；u为绿信比；PF为均匀信号联动修正系数；T为观测分析时长，h；K为信控方式校正参数；I为车辆到达校正参数.

机动车转弯时与行人的冲突延误主要是由于机动车需要避让行人而减速.根据文献[13],行人与机动车冲突延误为：

(2)

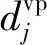
交叉口机动车总延误为：

(3)

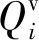
1.1.2 行人延误模型

行人延误包括行人等待红灯的信号延误，同时也包括了转弯机动车与行人之间形成的冲突延误.延误表达式如下：

(4)

(5)

(6)

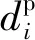
1.2 交叉口冲突分析

交通冲突是不同道路使用者在同一时间需要占用同一道路资源形成的，交通量的多少直接影响着交通冲突数量的大小.为了研究交通量与交通冲突数之间的关系，基于昆明市新迎路—文艺路与西昌路—安康路两交叉口24小时的视频数据，分别建立人—车冲突模型与车—车冲突模型.

1.2.1 信号交叉口人-车冲突模型

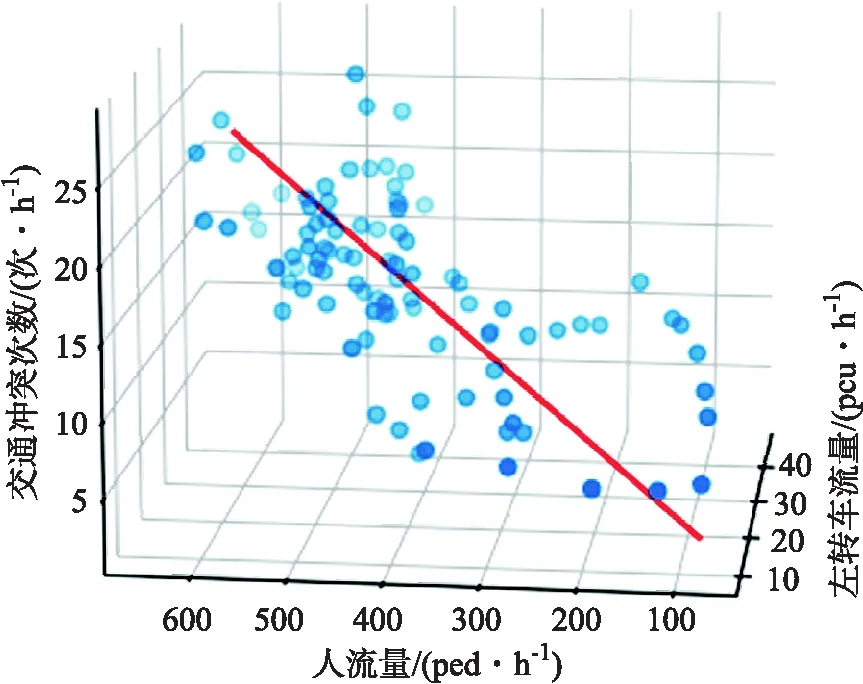
图1 左转机动车与行人冲突 Fig.1 Left turn vehicle conflict with pedestrians

(7)

(8)

表1 左转机动车与行人冲突模型参数检验表

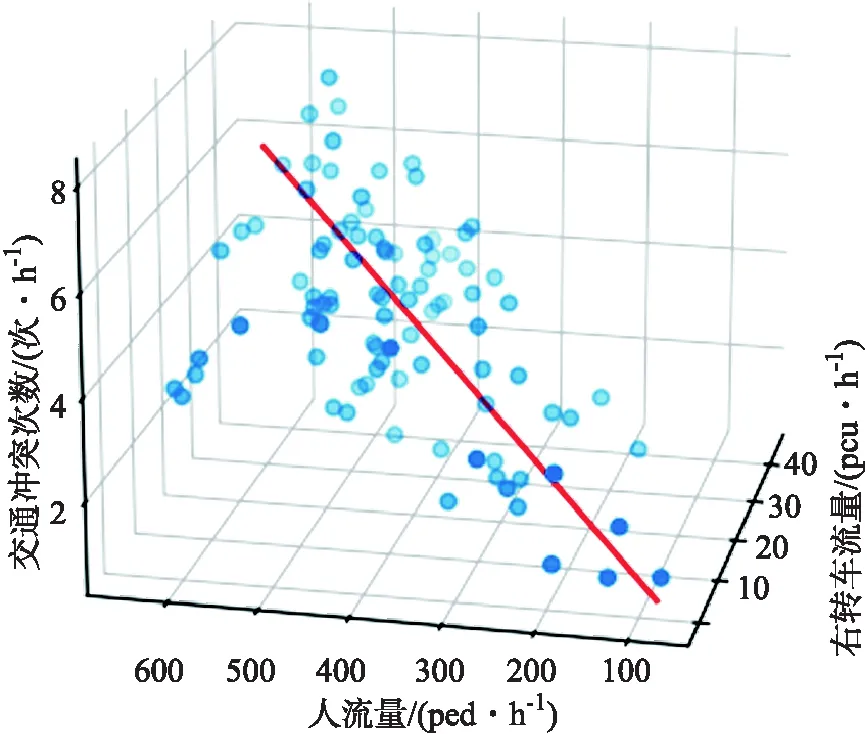
图2 右转机动车与行人冲突 Fig.2 Right turn vehicle conflict with pedestrians

对式中各项参数进行检验，如表2所示，右转车流量的显著程度为0.027，行人的显著程度为0，表明可以根据该模型预估右转机动车与行人形成的冲突数.

1.2.2 信号交叉口车-车冲突模型

(9)

表2 右转机动车与行人冲突模型参数检验表

图3 左转机动车与直行机动车冲突Fig.3 Conflict between left turning vehicle and straight driving

对式中各项参数进行检验，如表3所示，左转车流量的显著程度为0.073，直行车流量的显著程度为0，表明可以根据该模型预估直行机动车与左转机动车形成的冲突数.

1.3 交叉口通行成本模型

交叉口行驶安全通常根据交叉口事故数进行评价，但事故的偶然性使其难以预测，往往是在交叉口发生事故后才对交叉口进行整治改善.为了在设计之初就统一交叉口运行效率与交叉口安全之间的关系，通过将交叉口延误与交叉口安全转换成对应的成本，建立交叉口通行成本模型：

M=MD+MS

(10)

式中：MD为交叉口延误成本，元/h；MS为交叉口安全成本，元/h.

1.3.1 交叉口的延误成本

交叉口的延误成本主要包括机动车延误成本与行人及非机动车延误成本：

MD=mvDv+mpDp

(11)

式中：mv为机动车延误单位成本，mp为行人延误单位成本.通过对出行者时间价值的计算[14]，mp为21.816元/h；机动车按平均承载率1.24人/辆计算，则mv为27.036元/h.

1.3.2 交叉口的安全成本

交叉口的安全成本指交叉口发生事故所造成的损失成本.由于交叉口的交通冲突与交通事故存在线性关系[15]，因此可由事故成本预估交叉口单位冲突成本，交叉口的冲突成本ms为：

ms=K1(m1h1+m2h2+m3)

(12)

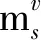
(13)

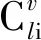
1.4 交叉口相位设计与配时综合优化模型

将交叉口东西向和南北向分为两个部分，各包含了7个基本相位(p1～p7)，分别为：p1对称放行相位(左转与直行分离)；p2对称放行(左转与直行不分离)；p3单口放行相位，p4搭接对称直行的单口放行相位；p5搭接对称左转的单口放行相位；p6搭接某一进口的搭接相位(东进口、北进口)；p7搭接另一进口的搭接相位(西进口、南进口).以南北向为例，基本相位如图4所示.对于行人相位，考虑到转弯机动车对它的影响，其一般伴随直行机动车一同放行，而右转机动车只与行人与非机动车发生冲突而不与其他机动车发生冲突，因此右转机动车存在2种状态：第一种是行人与非机动车流量少，给右转机动车留下足够的可穿越间隙，此时右转机动车可直接与行人和非机动车叠加同时放行；第二种是行人与非机动车流量较大,右转机动车无法穿越，此时右转机动车需与行人和非机动车相位分离.右转机动车的绿灯时长可表示为：

(14)

交叉口的车道功能设置与交叉口信号相位设计有着密切关系.当交叉口某一进口不存在左转与直行专用车道,则对应的整个方向上均不能设置搭接相位;当缺少右转专用车道时，该进口右转机动车只能伴随直行车通过交叉口.根据交叉口各进口车道功能限制确定东西方向与南北方向的基础相位，再两两组合确定交叉口的相位方案集合P(x).根据通行成本基础模型，建立如下相位设计方案和配时优化综合优化模型：

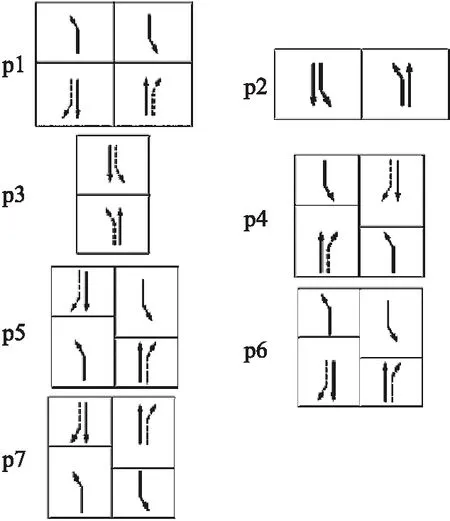
图4 南北向基本相位Fig.4 North-South basic phase

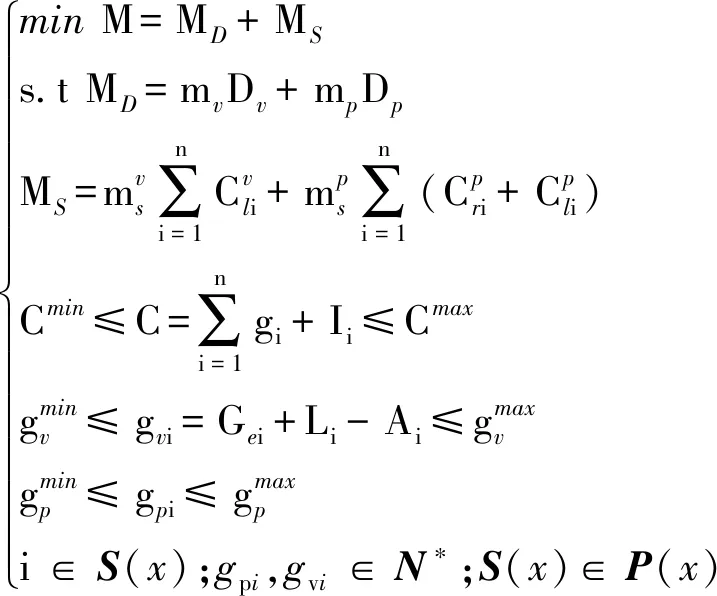
(15)

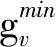
1.5 模型优化流程

上述模型为整数非线性规划.考虑到交叉口的相位方案不多且周期参数阈值有限，因此使用python实现该模型算法，对模型参数进行求解，最终直接输出交叉口相位方案,其优化流程如图5所示.

2 案例分析

2.1 交叉口情况

选取玉溪市玉兴路—棋阳路交叉口作为案例，使用VISSIM构建交叉口仿真模型.该交叉口各进口均为四车道，出口均为两车道，各方向均设置了非机动车道，现状渠化设计如图6所示.交叉口信号相位南北方向为对称放行，东西方向为单口放行，右转机动车不受控制，周期时长为 160 s，交叉口相位方案如图7所示.交叉口早高峰流量如表4所示.

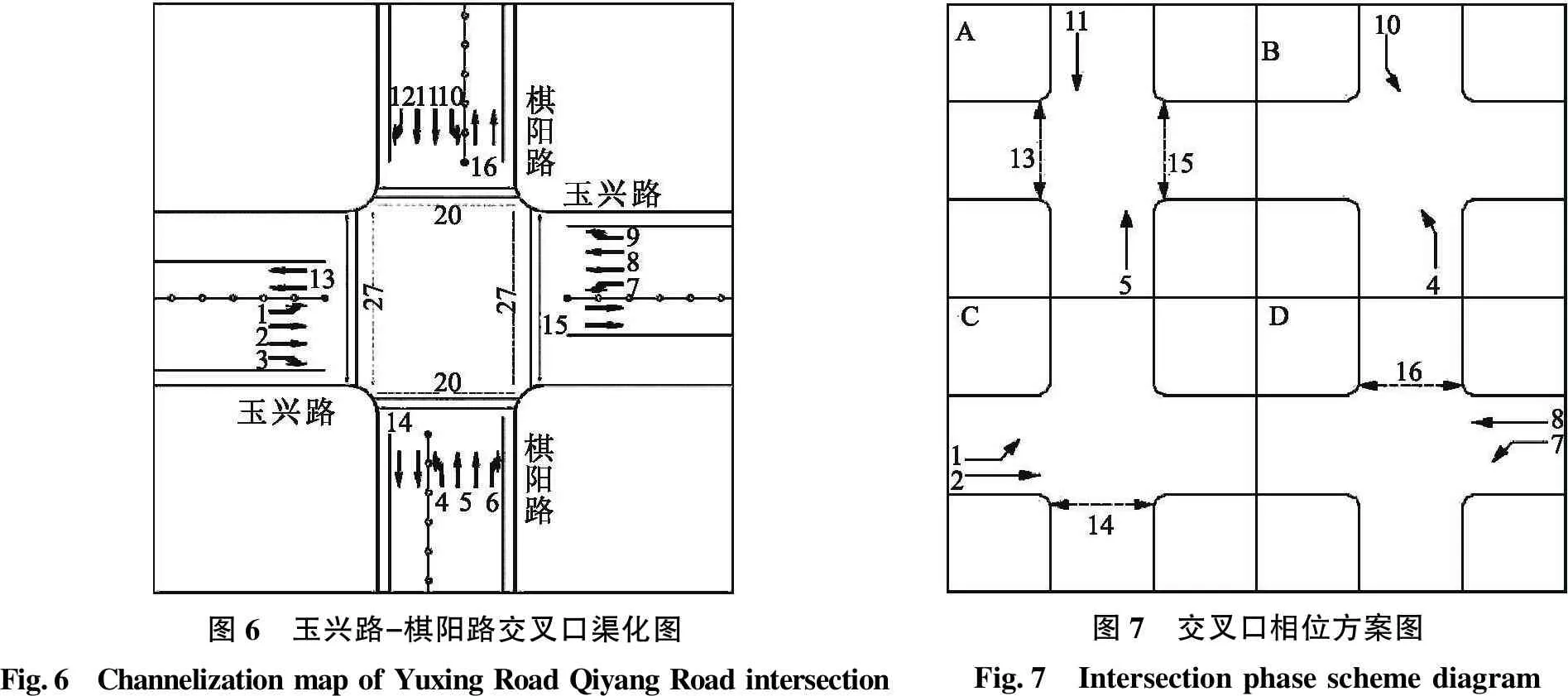
图6 玉兴路-棋阳路交叉口渠化图Fig.6 Channelization map of Yuxing Road Qiyang Road intersection图7 交叉口相位方案图Fig.7 Intersection phase scheme diagram

表4 交叉口交通流量

2.2 相位与配时的数值优化

将该交叉口的基础信息使用python语言输入到程序中，根据交叉口车道功能，确定7个基本相位(数字表示交通流编号).由于交叉口各相位绿灯时间由流量比分配而来，该实例交叉口的东西向的搭接相位p4和p6，南北方向的搭接相位p5和p7无法满足搭接的相位与流量比相匹配的约束，给予取消，因此南北方向与东西方向两两组合后的相位集合P(x)包含了25种相位方案.在各相位方案中枚举该方案下不同的周期时间和行人过街时间以及右转机动车的过街方式，通过不断的迭代直到得到最终的相位及配时优化方案.

根据综合模型优化，其对应的相位方案的周期迭代图和相位方案如图8所示，其周期时长为 134 s.为了仿真验证对比该优化方案，继续使用该模型优化交叉口，所不同的是该优化方案只考虑交叉口通行效率不考虑交叉口的安全因素，即以交叉口的延误成本最小为目标，继续使用上述迭代过程.优化后的交叉口相位方案的周期迭代图和相位方案如图9所示，周期时长为 124 s.

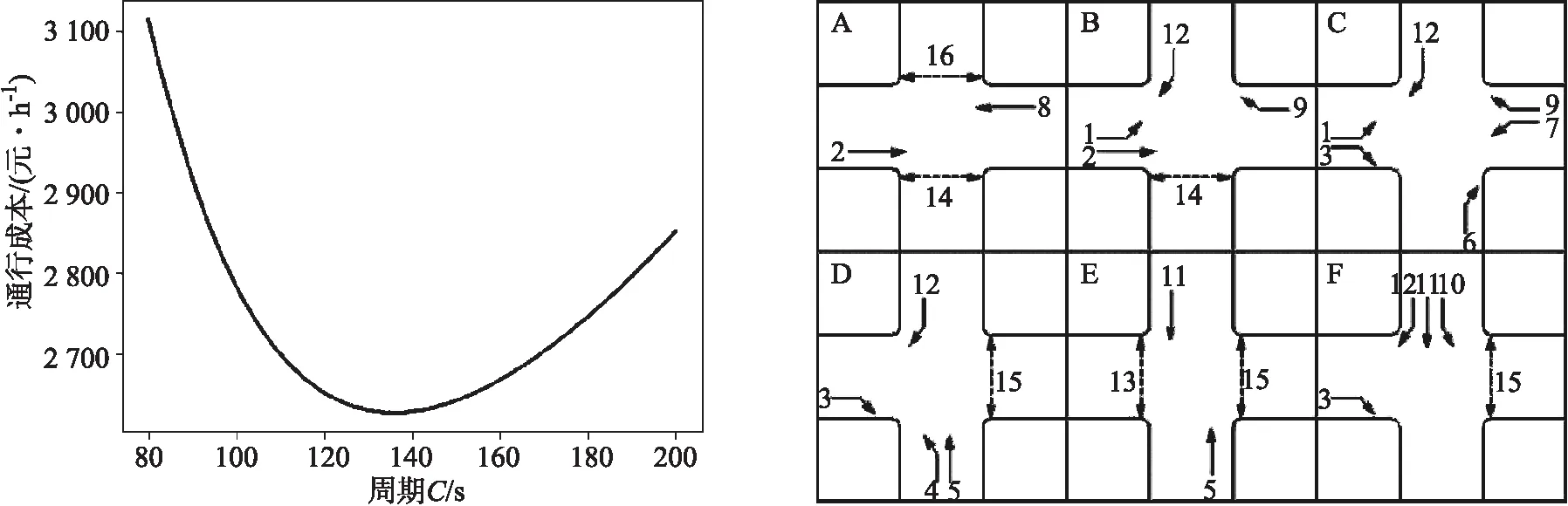
(a)周期迭代图 (b)相位图图8 综合优化方案Fig.8 Integrated optimization solution

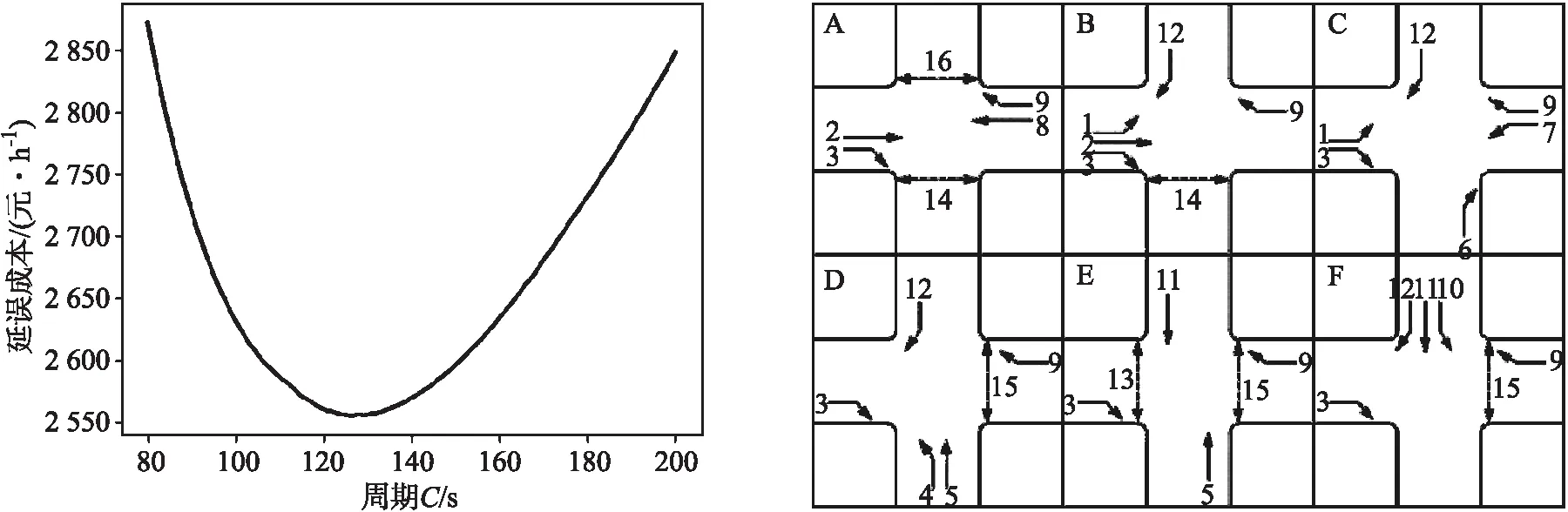
图9 最小延误方案Fig.9 Minimum delay program

原始方案、综合优化方案和最小延误方案的程序运行结果如表5所示.由表5可知，原方案的周期时间长但其延误成本最高，表明单纯地追求放行时长并不会降低交叉口延误；综合优化方案中的延误成本比最小延误方案中的延误成本要高，但对比两方案的通行成本大小，由于最小延误方案牺牲了交叉口行人和机动车的通行安全，最小延误方案比综合优化方案要高4.6%，这与当前使用的大多数的相位优化方法相似.

表5 程序运行结果

2.3 3种方案仿真对比分析

使用VISSIM仿真软件对上述3个方案进行仿真对比，结果如图10所示.通过图10可以看出，最小延误方案比综合优化方案的车均延误减少了13.7%，这是由于综合优化方案中右转机动车均受控，尤其是东进口右转和西进口右转，导致综合优化方案中整体的交叉口车均延误比最小延误方案大；由于原方案周期时间过长且原方案行人和右转机动车存在冲突延误，因此综合优化方案相对于原方案车均延误降低了2.6%，行人平均延误降低了14.9%.

使用python进行数值仿真验证3种方案的安全特性，结果如图10(b)所示.受信号控制的影响，3种控制方案的主要安全影响来自于机动车与行人的冲突.可以看出，综合优化方案的冲突数明显小于其他2种方案，整体冲突数比原方案下降了82%，比最小延误方案下降了77%，极大减少了行人与车辆之间的冲突，降低了交叉口内的安全隐患，使得交叉口的整体通行环境得到改善.

3 总 结

1)本研究以最小通行成本为目标，完成了对交叉口信号相位的优选，通过使用延误成本约束和安全成本约束使得所选交叉口控制相位方案满足交叉口通行效率的同时，保障了交叉口的通行安全.

2)本研究建立的相位配时优化模型能够适用于大多数的交叉口信号相位设计，特别是将行人和非机动车整合到模型内，保障了行人和非机动车的通行需求.另外，该模型还考虑了交叉口车与人之间的冲突和车与车之间的冲突，从信号相位配时入手，极大减少交叉口的冲突点，继而减少事故隐患.

3)根据实例分析，验证了该模型的有效性，使用该模型优化交叉口能够较好地权衡交叉口的通行安全和通行效率之间的关系，让交叉口的信号相位设计更加的科学与规范.

4)该相位配时优化模型只是将行人简单的和直行机动车归于同一相位，忽略了在畸形交叉口中行人与非机动车相位的设计问题，因此后续的研究可着重于行人和非机动车在复杂交叉口环境下其信号相位的设计与配时.