碳排放强度对长江经济带绿色发展水平的空间溢出效应研究
胡孟颖 ,刘德志,b,胡雅洁
(1.安徽财经大学a.统计与应用数学学院;b.数量经济研究中心,安徽 蚌埠 233000;2.滁州学院 经济与管理学院,安徽 滁州 239000)
0 引言
“十四五”规划提出加快推进绿色低碳发展,既要推动经济增长,也要改善环境质量,要全面高效地利用资源,避免不必要的浪费.习近平总书记在中央财经委员会第九次会议中强调,“十四五”是碳达峰的关键期、窗口期,因此需要在发展的过程中加大绿色技术创新力度,合理安全地推动清洁低碳能源使用,力求能够按期实现碳达峰、碳中和的目标.
深入打好污染防治攻坚战,需要提升环保意识,促进绿色低碳循环发展.本文以长江经济带各区域为研究对象,研究样本期间碳排放强度与绿色发展水平之间的关系,并将环境规制、创新投入等变量纳入研究框架,分析其影响效应.本文研究结果可为长江经济带构建绿色低碳安全高效的能源体系和制定科学的经济环保政策提供参考.
1 文献综述
1.1 绿色发展水平测算及影响因素研究
有关绿色发展水平的测算和绿色发展水平的影响因素研究成果较多,李光勤等[1]以黄河流域为样本,运用全局Malmquist-Luenberger 指数测得2001—2018 年的绿色全要素生产率来表征绿色发展水平,分析绿色发展水平时空演变特征;李雪松等[2]以研发驱动理论作指导,构建DEASBM 模型,对传统型、创新型绿色发展效率分别进行了测算,并分析了其在各区域的分布特征以及FDI、城镇化水平等变量对其的影响效应;郝淑双等[3]从资源利用、环境质量、绿色生活等维度出发构建评价体系,用加权平均法测算出绿色发展指数,进而构建SDM模型,分析技术进步、环境规制等对绿色发展水平的影响.基于上述研究,本文选取包含非期望产出的DEA-SBM 模型测算长江经济带11省市的绿色发展水平.
1.2 碳排放强度研究
在碳强度研究方面,王锋等[4]基于Divisia指数分解法,分析了全国各省市及其他变量对全国碳强度下降的影响,结果发现,辽宁、黑龙江、河北等省市的贡献最大,海南、宁夏等省市则阻碍了全国碳强度的下降,且每个省份的碳强度、能源强度等的变动共同影响全国碳强度变化;张伟等[5]在对碳排放量进行因素分解的基础上,测度了碳排放强度并进行了影响因素分析,结果表明,各产业的碳排放强度都是在不断下降的,并且产业体系能源碳排放效率、能源结构等都对碳排放强度产生了影响;史丹等[6]从制造业产业结构优化角度出发,分析了产业结构优化调整目标以及节能减排的潜能,认为产业结构优化调整可以降低碳强度的水平,为实现“经济增长和环境保护”双赢提供可能.本文则选取IPCC 推荐的碳排放计算公式计算出各省市二氧化碳排放量,并以碳排放量与地区GDP的比值来表示碳强度.
1.3 碳强度与绿色发展水平间关系研究
关于碳强度与绿色发展水平之间的关系,高赢[7]运用US -SBM 模型测算了样本区域的绿色发展绩效,并对其影响因素进行了分析,结果发现,碳强度对各区域的绿色发展绩效提高作用十分有限,节能减排仍有较大的空间与潜力;陈瑶等[8]从技术和创新双视角出发,探究工业绿色发展与工业碳强度间的关系,结果表明,工业碳强度随着工业绿色发展呈倒“U”型趋势,也就是说在绿色发展水平不断提高时碳强度会先上升再下降.也有文献也将绿色发展与低碳发展纳入同一体系进行测度分析,张友国等[9]从发展动力、生活系统等角度出发,构建了绿色低碳循环发展经济体系,将低碳、绿色、循环发展纳入一个体系中进行分析,并用时空极差熵权法进行测度,结果表明样本期间该指数在全国范围内都有所提升;赵慧卿等[10]构建了绿色低碳循环发展经济指标体系,并结合双重激励模型与最小方差法进行动态综合评价,结果表明,全国范围内的绿色低碳循环发展是不均衡的,并且受长边原则支配,需要加强对长边的提升.
本文在借鉴上述研究成果的基础上,对碳排放强度与绿色发展水平之间的空间关系进行了研究,并尝试在以下方面进行扩展:(1)考虑到碳强度对绿色发展水平的非线性影响,将碳强度的二次方项纳入模型中;(2)在进行空间计量分析时,列出SDM 模型、SEM 模型和SLM 模型的回归结果,以对比分析结果的稳健性.
2 模型设计与变量选取
2.1 空间计量模型的建立
为了研究碳排放强度对绿色发展水平的影响,选取绿色发展水平(GDL)作为被解释变量、碳排放强度(EI)作为解释变量,由于碳排放强度与绿色发展水平之间可能存在非线性关系,拟在模型中引入碳排放强度的平方项.相关文献表明,环境规制(ER)、人均国内总产值(PGDP)、产业结构(IS)、进出口(IE)、R&D 人员(RDFE)、R&D 经费支出(RDIE)和专利申请授权数(DPA)也会对绿色发展水平产生重要影响,故将这些变量作为控制变量X,构建如下计量模型:

其中,i,t,εit分别为省市、年份、随机扰动项.
考虑到绿色发展水平与碳排放强度的空间滞后项对绿色发展水平的影响,建立空间杜宾模型如下:

其中,ωij为空间权重矩阵,σ为空间自回归系数,φi为空间效应,τt为时间效应,εit为随机误差.
2.2 变量测度与数据来源
本文选取了长江经济带2009—2019 年11 个省市地区的面板数据,数据主要来源于《中国能源统计年鉴》《中国环境统计年鉴》和各省市的统计年鉴,为剔除价格波动的影响,选取相应的价格指数来进行相关指标的平减.对于少数缺失的数据,利用线性插补或均值来进行处理.
2.2.1 被解释变量:绿色发展水平(GDL)
本文从投入、期望产出和非期望产出角度构建绿色发展水平指标体系,并运用SBM -DEA 模型测算具体数值,具体模型如下:
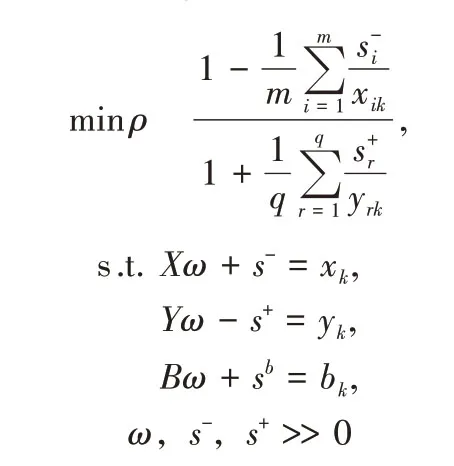
其中,ρ代表效率值,取值范围是0 到1,当ρ为1 时,表示决策单元强有效的;当其值小于1 时,表示决策单元在投入和产出上需要改进,并未到达理想状态;ω代表决策单元;s-代表投入变量的松弛变量;s+代表期望产出;sb代表非期望产出.
本文的投入指标考虑到创新,具体包括劳动投入、资本投入、能源投入、R&D 劳动投入、R&D 资本投入等指标,期望产出指标为地区GDP,非期望产出指标包括废气排放与废水排放.具体指标见表1.
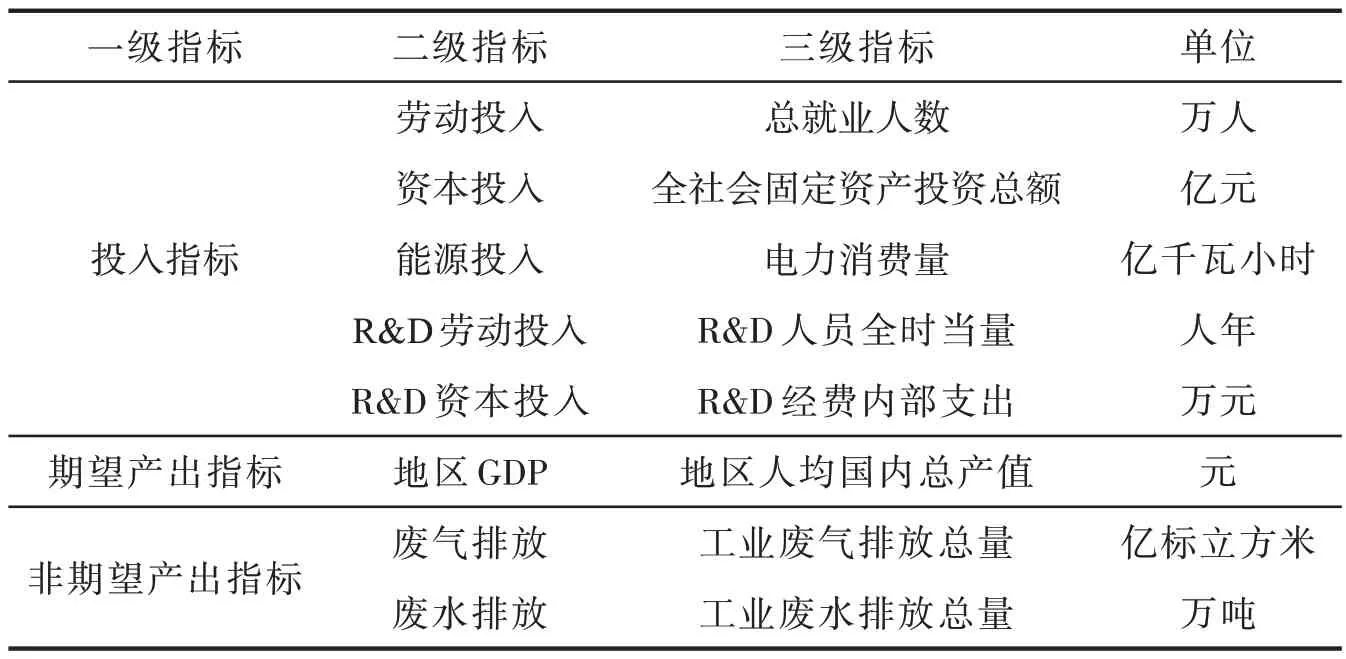
表1 绿色发展水平的投入产出指标
2.2.2 核心解释变量:碳排放强度(EI)
首先,对碳排放量进行测度,参照IPCC 推荐的依据燃烧的燃料数量以及缺省排放因子推算二氧化碳排放量,计算公式如下:
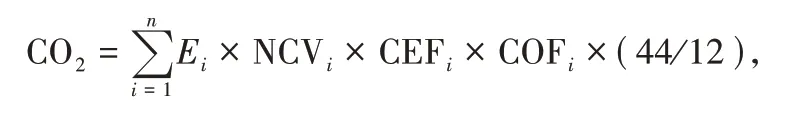
其中,CO2代表二氧化碳排放量;i代表能源种类,由数据可得性和计算的精确性,本文选取了煤油、焦炭、汽油、燃料油、柴油、天然气和原煤七种原料来进行测算;Ei代表能源i的消耗量(实物量);NCVi代表能源i的平均低位发热量;CEFi代表能源i的单位热值含碳量;COFi代表能源i的碳氧化因子;44/12 为二氧化碳气化系数.
各类能源的平均低位发热量取自《综合能耗计算通则》(GB/T2589-2020),单位热值含碳量和碳氧化因子来源于2006 年《IPCC 国家温室气体清单指南目录》.计算碳强度,即单位GDP 所产生的CO2排放量,计算公式如下:
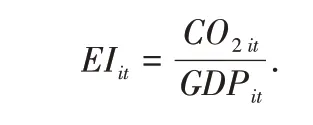
2.2.3 其他控制变量
参考李雪松等[2]和郝淑双等[3]的研究成果,本文选取控制变量及其具体描述如表2.

表2 控制变量的具体描述
3 实证分析
3.1 指标测算
3.1.1 绿色发展水平
将具体数据带入SBM -DEA 模型中测算出各区域绿色发展水平的具体数值,绘制出绿色发展在2008 年、2013年、2019 年以及各年份均值的演变情况,如图1 所示.从绿色发展水平的均值来看,重庆的绿色发展水平是最高的,上海次之,四川、安徽、江苏的绿色发展水平处于相对较低的水平,总体来看,长江经济带绿色发展的均值水平不是很高,有较大的提升空间.按照时间顺序来看,重庆市的绿色发展一直处于较高的水平,但是波动幅度稍大,易受相关因素的影响;上海市的绿色发展水平经历了从下降到上升再到下降的趋势,需要加大关注度,使其保持上升的态势;浙江省和贵州省的绿色发展水平降幅很大,应当找出下降的具体原因并进行修正;其余省份的绿色发展水平基本呈稳步上升态势,但上升幅度不大,需要采取措施以增加上升速度.
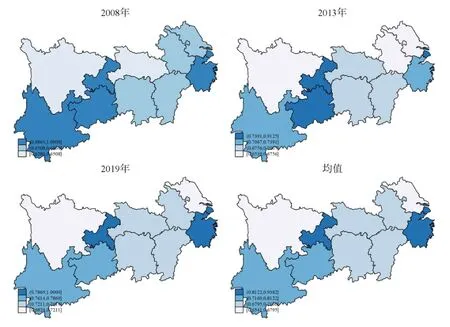
图1 长江经济带绿色发展水平演变情况
3.1.2 碳排放强度
根据具体数据测算出碳排放强度,将长江经济带划分为上、中、下游,上游包括重庆、四川、贵州和云南,中游包括湖北、湖南和江西,下游包括安徽、江苏、浙江和上海.按照全地区、上游地区、中游地区和下游地区计算平均值,绘制如图2 所示的折线图.
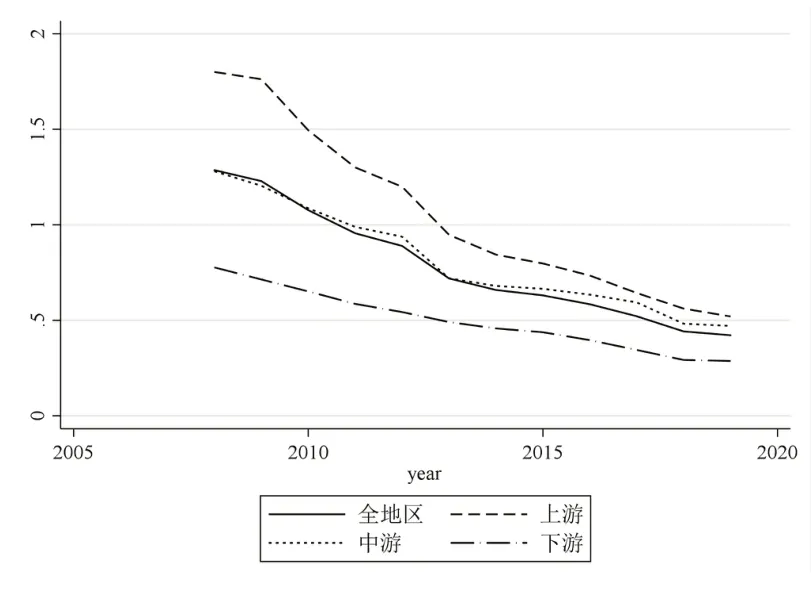
图2 长江经济带碳排放强度的变化趋势
从图中可以看出,上游地区的碳排放强度处于最高的水平,高于中游、下游和全地区的碳排放强度;中游地区的碳排放强度与全地区的碳排放强度水平基本相当,没有太大的差别;下游地区的碳排放强度要低于其他地区以及全地区.随着时间的推移,各区域的碳排放强度处于不断下降的状态,并且各区域之间的差别在不断地缩小,各地区的减排成效显著.
3.2 普通面板回归
3.2.1 描述性统计分析
对各变量进行描述性统计分析,结果见表3.为减弱异方差性,对部分指标进行取对数处理.由表3 可见,绿色发展水平取对数后的均值为-0.29,标准差为0.135,表明不同区域之间的绿色发展水平存在一定的差异性.碳排放强度的均值为0.785,标准差为0.484,不同地区间的CO2排放强度也存在区域性.
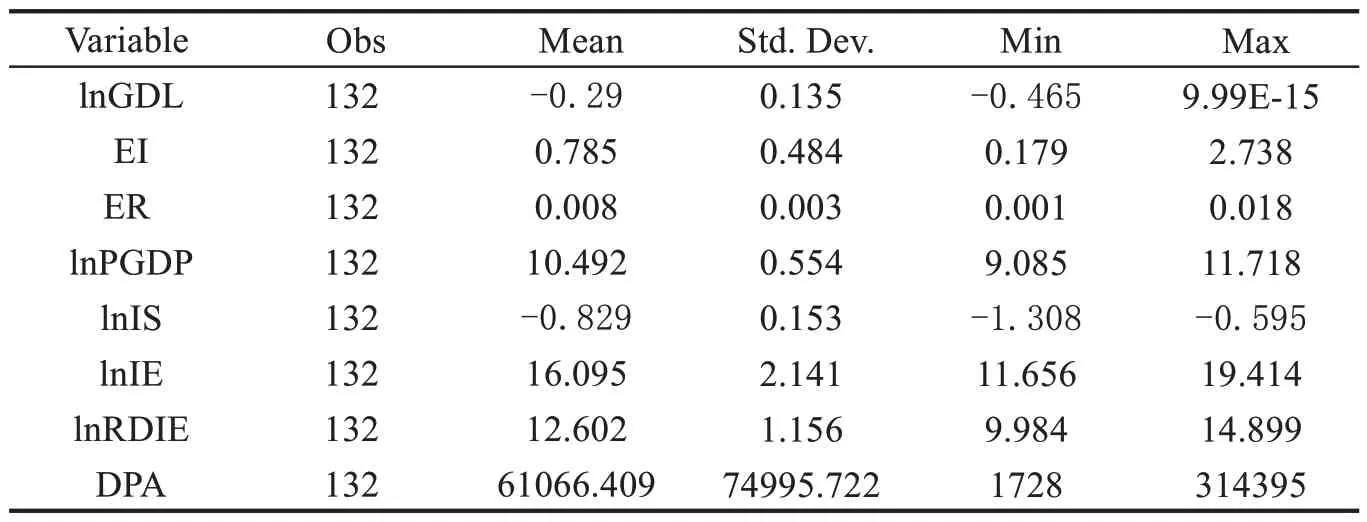
表3 变量描述性统计分析结果
3.2.2 基准回归分析
首先对数据进行平稳性检验,经验证各项数据均为平稳数据;接着进行Hausman检验,结果显示P 值为0.04 显著小于0.05,故而本文选择固定效应模型,具体结果见表4.色发展的水平.进出口的增加会显著增加绿色发展水平,可能是由于进出口拉动了经济发展.R&D 经费支出和专利申请授权数对绿色发展的影响系数都是显著为负的,可能是由于创新投入的利用率过低,从而创新投入的增加反而会拉低绿色发展水平.

表4 基准回归结果
观察表4的第(1)至(3)列可知,双固定效应回归、使用聚类稳健标准误的单项固定效应回归系数的方向与普通标准误的单项固定效应一致,只是部分变量的显著性水平有所下降.
3.3 空间杜宾回归
3.3.1 空间相关性分析
在进行空间回归前需要进行空间相关性分析,本文通过计算Moran’s I 指数进行检验.对绿色发展水平、碳强度、人均GDP 以及专利申请授权数进行检验,结果见表5.
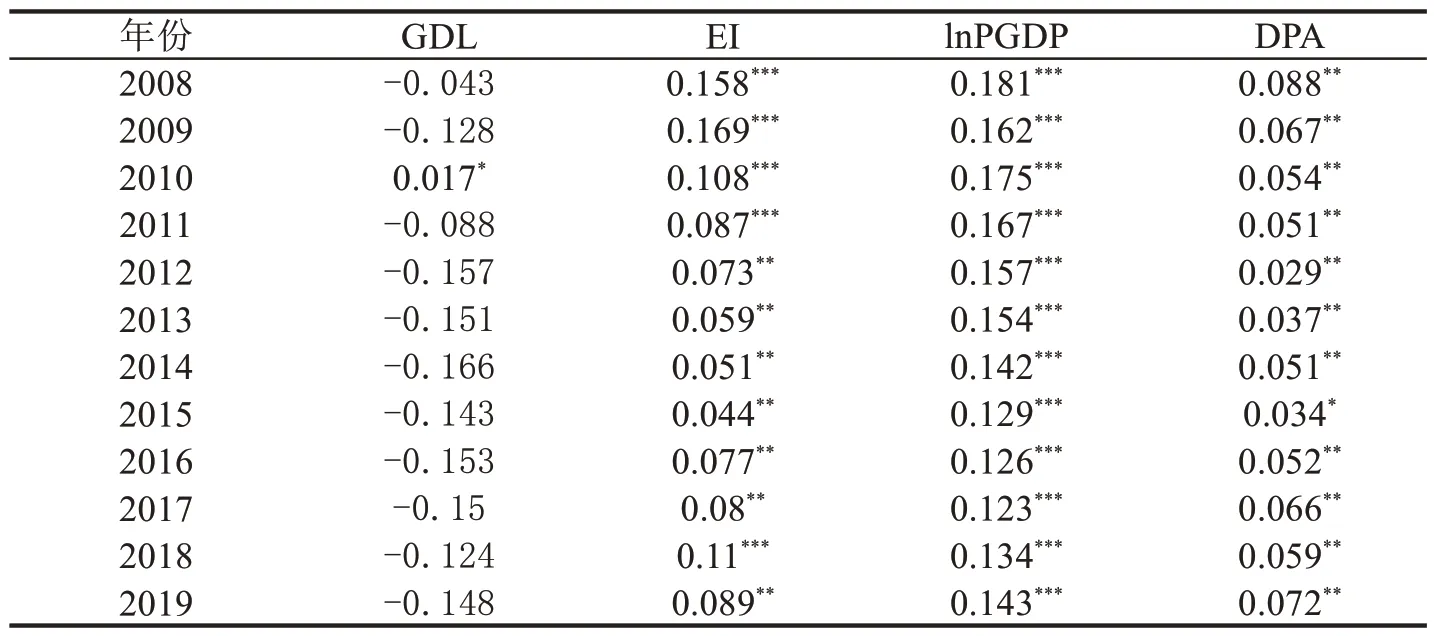
表5 莫兰指数结果
表4 第(1)列和第(2)列的区别在于,前者使用的是普通标准误,后者使用的则是聚类稳健标准误;第(3)列是在地区、年份双固定效应情况下的回归结果.
由表4 的第(1)列可知,从全地区范围来看,碳排放强度对绿色发展水平的负向影响不显著,而碳强度的平方项对绿色发展水平有显著正向影响,表明样本期间长江经济带的绿色发展水平随碳排放水平的提高呈现先升后降的“U”型曲线趋势.计算得到拐点位于碳排放强度为0.46 的水平上,当碳排放强度高于0.46 时,随着碳排放强度的降低,绿色发展水平也是降低的;当碳排放强度降低至0.46以下时,降低碳排放强度反而提高绿色发展水平.从控制变量角度看,环境规制对绿色发展的正向影响不显著;人均GDP 会对绿色发展水平产生显著正向影响,人均GDP提高会拉动绿色发展水平.产业结构对绿色发展水平有显著负向影响,因而需要适当调整产业结构,以提高当地绿
从表5 中可以看出,绿色发展水平的莫兰指数只有在2010 年是显著为正的,其他年份都不显著,即空间相关性不确定;但是碳强度、人均GDP 和专利申请授权数的莫兰指数在每一年都是显著为正的,存在较强的空间效应.基于此,可以进行后续的空间计量模型的回归.此外,本文选取的空间权重矩阵为地理距离矩阵.
3.3.2 空间面板回归结果分析
在对SDM 进行回归之前,需要进行相关检验.首先,进行LM 检验,结果见表6.表6结果显示大部分指标均在0.01的显著性水平上,拒绝了原假设,从而空间计量模型是适用的.其次,进行固定效应检验,结果均拒绝原假设,优先选用双固定效应模型.再次,进行Hausman 检验,结果并未显著拒绝原假设,表明采用随机效应的SDM 模型有一定的优势.最后,进行Wald 与LR 检验,结果均通过了显著性检验,因而SDM 模型不能转化为SLM 或SEM 模型.
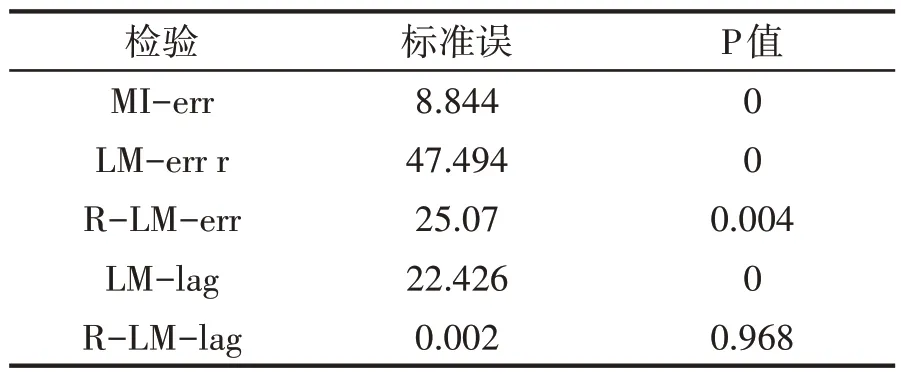
表6 LM检验结果汇总表
综上结果,本文运用双固定效应的SDM 模型和随机效应的SDM 模型来进行回归,并将SEM 模型、SLM 模型的回归作为参照对比,结果见表7.
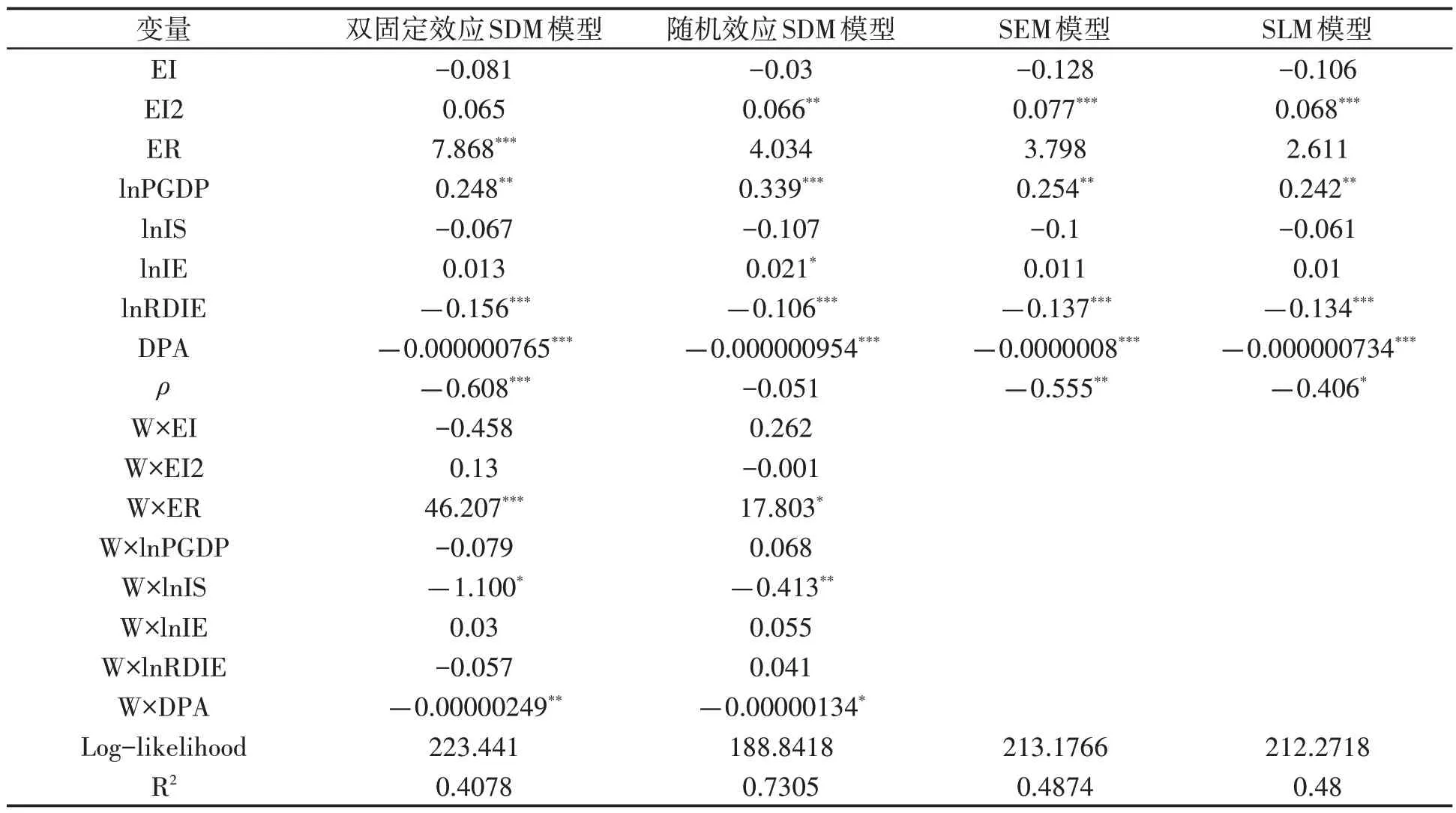
表7 空间计量模型回归结果
由表7 可知,SDM 模型的空间自回归系数显著为负,表明各地区之间的绿色发展水平会相互影响,各地区之间的绿色发展水平间的联系较为复杂;各模型的回归系数的正负较为一致、显著个数差别不大,因而选取双固定效应的SDM 模型较为合理.
在表8 中列出SDM 模型的直接效应、间接效应和总效应,以分析各变量对解释变量的影响.

表8 双固定效应SDM 模型下的直接效应与间接效应
首先,对于碳强度的一次项和二次项,其直接效应和间接效应的回归系数的正负同前文普通面板回归的系数正负是一致的,说明碳排放强度对本地和邻近地区的绿色发展水平的影响是一致的,都是呈“U”型,也即当碳强度降低到拐点之后,随着碳排放强度的降低绿色发展水平会提高.环境规制的直接效应和间接效应都显著为正,表明环境规制强度的增加既可以增加本地的绿色发展水平,也可以促进相邻区域绿色发展水平的提高.人均GDP 的直接效应显著为正,表明人均GDP 的增加可以促进本地绿色发展水平的提高,但对邻近地区无显著影响.R&D经费支出和专利申请授权数的直接效应均显著为负,也就是说会拉低本地的绿色发展水平,可能是对科研投入的利用效率不够高引起的,但是两者的间接效应均不显著.
3.3.3 基于不同区域的异质性检验
前文将长江经济带划分为上、中、下游,因此运用SDM 模型分别对各区域进行回归,结果见表9.
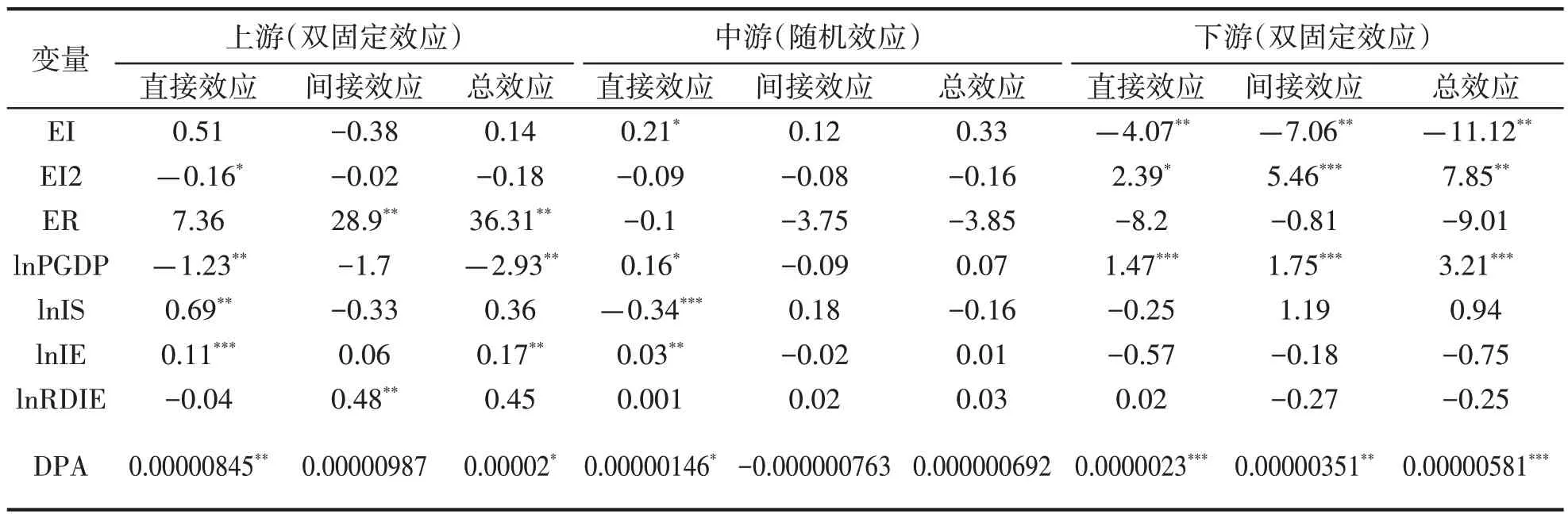
表9 基于不同区域的SDM 模型稳健性检验结果
关于碳排放强度的一次项和二次项,上游地区和中游地区的直接效应回归结果与整个长江经济带的直接效应回归结果是相反的,下游地区则与全地区相同,这表明在下游地区,碳排放强度对绿色发展水平的影响是“U”型的,降低到拐点前,碳排放强度降低会拉低绿色发展水平,降低到拐点后,碳排放强度降低则会推动绿色发展水平提高;而在上游地区和中游地区,碳排放强度对绿色发展水平的影响是倒“U”型的,绿色发展水平在降低到拐点前随着碳排放强度的降低而提高,在降低到拐点之后则随着碳排放强度的降低而降低.这表明在不同的区域,碳强度对绿色发展的影响存在不同的效果,因此各区域需要结合实际,制定不同的发展政策.
关于其他变量的回归系数,各区域与全区域有一定的差异,但是区别不大.
4 结论与启示
本文以长江经济带各省市2009—2019 年为样本区间,测算了绿色发展水平、碳排放强度等变量的具体数值,考察了碳强度对绿色发展水平的空间影响效应,实证结果可以为长江经济带各地区实施绿色低碳可持续发展政策提供一定的经验证据.
4.1 结论
(1)在样本期间,长江经济带各区域的绿色发展水平存在一定差异性,上游地区处于较为领先的地位,随着年份的推进,各地的绿色发展水平也存在相应的波动性.
(2)关于各地区的碳排放强度,上游地区的碳排放强度处于最高的水平,高于中游、下游和全地区的碳排放强度;中游地区的碳排放强度与全地区的碳排放强度水平基本相当;下游地区的碳排放强度要低于其他地区以及全地区.此外,各区域的碳排放强度有不断下降的趋势,各地区的减排成效显著,并且各区域之间碳强度的差别在不断地缩小.
(3)碳排放强度对本地和邻近地区的绿色发展水平的影响都呈“U”型,在到达拐点之前,碳强度降低时,绿色发展水平也会随之下降,在碳强度降低至拐点之后,碳强度的降低就会拉动绿色发展水平提高.
(4)环境规制对绿色发展水平有显著正向影响,环境规制强度的增加不仅可以增加本地的绿色发展水平,还可以促进相邻区域绿色发展水平的提高.
(5)人均GDP 的增加只会促进本地绿色发展水平的提高,对附近地区没有显著影响.
(6)RD 经费支出和专利申请授权数会拉低本地的绿色发展水平,但是对邻近地区的绿色发展水平影响不显著.
4.1 启 示
首先,由于碳排放强度对绿色发展水平的影响存在拐点,各地针对自己的经济环境发展状况确定具体的拐点,并尽快将碳强度降低到拐点之后,这样碳强度的下降才会带来区域绿色发展水平的提高,在拐点之前碳强度下降会拉低区域绿色发展水平.其次,环境规制强度会推动区域绿色发展,环境规制强度的增加可以促进本地和相邻区域的绿色发展水平的提高,因此需要制定适当的环境资源保护政策,以拉动当地和邻地的绿色发展水平.再次,人均GDP 的增加会促进本地绿色发展水平的提高,因此需要拉高地区生产总值和地区人均生产总值,以推动本地绿色可持续发展.最后,重视R&D 经费支出和专利申请授权数对区域绿色发展水平的阻碍作用,今后应当更加充分合理地利用创新投入,防止创新投入不必要的浪费.

