线性抽样法重构传导边界非均匀可穿透障碍物

叶建国，邓 霞

(1.喀什大学数学与统计学院，新疆 喀什 844000；2.长沙师范学院数学科学学院，湖南 长沙 410100)

散射理论是20世纪数学物理研究的重要领域之一.一百多年来，从Rayleigh 对天空是蓝色的解释，到Rutherford 对原子核的发现，再到现代医学CT 的应用，声波和电磁波散射问题的研究越来越受到人们的关注，在地球物理、遥感技术、医学成像、无损探测、工业控制等领域有着广泛的应用[1-6].本文探讨了带有传导边界条件的非均匀可穿透障碍物线性抽样法重构问题.

1 问题的描述

设有界单连通区域Ω是R2中的可穿透障碍物，其边界∂Ω为C2光滑的.障碍物Ω内外的介质不一样，其表面涂有薄的、高导电率的物理涂层，当入射方向为d ∈S1:={x∈R2:|x|=1}的时谐声波（平面波）ui=eik1x⋅d遇到障碍物时，在障碍物的边界∂Ω会产生传导边界条件，该非均匀可穿透障碍物散射问题的模型可用Helmholtz方程的边值问题描述为

其中：波数kj>0(j=1,2)由波的频率ω与波在区域Ω外和内的介质中的波速cj之比定义，由于Ω内外的介质不同，则有k1≠k2；电导率λ>0，表示障碍物表面物理涂层的性质；传输系数η>0，由Ω内外的介质的密度之比定义；n表示边界∂Ω的外单位法向量，.全波场U:=ui+us是给定的入射波ui和与之相应的散射波us之和，“±”表示x沿法线方向从Ω的外（内）逼近边界∂Ω.此外，假设散射波us满足Sommerfeld衰减条件

事实上，取u(x):=us(x)，v(x):=V(x)，f1:=-ui和，则问题(1.3)转化为问题(1.1)和(1.2).

邓霞等在文献[7]中对传输系数η=1 用边界积分方程方法[5]对问题(1.1)—(1.2)适定性做了研究.由于边界积分方程法对相关参数是常数均使用，显然当η>0也可得到问题解的存在唯一性.

逆散射问题是利用测量数据（远场模式）重构散射体的形状、位置和物理参数等.对给定的入射波ui，散射波us有渐近表示

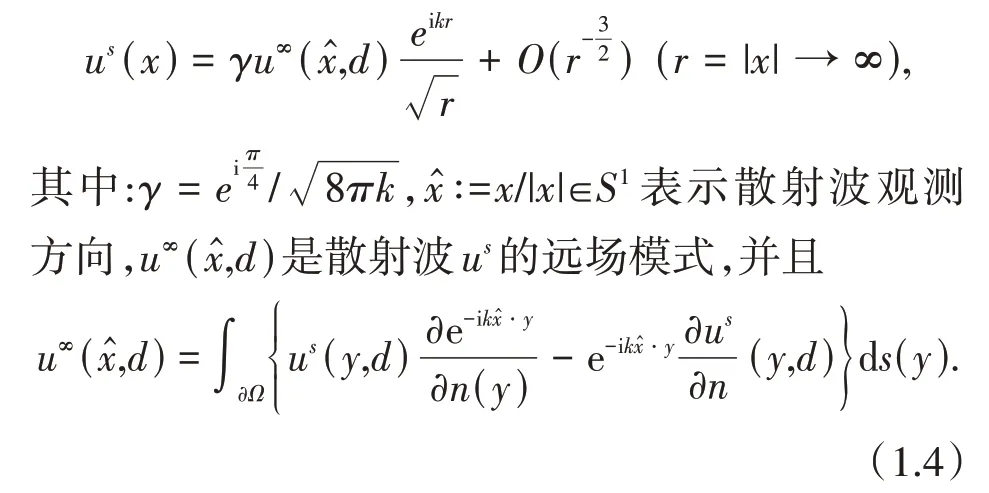
逆散射问题传统的解法有Newton 迭代法[8-9]，该方法需要知道散射体的先验信息，这给实际应用带来很大的限制.1996 年，Colton 等利用线性抽样法重构了不可穿透散射体[10].由于该方法不需要知道散射体的先验条件，且简单易行，引起了研究者的关注.此外，因式分解法[6]近年来越来越多的应用到逆散射问题中.Cakoni 等的专著[5]论述了线性抽样法的详细理论知识和具体运用.线性抽样法解反散射问题的主要思想是用Tikhonov 正则化方法求解远场方程

2 线性抽样方法的理论基础

逆散射中的线性抽样法的关键是验证远场算子F其分解算子满足紧性、单射性和值域的稠密性等性质.

2.1 定义

定义2.1任意的g∈L2(S1)，远场算子F:L2(S1) →L2(S1)定义为

定义2.2定义边值算子

其中u∞是传导边值问题（1.3）散射场us对应的远场模式.

定义2.3任意的g∈L2(S1)，辅助算子

由叠加原理知，远场算子F分解为

由经典的椭圆方程理论知，当波数不是内Dirichlet问题

定义2.4内Dirichlet-to-Neumann（DtN）算子定义为，其中v满足问题（2.5）.

定义2.5内Neumann-to-Dirichlet（NtD）算子ΛN:H-1/2(∂Ω) →H1/2(∂Ω)定义为ΛNh=v|∂Ω,其中v满足问题（2.6）.

显然，在H-1/2(∂Ω)中ΛDΛN=I和在H1/2(∂Ω)中ΛNΛD=I.

2.2 假设

假设2.1即不是问题（2.5）的Dirichlet特征值，也不是问题（2.6）的Neumann特征值.

假设2.2不是下列内传输边值问题的特征值

Xiang等在文献[11]中对问题（2.7）传输特征值的离散性和存在性做了深入的研究.

2.3 引理

引理2.1[12]若假设2.1 和2.2 成立，则边值算子G是紧算子，值域R(G)在L2(S1)中稠密，并且核空间为

G的紧性由椭圆算子的内正则性理论容易得到.由文献[12]定理2.1和2.2知引理成立.

引理2.2对任意的z∈R2，z∈Ω当且仅当ϕz∈R(G).

证明设z∈Ω，令

其中Φk1(x,y)是Helmholtz方程

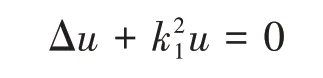
的基本解.则由远程方程的定义知

设ϕz∈R(G) 满足则存在(f1,f2)∈H1/2(∂Ω)×H-1/2(∂Ω)使得G(f1,f1)T∈R(G).设(u,v)是问题（1.3）带有边值(f1,f2)的解，则由问题（1.3）的适定性知在R2中u(x)=Φk1(x,z).由散射场u的解析性与事实Φk1(x,z)在z=x∈R2处爆破相矛盾，故引理得证.

线性抽样法理论要求算子G具有单射性，而传导边值问题（1.3）却不能满足G的单射性[12].有了算子G的核空间Ker(G)的刻画，算子G有如下分解：

定理2.1[12]若假设2.1 和2.2 成立，则修正的边值算子:H12(∂Ω) →L2(S1)是紧的单射算子，值域R()在L2(S1)中稠密，并且对任意的z∈R2，z∈Ω当且仅当ϕz∈R().

定理2.2若假设2.1 和2.2 成立，则辅助算子是紧的单射算子，并且值域R()在H1/2(∂Ω)中稠密.

证明（1）由算子H1和H2的积分核eik1x⋅d的连续性知，=H1-η-1ΛNH2是紧算子.

（2）设任意的g∈L2(S1)，使得=0.即在∂Ω上H1g-η-1ΛNH2g=0.记p:=H1g，q:=H2g,则ηp-ΛNq=0.由假设2.1 知，对f=p和h=q，问题（2.5）和（2.6）存在唯一解vp∈H1(Ω)和vq∈H1(Ω)，则（即ΛNq=vq|∂Ω）.令v=ηvp-vq，则有

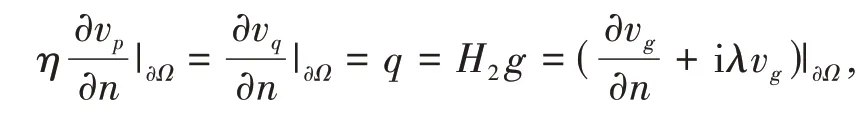
从而(vg|Ω,vp|Ω)满足边值问题

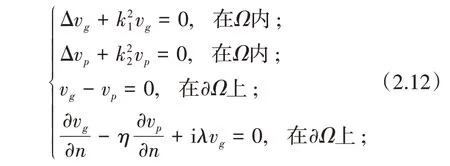
（3）只需证明的伴随算子:H-1/2(∂Ω) →L2(S1)是单射[5].设任意的g∈L2(S1)，h∈H-1/2(∂Ω)，因为

故引理得证.

由假设2.1和2.2以及定理2.1和2.2，我们得到线性抽样法重构散射体Ω的重要结论.

定理2.3若假设2.1 和2.2 成立，则对任意的z∈R2，ϕz∈L2(S1)，

（1）若z∈Ω，则对任意的ε>0，存 在，满足

（2）若z∈R2，则对任意的ε>0，存在，满足

故定理2.3 得证.

3 数值模拟

本节我们验证线性抽样法可以重构散射体的边界，这种反演方法可以快速有效地确定散射体的形状和位置.线性抽样法数值计算的相关理论参看Cakoni 的专著[5].下面给出具体算法分析.

第一步：计算远场.用边界积分方程法生成边值问题（1.3）的等价边界积分方程Aψ=P，求出散射场u，进而求出远场u∞.

第二步：离散化.用Nyström 算法，将A中的边界积分算子离散.将u∞用三角级数表示为，并对傅里叶系数添加随机扰动(其中ε是参数，χn是取值在[-1,1]内满足均匀分布的随机扰动),从而得到远场的近似逼近值

第四步：奇异值分解.将进行奇异值分解为=UΛV*(其中U,V是酉矩阵;对角矩阵Λ=diag(λ1,λ2,…,λn))，则

第五步：正则化解.令

则求解（3.3）的正则化解等价于求极小解

其中α为Tikhonov 正则化参数，由Morozov 差异化原理决定.定义uz=V*gz，记(λj,ϕj,ψj) 是Λ的奇异系统，则由Picard 定理知（3.5）存在极小解，带入分量可得

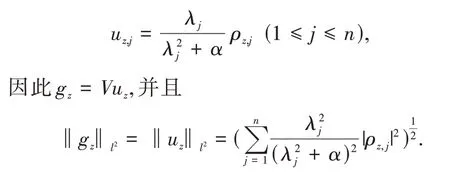
第六步：障碍物重构.由定理2.3 知，当||gz||l2的值非常大时,抽样点z逼近障碍物边界.因此,我们可以给定一个阀M,画出满足的等高线,从而可以得到重构的形状.

下面我们分别选取散射体的边界为风筝形(1.5 cost+0.975 cos 2t,2.25 sint)、方形(2.55(cos3t+cost),2.55(sin3t+cost)) 和圆形(3 cost,3 sint)，用Nyström 算法求解正散射问题,得到无穷远场离散值，并且都位于单位圆上.在整个数值模拟过程中传输系数η=2，考查其他参数的变化对数值模拟的影响.

在图1中，设定参数λ=1,k1=3,k2=1 分别对风筝形、方形和圆形散射体边界重构.线性抽样方法都能适用,重构图形的清晰度没有明显的区别.

图1 形状不同的散射体边界的重构

在 图2中，设定参数λ=1 和k1=3 固 定,内部波数k2变化,对风筝形边界重构.波数k2=3 时,反演图形的清晰度较差.从前面理论分析可知我们在重构散射体边界时一定要避免内特征值问题,当波数k2与内特征值一致或者接近时,会影响重构的效果.

图2 内部波数不同的风筝形散射体边界的重构

在图3中，设定参数k1=3 和k2=0.5 固定,阻抗系数λ变化,对方形边界重构.从图中发现阻抗系数λ的变化对反演的效果影响不显著.

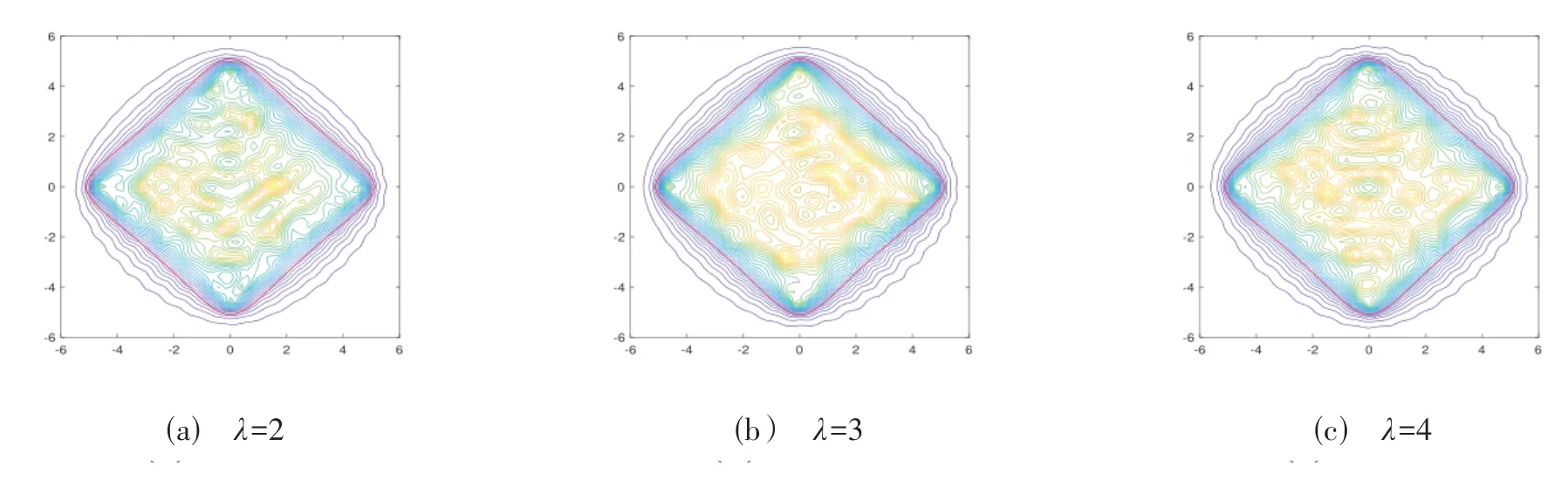
图3 电导率不同的方形散射体边界的重构

在图4 中，设 定参数λ=1 和k2=1 固 定,外部波数k1变化,对圆形边界重构.波数k1增大时,反演图形的清晰度较差.所以入射波的频率变化会影响反演效果.

图4 外部波数不同的圆形散射体边界的重构