犹豫模糊语言术语集中考虑专家权重的决策方法
朱国成 ,赵瑞华
(1.广东创新科技职业学院科学技术协会,广东 东莞 523960;2.云安中学生物组,广东 云浮 525700)
0 引言
自2010 年Torra[1]提出犹豫模糊集(Hesitant Fuzzy Sets,HFS)概念(可以使用多个不同的隶属度来表达决策群体对某事物的认知程度)以来,其在多属性群决策(Multi-Attribute Group Decision Mak⁃ing,MAGDM)问题中得到了广泛应用[2-4].在具体的决策问题应用中学者使用不同类型的信息数据刻画隶属度值,例如,文献[5]采用精确数据刻画隶属度并建立了犹豫模糊互补判断矩阵(HFCJM)决策模型,文中排序结果对比表明模型决策效果较好;文献[6]使用区间数作为隶属度值,提出了一种改进的ELECTRE 方法来解决多属性决策问题;在应用HFS解决MAGDM 问题过程中,描述隶属度的信息数据还有三角模糊数[7]、梯形模糊数[8]、语言评价术语集[9]等.在犹豫模糊语言术语集多属性群决策(Hesitant Fuzzy Linguistic Terms Sets Multi-Attribute Group Decision Making,HFLTSMAGDM)问题中,通常做法是将语言术语换算为对应的数据信息再采用集结算子对属性的综合数据信息进行糅合,通过比较糅合数值结果达到排序方案目的.截止目前,在解决HFLTSMAGDM 问题的过程中,将语言评价术语转换成对应数据信息过程中鲜有学者考虑隶属度为语言评价术语时其关联的决策专家权重问题,事实上,决策过程中对于不同专家的偏好时有发生,怎样解决此类问题,本文进行了有益尝试,并用不同算法对此类问题进行了分析,以期为今后的进一步研究提供参考.
1 预备知识
定义 1.1[10]令X为预知集合,A=为X上定义的HFS,其中hA(x)是在区间[0,1]中不同数值构成的集合,x属于集合A的可能隶属度用里面具体数值表示.称hA(x)为一个犹豫模糊元(Hesitant Fuzzy Elements,HFE).
定义1.2[11]设S={si|i=0,1,…,2τ}是由粒度为2τ+1个语言术语组成的集合(粒度是指术语的个数),S满足以下运算特征:
(1)逆运算si=neg(sj) ⇔I(si)+I(sj)=2τ;
(2)有序性si≤sj⇔I(si)≤I(sj);
(3)最大值max(si,sj)=si,当si≥sj;
(4)最小值max(si,sj)=si,当si≤sj.
定义1.3[12]语言评价术语采用九段制,为了突出较差与较好程度模糊性,在转换成区间数时加大区分力度,具体对应转换分数如表1所示.

表1 语言评价术语转换表
定义1.4[13],称为一个区间数.特别地,若aL=aU,则退化为一个实数.区间数运算法则如下:设=[aL,aU]和=[bL,bU],且λ≥0,则

定义1.5[14]区间数a=[a-,a+],b=[b-,b+],称

定义1.7令ai(i=1,2,…,n)为一组非负实数,且r=1,2,…,n.若

则称(1)式为Maclaurin 对称平均算子,其中:i1,i2,…,ir为遍历组合1,2,…,n中的一切r元组;为二项式系数.
由式(1)可知,Maclaurin 对称平均算子有下列性质:
(1)对于任意的i,若ai=a≥0,则
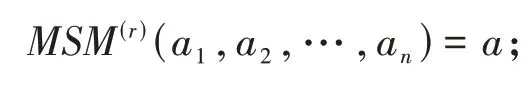
(2)对于任意的i,若0 ≤ai≤bi,则有
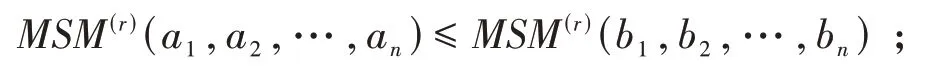
(3)对于任意的ai≥0,有≤Max(a1,a2,…,an).

2 主要方法与结论
2.1 算法一
2.1.1 问题陈述及相关定义
在MAGDM 问题中,设决策专家集Z={z1,z2,…,zλ,…,zT},其权重用ωzλ表示且已知;设决策方案集为A={a1,a2,…,ai,…,aM},属性集为G={g1,g2,…,gj,…,gN},属性权重用符号ωgj表示且未知;决策专家组给予第i个方案的第j个属性的评价信息用HFLTSsij表示,HFLTSsij中的元素定义为本文考虑的属性类型皆为效益型,有如下定义:
定义2.1根据定义1.3 将评价信息HFLTSsij中的隶属度LTS 转换为对应的区间数(Interval Numbers,IN),构成区间犹豫模糊元(INHFE)hij,hij=#hij表示INHFEhij中的元素个数,表示区间犹豫模糊数(INHFN),显然有对应关系
定义2.2确定属性的理想属性值(继续用区间数表示),具体计算方法为

其中,k,k′∈{1,2,…,#hij};i,i′∈{1,2,…,M}.
2.1.2 计算属性权重


证明(1)(2)证明略.
(3)因为

2.1.3 算法步骤
步骤1 根据定义1.3将评价专家给予方案的评价信息表转换为决策矩阵[hij]M×N;
步骤2 由2.1.2节内容计算属性权重ωgj;
步骤3 计算HFE的加权综合值

步骤4 采用定义1.7对进行集结,得结果

由式(1)集结性质可知,f(ai)大者其对应的方案为优.
2.2 算法二
2.2.1 问题陈述及相关定义
陈述内容与算法一一致,有以下扩展定义:
定义2.5由定义2.1 计算INHFEhij的综合值,为了完整保留INHFEhij的决策信息,其综合值仍用区间数表示为

定义2.6确定属性理想属性值(继续用区间数表示),确定方法为

2.2.2 计算属性权重
步骤2 采用文献[16]中的方法,将相离度矩阵[dij]M×N规范化为矩阵[uij]M×N,这里显然有

2.2.3 算法步骤
步骤1 根据定义1.3将评价专家给予方案的评价信息表转换为决策矩阵[hij]M×N.
步骤2 由2.2.2节知识计算属性权重ωgj.
步骤3 为了进行此步工作,需要给出以下几个定义:

根据定义2.7、2.8、2.9 最终确定INHFEhij的有效加权综合值|hij|.
步骤4 利用定义1.6,对不同方案进行测度,测度形式为
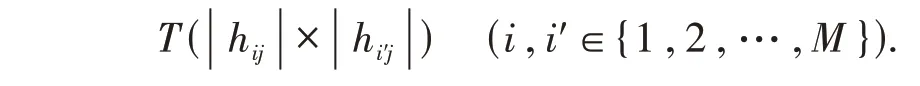
步骤5 统计T(|hij|×|hi′j|) >1的个数(Qii′,i,i′∈{1,2,…,M}),根据之间的大小比较各方案优劣,

(1)当T+(ai,ai′)>T-(ai,ai′)时,说明方案ai优于方案ai′;
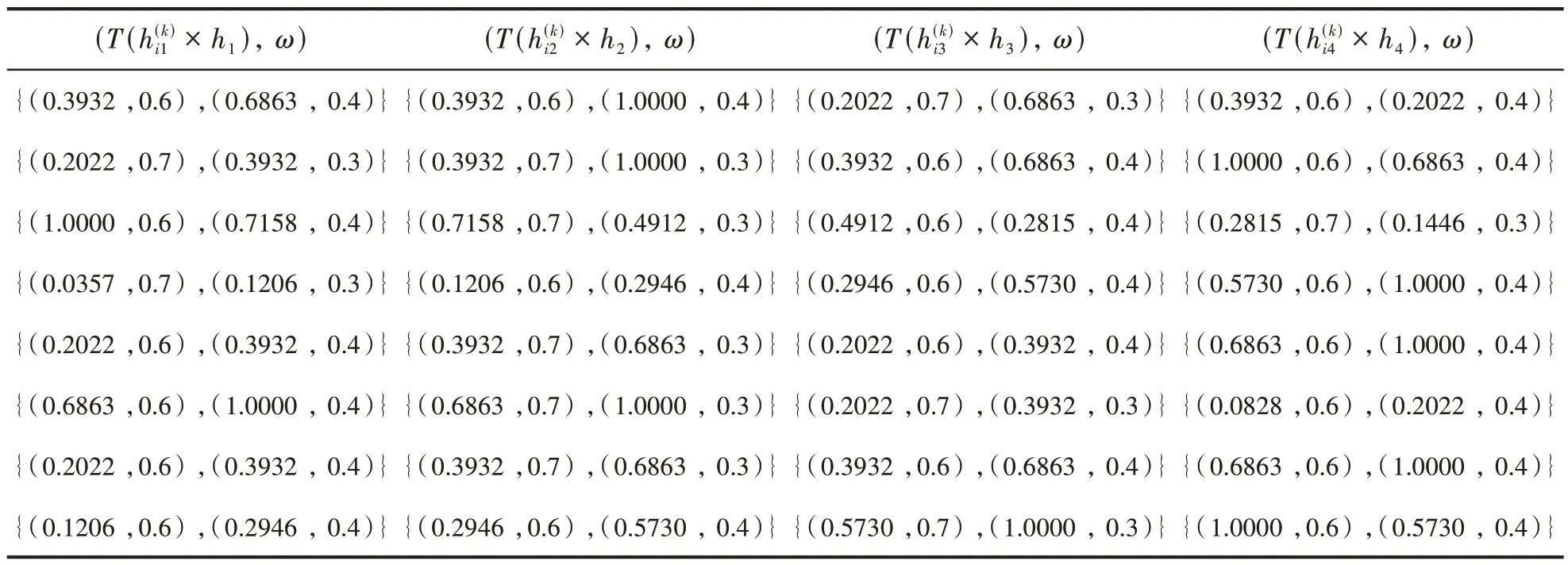
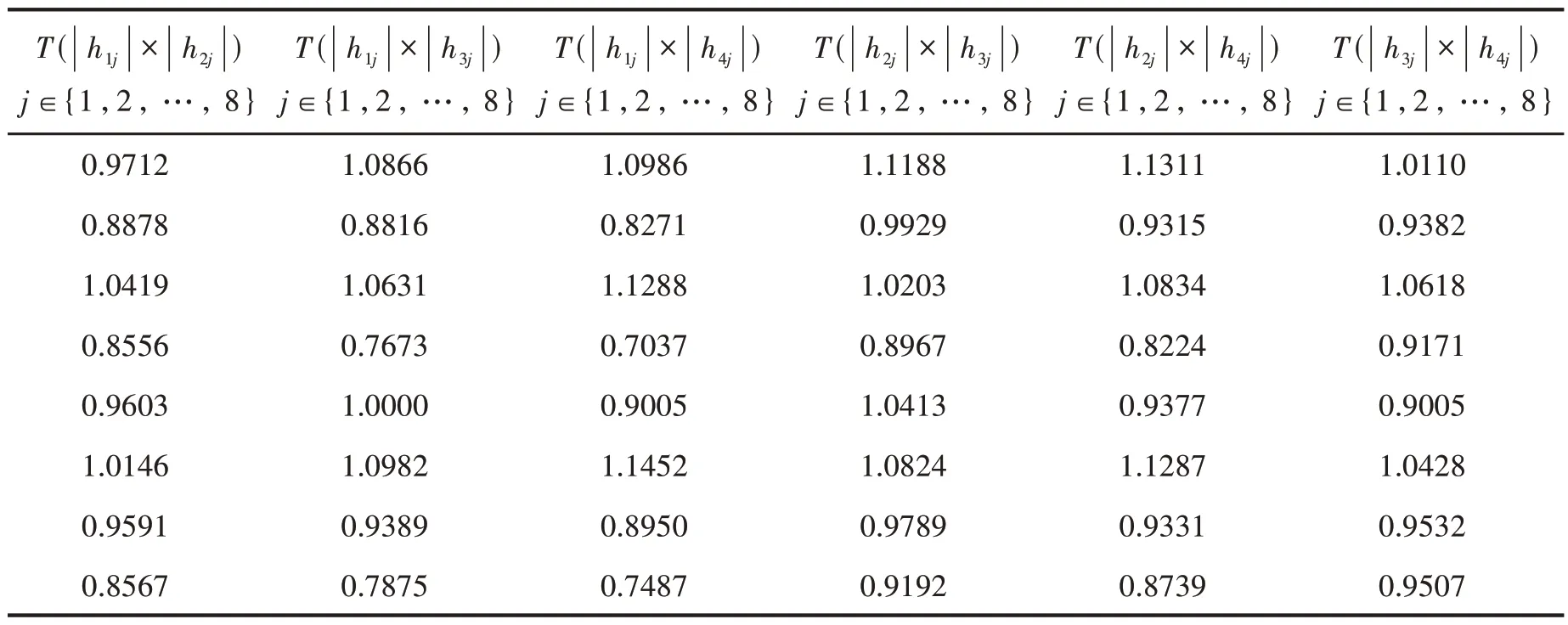
(2)当T+(ai,ai′) (3)当T+(ai,ai′)=T-(ai,ai′)时,说明方案ai与方案ai′等同. 高考结束以后,考生对于高等学校的选择是全家的“头等大事”,在众多高校当中,考生能够怎样科学高效的选择适合自己的学校是一个决策问题,为了将全家的“头等大事”做好,则全部家庭成员参与决策.一个家庭有4位成员,分别是哥哥、妈妈、爸爸以及妹妹,在群决策问题中4 位成员用符号zλ(λ=1,2,3,4)表示,其权重ωz1=0.5,ωz2=0.2,ωz3=0.2,ωz4=0.1.根据哥哥的成绩,全家筛选出4 所学校(a1,a2,a3,a4)(决策方案)供选择并排序,对于学校的考察主要从学校排名(g1)、专业实力(g2)、区位优势(g3)、学 费(g4)、校园环境(g5)、住宿条件(g6)、办学历史(g7)以及学校名称(g8)等8 个方面(属性)考虑,其权重ωgj(j=未知,1,2,…,8)各位家庭成员根据自己的思考给出语言术语信息,利用本文知识解决此决策问题,评价信息见表2(具体符号语言信息意义见表1). 表2 语言术语评价信息表 3.1.1 计算属性权重 步骤1 根据定义2.1,将表2中语言信息转换为IN 信息数据并将家庭成员以其权重之和表示,见表3. 表3 转换表 步骤2 确定属性的理想属性值hj并让与属性的理想属性值hj进行测度及测度结果关联的决策专家权重,结果见表4. 表4 测度表 步骤3 计算HFE的几何距离函数值e()与离差程度函数值d()分别为 步骤4 由式(5)、(6)可得各属性的权重分别为 3.1.2 算法步骤 步骤3 利用定义1.7 计算f(ai)(不失一般性,这里取r=1)如下: 由f(ai) 大小比较可知,各方案优劣排序为a4≻a3≻a2≻a1. 3.2.1 计算属性权重 步骤1 由定义2.6计算出如下各个属性的理想属性值、根据表3 可得综合值矩阵[]4×8及相离度矩阵[dij]4×8. 步骤3 计算gj上的熵值sj及其权重ωgj依次为 3.2.2 算法步骤 步骤1 属性权重ωgj已经算出,确定INHFEhij的有效加权综合值|hij|分别为: 步骤2 测度T(|hij|× |hi′j|),i,i′∈{1,2,3,4},j={1,2,…,8},绘制测度表见表5. 表5 测度表 步骤3 统计T(|hij|×|hi′j|) >1 的个数Qii′(i≠i′,i,i′ ∈{1,2,…,8}),得 由判定规则可知方案排序分别为a1≺a2,a1≺a3,a1≺a4,a2≺a4,a3≺a4,因为Q23=故依据Q23无法判断方案a2,a3之间的优劣,考虑到 有T+(a2,a3)>T-(a2,a3),即a2≻a3. 综上可得方案排序为a4≻a2≻a3≻a1. 本文针对HFLTSMAGDM 问题,建立了两种算法,两种算法在决策前都需要将LTS信息转换为对应的区间数而后再进行运算.算法一利用积型贴近度公式将HFN 与HFE 的理想值进行测度,把测度结果与之对应的决策专家权重看作二维变量并以点坐标形式书写,在考虑HFE 的整体值大小与其元素之间离差程度大小基础上计算属性权重,考虑的因素比较全面,故具有很强的说服力,最后通过Maclaurin 对称平均算子集结方案各属性的加权综合值.算法二采用经过处理的HFN 值构造区间数并利用区间数熵值法计算属性权重,通过统计各方案在相同属性上进行测度的结果数量来判定方案优劣. 综上研究表明,两种算法在确定属性权重方面差异明显,但是都能快速取得排序结果,同时对于最优方案与最差方案的认同也完全一致.这说明两种算法计算属性的权重差异只影响处于排序中间的方案顺序,决策过程中决策者可以根据决策环境灵活选择决策算法以满足决策需求.算法一对于各HFE 中元素数量不同的问题还需要进一步研究;算法二在属性中存在“一票否决”式重要程度的属性,决策算法不再适用(对于在教师评优评先及职称晋升的决策问题中,师德这一评价属性就是一票否决的,但是,如果在评选的所有教师中,师德皆没有问题,则可以使用该方法).在HFS中,将隶属度发生的可能性作为变量添加之后称之为概率犹豫模糊集(PHFS,见文献[17]),概念从决策专家数量层面进行的思考.本文从决策专家整体重要性的角度出发,进行了决策算法应用研究,后续针对两者之间的关系及差异还将做进一步深入研究.3 案例分析

3.1 算法一

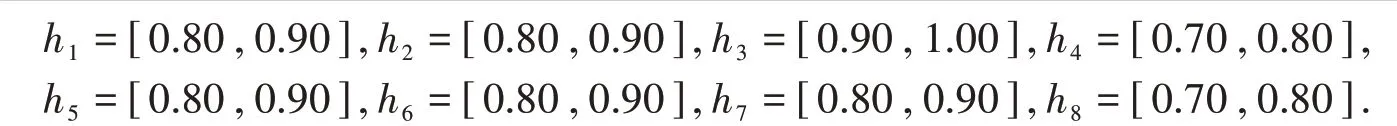





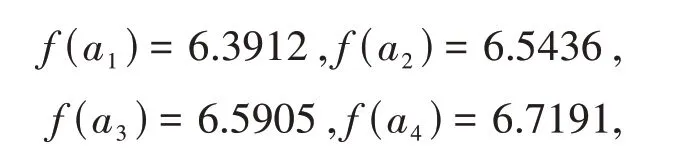
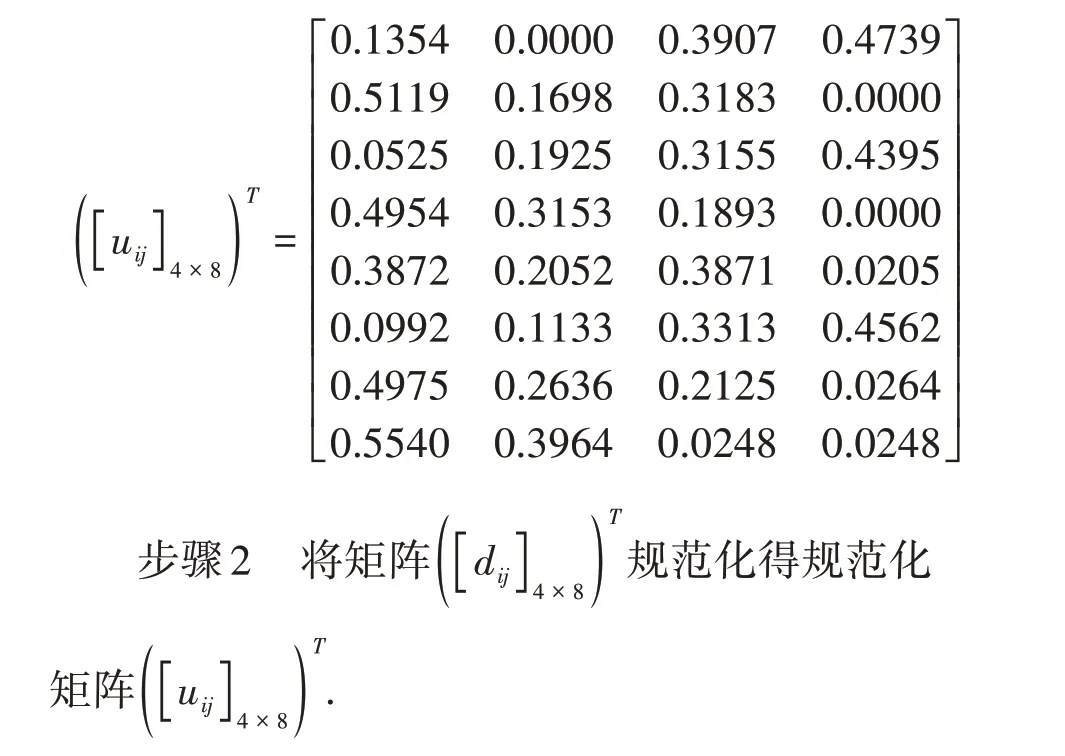
3.2 算法二

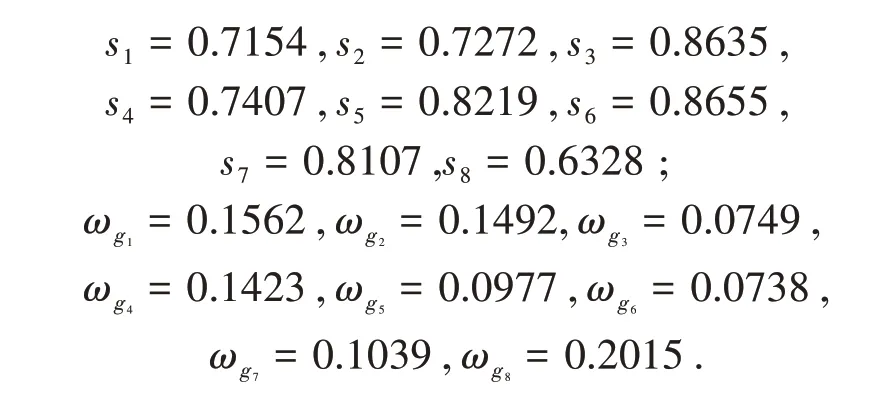


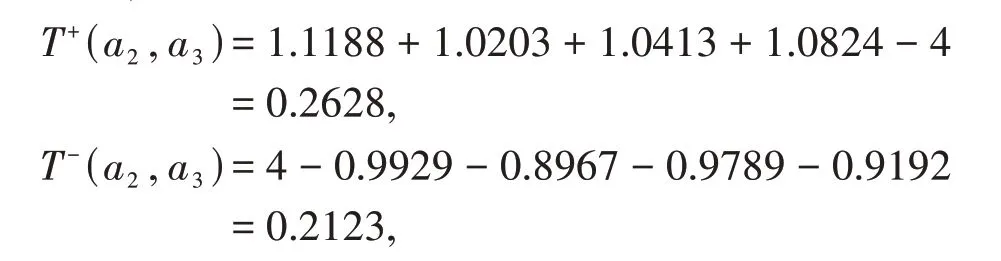
4 结论

