反次Hermite矩阵方程的求解

马 跃， 黄晓芬,2

(1.海南师范大学数学与统计学院,海口 571158；2.海南师范大学数据科学与智慧教育教育部重点实验室,海口 571158)

1 引 言

矩阵是数学中一种基本的工具, 对于数学学科的重要性不言而喻, 而且在计算机学科和物理学科中也有着广泛的运用. 例如, 在计算机学科中, 矩阵会被用到三维动画的制作. 在物理学科中, 电路学的电路方程的矩阵形式可以更好的被用来研究割集电压方程、列表方程回路、电流方程和结点电路方程的矩阵形式. 另外Hermite矩阵因其特征值为实数通常用于量子物理中. 因此对Hermite矩阵及其相关矩阵进行研究讨论是非常必要的. 目前人们对于Hermite矩阵方程、反Hermite矩阵方程、次Hermite矩阵方程均已得到求解[1-3]，且得到相应解的表达式. 本文针对一种反次Hermite矩阵方程解的表达式以及解的存在性条件进行了讨论.

2 预备知识

定义1[2-4]如果复矩阵A满足A*=A,则复矩阵A叫做Hermite矩阵,A*表示A的共轭转置矩阵.

定义2[2-4]如果复矩阵A满足A*=-A,则复矩阵A叫做反Hermite矩阵,A*表示A的共轭转置矩阵.

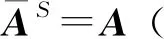
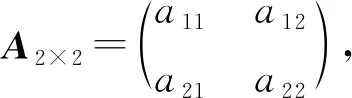
注 (AS)S=A， (A-1)S=(AS)-1， (A+B)S=AS+BS， (AB)S=BSAS.

引理1[2-5]已知矩阵方程

XAY=A,

(1)

其中A为可逆矩阵,P为任意矩阵，使A+P和A-P均为可逆矩阵,则X=(A+P)(A-P)-1和Y=(A+P)-1(A-P)是方程(1)的解.

引理2[2-5]已知复数域上矩阵方程

X*AX=A,

(2)

这里A为非退化复Hermite矩阵,P为任一反Hermite矩阵, 且使A+P和A-P均为可逆矩阵, 则K=(A+P)-1(A-P)为方程(2)的解.

引理3[1-5]已知复数域上矩阵方程

X*AX=A,

(3)

这里A为非退化复反Hermite矩阵,P为任一Hermite矩阵, 且使A+P和A-P均为可逆矩阵,则K=(A+P)-1(A-P)为方程(3)的解.

引理4[2-5]已知矩阵方程

(4)

其中A为非退化复次Hermite矩阵,P为任一反次Hermite矩阵, 且使A+P和A-P均为可逆矩阵, 则K=(A+P)-1(A-P)为方程(4)的解.

3 主要结果

定理1已知复数域上矩阵方程

(5)

证由于

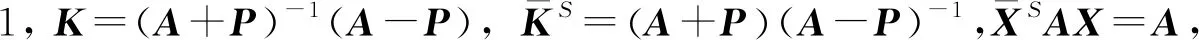
实际上，定理1的逆命题也是正确的，即有下面的结论.

定理2A为非退化的复反次Hermite矩阵,K为方程(5)的非退化解, 且E-K和(E+K)-1均为非退化矩阵, 则K=(A+P)-1(A-P), 其中P为一个次Hermite矩阵.

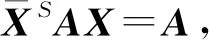
A+P=A+A(E-K)(E+K)-1=A(E+(E-K)(E+K)-1)

=A((E+K)(E+K)-1+(E-K)(E+K)-1)

=A(E+K+E-K)(E+K)-1

=2A(E+K)-1.

故A+P为非退化矩阵.又因为P=A(E-K)(E+K)-1, 易得P(E+K)=A(E-K).所以

P+PK=A-AK, (A+P)K=A-P,K=(A+P)-1(A-P).

因此K=(A+P)-1(A-P).再来证明P是一个次Hermite矩阵,由于

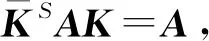
又因为

(K+E)-1(K+E)(K-E)=K-E，

(6)

且

(K+E)(K-E)=K2-E=(K-E)(K+E).

易知(6)式可变为

(K+E)-1(K-E)(K+E)=K-E，

(K+E)-1(K-E)=(K-E)(K+E)-1.

故P为次Hermite矩阵.综上所述,K=(A+P)-1(A-P), 且P为次Hermite矩阵.

下面将定理1进行推广, 给出一类特殊的反次Hermite矩阵方程的求解.

定理3已知方程

XAX=A,

(7)

设A为非退化复反次Hermite矩阵,P为任一次Hermite矩阵, 且使A+P和A-P均为可逆矩阵, 满足AP+PA=O, 则K=(A+P)-1(A-P)为方程(7)的解.

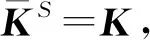
A2+AP+PA+P2=A2-AP-PA+P2,

从而有

(A+P)2=(A-P)2,

(A+P)-1(A-P)=(A+P)(A-P)-1.

(8)

根据方程(8)和定理1可得

由于定理3的逆命题也是正确的,我们有下面的定理.

定理4设A为非退化的复反次Hermite矩阵,K为方程(7)的非退化次Hermite解,E-K和(E+K)-1均为非退化矩阵, 且K=(A+P)-1(A-P)， 则有AP+PA=O.

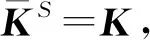
K=(A+P)-1(A-P)，

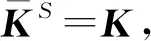
(A+P)-1(A-P)=(A+P)(A-P)-1,

化简可得

(A+P)2=(A-P)2，

即

A2+AP+PA+P2=A2-AP-PA+P2

AP+PA=O.

4 结 论

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.