r-贝尔数的对数性质
王窕窕, 熊义财, 孙 毅
(新疆大学数学与系统科学学院,乌鲁木齐 830046)
1 引 言
令Bn,r表示r-贝尔数,它最先由Corcino在文献[1]中给出,并被定义为第二类r-Stirling数Sr(n,k)的总和,第二类r-Stirling数最早由Broder 在文献[2]中引入.在组合学中,Sr(n,k) 可解释为将集合[n]∶={1,2,…,n}划分为k个非空子集的数量,使得[r]∶={1,2,…,r}中的数字分别出现在不同的子集中.之后,该组合数在文献[3]中又给出了进一步的推广.为后续方便分析,r-贝尔数可以写成如下形式:
显然,r-贝尔数在r=0时就退化为普通贝尔数,即Bn=Bn,0,其中Bn表示普通的贝尔数.
自r-贝尔数提出以来,已有一些关于r-贝尔数的研究.文献[4]研究了r-贝尔多项式的递归形式.文献[3]提出了r-贝尔数的渐进公式,并证明r-贝尔数可以用一种Dobinski的公式来表示,即
(1)
此外,文献[5]定义了一个更具一般形式的r-贝尔数,并研究了它的一些基本性质.文献[6-7]中研究了r-贝尔数的一些组合性质,其中包括它的各种递归形式以及生成函数.Mezo通过以下方式定义了r-贝尔多项式
该多项式满足以下递归恒等式[6]
Bn,r(x)=xB′n-1,r(x)+(x+r)Bn-1,r(x).
(2)

定理1[6]r-贝尔多项式的指数型生成函数为
文献[8]研究了广义贝尔多项式,其系数可以被看做是r-贝尔数的推广,并证明了这种多项式函数是凸的.但是,关于r-贝尔数的对数性质还没有人研究,本文将重点研究其对数性质.
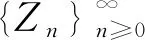
(3)
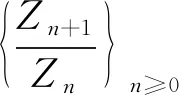
如果序列{Zn/n!}n≥0是对数凹的而序列{Zn}n≥0是对数凸的,则称实数序列{Zn}n≥0是对数平衡的,详见文献[13].
通过研究r-贝尔数的对数性质,得出了如下主要结果.
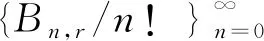
基于上述定理,还可以得出以下结果:
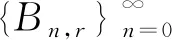
值得指出的是,文献[14]通过Bell-Touchard多项式的函数性质导出了比定理3更一般的结论,本文从组合学的角度给出了新的证明.
结合定理 2和 3可得推论1.
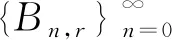
基于上述定理,使用一些不等式方法推导出定理4.
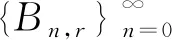
(4)
对所有的m,n≥0.注意到一个函数f∶[a,b]⊆R→(0,∞)是对数凸的,如果对于[x,y]∈[a,b]和t∈[0,1],有f(tx+(1-t)y)≤[f(x)]t[f(y)]1-t.反之,如果上式的不等号反向,则称函数f是对数凹的.众所周知,如果函数f是可导的,则称函数f是对数凸(或对数凹)的,当且仅当f′/f是递增的(或递减的).本文还考虑了函数Bx,r的对数性质,其中
(5)
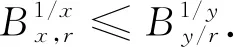
定理5当r,x≥0,以下结论成立:
(i) 函数Bx,r是对数凸的;
(ii) 函数 (Bx,r)1/x是单调递增的,即当0 定理6r-贝尔多项式只有实零点. 利用该定理可以发现,r-stirling 数关于n是对数凹的. 首先,需要一个由Bender 和Canfield得出的一个结果[15]. 引理1[15]设Z0=1,Z1,Z2,…是一组实数序列,定义 Z={Z1,Z2,…}∪{ZjZk-Zj-1Zk+1:0 则有 (n+1)pmpn-mpm-1pn+1∈[Z], 对1≤m≤n. pm-1pn+1-pmpn∈[w1,w2,…,w] (1≤m≤n). 根据引理1, Bender 和Canfield 得到了如下著名的Bender-Canfield 定理. 基于上述定理,下面给出定理2的证明. 证由定理 1, 令x=1,可得 其中ui满足 (6) 对所有的i≥2. 因此,当0≤r≤1,对所有的j≥0,有uj≥0 . 于是根据引理1,可得(n+1)Bm,rBn,r-mBm-1,rBn+1,r≥0.由此可得 据此可以得出 (7) 在式(7)中,令m=n便得证. 接下来,本文给出定理3的证明. 推论2贝尔序列{Bn}n≥0是对数凸的,且序列{Bn/n!}n≥0是对数凹的.因此,序列{Bn}n≥0是对数平衡的. 值得指出的是,推论 2的结果也以不同的方法在文献[16]中得到了证明. 证首先给出不等式(4)左边的证明,即 Bn,rBm,r≤Bn+m,r. (8) 因此可得 令B0,r=1则得到以上不等式(8). 由此可得 因此,对所有的0≤k≤m-1,有 这说明 即 这相当于,当n≥0,m≥1时,有 (9) 当B0,r=1时,显然,不等式(9)对m=0成立.因此 对n≥0,m≥0和0≤r≤2. 令不等式 (4)中的r=0,则可以得到推论3. 推论3对于贝尔数Bn (10) 对所有整数m,n≥0. E(|XY|)≤E(|X|p)1/p·E(|Y|q)1/q. 等号成立的充要条件是存在一个实数λ,使得|X|=λ|Y|或E(|X|p)=0或E(|Y|q)=0. 证先给出(i)的证明.要证(logBx,r)″≥0,即相当于证 Bx,rB″x,r-(B′x,r)2≥0. (11) 当x≥1时,利用公式 (5)可得 因此,当x≥1,可以推出 Bx,rB″x,r-(B′x,r)2 令ak=1且Bk=Xx,则对所有的整数k≥0,由引理 3,令X=Zx,Y=1且p=y/x,对所有的y>x>0,可以得出 E(Zx)≤(E|Zx|y/x)x/y(E|Y|y/(y-x))(y-x)/y=(EZy)x/y. 这相当于E(Zx)1/x≤E(Zy)1/y. 特别地,如果定理 5中的y>x>0,则不难推出 (12) 根据定理 5 和不等式(12), 易得推论4. 推论4对于r≥0的r-贝尔数,有 (13) 对于r≥0. 令RZ表示实数多项式的集合.假设{pn(x)}n≥0是 一系列标准多项式,这些多项式都是零或首系数为正的多项式,当pn(r)=0且n≥1时,如果pn(x)的阶数为n且pn-1(r)pn+1(r)<0,那么称{pn(x)}n≥0是Sturm序列.关于实根多项式的研究,可参见文献[18]. 引理4[18]令{pn(x)}n≥0是具有非负系数的多项式序列,并且 deg(pn(x))=deg(pn-1(x))+1, 其中deg(f(x))是多项式f(x)的次数.假设 pn(x)=(anx+bn)pn-1(x)+x(cnx+dn)p′n-1(x). 其中an,bn∈且cn≤0,dn≥0.则{pn(x)}是Sturm序列. 证首先贝尔多项式满足deg(Bn,r(x))=deg(Bn-1,r(x))+1.利用递归关系(2),有 Bn,r(x)=(anx+bn)Bn-1,r(x)+x(cnx+dn)B′n,r(x). 其中an=1,bn=r且cn=0,dn=1.因此,利用引理 4,可以推导出序列{Bn,r(x)}n≥0是一个Sturm 序列.因此,对于所有的r≥1,Bn,r(x)都具有实根. 根据定理 6,易得到推论5. 推论5序列{Sr(n,k)}n≥0是对数凹的,因此该序列具有单峰性. 本文对r-贝尔数的对数凸凹性进行了研究,并证明了它的一些组合性质,包括其关于n的对数凸性和对数凹性.本文还考虑了r-贝尔多项式的零点.通过使用文献[18]的结果,证明了r-贝尔多项式仅有实根.这意味着r-stirling数是对数凹的.通过计算机实验,本文还发现了一些新的猜想以供进一步研究. 猜想2对于所有r≥0,序列{Bn,r}n≥0是对数平衡的. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.2 主要结果的证明
2.1 定理2和3的证明
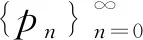


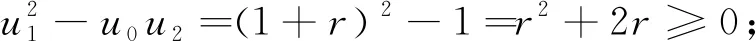


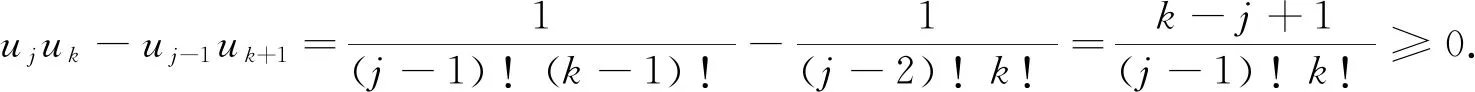
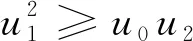
2.2 定理 4的证明

2.3 定理 5的证明
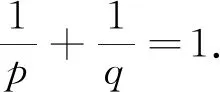

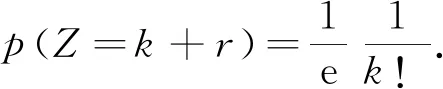
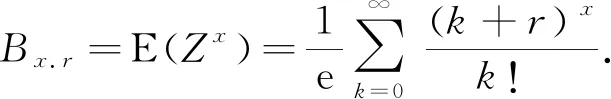

2.4 定理6的证明
3 结 论


