成败历史存档的融合龙格库塔-黏菌算法

刘宇凇，刘 升

上海工程技术大学 管理学院，上海 201600

群智能启发式算法因其工程应用[1]和人工智能[2]等多种优化领域中优秀的表现和低廉的算力要求在近十几年间愈发流行。黏菌算法[3（]slime mould algorithm，SMA）是2020 年Li 等人提出的一个用于求解随机优化问题的新算法，其由自然中黏菌的振荡模式启发而设计，通过生物振荡来传递不同位置食物信息的正向或负向反馈，从而寻找到最优的食物位置或最短路径。基本黏菌算法通过设置不同的移动方式平衡了中群智能算法中的勘探和开采阶段，同时使用了非线性自适应参数等成熟的算法改进机制，其独特的权重机制作为奖惩学习[4]的一种形式，可以为种群提供正向和负向的反馈。由此，黏菌算法具有区别于其他群智能算法的特点且依旧具有良好的可扩展性，其改进和应用受到了国外研究者广泛的关注。目前该算法已成功应用于光伏模型参数优化[5]、机器学习特征筛选[6]、医学X光图像分割[7]、计算机视觉图像阈值[8]等实际问题，在金融科技、数据挖掘、工业工程等领域具有广阔的发展前景。

然而黏菌算法依旧存在着收敛速度慢、求解精度低等问题，虽然现阶段对SMA算法的研究相对较少，国内外学者依旧使用不同的策略进行改进获得了不同的成果。文献[6]使用名为“觅食-进攻”的策略，基于贪婪策略和高斯变异，针对单个个体位置每轮迭代中进行新位置的尝试，使得求解精度大大提高；文献[7]将黏菌算法与多年来表现良好的鲸鱼优化算法[9]进行融合，在算法启动阶段使用鲸鱼优化算法进行搜索，基于其强大的全局探索能力帮助黏菌算法扩大初始搜索空间，之后使用参数控制鲸鱼优化算法停止同时启动黏菌算法；文献[8]将领导机制引入黏菌算法，通过每轮迭代选出三个候选领导个体的方式，引导整个种群向最优位置加速逼近，提高了算法的收敛性能。

基于对原始黏菌算法特点和计算细节的深入理解和分析，本文提出了成败历史存档的融合龙格库塔-黏菌算法（SFHRUN-SMA），通过添加改进的成败历史存档机制提高算法精度和速度，使用融合龙格库塔算法引导种群跳出局部最优，保持种群多样性，两种策略平衡了种群的全局和局部搜索阶段。实验中，测试了CEC2017基准测试函数，并探索了CEC2017 测试函数的高维部分，实验结果验证了改进策略对算法求解精度和鲁棒性的积极影响。

1 基本黏菌算法

黏菌算法中的黏菌一般是指多头绒泡菌，因其最初被归类为真菌，所以被命名为“黏菌”。黏菌是一种生活在寒冷潮湿地方的真核生物，黏菌的活跃动态阶段是黏菌算法研究的主要阶段。在这个阶段，黏菌使用体内的有机物寻找食物，包围它，并分泌酶来消化它。在黏菌迁移过程中，其前端会延伸成扇形，后端则连接着一个静脉网络，保证细胞质在其中流动，从而达到信息的沟通，并且根据搜寻到食物的质量和密度动态调整静脉直径的大小，最终将整个黏菌的位置调整至最优食物处。受到黏菌这种行为模式的启发，Li及其团队设计开发了黏菌算法。

基本黏菌算法的抽象数学描述如下：假设n个黏菌分布在d维搜索空间中，第t次迭代第i个黏菌的位置可以表示为Xi(t)，max_t为最大迭代次数，全局最优位置Xb表示食物位置。黏菌的觅食寻优过程分为三个阶段：

（1）接近食物

黏菌可以根据空气中的气味接近食物，下式模拟了其接近食物的过程：

其中，vb模拟了黏菌个体从种群中其他个体学习的程度，是服从[-a,a] 均匀分布的系数，vc模拟了黏菌个体对自身信息的保留程度，其从1到0线性递减，t代表当前迭代轮次，Xb代表目前为止找到食物浓度最高的个体的位置，即当前全局最优解，X代表黏菌位置，XA和XB代表两个从黏菌种群中随机抽取的个体，W代表黏菌个体的权重。

计算p的公式如下：

其中，i∈1,2,…,n，S(i)表示黏菌个体的适应度值，DF表示所有迭代轮次中找到的最优适应度。

计算vb的公式如下：

其中，a为随迭代次数减小的动态参数，用来收缩随机数vb的生成范围，以此模拟黏菌接近食物源过程中静脉逐渐收缩提高寻优精度的过程，a的计算公式如下：

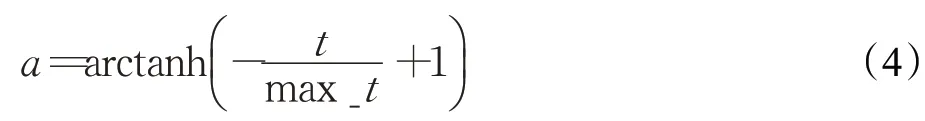
计算权重W的公式如下：

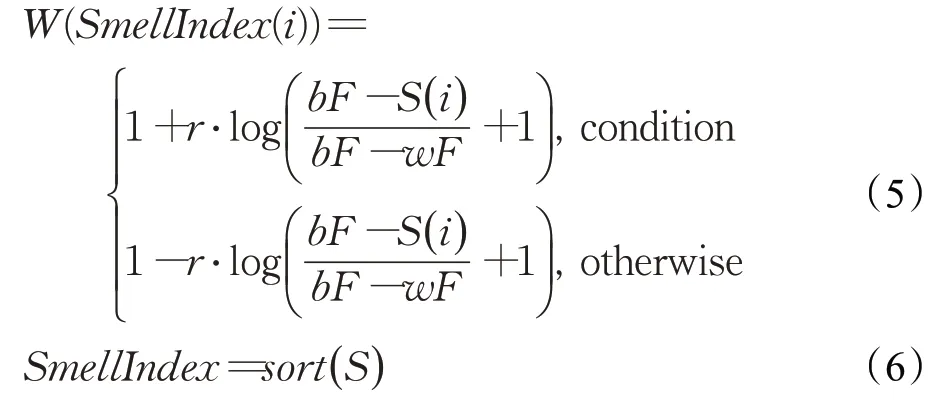
其中，选择分支的判断条件condition为适应度排名位于前一半种群，r为[0，1]间的一个随机数，max_t表示最大迭代次数，bF表示当前轮次获得的最优适应度值，相对的，wF表示当前轮次获得的最差适应度值，SmellIndex表示按照适应度值大小排序的黏菌个体索引（在求解最小值问题时使用升序排序方法）。

（2）缠绕食物

该阶段模拟了黏菌搜索食物过程中静脉结构的收缩模式，当黏菌静脉接触到的食物浓度越大，其通过生物振荡反应产生的波就越强，细胞质流动就越快，静脉细胞质粘稠程度也就越高。公式（5）描述了黏菌在搜索区域基于食物浓度或质量的判断获得的反馈，若该位置的食物浓度处于整个种群截至目前所有搜索结果的上位，则给予该位置黏菌正向反馈，反之给予下位黏菌反向反馈，以此方式充分利用适应度的计算结果信息来调整不同位置黏菌的权重，进一步调整整个种群的搜索方式。同时，随机数r保证了黏菌个体间的多样性。

基于上述理论，黏菌的位置更新公式如下：

其中，LB和UB代表了搜索空间的上下边界约束，rand和r代表了[0，1]间随机数。转换概率z在Li的参数实验中被证设置为0.03时整个算法表现最好，故本文中z同样设置为固定值0.03。

公式（7）所示黏菌算法框架通过非线性自适应参数p平衡了黏菌算法勘探和开采的不同移动方式，同时转换概率z的存在使得种群有一定概率进行自身位置的重置，有利于种群跳出局部最优，保持种群的多样性。

（3）振荡反应

黏菌依靠生物的震荡反应来调整静脉中细胞质的流动从而调整自身位置搜索最优食物位置。黏菌算法中的参数W、vb、vc用来模拟黏菌的振荡反应，W根据适应度选择不同振荡模式的行为模拟了黏菌个体根据其他位置个体搜索到的食物情况选择自身下一步行为的搜索模式，vb动态调整振荡过程中使用其他个体信息的口径模拟了黏菌静脉直径变化的过程，vc线性变化模拟了黏菌对自身历史信息保留程度的变化。

2 成败历史存档的融合龙格库塔-黏菌算法

2.1 龙格库塔算法

龙格库塔算法[10（]RUNgeKutta optimizer，RUN）是Ahmadianfa 等人提出的基于龙格库塔法数学模型进行搜索和迭代的优化算法。RUN的核心思想基于龙格库塔法的斜率计算方法，使用计算得出的斜率作为在搜索空间内进行搜索的逻辑，同时构建了一系列规则帮助种群进化迭代，形成了群智能优化算法。

2.1.1 核心搜索机制

RUN 优化算法使用四阶龙格库塔法（RK4）作为搜索框架，RK4的基本数学表示如下：

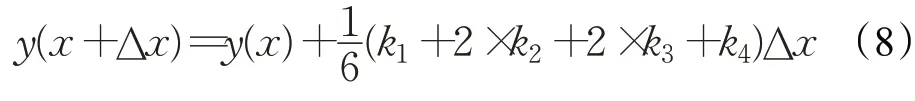
其中，权重因子k1、k2、k3和k4的数学表示如下：

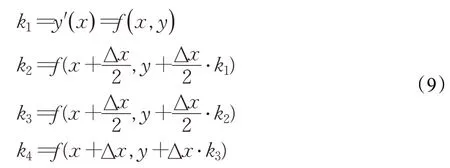
RUN算法中将种群中一个个体的位置x的两个邻居点x-Δx与x+Δx分别看作一轮迭代中该个体周围的最优的位置和最差的位置，即xb和xw。因此RK4中的k1在RUN算法中表示如下：

为了强化探索的搜索能力并创造一定随机性，上式在RUN中最终表示为：

其中：

式中，Δx由步长参数Stp确定，步长参数Stp由种群最优位置xb和种群平均位置xavg的差分确定，参数γ由解的空间大小确定，rand表示[0,1]均匀分布的随机数。由此计算出RK4中其他各项参数如下：

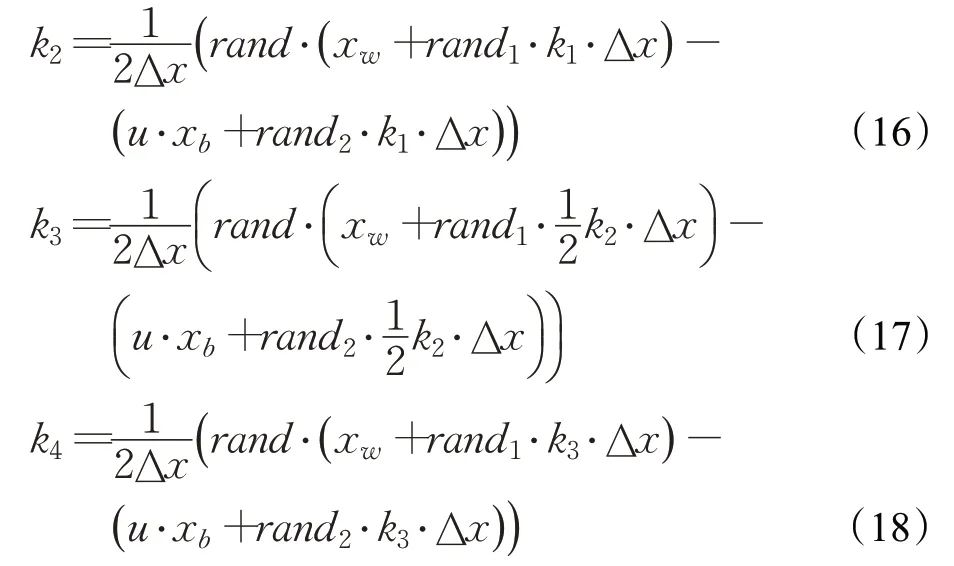
最终RUN核心搜索机制的数学表达式如下：

其中：

2.1.2 更新搜索结果

为了进一步平衡探索和开采，RUN 采用了如下的结构进行迭代间的结果更新：

其中：

2.1.3 强化解的质量

在RUN算法中，强化解的质量机制（enhanced solution quality，ESQ）被应用于增强解的质量和跳出局部最优。其过程如下：

其中，r为取值为1，0，或-1的随机数，其他参数的表示如下：

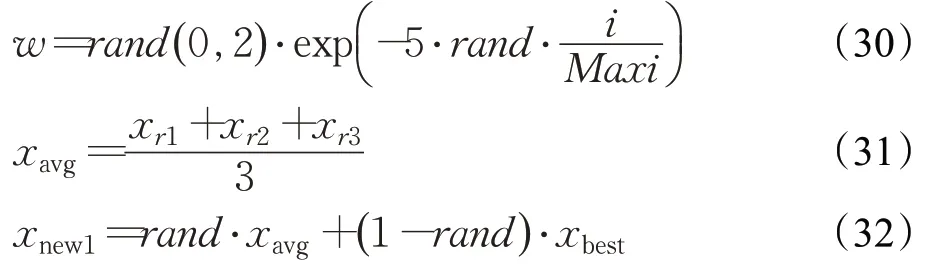
上述过程使用了大量的随机成分以及位置平均值的计算，作为龙格库塔算法基本移动后的机制，其一方面帮助成功寻优的个体强化其寻优方向获得更优，另一方面为未成功寻优的个体提供扰动，帮助种群跳出局部最优。

2.2 改进的成败历史存档机制

成功历史存档机制首次由Viktorin等人在基于成功历史的自适应差分进化算法[11（]success-history based adaptive differential evolution，SHADE）中提出，其思想来源于参数自适应的差分进化算法[12]和差分进化算法本身的框架[13]。原始的成功历史存档机制用于存储差分进化算法中的缩放因子和交叉概率两个参数，其中只有使种群适应度得到更优值的参数才会被储存，故称为成功历史存档。同时，根据每轮迭代使用不同参数更新位置后的种群适应度值变化的程度赋予成功存档中不同参数值对应的权重，最终将所有档案中参数和权重加权平均，产生下一轮迭代使用的新参数。

上述文章中证明了成功历史存档机制能够帮助算法具有更好的搜索精度和收敛效率，故本文中根据黏菌算法本身的特性和具体计算方法提出了一种改进的成败历史存档机制。首先，将原始成功历史存档存储参数信息的行为修改为存储种群个体位置信息；其次，将原始成功历史存档扩展为成功失败历史存档；最后，将种群适应度值的变化作为成功历史存档中每个位置信息被后续计算过程选取的概率值。

2.2.1 存储位置信息的成功历史存档

由上文中黏菌算法的数学表达式可知，黏菌算法中所有的参数均具有自适应的属性，且自适应方式各不相同，若继续使用成功历史存档存储黏菌算法的参数信息一定程度上会破坏黏菌算法的自适应能力。此外，黏菌算法的核心优势在于如公式（5）所示的用来表示自然界中黏菌静脉大小变化的权重计算过程，但若种群中没有优质的个体位置信息或具有优质位置信息的个体较少的情况，权重计算过程会失效，最终导致黏菌算法的精度提升出现瓶颈。

因此，本文提出了一种存储位置信息的成功历史存档S_Archive，即个体在搜索过程中若得到比自身当前适应度更好的适应度，则新的位置会被记录在成功历史存档中。设置一个参数S_Archive_N用来限定成功历史存档的容量，若成功历史存档存储的位置信息达到容量上限，则从存档的起始位置依次更新存储的位置信息。

2.2.2 成功失败历史存档

原始的黏菌算法中，最基础的位置移动方式如公式（1）所示，其中，XA和XB代表两个从黏菌种群中随机抽取的个体，因此公式（1）中(W·XA(t)-XB(t))部分并不能确定个体移动的方向是向更优位置移动还是向更差位置移动，加之取值可正可负的表示随机步长的参数vb后，使得黏菌算法最基本的搜索方式随机程度较大，缺乏一定的方向性。

因此，本文扩展了上述的成功历史存档机制，提出了一种存储位置信息的成败历史存档。构建失败历史存档F_Archive，个体在搜索过程中若得到比自身当前适应度更差的适应度，则新的位置会被记录在失败历史存档中。构建成功历史存档和失败存档后，将原始黏菌算法公式（1）中XA和XB替换为XA_S和XB_F，即一个从成功历史存档中随机选取的位置和一个从失败历史存档中随机选取的位置。公式（1）则改写为：

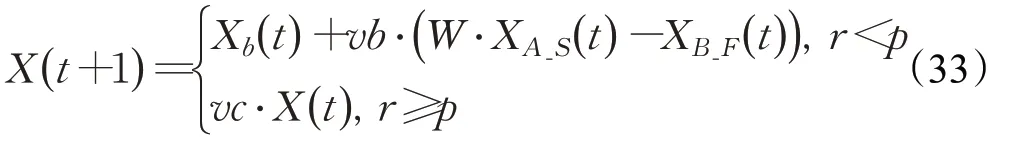
此时，若vb的值取到正数，黏菌个体的基本移动行为确定为从失败历史位置向成功历史位置移动的方向；若vb的值取到负数，则基本移动可以视为具有一定程度的反向学习特征，扩大种群的搜索空间，保持种群的多样性。

传统的反向学习策略或其他新位置生成策略都需要计算新位置的适应度，增加了算法的复杂度，在目标函数复杂的现实问题中，该类策略运行的效率会大打折扣。上述成败历史存档机制不同于反向学习等学习策略，无需增加种群个体位置适应度的计算过程，仅为更新的位置信息添加了“成功”或“失败”的标签，节约运算时间的同时，赋予种群个体移动时一定的方向，加快种群的收敛速度。

通过分析可以发现，高校自主招生与高考统一招生对人才的选拔与评价模式有所不同，有其自身明确的特征。如自主招生与高考招生的评价方面不同，自主招生是从德智体三方面评价学生的，更加全面化，而高考招生考察较为单一，只针对学生的“智”，即是学习成绩进行考察。自主招生与高考招生选拔标准化不同，自主招生选拔人才更加尊重学生的个性发展与个性化差异，重视学科专长突出的学生，而高考招生考察多科目，从综合成绩评价学生。同时，自主招生注重学生的综合素质与人格发展，而高考主要是从成绩评价学生。

2.2.3 作为概率的适应度变化值

原始的成功历史存档机制中，将适应度值的变化量作为存档中参数的权重，最后通过加权平均得到新的参数。文献[14]指出，在存档中使用普通算术平均会使最终结果收敛至一个很小的取值范围内，由此提出了使用加权平均计算平均值，其中权重为种群适应度的变化值。此后，使用适应度变化值作为评价学习结果重要程度的机制被保留并使用于多种基于存档的改进算法中。受此启发，本文中同样使用成功历史存档S_Archive保存个体在移动中适应度值的变化量，不同的是将该变化量作为该位置之后被选取的概率，即XA_S的选取过程不再服从均匀分布，而是服从不同适应度值变化量的分布，得到更大适应度值提升的位置更有可能被选取，得到较小适应度值提升的位置则被选取的可能性较小。该过程首先保证了所有位置并没有通过任何运算进行改变，即保留了黏菌算法从种群中其他个体获取信息的特点；其次使对种群适应度提升较大的成功位置更有机会引导其他种群个体；最后使用概率的方式使对种群适应度提升较小的个体依旧有机会被选取，保证了种群的多样性，同时一定程度上避免了种群陷入局部最优。

上述概率值的机制仅使用在成功历史存档中，而不使用在失败历史存档中。因为失败历史记录的适应度值变得更差的变化量无助于确定未来更优的搜索方向，若从旧位置更新到新位置后适应度变差的值很大，将该变化值作为概率后，只能帮助个体从更差位置移动向较优位置，而个体从次优位置移动向更优位置才是算法不断迭代的目的。

2.3 自定义的长短结合交流时机

本文采用并行计算-信息交流的机制将上述龙格库塔算法与成败历史存档机制改进的黏菌算法进行融合。经过大量实验发现，频繁的信息交流会严重损失两算法各自的特性和按照迭代轮次积累的自适应参数的价值，时间间隔较长的信息交流则会出现某一算法始终优于另一算法的情况，融合过程变得冗余。

本文通过大量实验比较分析，提出了一种自定义的长短时间间隔结合的交流时机，用来确定两个种群什么时候交流，具体交流时机如图1所示。

图1 自定义的长短时间间隔结合的交流时机示意图Fig.1 Customized long-short interval timing of communication

其中根据最大迭代轮次，前五分之一视为短期，将其均匀分割为五等份，每份结尾进行交流；中间五分之二视为中期，将其进行两次黄金分割后，每份结尾进行交流；最后五分之二视为后期，不进行交流。以最大迭代次数500 为例，交流时机的取值则为[20，40，60，80，100，129，176，223，300]。

2.4 基于空间移动的信息交流机制

传统的多种群信息交流多为最优位置或整个种群的直接替换。在龙格库塔算法中，个体移动过程使用了种群位置的平均值、最优值等；在黏菌算法中，个体移动过程的权重使用了所有个体的位置和最优位置，若按传统方法进行信息交流，一定程度上会损失两算法各自的搜索特点和计算优势。

因此，本文受Jafari 等人[15]融合粒子群算法和文化算法的工作启发，提出了基于空间移动的信息交流机制。实验中发现，龙格库塔算法在高精度求解空间中表现优秀，但整体求解过程方差巨大，极易陷入局部最优，导致迭代的停滞；黏菌算法稳定性较好，但缺乏在高精度空间进一步提升的潜力。故本文中将龙格库塔算法作为辅助算法，改进的黏菌算法作为主体算法，将龙格库塔算法的最优位置和改进黏菌算法的成败历史档案构成的空间作为信息交流的两个主体。

首先，将龙格库塔算法的种群规模设置为改进黏菌算法的一半，放大基本移动中种群受最优位置的影响，减弱种群受平均位置影响的不稳定性，同时减少双种群融合的运算开销。其次，将成败历史存档作为参与信息交流的空间主体，有助于保留黏菌算法本身的位置信息和相关参数的有效性，移动后的成败历史存档可以更好地引导黏菌算法进行位置更新。再次，划分最优位置和位置空间之间的相对关系。最后，根据每种相对关系构建一系列基于空间移动的信息交流模式，实现种群间信息有效的交流。信息交流的过程如下所示：

当改进的黏菌算法最优适应度优于龙格库塔算法时：若龙格库塔算法的最优位置处于黏菌算法目前的种群空间中，将龙格库塔算法最优位置的值赋予失败历史存档，加速黏菌算法向更优空间的移动；若龙格库塔算法的最优位置不处于黏菌算法目前的种群空间中，说明龙格库塔算法目前的最优位置信息质量较差，将其替换为黏菌算法的最优位置。当龙格库塔算法最优适应度优于改进的黏菌算法时：若龙格库塔算法的最优位置处于黏菌算法目前的种群空间中，说明当前搜索范围有效但不够精确，将成败历史存档同时向龙格库塔算法最优位置移动；若龙格库塔算法的最优位置不处于黏菌算法目前的种群空间中，说明成败历史存档已完全落后于龙格库塔算法，将成功历史存档降级为失败历史存档，同时将龙格库塔算法最优位置赋予黏菌算法，引导主算法进行跃进。

2.5 成败历史存档的融合龙格库塔-黏菌算法

本文提出了成败历史存档的融合龙格库塔-黏菌算法（success fail history based hybrid RUNgeKutta optimizer and slime mould algorithm，SFHRUN-SMA）。首先，提出了改进的成败历史机制，设置成功失败历史存档存储位置信息，适应度的变化量作为成功存档中的概率，将该机制加入原始黏菌算法，有效地将黏菌算法的基础移动方向调整为“成功”到“失败”，加速黏菌算法的启动；其次，引入龙格库塔算法作为辅助算法，将其种群规模设置为黏菌算法的一半，使用并经计算-信息交流的模式将其和改进后的黏菌算法进行融合；再次，自定义了两种群交流的时机，实现了两算法各自运算特点的保留；最后，基于空间移动，提出了一系列按不同情况进行不同行为的信息交流方式，使得作为辅助算法的半种群规模龙格库塔算法调整速度更快，同时间接的交流调整方式使得作为主算法的全种群规模黏菌算法的调整更为精准和谨慎。

通过文献和实验可知，黏菌算法最大的优势是其稳定性，但其随机程度较大的勘探阶段移动方式和较为简单的开采阶段移动方式导致了其启动较慢和后期求解精度不足的缺陷。改进的成败历史存档机制可以帮助黏菌算法在前期的勘探中更具方向性。龙格库塔算法的辅助可以帮助黏菌算法在后期的开采中更具潜力，同时两算法融合后，黏菌算法稳定的表现可以引导龙格库塔算法规避陷入不稳定的波动中，龙格库塔算法高精度的求解潜力可以引导黏菌算法更加精细地获得最优解。分别基于群智能技术和数学方法设计的两算法相辅相成，融合后可以成为既适合大规模低精度问题又适合小规模高精度问题的综合算法。此外，改进的成败历史存档可以作为两算法融合后交流的桥梁，规避传统交流方法导致的多种群信息部分损失的缺陷，同时更加高效地按照具体情况对不同种群的信息进行调整实现了多种策略间有机地结合。

在黏菌算法框架中，转换概率可以使个体小概率地进行自身位置的重置；在龙格库塔算法框架中，强化解的质量机制可以为未成功寻优个体提供扰动；在改进的成败历史存档机制中，作为概率的适应度变化值保证了个体小概率偏离当前局部最优方向的可能。故本文算法在局部最优跳出问题上具有一定的对策，且相较于传统的多种分布随机扰动的方法，本文算法局部最优跳出方法更加与算法本身、改进机制本身相匹配，所需的适应度函数计算计算次数更少。综上所述，融合了两算法各自的计算优势，同时弥补了两算法存在的缺陷，使算法的求解精度和鲁棒性得到提升。

2.6 改进算法的步骤

SFHRUN-SMA算法的流程图如图2所示。

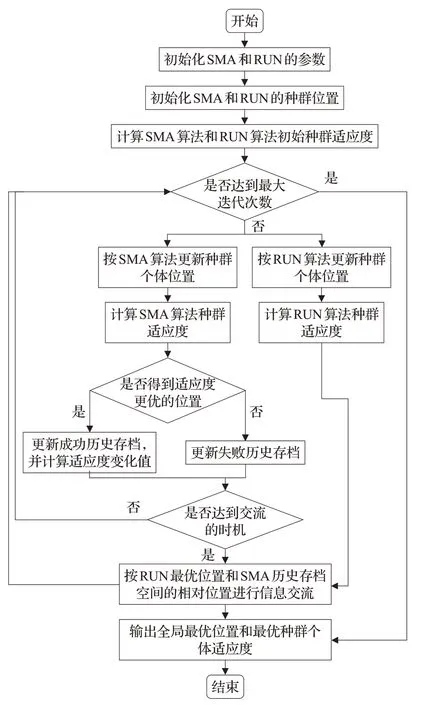
图2 SFHRUN-SMA算法流程图Fig.2 Flow chart of SFHRUN-SMA

2.7 时间复杂度分析

假设种群规模为N，搜索空间维度为D，最大迭代次数为T，原始SMA 算法的时间复杂度主要来源于初始化、适应度计算和位置更新，其时间复杂度为：O(N)+O(N·T)+O(N·D·T)。原始RUN 算法的时间复杂度与上式相同。SFHRUN-SMA算法主要由成败历史存档机制和融合龙格库塔算法两个改进策略组成，由于作为辅助算法的龙格库塔算法在前述中设置为黏菌算法种群规模的一半，则本算法全种群初始化过程的时间复杂度为O(N+0.5N)。同时，成败历史存档机制并不需要增加个体适应度计算的过程，故计算个体适应度的时间复杂度为O( (N+0.5N)·T)。在位置更新过程中，按照作为概率的适应度值变化量选取个体位置的过程需要对成败存档中个体进行排序，并随机选取一个位置参与计算，该过程时间复杂度为O( 0.5N·lg( 0.5N)·T)。综上所述，SFHRUN-SMA 的时间复杂度为：O(N·(1.5+(1.5+0.5 lg( 0.5N)+1.5D)·T))。

在维度更高、适应度函数计算更为复杂的实际工程优化问题中，本文算法相较于传统反向学习改进的算法和使用贪婪策略的其他算法具有更少的适应度函数计算次数，整体的时间复杂度与其相当甚至更低，因此在实际的工程应用问题中是可行的。

3 仿真实验及结果分析

实验环境为Windows10，64 位操作系统，CPU 为Inter Core i7-6700HQ，主频2.6 GHz，内存8 GB，算法基于MATLAB2020b编写。

实验1为了充分验证本文所提出的SFHRUNSMA 在求解函数优化问题时的求解精度和鲁棒性，将SFHRUN-SMA 算法与其他算法在CEC2017 测试函数上进行求解，并进行实验结果的对比。对比用算法包括最新的改进黏菌算法AFSMA[6]、原始的黏菌算法SMA[1]、同一科研团队提出的哈里斯鹰算法HHO[16]、近几年表现优秀的正余弦算法SCA[17]和经典的鲸鱼优化算法WOA[9]。

为保证每种算法对比时的公平性，实验中种群规模设置为30，最大迭代次数设置为500，并独立运行30 次计算得出统计结果。对比用算法参数设置均来源于对应文献设置，如表1 所示。其中SFHRUN-SMA 算法的成败历史存档规模分别设置为种群规模的一半，即15。

表1 主要参数Table 1 Main parameters

本文选用了表2 所列示的29 个CEC2017 基准测试函数，其类型包含单峰（unimodal，UM）、多峰（multimodal，MM）、混合（hybrid，H）及复合（composition，C），维度可选用10、30、50、100，此处实验使用标准维度30维，02号函数由于高维的不稳定性习惯上不使用。

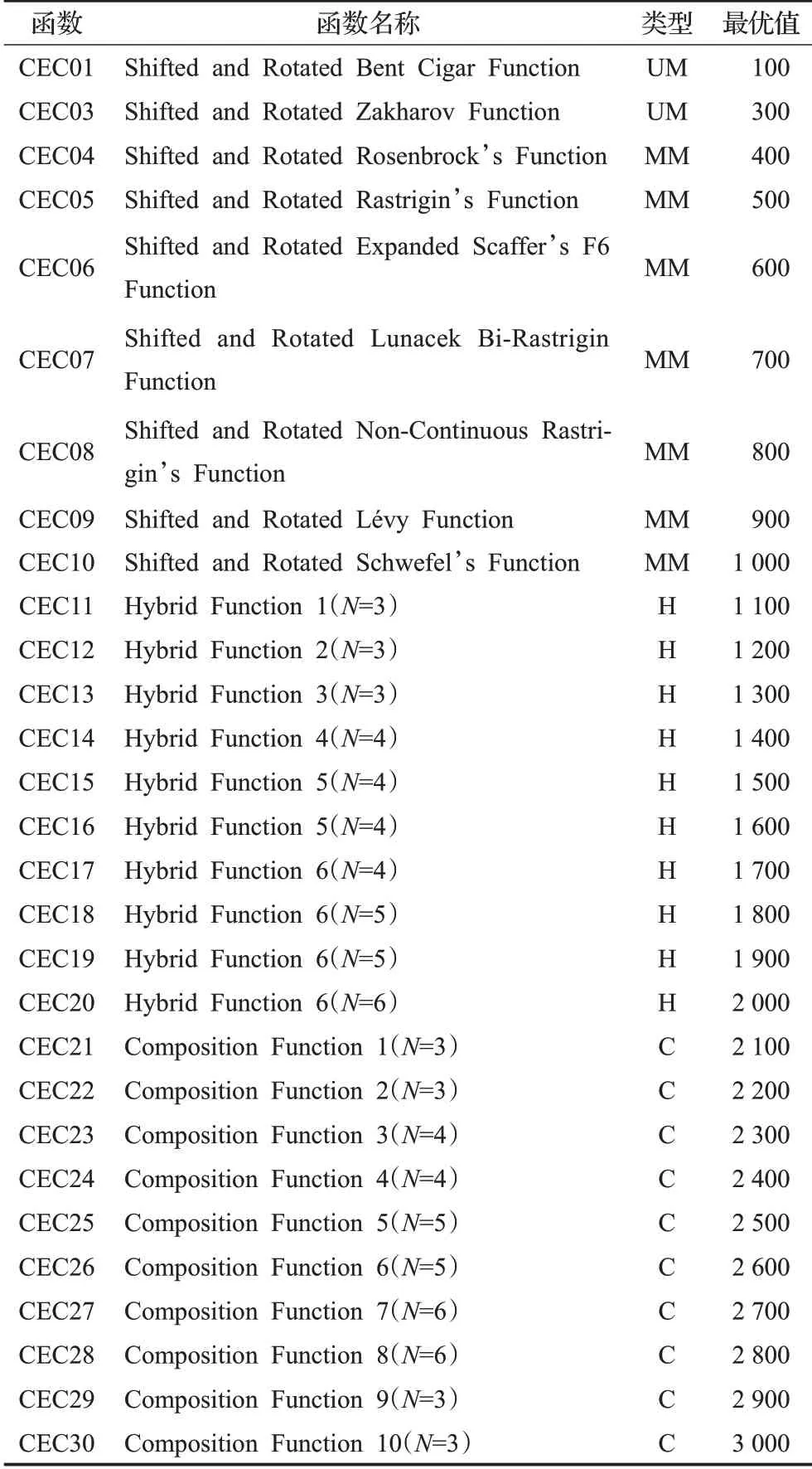
表2 CEC2017函数Table 2 CEC2017 function

表3为SFHRUN-SMA与第一部分算法进行对比的实验结果。总体上看，SFHRUN-SMA在29个CEC2017基准测试函数中在23个函数上平均求解精度的表现优于其他所有对比算法，另外6 个测试函数上均由原始SMA算法取得更优，但在此基础上SFHRUN-SMA算法的求解精度均高于改进算法AFSMA，针对更复杂的、更接近现实的问题SFHRUN-SMA 具有更好的求解精度和收敛速度。

为了进一步验证改进算法的有效性，需要对群智能算法结果进行统计检验[18]，本文选择Wilcoxon 秩和检验进行统计检验，显著性水平设置为5%，表3展示了SFHRUN-SMA 算法与其他五种算法的检验结果，每列最后一个符号为SFHRUN-SMA 分别与五种算法成对比较结果的胜负标记，其中“+”代表优于比较算法，“-”代表劣于比较算法，最后一行为优于和劣于的函数数量合计。表3 结果表明SFHRUN-SMA 算法对于每个CEC2017 基准测试函数的求解结果对于SCA、HHO、WOA三个对比算法分布完全不同，可以证明SFHRUNSMA算法的求解精度明显优于该三种算法。相较于改进算法AFSMA，SFHRUN-SMA算法在三分之二的测试函数上分布不同，并且整体求解精度优于AFSMA，可以证明改进策略对算法求解精度的提升有显著的影响。相较于原始SMA，接近半数的测试函数结果分布无法证明有明显差异，分析可知SFHRUN-SMA 算法尽可能地保留了原始SMA 算法动态权重、自适应转换概率等优点，故分布并未出现明显差异，但同样的在求解精度上有较大提升，可以证明SFHRUN-SMA在求解CEC2017基准测试函数上表现更优。

表3 CEC2017测试函数和Wilcoxon秩和检验的结果对比Table 3 Comparison of CEC2017 function results and Wilcoxon’s rank-sumtest

为了形象地观察改进算法的收敛性能，对SFHRUNSMA与AFSMA、SMA、SCA、HHO、WOA进行收敛性分析。图3给出部分基准测试函数的收敛曲线图，各算法曲线图例与图3（f）一致。为了便于观察高精度的曲线收敛情况，纵坐标取以10 为底的对数绘制所有曲线图像。观察可得，SFHRUN-SMA 算法在迭代前中期展现出和原始SMA 类似但效果更好的寻优线路，说明了成败历史存档机制在保留了SMA原本的特点和优点的基础上加快了SMA 算法的收敛速度。同时，在迭代中后期得益于RUN 算法的引导SFHRUN-SMA 算法可以执行更为精细化的搜索，保证了整体算法搜索到更优解的潜力。直观来看，本文改进策略的组合对算法的收敛速度和局部最优的跳出有积极影响。

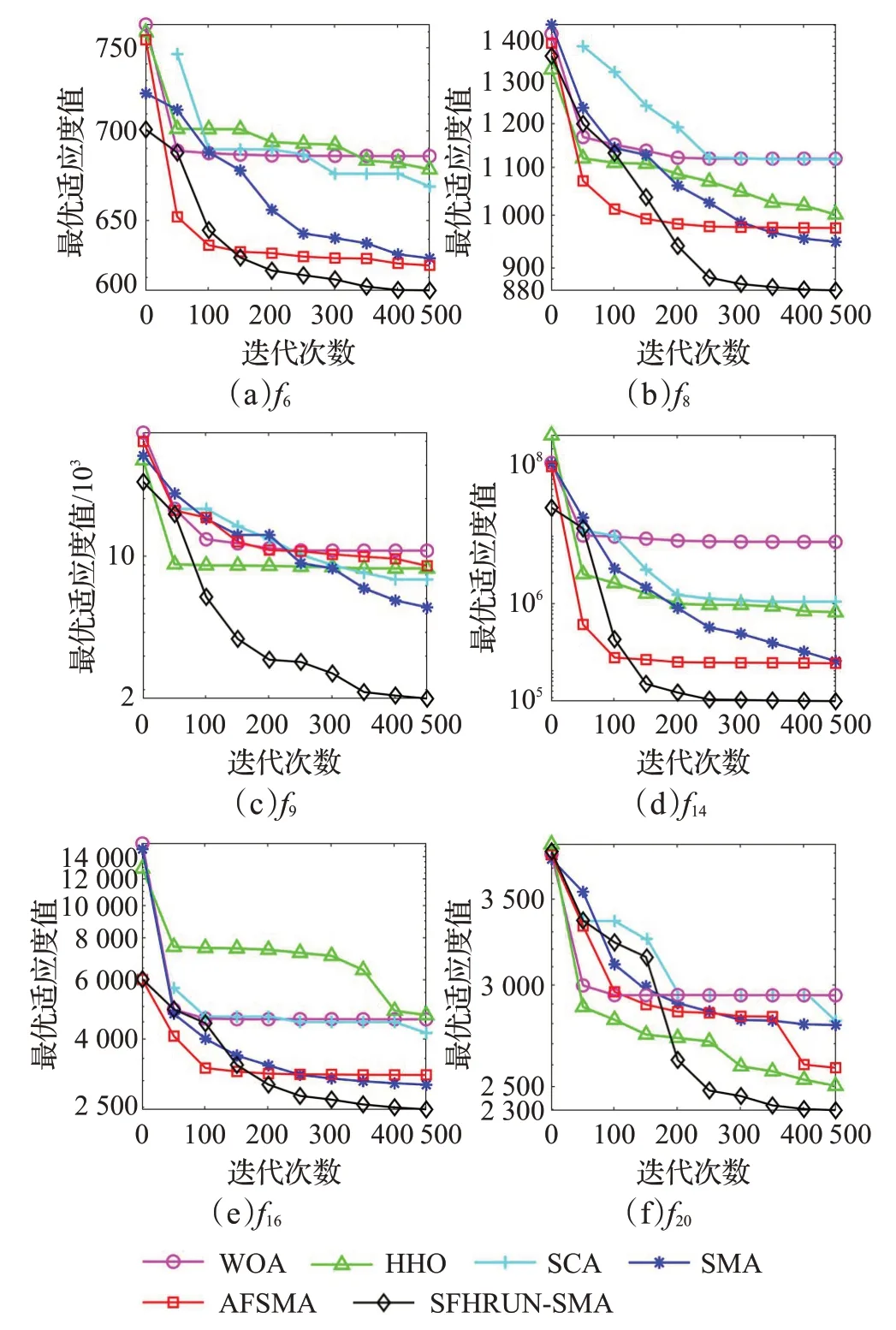
图3 CEC2017测试函数收敛曲线Fig.3 CEC2017 Function average convergence curve

为了综合地评估SFHRUN-SMA 与其他算法对比的竞争性，使用平均绝对误差MAE 对上述算法进行排序[19]。表4 展示了所有算法基于29 个CEC2017 基准测试函数的MAE。MAE计算公式如下：

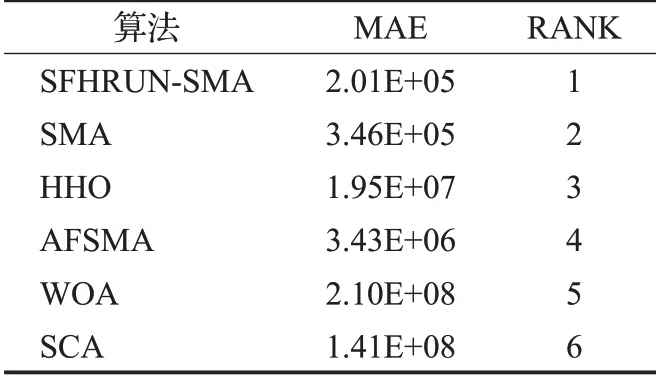
表4 MAE算法排名Table 4 MAE algorithm ranking

其中，NF为函数个数，fi为算法在第i个函数上求解结果的平均值，fi*为第i个函数的理论最优值。

由表5可知，SFHRUN-SMA排名第一，原始算法SMA排名第二。并且SFHRUN-SMA 的MAE 值明显小于其他算法，更加综合地表明了该算法的有效性和鲁棒性。

实验2 随着测试函数搜索维度的升高，最优值的求解困难程度也随之升高，求解高维问题有助于让基准测试函数的求解难度更加接近于现实中复杂的问题，以此可以间接检验算法应用于现实问题中的表现。使用CEC2017基准测试函数，搜索维度设置为50和100两个高维进行实验，表5展示了实验结果。由表5可知，当维数上升至50维后，SFHRUN-SMA在22个测试函数上求解精度占优，改进算法AFSMA在4个测试函数上占优，原始SMA 在3 个测试函数上占优；当维数上升至CEC2017 测试函数设置的最大维数时，SFHRUN-SMA在22个测试函数上占优，改进算法AFSMA在4个测试函数上占优，原始算法SMA 在2 个测试函数上占优，HHO算法在1个测试函数上占优。可以说明，在高维环境下SFHRUN-SMA 的改进策略依旧有效，从成败历史存档和RUN算法的引导大大加速了高维空间中算法的启动速度，从而更快地收缩搜索空间，为精细搜索创造先机，相对于对比算法有着更强的稳定性和鲁棒性。

表5 高维CEC2017测试函数的结果对比Table 5 Comparison of high dimension CEC2017 test function results

实验3 为了验证SFHRUN-SMA 算法改进的有效性，需要对比分析不完全算法[20]，使用CEC2017基准测试函数进行SFHRUN-SMA 与其不完全算法SFHSMA 与RUN进行对比，表6展示了更加综合和直观的MAE排名结果。由表6可见，SFHRUN-SMA算法在所有维度上均取得第1，且在100维度上优势更加明显，因此SFHRUNSMA在求解问题普遍的适用性上强于两个不完全算法。

表6 MAE不完全算法排名Table 6 MAE incomplete algorithm ranking

SFHSMA在较低维度最终的求解效果与原始SMA相似，分析可知单纯的成败历史存档并不能为种群带来不同于原始种群位置信息的新知识，固表现与原始SMA相似。同时，SFHSMA 在100 维度求解精度高于RUN，由此可知成败历史存档机制加强了SMA算法在更高维度中的稳定性。RUN 算法在低维的求解精度较高，但在高维缺乏稳定性，将其与SFHSMA 融合构成本文算法后，SFHRUN-SMA 在三类维度中表现均超过独立的SFHSMA 和RUN。一方面说明作为辅助算法的RUN成功地对SFHSMA 起到了引导作用，帮助其在各个维度取得更优结果，另一方面说明SFHSMA 帮助RUN 规避了求解不稳定的缺陷。此外，SFHRUN-SMA的MAE结果与排名第2的算法差距较大，侧面说明了本文构建的两种群交流机制在实现交流的基础上对整体算法精度的提升也有一定贡献。综上，两种改进策略及相关交流策略的结合有利于本文算法有效性和鲁棒性的提升。

4 结束语

针对SMA 算法存在的不足，本文使用了改进的成败历史存档机制和融合龙格库塔算法两个策略对原始SMA进行改进，提出了成败历史存档的融合龙格库塔-黏菌算法SFHRUN-SMA，并将该算法应用于CEC2017测试函数进行求解。改进的成败历史存档机制通过对成功失败位置信息的存储并将适应度的变化值作为概率赋予每个位置信息，提高了原始黏菌算法逼近最优解的启动速度，对不同特点的测试函数具有普遍适用性，且该机制具有一定的可迁移性；迭代过程中，将种群规模为SMA一半的RUN算法作为辅助算法，并定制了一系列两种群间交流的机制，保留两算法优势的同时弥补

两算法的固有缺陷，利用RUN 更强的深度求解潜力引导SMA，利用SMA更稳定的求解路径平衡RUN多次重复求解的方差，在保证种群多样性的前提下提高算法求解精度。此外，为了多维度综合地评估改进算法的有效性和同其他算法相比的竞争力，本文使用了MAE、Wilcoxon秩和检验等指标，同时对CEC2017基准测试函数的高维进行探索和测试，多角度地证明了本文所提出算法的求解精度和鲁棒性。

在未来的研究中，希望对黏菌算法进行进一步的改进和测试，提高该算法针对更多样、更复杂问题的适用性，并将其应用于金融科技和数据挖掘等领域，进一步落实群智能算法的实际应用。