风沙地区低净空桥梁下部流场结构及积沙特征分析

师景瑞,石 龙

(1.甘肃综合铁道工程承包有限公司,兰州 730030； 2.西南交通大学土木工程学院,成都 610031； 3.中铁西北科学研究院有限公司,兰州 730030)

风沙流是气流携带沙粒运动的一种气固两项流，也是形成风沙灾害的主要原因。中国是世界上遭受风沙灾害最严重的国家之一[1]，多个行业每年因此损失数上亿元，尤其铁路行业，轻则污染道床增加养护费用，重则堵塞桥涵，甚至引起列车出脱轨[2]。

为减轻风沙灾害对铁路的影响，保障铁路的安全运行，国内外学者通过理论分析、数值模拟、风洞试验和现场监测等手段开展了大量的相关研究，涉及的内容主要包括风沙流特征[3-6]、防沙工程优化与效益评价[7-13]、铁路工程结构沙害形成机理[14-18]、风沙灾害风险性评估[19-20]、风沙荷载计算[21]等。然而，关于桥梁风沙灾害的研究成果却很少，忽视了风沙灾害对桥梁的影响。王奭等[22]通过现场调研和数值模拟，探讨了格库铁路青海段桥梁沙害成因，遗憾的是该研究采用纯气流场分析积沙形成机理，实际上风沙流属于典型的气固流，采用两相流模拟更加合理。此外，该文献中的桥梁净空较高，一般对风沙流的扰动能力较弱，中间梁体下方产生积沙的可能性非常小，积沙通常集中在气流扰动强烈的路桥过渡段，这也在该研究的现场调查中得到证实。然而，低净空桥梁积沙与上述研究存在差异，积沙不仅发生在路桥过渡段，还可能发生在中间梁体正下方。例如，李良英等[23]研究成果中的青藏铁路巴索曲特大桥就属于低净空桥梁，积沙几乎堵塞梁底。该研究依然采用纯气流场预测桥下积沙的可能性，无法直观地反映桥下积沙演化规律，故存在一定片面性。

鉴于此，基于计算流体力学软件，构建欧拉双流体非稳态模型，结合现场实测数据，剖析低净空桥梁周围的风沙流场演化规律，揭示其沙害形成机理，并提出相关建议，以期为类似地区工程建设提供参考。

1 现场测试

本次测试地点位于风沙地区某低净空桥梁处，梁体类型为T梁，梁底净空约3.0 m。监测设备主要为风杯式风速风向仪，具体参数如下：风速传感器的起动风速约0.5 m/s，风速监测范围为0～50 m/s，精度±0.1 m/s；风向传感器的量程在0～360°之间，精度±5°。测试高度距地表0.8 m，风况监测时间约为1.0 h，取其2 min的平均值作为该点的监测风速值。为保证数据的即时性，在风况监测期间，同时布设7套风速传感器，测点布置如图1所示。

图1 桥梁风况监测点布置(单位：m)

2 数学模型

2.1 几何模型

几何模型的尺寸影响着数值结果的准确性，模型尺寸太大对计算机的性能要求较高，相应的大幅度增加计算时间，尺寸太小可能使得梁体背风侧的涡流区与出口边界相交，从而影响计算结果的精度。为提高计算精度并减少计算量，通过多次试算确定出较为合理的模型尺寸：长90 m、宽20 m。此外，在风沙地区，现有桥梁大多采用T梁，故本次研究以T梁为主，仅在研究梁体类型对流场结构和积沙形态对比时，建立了箱梁模型。考虑到按照实际梁体的几何形状建模，很难得到高质量的网格，故在几何建模过程中简化了梁体的几何形状。

2.2 网格划分及边界条件

对计算域进行非结构自动化网格划分，网格划分类型Quadrilateral Grids，近壁区域采用壁面函数法进行处理，各工况下的网格单元总数均超过60万个。模型的边界条件见表1。

表1 模型边界条件

2.3 控制方程

在模拟过程中需要求解质量方程和动量方程，其表达式分别见式(1)～式(3)。

质量方程

(1)

动量方程

气相

-γ1∇p+∇·τ1+γ1ρ1g+F12(v1-v2)

(2)

固相

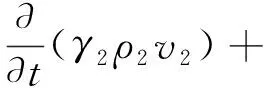
-γ2∇p-∇p2+∇·τ2+γ2ρ2g+F21(v2-v1)

(3)

式中，当m=1、2时分别代表气相、固相；vm、τm和ρm分别为m相的速度、应力应变张量和密度；γm为第m相的体积分数，且满足γ1+γ2=1；p和p2分别为气固两相的共享压力和固相的压力，g为重力加速度；F12=F21为气相和固相的动量交换系数。

2.4 计算参数

采用计算流体力学软件中的欧拉双流体非稳定模型对风沙流的运动特征进行模拟，其中，将气相设置为主相，沙粒设置为稀相，密度分别取1.225 kg/m3和2 600 kg/m3，初始沙粒体积分数取为2%，沙粒平均粒径取为0.125 mm，且假设其为球体。现场测试时间段的平均风速约为14.2 m/s，为保持两者一致性，数值模拟时入口风速也取为该风速值。

3 结果分析

3.1 数值结果与现场测试结果对比

图2为梁底净空3.0 m时数值模拟和现场测试的相对风速(来流风速/测点风速)对比，可以观察到两种结果的变化趋势基本吻合，说明所建模型能较好地模拟梁体周围的风速变化特征。值得注意的是，总体上数值模拟结果略高于现场测试结果，主要原因可能是所建模型计算域的高度是有限的，而现场实际在高度方向上是无限的，数值模拟中或多或少存在一定的阻塞效应。另外，梁体几何模型的简化也是产生上述差异的原因。

注：距离的负值代表在梁体中线迎风侧，正值代表在梁体中线背风侧，下同。图2 数值模拟与现场测试结果对比

3.2 T梁体周围流场及积沙分布特征

图3为T梁底不同高度处相对风速曲线。从图3可以看到，不同高度处相对风速变化趋势基本一致，曲线近似对称于梁体中心。为便于归纳总结，以梁体为分界线将曲线划分为3部分：①梁体迎风侧附近的相对风速呈“先减小后增大”趋势，谷值在-4h处，相对风速在1.0以下；②梁体范围内的相对风速近似呈“M”形分布，峰值和谷值分别在腹板和梁体中线处，相对风速均大于1.0；③梁体背风侧附近的相对风速呈“先减小后增大”趋势，谷值在4h处，相对风速基本在1.0以下。上述现象表明，梁体迎风侧和背风侧的风速发生了明显衰减(分别是梁体阻碍作用和气流扩散作用所致)，而梁体正下方的风速得到了加强(主要是过流断面被压缩引起的“狭管效应”所致)。

注：L为距梁体中线的距离；h为梁下净空；H为距地表的距离，下同。图3 T梁梁底不同高度处相对风速曲线

图4为T梁周围的气流流线，不难发现，梁体两侧一定范围之外(梁体两侧5h范围外)未扰动的气流流线近似平行于地表，扰动后气流流线改变了方向，在梁底正下方的上层流线向梁顶发生了明显的弯曲现象。

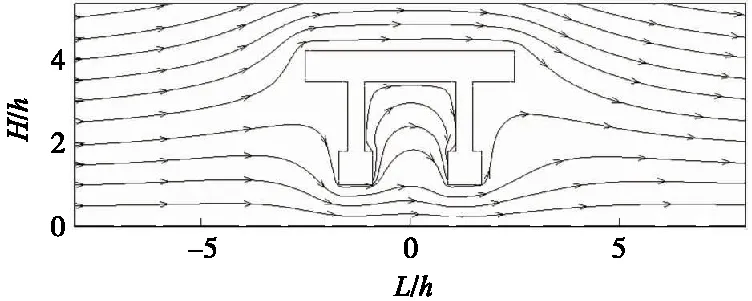
图4 T梁周围气流流线

图5为t=2 000 s时的沙相体积分布云图，很明显积沙主要集中在梁体迎风侧、背风侧，这种积沙形态主要与梁体周围的流场结构密切相关。气流相对风速表明梁体迎风侧、背风侧和正下方的风速分别发生衰减和加强，相应地气流的携沙能力就会降低和增强，致使这些区域的风沙流分别处于风积和风蚀状态，从而产生沙粒堆积和地表风蚀现象。值得注意的是，腹板间正下方的风蚀区也出现了沙粒堆积，这与相对风速的分析结果相矛盾，其主要原因是腹板间的气流方向并非平行于地表，而是出现了绕流现象，部分质量较轻的沙粒就会随着气流运动，使其与梁体碰撞而跌落在腹板间正下方。此外，梁底周围逐渐增多的积沙改变流场结构，也是影响梁底积沙的原因。

注：风向从左到右。图5 t=2 000 s时T梁周围的沙相体积分布云图

图6为某低净空桥梁(h≈1.0 m)现场积沙以及其提取的两桥墩中间的积沙剖面，可以观察到积沙形态及分布与数值模拟结果(图5)基本吻合，说明所建数学模型能够较好地反映梁体周围的积沙演化特征。此外，注意到实际工程中桥梁背风侧与迎风侧的积沙量相当，这与数值模拟结果存在差异，主要原因在于现场积沙是桥梁两侧多个风向综合作用的结果，而数值模拟结果仅仅是单一风向作用的结果。

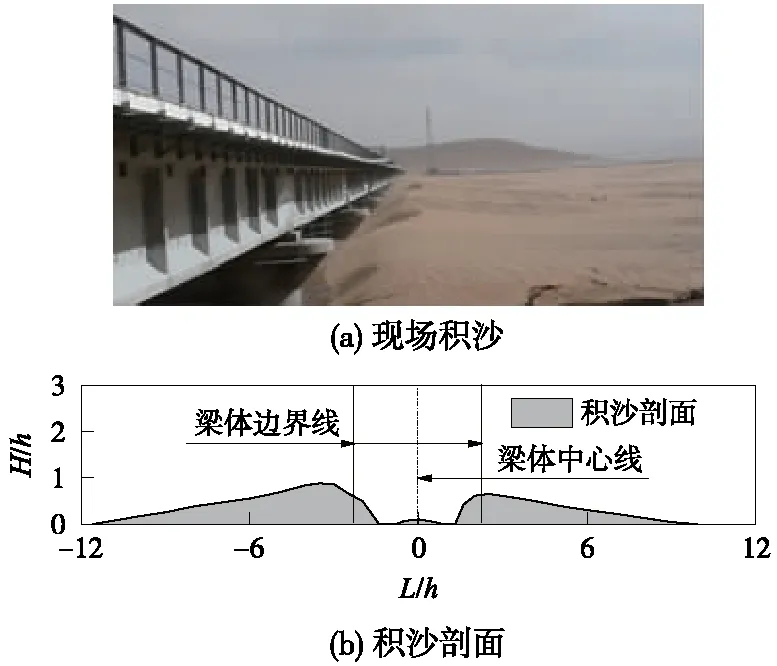
图6 某低净空桥梁现场积沙以及其剖面

3.3 T梁周围积沙演化规律

图7为T梁周围沙相体积分布随时间的变化规律，不难发现，当t=200 s时，梁体迎风侧、背风侧及正下方的风积沙堆相互独立，随着时间的推移，上述3个位置的积沙量及积沙范围均呈递增趋势，但它们之间的净距呈递减趋势，当t=4 000 s时，积沙量和积沙范围进一步扩展，使得上述3个沙堆有连成整体的趋势。需要注意的是，梁体周围的初始积沙主要是由于流场结构引起的，但逐渐增加的沙堆体积会反过来再次影响流场结构，从而加速沙堆体积增加的速率，如此反复形成恶性循环，最终堵塞桥梁，进一步影响桥上列车的安全运行。

图7 T梁梁体周围沙相体积分布随时间的变化规律(纵横比例尺为2∶1)

3.4 T梁净空对积沙的影响

图8为t=4 000 s时不同净空条件下T梁周围沙相分布，很容易看出，梁体周围的积沙量对梁底净空十分敏感，并随着净空增大呈递减趋势，当净空达到5.0 m时，梁体背风侧和正下方的沙堆消失，仅在迎风侧出现一处沙堆，且沙堆体积也非常小。主要原因有两点：①随着梁底净空增大，梁体对风沙流的扰动能力变差，大部分沙粒可以顺利通过，故积沙量呈递减趋势；②风沙流中沙粒含量随着高度呈递减趋势，因此腹板间绕流作用引起的积沙量也呈递减趋势。综上所述，为减小或者消除梁体周围产生的积沙，建议风沙地区的梁底净空不宜小于5.0 m。

图8 不同净空条件下箱梁和T梁底部积沙形态(纵横比例尺为2∶1)

3.5 梁体类型对流场及积沙的影响

图9为箱梁和T梁底部不同高度处相对风速对比。很明显，在梁体正下方同一高度处箱梁相对风速明显大于T梁，这说明箱梁底部气流的加速效应更加明显，高速气流使得箱梁底部积沙概率更低。此外，注意到在梁体背风侧附近(L=2.5h～7.5h)，箱梁的相对风速略微大于T梁，这可能导致前者在该区域的积沙概率更高。

注：XL代表箱梁，TL代表T梁。图9 箱梁和T梁底部不同高度处相对风速对比

图10为t=4 000 s箱梁和T梁底部积沙形态对比，可以看出箱梁底部的积沙量远小于T梁。此外，还可以观察到，T梁正下方存在积沙现象，而箱梁正下方无积沙，这主要与梁体几何形状有关：箱梁底部是平面，不存在类似于T梁的绕流现象，一般不会在梁底产生积沙。上述分析表明，同等条件下箱梁周围的积沙速率更低，在工程条件允许时，风沙灾害严重的地区低净空桥梁宜优先使用箱梁。

图10 t=4 000 s箱梁和T梁底部积沙形态对比(纵横比例尺为2∶1)

4 结论

基于计算流体力学软件，构建欧拉双流体非稳态数值模型，对梁体周围风沙流的运动特征进行深入剖析，并通过现场监测数据验证了数值模型的可靠性，主要得到以下结论。

(1)T梁周围的流场结构表明，梁体在其迎风侧和背风侧附近由于风速的衰减形成风积区，而在梁底的正下方由于风速加强形成风蚀区。

(2)T梁周围积沙主要分布在桥梁迎风侧、背风侧，而梁底正下方也存在少许积沙，且随着时间的推移积沙量均呈递增趋势，前者积沙主要与气流速度的衰减有关，而后者积沙主要与气流的绕流有关。

(3)随着T梁底部净空增大，梁体周围的积沙量呈递减趋势，当净空达到5.0 m时，仅在迎风侧出现一处体积很小的沙堆。为减小或消除梁体周围产生积沙，建议风沙地区的梁底净空不宜小于5.0 m。

(4)与T梁相比，箱梁底部气流的加速效应更加明显，相应的积沙速率也相对较小，故在工程条件允许时，风沙危害严重地区的低净空桥梁宜优先采用箱梁。