基于CFD-DEM的非球形颗粒水力输送数值模拟

陈 伟，张 佩，孙永昌，武煜坤，郑诚林，徐止恒，李政权

(江西理工大学 江西省颗粒系统仿真与模拟重点实验室，江西 赣州 341000)

由于结构简单、环保洁净、经济效益高等特点，管道水力输送已经成为目前最主要的尾矿运输方式，但在设备运行过程中，物料会对管道壁面造成侵蚀磨损现象，导致管道破损和设备故障[1-4]。侵蚀造成的管道壁面破裂会产生环境污染及经济损失[5-6]，而管道水力输送过程中磨损腐蚀问题最严重的地方是管道的弯头处，弯头磨损研究也引起越来越多国内外学者的关注。

近年来，计算流体力学(computational fluid dynamics，CFD)与离散元方法(discrete element method，DEM)作为经济、高效的多相流体系分析工具[7-10]，为研究管道磨损问题提供新的思路。Darihaki等[11]研究了管道颗粒输送时二次撞击的影响，获得现实的侵蚀预测；Chen等[12-13]采用单向耦合模型，利用Grant等[14]的实验结果开发出随机回弹模型，模拟了弯管和堵塞三通中的腐蚀；Duarte等[15]利用气-固流动的四向耦合模型，研究装有涡流室弯管中的腐蚀，发现涡流室提供缓冲效果，并减小侵蚀性；Zahedi等[16]使用CFD模型评估颗粒尺寸、流体速度、管道直径和颗粒回弹对长半径90°弯管侵蚀模式的影响；为预测三通管连接处的侵蚀模式，Zhang等[17]进行CFD分析，并将模拟结果与实际三通管连接处的失效分析进行比较，研究三通管的冲蚀磨损分布和失效机理；Blanchard等[18]利用循环回路系统研究平均曲率半径、管径比、颗粒尺寸对管道腐蚀的影响，结果表明，在不同尺寸颗粒或弯管特性的条件下，弯管的最大侵蚀角位置几乎相同；Wood等[19]使用一个实验回路来探索直、弯曲导管的腐蚀速率，发现弯管外壁的侵蚀比较显著，弯管底部侵蚀最严重。

水力输送弯管磨损的现有研究中，基本都是采用球形颗粒模拟输送物料，没有考虑颗粒形状的影响，而在实际输送过程中，矿物颗粒以非球形为主，所以模拟结果与实际结果出现的误差偏大。本文中以弯管为研究对象，采用3种不同长径比的颗粒，对水力输送过程中弯头处产生磨损的机理、颗粒动力学特性进行研究。

1 理论介绍

采用CFD-DEM耦合方法[20-21]，液相作为连续相，在欧拉坐标系下求解纳维-斯托克斯方程；颗粒作为离散相，在拉格朗日坐标系下求解颗粒运动方程。

1.1 连续相控制方程

液相作为连续相满足连续方程和动量守恒方程。液相连续性方程为

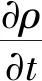
(1)

动量守恒方程为

(2)

标准k-ε模型中的湍动能k和湍动能耗散率ε，计算方程为

(3)

(4)

式中：k为湍流动能，J；ε为湍流动能耗散率；ui为平均速度，m/s；xj为空间坐标，m；μ1为层间流动黏性系数；μt为湍流黏性系数；Gk为由速度产生的湍流动能，m2/s2；Gb为浮力所产生的湍流动能，m2/s2；Ym为表示可压缩湍流中的波动膨胀对总耗散率的贡献，m2/s2；C1ε、C2ε、σk、σε为经验常数；Sk、Sε为源项。

1.2 离散相控制方程

颗粒相作为离散相遵守牛顿第二定律，将颗粒的运动分解为平动和转动，其运动方程分别为

(5)

(6)

式中：mp为颗粒质量，kg；up为平移速度，m/s，Ip为转动惯量，kg·m2；ωp为角速度，rad/s；Fw-p、Fp-p、Ff分别为壁面对颗粒的力、颗粒之间作用力、流体对颗粒的作用力，N；Mp为颗粒所受力矩，N·m。

1.3 连续相与离散相相互作用

连续相与离散相之间通过动量交换实现耦合，液固耦合作用力计算公式为

(7)

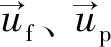
曳力模型计算公式为

(8)

式中：fd为流体对于颗粒的曳力，N；A为颗粒的投影面积，m2;CD为与颗粒雷诺数Re相关的阻力系数。

CD计算公式为

(9)

颗粒雷诺数定义计算公式为

(10)

式中：Re为颗粒雷诺数，dp为颗粒直径，m，μ为流体黏度，Pa·s。

1.4 磨损模型

本文中采用的磨损模型为Archard磨损模型，该模型中管道表面移除的材料量与在表面上移动的颗粒所做的摩擦功成正比。Archard磨损模型的基本方程为

Q=WFndt，

(11)

式中：Q为材料被移除的体积，m3；Fn为颗粒与壁面接触的法向力,N；dt为颗粒沿壁面的切向滑动距离,m；W为初始磨损常数。

磨损常数W的计算公式为

W=K/H，

(12)

式中：K为无量纲常数，取值与润滑条件、温度、摩擦系数等有关，一般需要实验获得，并且根据接触条件的不同在10-8～10-2之间波动，初定无量纲常数K为3×10-3；H为材料的最软表面布氏硬度，Pa；模拟的管道材料为铝，取H为1×107Pa，从而计算出磨损常数W为3×10-10Pa-1。

在离散相中每个单元的磨损深度公式为

Hp=Q/a，

(13)

式中：Hp为离散相中每个单元的磨损深度，m；a为颗粒与壁面的接触面积，m2。

2 模型的建立及边界条件

2.1 弯管模型建立

文中所研究的弯管道为Chen等[22]在2004年实验中所用的管道，弯管道的几何结构如图1(a)所示：管道包括1 200 mm的垂直输送部分、90°弯头部分、100 mm出口部分，管道直径D为25.4 mm，弯头处曲率半径R为1.5D。图1(b)为弯头示意图。

2.2 网格划分

采用Soildworks三维软件构建弯管道的三维模型，不考虑管道弯头处接口部分的影响。采用ICEM软件对弯管道进行网格划分，使用六面体结构化网格，计算更精确，速度更快。对管道划分网格时，为了在满足计算精度的同时尽可能减少网格数量，在弯管垂直段使用了粗网格，在弯头段和弯管出口段对网格进行了加密处理[23]。弯管道网格如图2所示，弯管道截面处网格如图3所示。

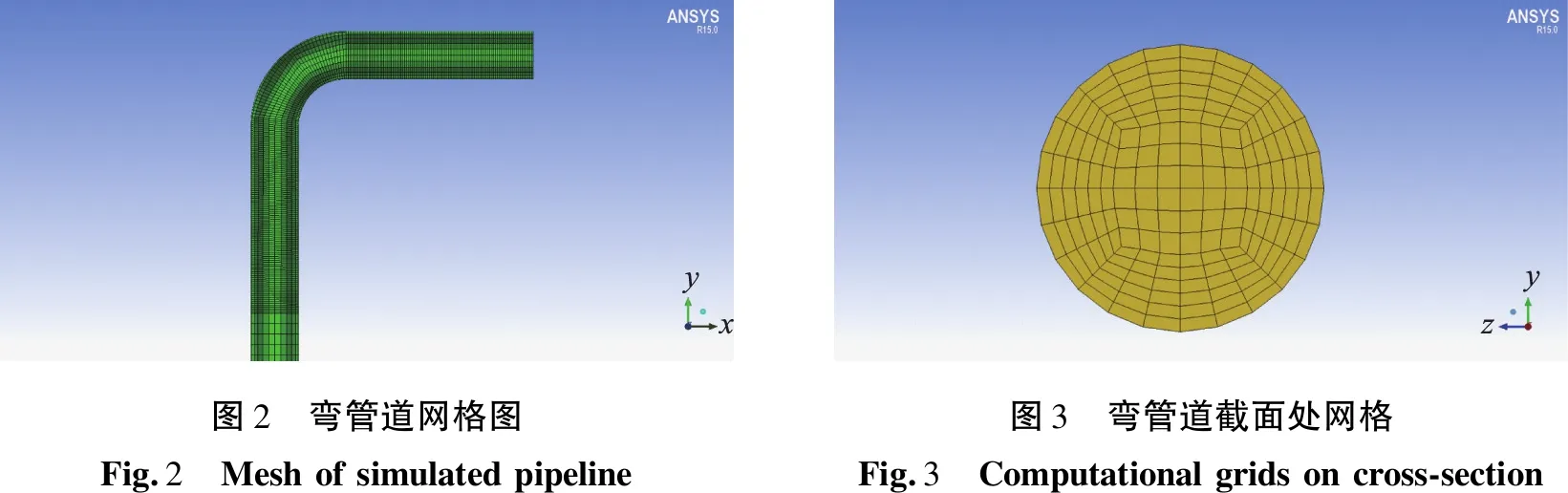
图2 弯管道网格图Fig.2 Meshofsimulatedpipeline图3 弯管道截面处网格Fig.3 Computationalgridsoncross-section

2.3 物性参数、边界条件

由于管道输送的颗粒数庞大，会对流体产生显著影响，因此采用双向耦合的方法，并充分考虑颗粒固体体积分数对流动状态的影响。

在耦合仿真中，管道入口设置为速度入口，流体输入速度为4.1 m/s，颗粒的输入速度为流体的2/3，管道出口设置为压力出口。管道壁面设置为无滑移边界条件，颗粒的输入流率为0.208 g/s。文中使用了3种颗粒，单球颗粒粒径为150 μm，双球颗粒由2个中心距为75 μm的单球颗粒组成，三球颗粒为相邻中心距75 μm的3个单球颗粒组成，颗粒模型如图4所示。具体固相物性参数见表1。

表1 固相物性参数Tab.1 Solid phase physical parameters

3 结果与讨论

3.1 实验验证与网格无关性验证

因为已知水力输送相关文献中未找到合适的弯管处相关磨损数据，所以此处采用了弯管气力输送的实验数据来验证模型正确性[22-23]。模型验证采用双向耦合的方式进行计算，模拟条件与实验条件完全一致，并且采用与实验相同的方式提取弯头外侧中心线的磨损数据，模拟与实验结果对比见图5。由图可以看出，模拟结果中随着角度的增加，磨损率呈先增大后减小的趋势，在45°左右达到了峰值。模拟结果可以较准确地预测磨损位置、磨损率的变化，初步验证了文中采用计算模型、模拟方法的正确性。

图5 模拟与实验结果对比Fig.5 Comparison of simulation and experimental results

3种颗粒在相同的条件下进行模拟计算，液相性质见表2。

表2 液相性质Tab.2 Liquid phase properties

由于计算量过大，因此需要对网格数量进行约束。使用3种数量的网格进行计算，分别是粗网格(66 768个)、中网格(84 148个)和细网格(113 360个)。图6所示为3种网格模拟结果与实验对比。由图可知，3种网格都可以预测磨损率变化趋势。中网格和细网格可以更准确地预测弯头处的磨损位置与磨损大小，粗网格有一定误差。

图7所示为3种网格最大磨损率对比。中网格的最大磨损率与细网格的最大磨损率没有太大变化，粗网格的最大磨损率相对较低。综合考虑计算资源与计算时间，采用中网格进行计算。

3.2 弯管道磨损位置分析

图8所示为弯头外侧中心线取值点示意图，文中角度值均依此取值。图9所示为输送单球、双球、三球颗粒5 s时的磨损云图，磨损较严重区域集中在弯头出口处，大致为弯头外拱中心线70°～90°处；同时，流率相同的情况下，颗粒的长径比越大，磨损越严重，磨损面积越大，与Bilal等[24]在2021年的实验结果类似。

图8 弯头外侧中心线取值点Fig.8 Value point of center line outside elbow

图9 输送单球、双球、三球颗粒5 s时的磨损云图Fig.9 Wear cloud diagram of single ball,double ball and three ball particle conveying at 5 s

通过颗粒运动轨迹来研究磨损机理，结果如图10所示。为了使选取的颗粒更具代表性，文中选取颗粒时进行了如下处理：把入口处管道截面分成9份，每份中随机取1个颗粒进行颗粒轨迹分析。单球颗粒的运动轨迹相对平缓，与弯管外拱相交较少，原因主要是单球颗粒的质量更小，在弯头处更容易受到液体的影响，不触碰管道壁面直接输送至出口。随着颗粒长径比增大，颗粒运动轨迹线与弯管外拱相交逐渐增多，三球颗粒相交最多，间接反映了三球颗粒输送时管道磨损量最大的原因。同时，当颗粒的长径比变大时，在弯头内拱处的空白区域逐渐变小，这是颗粒在流体与弯头共同影响下的结果，将在管道流态分析中讨论。

3.3 弯头处的磨损率

当颗粒形状变化时，单球、双球、三球颗粒输送稳定后磨损率对比结果如图11所示。3种输送情况在弯头处的磨损率都随中心线角度增大而增大，在70°～90°区间磨损率增大趋势更加明显，在90°处达到最大值。磨损率随着颗粒长径比的增大而增大，三球颗粒输送时的磨损率最大。这是因为当颗粒的长径比增大时，流体对颗粒的曳力也随之变大，所以三球颗粒更容易聚集在弯头出口处的上方，与弯管外拱壁面碰撞概率增大，致使出现更大的磨损区域，磨损也最严重。三球颗粒在弯头90°处的最大磨损率约是单球颗粒的2.4倍。

图11 单球、双球、三球颗粒输送稳定后磨损率对比Fig.11 Comparison of wear rate of single ball,double ball and three ball particles after stable transportation

3.4 输送流态对比

通过颗粒流态的分析来研究管道磨损的内在机理。图12所示为单球、双球、三球颗粒输送稳定后输送流态，由于颗粒的尺寸过小，因此管道中的颗粒放大了4倍显示。

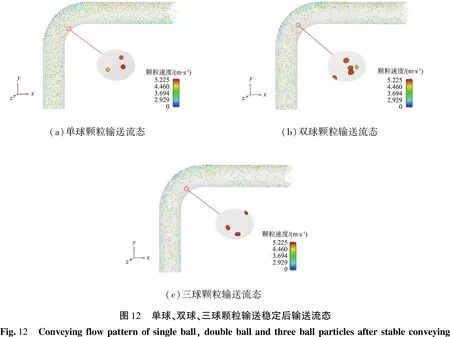
由流态图可以看出，在弯头内拱处颗粒较少，颗粒主要集中在弯头外拱区域。这是因为颗粒在弯头外拱区域聚集后，碰撞概率增大，在弯头外壁处碰撞后在惯性作用下向下方运动。同时，颗粒长径比越大，弯管外拱区域颗粒越密集，所以三球颗粒输送时的磨损最严重。在相同条件下，颗粒长径比越大，弯管内拱区域颗粒密度越低，说明在工业生产中弯头的内拱处可以适当减弱防护，增加经济效益。

3.5 颗粒浓度对比

单球、双球、三球颗粒输送在5 s时固体浓度分布见图13。相对于单球颗粒，双球颗粒和三球颗粒弯头处固体体积浓度明显增大，三球颗粒时最大，表明随着颗粒长径比的越大，颗粒在弯头处的集聚现象越来越显著，而颗粒集聚直接导致颗粒与弯管内壁的碰撞加剧，磨损愈加显著。颗粒集聚主要集中在弯管出口段的顶部，这是弯管顶部壁面磨损最严重的内在原因。

3种输送截面处的固体体积分数如图13(d)所示。在刚进入弯头时，即截面1位置时，3种输送管道内都呈现分散趋势；在弯头出口即截面2处，颗粒大部分聚集在管道的上部，还有少部分颗粒分散在管道的中上部分，这是颗粒在弯头外拱区域聚集所致。在出口中部即截面3处，颗粒相较于截面2处更加集中在管道上部，少部分颗粒因颗粒的重力和弯头的阻挡而聚集在管道底部，颗粒长径比越小，此现象越明显；当颗粒离开管道即截面4处，颗粒主要聚集在管道外壁处，且长径比越小的颗粒在外壁处分散越均匀。总的来说，在管道内三球颗粒分布最集中，对管道的磨损最严重。

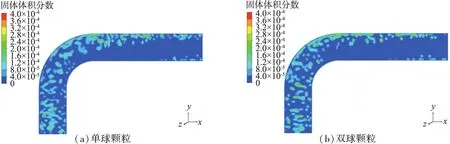
(c)三球颗粒

4 结论

1)磨损较严重区域集中在弯头出口处，大致为弯头外拱中心线70°～90°处；流率相同的情况下，颗粒的长径比越大，管道磨损越严重，磨损面积越大。

2)随着颗粒长径比增大，颗粒运动轨迹线与弯管外拱相交逐渐增多；管道流态中弯管外拱区域颗粒密集度逐渐增大，固体体积分数逐渐增加，表明颗粒与管壁碰撞加剧，间接反映了三球颗粒输送时管道磨损量最大的原因。

3)弯头处的磨损率随中心角角度增大而增大，在90°处达到最大值，三球颗粒在弯头90°处的最大磨损率约是单球颗粒的2.4倍。