基于结构协同的PM2.5粒子切割器性能提升
邹亚雄,任晓庆,刘伟光,刘 巍,张泽武,闫 骏
(青岛市计量技术研究院 环境监测仪器产业计量与测试中心,山东 青岛 266000)
随着大气污染问题的日益严峻,空气质量监测和预报已成为治理空气污染、保障民众健康的重要手段之一[1-5]。PM2.5粒子切割器是一种将颗粒按照粒径进行分离并实现50%切割粒径为2.5 μm的装置,进而用于对大气中的细颗粒物浓度进行测量[6-8]。学者在切割器的原理与设计方法上,进行了大量的理论和实验研究[5,9-19]。Kenny等[20]在Smith等[21]提出的5级旋风结构的基础上进行改进,设计出了VSCC(very sharp cyclone cut)型PM2.5粒子切割器,并于2006年被美国环境保护局(EPA)采纳为参考切割器。作为一款经典切割器,由于其测试精度高,形式简单,VSCC型结构参数被国内外众多厂商沿用至今,相关尺寸未进行过明显改动。

切割器性能稳定是空气质量监测准确度的保障,而切割数据的拟合方法则影响了切割性能评价的合理性。目前国内外学者在切割器实验数据的回归上所采用的方法各有不同,如二次函数、Sigmoid函数等[23-26],而通过不同拟合曲线反演出的切割性能指标也各有不同,会影响到对切割器性能优劣的判断,因此针对实验数据的拟合方法有待进一步研究。
综上分析可见,为了实现对切割器的切割性能进行准确评价,诸多学者针对测试方法和评价方法开展了大量的研究工作,然而却未能就影响评价的重要因素之一——切割曲线的拟合方法达成统一意见。在切割器性能的不断升级过程中,自VSCC型PM2.5切割器问世之后,在结构尺寸方面便鲜有改进,切割性能长期止步不前。为了进一步挖掘旋风式PM2.5切割器的性能提升空间,本文中通过优化切割曲线的σg来提高切割器长期运行过程中50%切割粒径的稳定性,以提高空气颗粒物浓度测试的准确性,延长设备维护的周期。
1 实验
1.1 主要仪器设备
LAP 322粒径谱仪(德国托帕斯高聚合物股份有限公司);M Series流量控制器(美国艾里卡特科技有限公司);VSCC型PM2.5旋风式切割器(国内某厂商)。
1.2 原理与方法
常用的粒子切割器包括撞击式和旋风式,其分离原理见图1所示。撞击式切割器主要由射流喷嘴与撞击板构成,当气流经过喷嘴加速后,气流中粒子具备了一定的动能,当气流冲击撞击板时,惯性较大的颗粒从气流中逃离出被撞击板截留,而惯性较小的颗粒将继续跟随气流进入下游。旋风式切割器主要由进、出口及柱锥段构成,当气流从进口切向冲击到柱段内表面后,受柱锥段结构影响作螺旋运动。在离心力作用下,具有较大惯性的颗粒从气流中脱离,贴附在切割器内表面或下滑至沉砂池中,反之则随气流从切割器下游排出。在工作过程中,由于部分颗粒截留在切割器内部,因此当积累量达到一定程度时其50%切割粒径会偏离设计点,造成测量数据失真,此时需将切割器拆开进行清洁、维护,以便下次使用。

参照HJ 93—2013[22]中对切割器性能的测试规定,可采用分流法或静态箱法。本研究中以自行搭建的分流法测试装置为例,采用如图2所示的测试流程,对PM2.5切割器切割性能进行测量。测试环节包括空压机供气、气溶胶发生、过渡段整流、干燥段除湿,之后气流携带颗粒从上游流路或下游流路流入粒径谱仪和流量控制器。上游流路用于测量进入切割器的颗粒数浓度,下游流路用于测量经过切割器切割作用后的颗粒数浓度,粒径谱仪用于对上、下游颗粒的数量进行计数。该装置所用的粒径谱仪流量为3 L/min,流量控制器流量为13.7 L/min,切割器工作流量为16.7 L/min。

图2 基于分流法的PM2.5切割器切割性能测试流程Fig.2 Testing process of PM2.5 cutter penetration performance based on divided flow method
为评价切割器对不同粒径颗粒物的切割效率,测试过程中分别采用规格为GBW13642—GBW13649、粒径分别为1.5、2.0、2.2、2.5、2.8、3.0、3.5、4.0 μm的单分散固态球形气溶胶颗粒通过PM2.5切割器,不同粒径的实验组间以纯净水彻底吹洗系统管路,以保证管路内残留的颗粒数量不影响对下一粒径数量浓度的测量。某一粒径颗粒物的切割效率表示为:
(1)
式中:ηi为粒径是i的粒子的切割效率;Ni为流出切割器下游每单位体积内的颗粒个数,cm-3;Mi为流入切割器上游每单位体积内的颗粒个数,cm-3。
2 拟合函数对切割性能的影响
由于切割器性能是由拟合后的切割曲线反演得到,因此采用不同拟合方程得到的切割性能存在差别,进而影响到对切割性能的评价。目前诸多学者采用S型曲线进行切割效率拟合,典型的S函数有Logistic形式和Gompertz形式[27],考虑其反对称函数形式与穿透率曲线形状类似,可尝试作为拟合的函数形式。此外也采用形式更为复杂的Sigmoid-8092函数对穿透率进行拟合[22],式(2)—(4)为3种拟合函数的方程。
Logistic函数:
(2)
Gompertz函数:
y=abcx,
(3)
Sigmoid-8092函数:
(4)
式中:a、b、c、d、e为拟合常数;x为自变量,表示实验颗粒物的空气动力学直径,μm;y为因变量,表示颗粒物的切割效率,%;exp为以自然常数e为底的指数形式。
利用Origin中的非线性拟合功能,采用以上3种函数分别对4组切割性能实验数据进行拟合,结果如图3所示。由图可见,通过3种函数拟合得到的切割曲线均与个别实验值间存在一定偏离,但拟合曲线能够表达出切割效率随粒径增大而递减的趋势,没有出现严重的拟合失真现象。这3种函数拟合方式之间也存在差别,Logistic与Sigmoid-8092在起点和终点位置均穿过实验值,Gompertz函数在对4个样本进行拟合时,均未能在起始处穿过实验值,而在其他实验点上Gompertz拟合曲线的偏离度也要比其他2种更为明显,因此Logistic与Sigmoid-8092在拟合切割曲线时效果更好。

(a)Logistic函数拟合
为便于进一步对比这3种非线性函数拟合的精度,采用实验值与预测值之间的线性回归进行分析[28],理想状态判别条件如下:
1)实验值与预测值之间的线性回归关系为Y=X。
2)拟合值同实验值之间线性回归的拟合度R2=1。
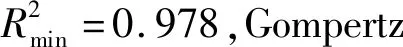

3 切割器结构尺寸对切割性能的影响
3.1 VSCC型切割器性能
在对切割器的性能进行优化之前,有必要了解目前VSCC型切割器的性能情况。通过分流法测试5个不同批次的VSCC型PM2.5旋风式切割器,采用Sigmoid-8092函数进行拟合,拟合软件为Origin,通过拟合曲线反演出切割器的性能指标数据,见表1所示。

表1 不同批次VSCC型切割器的切割性能Tab.1 Performance data of VSCC cutters from different batches
在对表1数据进行分析前,首先了解切割器的理想切割曲线形式,如图5所示。对于理想切割曲线而言,粒径大于Da50的粒子均被分离出来,而粒径小于Da50的粒子均随气流从切割器出口流出。由于理想切割曲线的Da84=Da50=Da16,即σg=S=1,因此实际切割曲线的几何标准偏差σg和锐度S越接近1,其对颗粒的分离精度就越高,同时也越利于在长期使用过程中维持50%切割粒径的稳定性。

图5 理想切割曲线与实际切割曲线Fig.5 Ideal and actual penetration curve
分析表1中数据可以看出,VSCC型切割器的50%切割粒径Da50分布在2.32~2.52 μm,几何标准偏差σg分布在1.15~1.30,切割曲线锐度S在1.20~1.24,本文中的实验数据与文献[25]的测试数据基本吻合,并满足参考切割器的性能指标要求。为了更进一步提升切割器的性能,在现有的基础上可将Da50由规定的±0.20 μm偏差范围减小到±0.10 μm以内,σg的分布在1.15~1.30基础上下调最大值,从而使其分布区间减小,切割精度提高。
初步分析不同结构位置及结构尺寸对切割性能的影响规律。以VSCC型切割器为例,其主要结构尺寸包括进口直径Din,出口直径De,圆柱段直径Ds和高度Hs,圆锥段高度Hc和锥底直径B,见图6所示。由Kenny等[29]的研究表明,进口与锥段结构尺寸对切割性能的影响要远大于出口,而底部沉砂池的影响基本可以忽略,说明进口、锥段是优化的重点部位。最后考虑到工作风量Q、圆柱段直径Ds和Da50等三者之间可以用方程进行描述[30],其关系见式(5)所示,因此在Q和Da50均保持不变的情况下,Ds也应维持原值不变。

图6 PM2.5旋风式切割器的主要结构Fig.6 Primary structures of PM2.5 cyclone cutter
lnDa50=a+blnDs-(b-1)lnQ,
(5)
式中:Da50为50%切割粒径,μm;Ds为旋风型切割器圆柱段直径,cm;Q为切割器的工作风量,L/min;a、b分别为采用最小二乘法拟合出的经验系数。
综上分析,以进口直径Din、出口直径De、圆柱段高度Hs、圆锥段高度Hc和锥底直径B为结构优化对象,通过调整结构尺寸寻求切割性能的变化规律,从而在VSCC型PM2.5切割器的基础上减小σg,实现进一步提升切割器性能的目的。VSCC型切割器原结构参数尺寸见表2所示。

表2 VSCC型切割器原结构尺寸Tab.2 Original structure dimensions of VSCC cutter mm
3.2 进口直径Din的影响
根据前文分析对各结构尺寸的影响进行研究。调整进口直径Din,方案见表3所示,表4所示为切割性能实验数据。图7所示为切割曲线,其粒径点对应的切割性能是采用5次测试数据的平均值给出,并绘制了误差范围。由图可以看出,Da50、σg以及S随Din的减小而减小,说明可以通过缩小Din来减小σg和S,但Da50也会随之发生变化。以序号3结构为例,其σg和S较小,但Da50=2.16 μm与目标值2.5 μm偏离较大。可见单独调整Din大小无法满足减小σg而不改变Da50的要求。

表3 进口直径方案Tab.3 Schemes of inlet diameters mm

表4 进口直径对切割性能的影响Tab.4 Effect of inlet diameter on penetration performance

图7 不同进口直径对切割效率的影响Fig.7 Effects of different inlet diameters on penetration efficiency
3.3 出口直径De的影响
对出口直径De进行调整,方案见表5所示,表6所示为切割性能实验数据,图8所示为切割曲线对比。当De增大时,Da50增大而σg与S在减小,说明可以通过增大De来减小σg和S,但Da50也会变大。以序号3结构为例,尽管其σg和S较小,但存在Da50向大于2.5 μm方向偏离的趋势,因此单独调整De大小也无法满足优化的要求。

表5 出口直径方案Tab.5 Schemes of outlet diameters mm

表6 出口直径对切割性能的影响Tab.6 Effect of outlet diameter on penetration performance

图8 不同出口直径对切割效率的影响Fig.8 Effects of different outlet diameters on penetration efficiency
3.4 圆柱段高度Hs的影响
对圆柱段高度Hs进行调整,方案见表7所示,表8所示为切割性能实验数据,图9所示为切割曲线对比。可以看到,随着Hs增大,Da50变大,σg与S在小幅增大后趋于稳定。为了减小σg与S的大小,需要降低圆柱段的高度,但从表8中可知Da50会向更小的方向偏离2.5 μm。考虑σg与S随Hs的变化速率缓慢,所以必须对Hs进行较大尺寸调整才能改变σg,这样不仅会减小Da50,而且使得入口同颗粒分离段的过渡空间大大减小,使进口来流影响到柱锥段对颗粒的分离过程,因此在优化切割器性能的过程中,现有的圆柱段高度Hs不适宜进行调整。

表7 圆柱段高度方案Tab.7 Schemes of cylinder heights mm

图9 不同圆柱段高度对切割效率的影响Fig.9 Effects of different cylinder heights on penetration efficiency

表8 圆柱段高度对切割性能的影响Tab.8 Effect of cylinder height on penetration performance

表9 圆锥段高度方案Tab.9 Schemes of cone heights
3.5 圆锥段高度Hc的影响
对圆锥段高度Hc进行调整,方案见表9所示,表10所示为切割性能实验数据,图10为切割曲线对比。可以看到,Da50随Hc的增大缓慢增加,而σg的前段与后段变化趋势相反,表现为Hc增大时σg前段增大而后段减小,从而令S基本保持不变。当调整Hc时,由于前后段σg朝着不同的方向变化,总体上使S几乎不发生改变,也就无法满足降低切割曲线σg这一优化目标,因此Hc同样不适宜进行调整。

表10 圆锥段高度对切割性能的影响Tab.10 Effect of cone height on penetration performance

图10 不同锥段高度对切割效率的影响Fig.10 Effects of different cone heights on penetration efficiency
3.6 锥底直径B的影响
对圆锥底部直径B进行调整,方案见表11所示,表12所示为切割性能实验数据,图11为切割曲线对比。可以看到,Da50随B的增大迅速增加,σg前段和后段也出现了类似Hc影响时的效果,即变化方向相反,同时切割曲线锐度S基本不变。与上述结构影响不同的是,锥底直径B对Da50的作用效果相比σg而言更加明显,说明适当调整B尺寸可以在改变Da50的同时不显著影响σg,因此可尝试与其他结构部位协同对切割性能施以改进。

表11 锥底直径方案Tab.11 Schemes of cone bottom diameters mm

表12 锥底直径对切割性能的影响Tab.12 Effect of cone bottom diameter on penetration performance

图11 不同锥底直径对切割效率的影响Fig.11 Effects of different cone bottom diameters on penetration efficiency
综上所述,排除不适宜调整的结构Hs和Hc,对Din、De和B进行进一步的分析。首先考虑De,表5中序号为2和3的不同De值所表现的切割性能相差不大,而序号2切割器的De值与VSCC原型切割器相等,可见De尺寸对切割性能的影响效果存在阈值。考虑惯性式切割器的切割曲线锐度与回旋段雷诺数Reann(根据文献[29],回旋段雷诺数使用下标ann表示)相关[31-33],即Reann越大则切割曲线的锐度越小,曲线的形状越陡峭。
旋风型切割器回旋段雷诺数Reann计算方法如公式(6)所示[34],可以发现,De增大反而会造成Reann的减小,恰恰不利于切割曲线锐度的提高,而产生表6中“De增大σg减小”的原因是由于Da50在右移的过程中对切割曲线挤压所造成的,即锐度的提升是以增大Da50为代价的,因此De值并不需要在原结构尺寸的基础上做进一步调整,因为这样存在使Da50增加的风险,不利于控制切割器的切割粒径值。其次,对于锥底直径B和进口直径Din来说,由于仅改动Din尺寸时Da50和σg同步缩小,不能实现单独优化σg的目的,考虑锥底直径B值可以在不对切割曲线锐度产生较大影响的基础上进而调整Da50,因此二者将作为协同优化切割器性能的主要结构进行研究。
(6)
式中:Reann为旋风式切割器的回旋段雷诺数;Vin为切割器进口风速,m/s;Rs为旋风切割器圆柱段半径,m;Rout为旋风切割器出口半径,m;υg为空气运动学黏度,20 ℃时为15.7×10-6m2/s。
4 结构间的协同优化
4.1 等同雷诺数法确定进口直径Din
由于Din和B对切割器性能的影响相互耦合,且切割性能受Din的变化影响较B更敏感,因此首先对进口直径的尺寸进行定量。表13所示为采用寻优进口结构的尺寸参数,分别测试其在工作风量为16.7 L/min、增大风量为17.5、18.5 L/min下的切割器性能,借以观察不同风量影响下的变化规律,测试数据见表14所示。第1行是VSCC原型切割器的性能同比数据,用于与其他方案(Din=7.60 mm)进行比对。可以看到,对于Din=7.60 mm方案,在18.5 L/min流量下的切割曲线性能较为符合2.40 μm≤Da50≤2.60 μm和1.15≤σg≤1.25的优化目标。

表13 Din尺寸优化方案Tab.13 Scheme of optimized Din dimension mm

表14 风量对切割性能的影响Tab.14 Effect of air quantity on penetration performance
由于切割器的常用工作风量为16.7 L/min,为了将该流量下切割器的Reann提高到与18.5 L/min流量时的一致,根据公式(6),在不改变Ds和De的前提下,可借助缩小Din来提高进口风速Vin进而增大Reann,将这种增加切割器进口风速进而实现不同风量下Reann等效的方法称作等同雷诺数法。经过换算后得到的工作流量16.7 L/min下的Din=7.22 mm,即改进后的切割器通过缩小Din尺寸使回旋段雷诺数Reann增大至4 633,该值较原VSCC型切割器的Reann=3 654高出了26.8%。
4.2 确定锥底直径B
在Din=7.22 mm的结构基础上对锥底直径B值进行优化,结构尺寸和测试数据见表15、16所示,实验风量为16.7 L/min,图12所示为切割曲线对比。首先可以看到,表14和表16所对应的2次测试中VSCC原型的性能较为接近,说明2次实验具有同比性。其次在Din缩小的情况下,小范围调整B值对切割曲线的锐度影响并不大,此外表16中序号为3的结构也表现出了Da50增大时σg后半段减小的趋势,这与前文研究De的影响规律吻合。除此之外,从序号为1和2的2种结构所对应的切割性能可见,优化后的切割器其Da50分布在2.50~2.60 μm,在保持Da50与2.50 μm偏离度不超过±0.10 μm基础上,切割曲线的几何标准偏差σg的最高点由1.30减小到了1.22。

表15 B尺寸优化方案Tab.15 Schemes of optimized B dimensions mm

表16 锥底直径B对切割性能的影响Tab.16 Effect of cone bottom diameter B on penetration performance

图12 不同锥底直径对切割效率的影响Fig.12 Effects of different cone bottom diameterson penetration efficiency
选定表15中编号1的结构作为优化切割器,分5次测试其切割性能,并根据实验数据拟合切割曲线,反演得到相应的切割性能数据见表17所示。可见改进的VSCC型切割器的Da50分布在2.52~2.57 μm,σg分布在1.15~1.24,S分布在1.18~1.21。

表17 改进型切割器的性能数据Tab.17 Performance data of improved cutter
为了更进一步对比改进型切割器性能提升的大小,根据文献[6]中的实验数据绘制了具有代表性的PM2.5粒子切割器以及VSCC型、改进型共5款切割器的切割曲线,对比如图13所示。由图可见,相比于UGR和GK2种旋风式切割器而言,WINS(well impactor ninety-six)、VSCC和改进型切割器的切割曲线在整个区间内均有较为明显的快速下降趋势,保障了切割器在长期使用过程中Da50的偏离度不至过大,进而影响到测量数据的准度。再之,本文中改进型切割器的Da50要比其余4种切割器偏大,但依然满足与2.50 μm偏离度不超过+0.10 μm的要求,且距离中心点粒径2.50 μm较VSCC型切割器更小。最后从文献[18]中可知,长期运行后因内壁颗粒数量的增多,切割器的Da50通常会减小。从表1中的实验数据可知,VSCC型切割器的Da50较集中在≤2.5 μm的范围内,因此随着使用时间的推移,Da50会不断变小直至偏离适用范围,而改进型切割器其Da50处于≥2.5 μm的范围内,随着内壁颗粒增多,Da50首先会从右侧靠近2.5 μm然后再偏离适用范围,这样就延长了切割器的有效工作时间。
从切割器的性能优化趋势来看,早先的GK和URG产品由于切割曲线相对平缓,使用时需要经常进行颗粒清理,不能很好地适用于高浓度、长时间采样工况,而后续设计的WINS和VSCC型切割器在面对上述工况时,对粒子均具备更佳的切割能力,因此被EPA采纳为参考切割器。由此可见,以减小切割曲线锐度进而提升切割性能的方式,是今后切割器技术升级的重要途径。

5 结论
1)采用结构间协同的方式对VSCC型PM2.5旋风式切割器性能进行改进,明确以进口直径Din和锥底直径B为优化对象、以Reann表征切割曲线锐度的思路,对相关结构尺寸进行定值,得到了满足切割器优化目标的结构形式。
2)将VSCC型PM2.5旋风式切割器的性能指标由Da50=2.32 ~2.52 μm、σg=1.15~1.30优化至Da50=2.52 ~2.57 μm、σg=1.15~1.25,减小了50%切割粒径和几何标准偏差的分布范围,使切割曲线向中心点值进一步靠近。
该方法为旋风型粒子切割器的结构设计和性能优化提供了思路。随着国内环境治理的不断发展,势必在今后对颗粒物采样仪器的测试精度有着更高的要求,不难发现目前切割器的σg距离理想值仍有一定差距,因此仍有大量工作有待进行。

