基于固定时间扩张状态观测器的底栖式AUV 点镇定控制
高鹏,万磊,徐钰斐,陈国防,张子洋
哈尔滨工程大学 船舶工程学院,黑龙江 哈尔滨 150001
0 引 言
海洋石油是地球上最丰富的自然资源之一,目前,其开发已从水深300 m 扩展至水深3 000 m的深海区,与之相应的海洋石油勘探也逐渐向深海发展。海底节点[1](ocean bottom node, OBN)地震数据采集技术是目前石油勘探最主要的手段之一。所谓OBN,即将地震检波传感器集群布放到海底,其可独立采集、记录海底数据。然而,大部分的OBN 产品无自主运动能力,主要通过水下遥控机器人(remote operated vehicle,ROV)逐个布放回收,其组网精度、回收效率均较低,难以满足地震勘测应用的大规模组网布放。
为解决这一问题,一种搭载地震检波装置的底栖式水下航行器概念被提出[2]。底栖式水下航行器将自主水下航行器(AUV)与地震检波技术进行了结合,是一种新型的海洋石油勘测设备。底栖式AUV 运动至海底目标位置后,可长期坐底采集海底地震数据,在作业完成后再上浮至指定海域,由母船统一打捞回收。
底栖式AUV 在坐底运动的过程中不可避免地会受到海底未知海流的干扰,而这将影响AUV的坐底位置,进而影响其海底勘探性能。因此,研究未知海洋环境下以及不确定性影响下的AUV点镇定控制及跟踪控制就显得尤为重要。
近年来,已有不少先进的控制方法被应用到了AUV 的运动控制系统中,包括反馈线性化控制、自适应控制、滑模控制[3-4]和反步控制等。其中,反步控制通过反向设计虚拟控制函数,可以使控制器的设计过程系统化、结构化,因而被广泛应用于多自由度系统的运动控制中[5]。然而,传统的反步控制方法存在2 个固有的弊端:其一是鲁棒性较差,常见的解决方案是将其与其他鲁棒控制方法相结合,例如自适应控制、滑模控制等[6];其二,即所谓“复杂性爆炸”问题,主要由虚拟控制的微分所引起,解决这一弊端的常用方法是加入非线性滤波器或是指令滤波器等[7]。
对AUV 控制系统而言,通常希望系统状态能在短时间内收敛。然而,传统的反步控制器是渐近稳定的,系统状态的平衡时间难以确定。终端滑模控制[8]是保证系统在有限时间内镇定的有效方法,即系统状态在有限的时间内收敛至平衡状态。然而,有限时间稳定系统的收敛时间依赖于初始状态,并有可能随着初始状态的增加而趋于无穷大。对底栖式AUV 而言,其点镇定控制的初始状态不可预测,故系统的收敛时间可能较长,这也直接影响了有限时间控制方法的应用。2015 年, Muralidharan 等[9]提出了固定时间稳定性,可以证明系统的收敛时间一致最终有界,且与初始状态无关。因此,可以通过反步法设计一种固定时间控制方案,以使控制系统在固定的时间内收敛。
此外,出于对自身重量以及节约成本方面的考虑,底栖式AUV 并未配备速度传感器,上述提及的基于完全状态反馈的控制方法很难保证优异的控制性能。而且,AUV 在水下运动时,经常会受到外部干扰以及不确定性因素的影响,若不考虑这些因素,控制系统有可能会不稳定甚至是发散。干扰观测器是解决上述问题的有效方法之一,其不需要知道系统模型的精确信息,仅通过已知状态量即可以实现对未知扰动或者其他未知状态的精确估计[10]。
基于以上分析,本文拟提出一种基于固定时间扩张状态观测器(fixed-time extended state observer,FTESO)的固定时间反步控制方案,以实现对底栖式AUV 在未知环境扰动以及不确定性因素影响下的点镇定控制。首先,设计一种固定时间扩张状态观测器,用于估计不可测量的速度以及集中扰动,且估计误差在固定时间内收敛;然后,基于该观测器,使用反步法设计固定时间反步AUV点镇定控制器,使AUV 的位姿误差可以在固定的时间内收敛至0;最后,引入非线性一阶滤波器,解决反步控制器固有的“复杂性爆炸”问题。
1 符号和预备知识
1.1 符 号
1)对于给定的向量, ||·||表示欧几里得L2 范数, |·|表示标量的绝对值。
2)对 于 给 定 向 量x=[x1,x2,···,xn]T,sigr(x)=[|x1|rsign(x1),|x2|rsign(x2),···,|xn|rsign(xn)],其 中r为任意实数, s ign(·)为符号函数,具体定义如下:
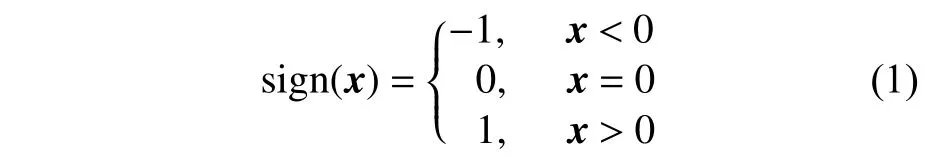
3) max(a,b)表示实数a与b之间的较大值,min(a,b)表示实数a与b之间的较小值。
1.2 预备知识
对于一类非线性系统x(t)[11],x=[x1,x2,···,xn]T,满足
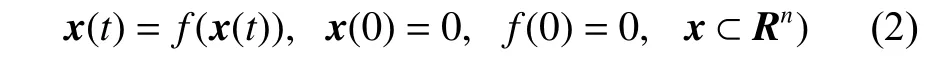
式中:f(·)为系统表达式;Rn为n维向量。
定义 1[10]:若存在一个函数V(x)满足以下3 个条件,则非线性系统的平衡点x= 0 是全局渐近稳定(globally asymptotic static, GAS)的,即
1)V(x)≤0,V(0)=0;
2)V(x)≥0(x≠0);
引理 1[12]:若非线性系统(式(2))满足
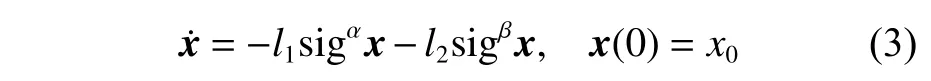
式中,α,β,l1,l2均为正常数,满足0 <α <1, β >1的条件,则非线性系统是固定时间收敛的,且收敛时间T满足
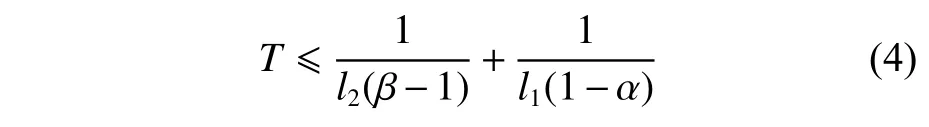
此外,若存在小的扰动 ζ,使非线性系统(式(2))满足
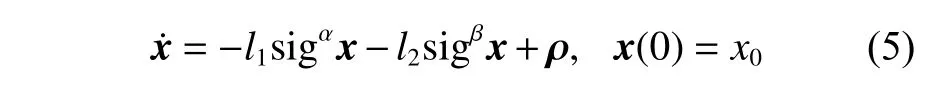
式中, ρ为一个小的正实数向量,则非线性系统是半全局固定时间一致最终有界(semi-global fixedtime uniform ultimate boundedness, SGFTUUB)[13]且可以在原点的邻域内收敛,且收敛时间T满足
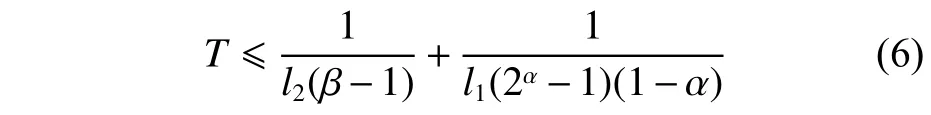
引理 2[14]:若存在正实数s,满足s≤sm+sn( 0 <m<1,n>1) ,则存在任意正实数k1,k2,k3>0,满足

引理 3[15]:若 存 在 正 实数 ξ1,ξ2,···,ξn≥0且指数h>0,则有
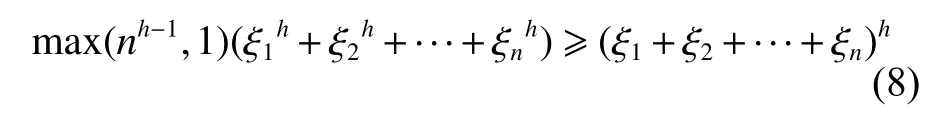
2 底栖式AUV 模型建立以及控制问题描述
2.1 底栖式AUV 模型建立
底栖式AUV 的模型如图1 所示,其中E-ξnζ和O-xyz分别为大地坐标系和随体坐标系。六自由度的AUV 运动学及动力学公式表述如下:

图1 底栖式AUV 示意图Fig. 1 Schematic diagram of benthic AUV
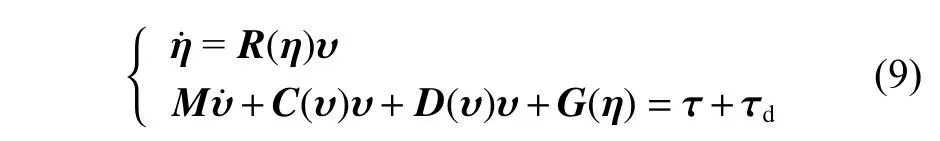
式中:η = [ξ,n, ζ,φ, θ, ψ]T,为AUV 的六自由度位姿信息,其中ξ,n,ζ 分别为AUV 的纵荡、横荡和垂荡,φ,θ,ψ 分别为横摇角、纵摇角和艏摇角;υ =[u,v,w,p,q,r]T,为AUV 的六自由度速度和角速度信息,其中u,v,w分别为AUV 的纵荡速度、横荡速度和垂荡速度,p,q,r分别为横摇角速度、纵摇角速度和艏摇角速度;R(η)∈R6×6,为从随体坐标系向大地坐标系的转换矩阵;M∈R6×6,为惯性矩阵;C(υ)∈R6×6,D(υ)∈R6×6,分别为科氏向心力矩阵和流体阻尼力矩矩阵,G(η)∈R6×1,为重力和浮力产生的恢复力(力矩)向量;τ ∈R6×1, τd∈R6×1,分别为AUV 的控制力(力矩)向量及外界干扰力(力矩)向量,其中控制力与力矩均由推进器作用产生。
底栖式AUV 装配了双主推、双垂推、双侧推共6 个推进器,通过推进器的共同作用来实现对6 个自由度的运动控制。因此,本文所描述的点镇定控制是在多推进器作用下的全驱动控制。
2.2 控制问题描述
假设1:
1) 目标的期望位姿 ηd有界且为二阶可导的。
2)C(υ),D(υ)为未建模的矩阵。
3) AUV 所受的未知环境力有界,即 ||τd||≤ε,其中 ε为一个很小的正常数。
4) AUV 的速度 υ不可测。
出于节约成本以及对自身重量的考虑,底栖式AUV 并未装载速度传感器,其目标位姿为常数,在海底附近运动时受到的未知干扰相对较小,因此,假设1 成立。
本文的控制目标如下:在满足上述假设的条件下,设计一种点镇定控制器,以使底栖式AUV的最终位姿 η能够在固定的时间T内镇定于期望位姿 ηd处。公式如下:

3 底栖式AUV 反步点镇定控制器设计
本节将设计一种FTESO 的固定时间反步点镇定控制器。首先,将式(9)所示的AUV 系统模型转换为适用于反步法的严格反馈形式。然后,设计一种弱抖振固定时间扩展状态观测器(weakchattering fixed-time extended state observer,WCFTESO),并基于观测值进行固定时间动态面反步控制器的设计。同时,引入一阶滤波器,以避免可能出现的“复杂性爆炸”问题。反步控制器的控制框架如图2 所示。
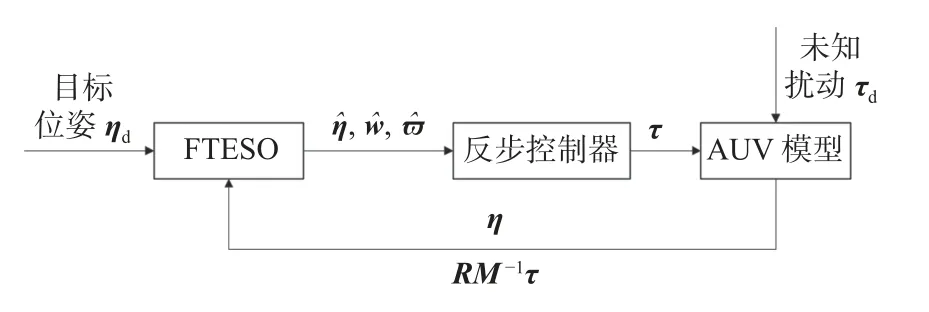
图2 反步控制器框图Fig. 2 Block diagram of backstepping controller
3.1 模型变换
为了更好地设计控制器,引入了新的变量w=R(η)υ并代入式(9),可以得到新的AUV 系统表达式:
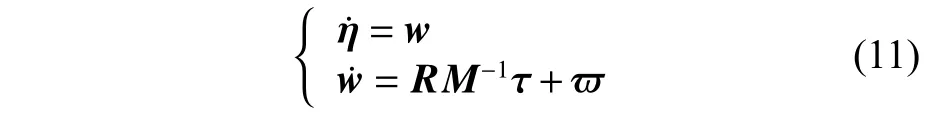
假设2:存在一个常数c, 使得 ||||≤c成立。
由于海底环境下的扰动明显小于近水面,且扰动的变化不大,因此,假设2 成立。
3.2 WCFTESO 观测器的设计
本文在文献[16]的基础上设计的WCFTESO 观测器只需输入AUV 的位姿信息即可实现对不可测量的速度以及未知集中扰动的观测。WCFTESO 的表达式如下:

与文献[17]不同的是,本文设计的WCFTESO使用了自适应项 ∂来代替传统的符号函数,避免了其值在正负之间来回振荡,从而可以有效解决观测误差的抖振问题。
证明:定义观测器的观测误差为

对式(13)进行求导,有
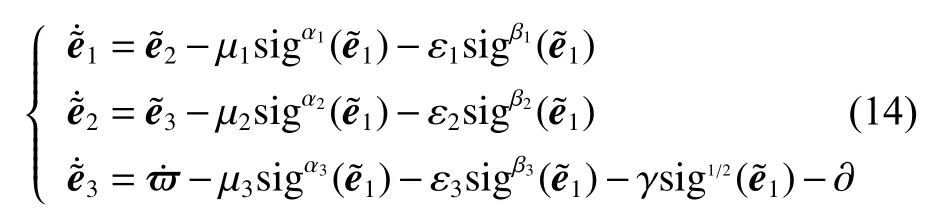
首先,证明下式的固定时间收敛性。
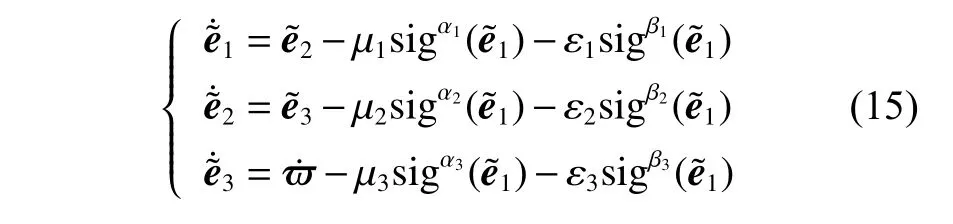
根据文献[17]中的定理2,可知式(15)可以在固定时间T1内收敛。


将观测值替代实际值并代入式(11),根据定理1,可以得出新的系统状态表达式如下:

3.3 基于WCFTESO 的固定时间动态面反步控制器设计
首先,定义2 个滑模面s1和s2。


根据引理1,可知e1,e2均在固定时间内收敛。因此,只需设计控制器,使滑模面一阶导为0 即可。
该方案的优点为:高架桥桥墩的桩基础直接作用于土层,高架桥沉降与车站沉降互不影响,工程可实施性较强,风险小。
然后,分别对上面2 个滑模面求导,并结合式(17),可得
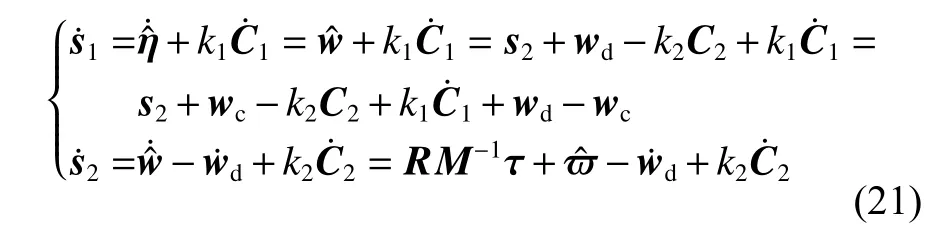
式中,wc为虚拟控制输入。
根据式(21),可设虚拟控制律如下:
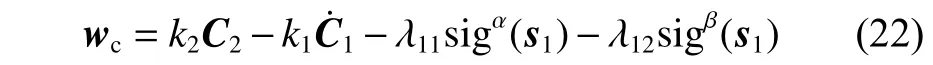
式中, λ11, λ12为正常数。
为了避免对虚拟变量直接微分引起的复杂计算量,引入了一个新的状态变量wd,wd表 示wc在时间常数 σ下通过一阶低通滤波器后的滤波值[18],其表达式如下:
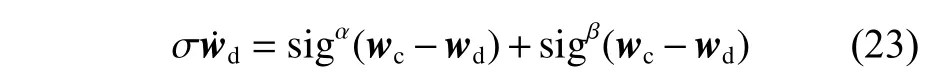
根据式(21)~式(23),设计系统的控制输入为
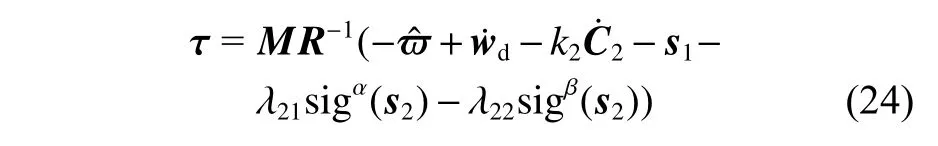
式中, λ21, λ22为正常数。
定理2:对于式(17),在满足假设1 和假设2的前提下,设计上述虚拟控制律及反步控制器,并结合非线性一阶低通滤波器以及WCFTESO 观测器,可以保证闭环系统是半全局固定时间一致最终有界的。
证明过程如下所示。选取李雅普诺夫函数V为
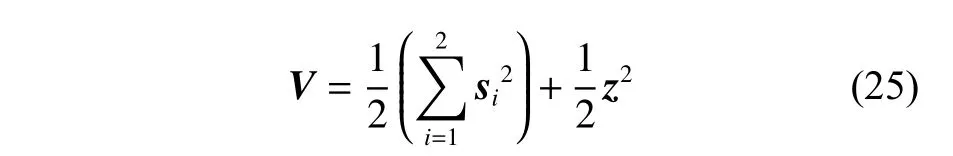
式中,z=wd-wc,为滤波误差。
z的一阶导可以表示如下:
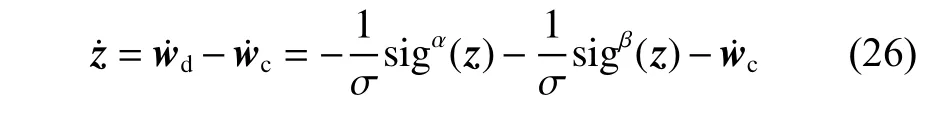
根据虚拟控制律(式(22))以及假设1,可知虚拟控制律wc的一阶导有界,即存在一个正常数向量δ,使其满足≤δ。
将式(25)关于时间t求导,并结合式(21)、式(24)和式(26),有
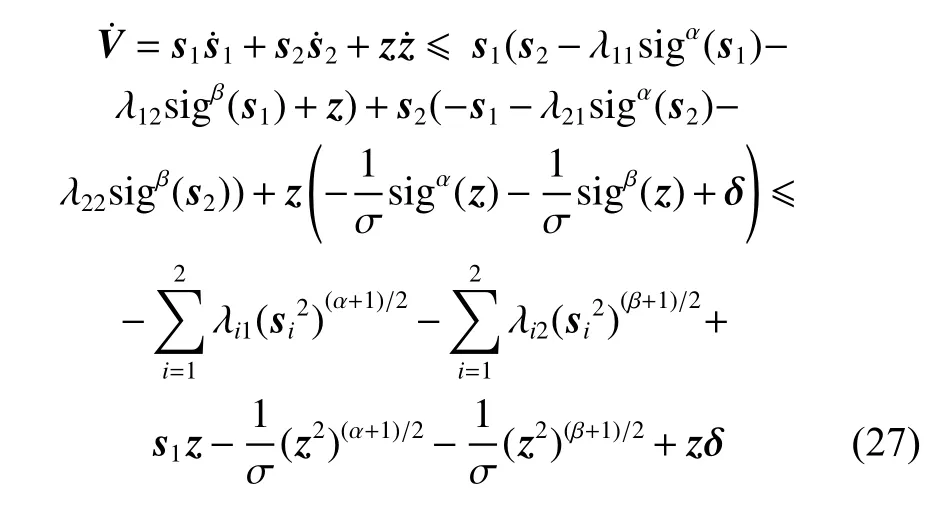
根据杨氏不等式 2xy≤x2+y2,式(27)可进一步转化为
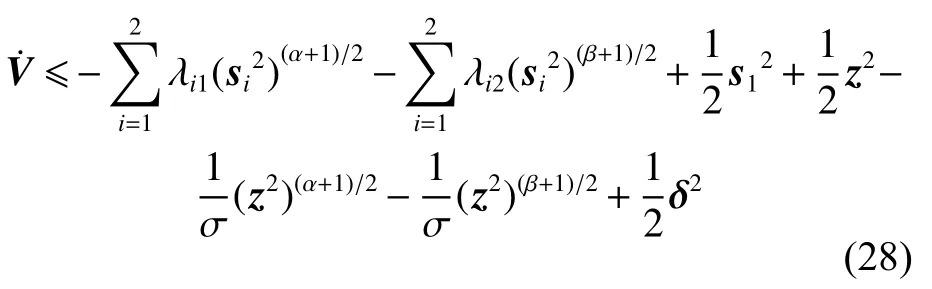
根据引理2,有
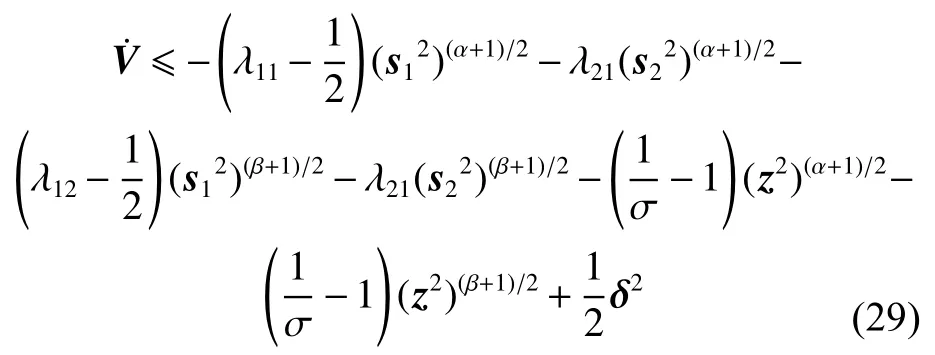
当控制器的参数符合 时,令
λ11,λ12>1/2,1/σ >1

将式(30)代入式(29),有
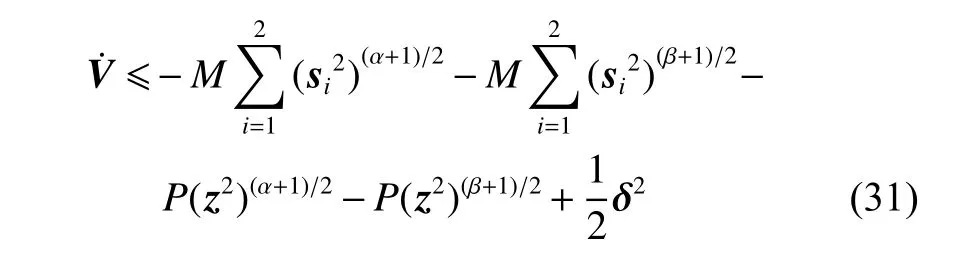
根据引理3,有
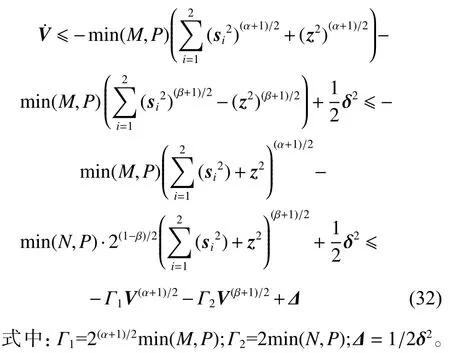
当选择合适的控制参数,并确保M,N,P皆为正时,根据引理1,可知式(25)是半全局固定时间一致最终有界的,且收敛时间TV满足

因此,可以证明在本文设计的控制策略下,式(17)可以在固定时间内收敛,且收敛时间T满足
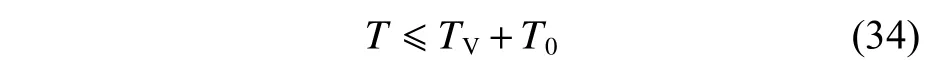
式中,T0为WCFTESO 的收敛时间。
4 仿真分析
本节将通过仿真分析,验证所设计点镇定控制器的跟踪效果,仿真选用的底栖式AUV 模型参数参见文献[19]。
仿真中, WCFTESO 的初始值为

WCFTESO 的参数以及本文所提控制器的参数选取为
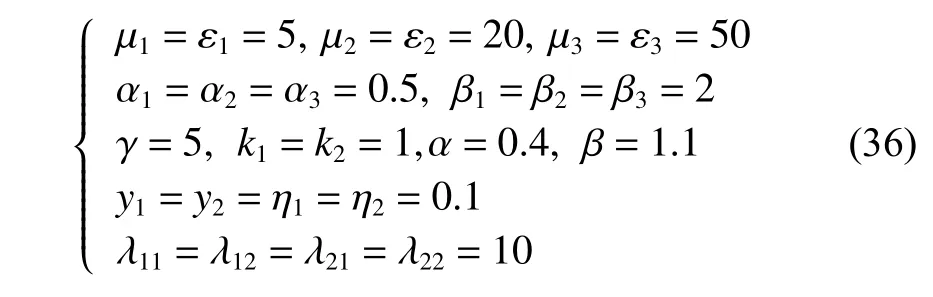
底栖式AUV 的目标位姿 ηd以及受到的环境干扰 τd为

4.1 观测器仿真
对观测器进行仿真,验证观测器的观测效果。仿真结果如图3~图5 所示。
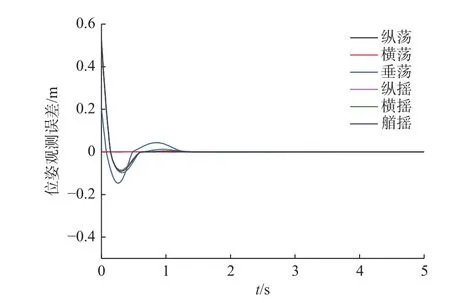
图3 位姿观测误差曲线Fig. 3 Curves of position and posture observation error

图4 速度观测误差曲线Fig. 4 Curves of velocity observation error

图5 集中扰动下的观测误差曲线Fig. 5 Curves of observation error with lumped disturbance
由图可以看出,本文使用的WCFTESO 观测器在不需要速度信息的情况下,仅依靠位姿信息即可在非常短的时间内精确观测出AUV 的位姿、速度以及集中扰动,且收敛时间在4 s 以内。因此,可以将观测值代替实际值进行点镇定控制器的设计。
4.2 点镇定控制跟踪性能对比仿真
不难发现,将式(24)中 α, β的值设为1 时,固定时间控制器就变为传统的渐近控制器。为了验证本文所设计固定时间控制器的控制性能,本节将固定时间控制方案与渐近控制方案进行了对比仿真,结果如图6~图10 所示。
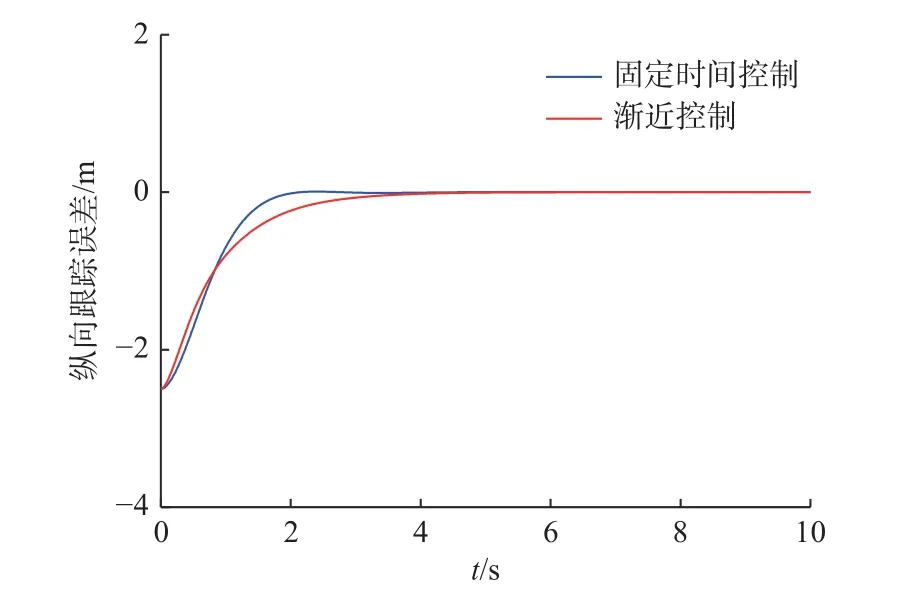
图6 纵向跟踪误差响应曲线Fig. 6 Respose curves of longitudinal tracking error

图7 横向跟踪误差响应曲线Fig. 7 Respose curves of transverse tracking error

图8 垂向跟踪误差响应曲线Fig. 8 Respose curves of vertical tracking error

图9 俯仰角跟踪误差响应曲线Fig. 9 Respose curves of pitch tracking error

图10 艏向角跟踪误差响应曲线Fig. 10 Respose curves of heading tracking error
由图6~图10 所示的AUV 位姿误差响应曲线可以看出,两种控制方案均能在一定的时间内收敛至稳定状态,且位姿误差收敛至0 后均能保持较好的稳定性,但两者在收敛速度上存在明显的差异。虽然渐近控制器在初始阶段的收敛速度快于固定时间控制器,但固定控制器最终收敛于0的时间在各个自由度均优于渐近控制器。其中,由图8 和图9 中曲线可以看出出现了一些波动现象,这是由多自由度控制时的耦合效应所产生,并不会影响控制系统整体的收敛性。
综上所述,本文所设计的固定时间反步点镇定控制器的控制性能要优于传统渐近控制器。
5 结 语
本文设计了一种基于固定时间扩张状态观测器的固定时间反步点镇定控制器,解决了受未知干扰以及不确定性影响的底栖式AUV 的点镇定控制问题。仿真结果表明,本文所设计的控制器在不需要AUV 的精确模型以及部分系统状态的前提下即可实现对其余状态变量及集中扰动的观测,并且观测误差会在固定时间内收敛,这对AUV在部分传感器未装配或者故障后的精确控制将起到至关重要的作用。同时,与传统的渐近控制策略相比,本文所提固定时间反步控制方法的收敛时间更短,这对以海洋石油勘探为背景的底栖式AUV 而言,也是不可或缺的。

