推进剂粘弹性对固体火箭飞行模态特性的影响①
夏 鹏,侯凯宇,史晓鸣,高 阳,孙晓娇,刘维丽,康海峰
(1.上海机电工程研究所,上海 201109;2.上海航天技术研究院,上海 201109;3.上海航天动力技术研究所,上海 201109;4.上海航天精密机械研究所,上海 201600)
0 引言
固体火箭发动机作为火箭的动力装置,同时也是结构的主要组成部分,近年来固体火箭发动机朝着高能化、轻质化的目标不断发展。然而,在此过程中,国内各研究单位陆续出现了发动机工作中不稳定燃烧问题,目前该问题已成为制约固体火箭发动机发展的重要技术难题。对于发动机不稳定燃烧机理,国内外已开展了大量研究,普遍认为该问题是由燃烧室声学振荡与燃烧过程中涡脱落相互耦合造成的。然而,BLOMSHIELD和MONTESANO等研究表明,发动机结构与燃烧室声腔的耦合振动也是引起发动机不稳定燃烧的诱因之一,与声涡耦合造成的不稳定燃烧研究相比,结构与声腔耦合造成不稳定燃烧研究相对空白。
对于固体火箭发动机结构模态试验和仿真分析,国内外学者已开展了大量研究工作。任萍等对空载发动机开展了模态试验并应用有限元软件进行了模态计算,由试验与仿真模态频率与振型MAC值(Modal Assurance Criterion,模态置信系数)可说明计算结果与试验结果之间有较好的相关性。孙海文等对采用发动机的某型火箭进行了整箭有限元建模分析及地面模态试验。VIVO等使用工况模态分析方法对VEGA火箭飞行状态下的模态特性进行了分析,分析结果与自由-自由状态下火箭仿真分析结果有高度一致性。KOHSETSU考虑到固体推进剂的不可压缩性,对发动机壳体和推进剂进行有限元建模,构建了固体火箭发动机轴向振动数学模型,并求解得到了火箭轴向振动模态。以上所述的研究中,学者们仅在线弹性范围内研究发动机内部的固体推进剂对固体火箭整体振动模态特性的影响。实际上,固体推进剂是一种高分子聚合物,其具有高质量分数的粘合剂组分,一般能够发生大变形,并且呈现出明显的粘弹性特性。任萍等认识到推进剂模量具有频变特性,并分析了推进剂模量变化对发动机结构弯曲、呼吸模态的影响,但其工作忽略了推进剂的粘性。张冬梅等指出推进剂具有复频变模量,介绍了一种混合梁模型建模方法,根据虚功原理对粘弹性复合结构进行了直接频响分析,但直接频响分析计算消耗大,不适用于真实固体火箭发动机的复杂结构。王哲君等从固体推进剂的力学性能实验测试方法、力学性能参数的确定以及本构模型的建模三方面对当前研究进展和不足进行了总结。李天鹏等对具有粘弹性固体推进剂在储运过程中受到温度载荷、振动载荷作用下的动态响应计算及其对结构完整性的影响进行了总结。
本文针对固体火箭模态特性分析研究中未考虑固体推进剂粘弹性影响的问题,开展考虑推进剂粘弹性的固体火箭模态特性分析研究工作。通过动态热机械分析(DMA)试验测量推进剂复频变模量,提出一种考虑推进剂频变模量的结构模态特性有限元迭代计算流程,采用模态应变能法对复合结构的阻尼特性进行分析,以空载、满载火箭模态试验数据验证了仿真分析方法的准确性,最后对推进剂粘弹性对火箭结构模态特性影响规律进行总结。应用本文所提出的方法,可有效提升箭体动力学建模的准确性,并提升了固体火箭在飞行过程中实时振动响应分析及故障排查的能力。
1 动态热机械分析试验
动态热机械分析(又称为动态力学分析,Dynamic Mechanical Analysis,DMA)是指测定在周期性振动应力下,材料随时间、温度和频率变化而变化的力学性能和阻尼性能。具有粘弹性的材料其剪切模量可表示为
=+
(1)
式中、、分别为阻尼层材料的复剪切模量、储能模量和耗能模量。
储能模量和耗能模量之间有如下关系:
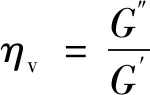
(2)
定义为阻尼材料的损耗因子,是材料在每个周期运动中损耗的能量与最大弹性储能之比。
采用METTLER TOLEDO DMA/SDTA861e设备,根据固体火箭发动机储运的环境温度,分别对丁羟推进剂开展低温-45 ℃、常温25 ℃以及高温60 ℃情况下1~1000 Hz频率扫描测试,频率间隔为10 Hz,试验采取剪切模式进行测量,测量该型推进剂的剪切储能模量及耗能模量,测量方法为强迫非共振法。试验常温情况下测得的推进剂随频率变化的材料特性参数如图1、图2所示。
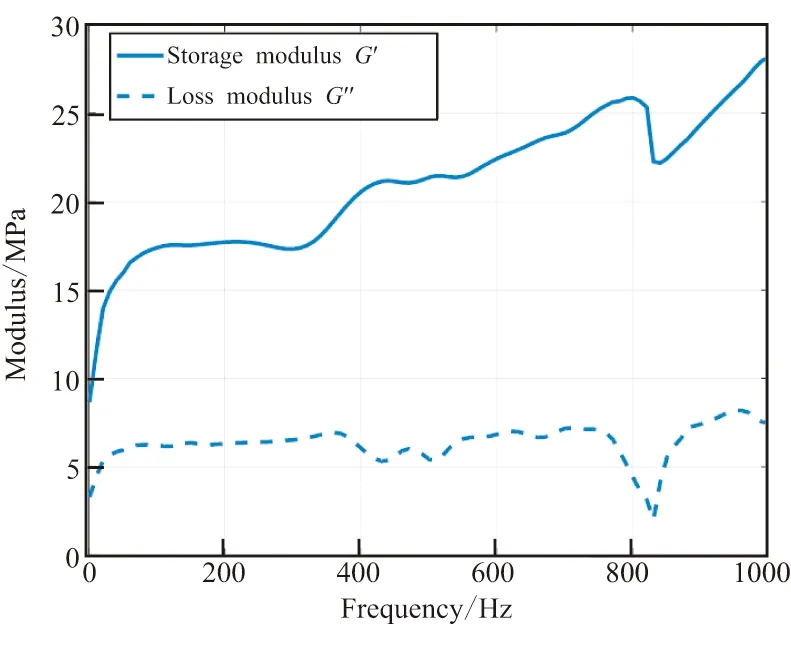
图1 剪切模量随频率的变化Fig.1 Variation of propellant shear modulus with frequency

图2 损耗因子随频率的变化Fig.2 Variation of propellant loss factor with frequency
2 模态应变能法
模态应变能法(Modal Strain Energy,MSE)因计算简单、快速而被广泛用于含阻尼层结构的建模与仿真分析中。已知单元节点位移与应变之间的关系及应力与应变的关系分别为
=u
(3)
=ε
(4)
式中为几何矩阵,为弹性系数矩阵。
单元的应变能可以表示为
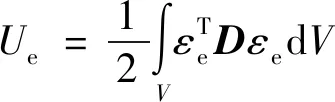
(5)
采用实特征向量表示含阻尼层复合结构的应变能为

(6)
式中为整体结构的实模态向量;为结构的总体积。
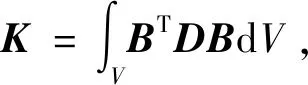
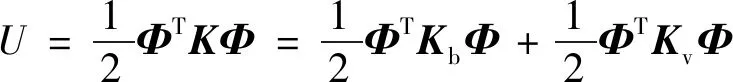
(7)
阻尼材料的耗散能表示为

则由模态应变能表示的结构模态损耗因子的表达式为
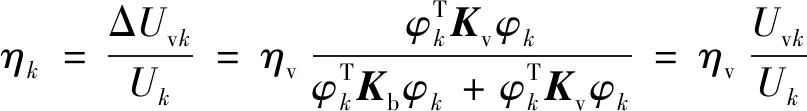
(8)
式中为含阻尼层复合结构第阶模态损耗因子;v为阻尼层的第阶模态应变能;为整个结构的第阶模态应变能,阻尼层第阶模态应变能v和结构第阶模态应变能可直接在有限元模态分析结果中提取。
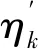

(9)
式中()为每阶固有频率下的阻尼材料的损耗因子。
根据阻尼特征值间的相互转换关系,含有含阻尼层复合结构的各阶模态阻尼比可表示为
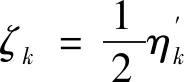
(10)
3 固体火箭模态试验
3.1 试验状态及测点
火箭安装示意图如图3所示,火箭由前后两个弹性橡皮绳进行悬吊,调整前后悬吊高度使火箭保持水平从而模拟自由-自由边界。弹性绳和箭体组成的悬挂系统,其悬挂频率满足航天行业标准QJ3285A—2018中6.3节的规定,安装后的模拟系统的刚体运动频率小于参试结构一阶弹性固有频率的1/6。
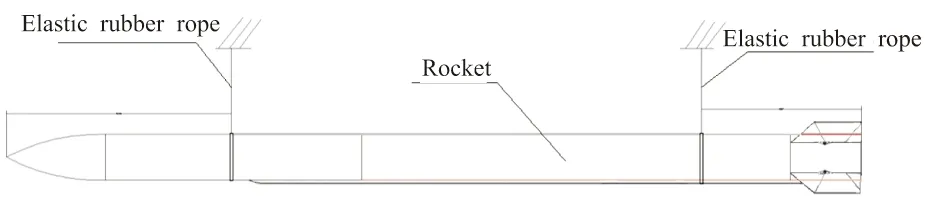
图3 火箭安装示意图Fig.3 Installation of solid rocket
试验采用多点激励多点响应测试方法,通过各点间的频响函数,使用PolyMAX方法识别模态参数。试验中使用B&K8206-002力锤产生激励,传感器采用PCB333B30振动传感器,信号采集与分析设备采用LMS SCR05-40。试验响应测点如图4所示,全箭沿向表面母线布置10个加速度响应测点,在发动机舱等距分布3个剖面,各剖面沿周向布置8个加速度响应测点,总计31个加速度响应测点,以此来测量火箭的全弹弯曲模态及发动机舱呼吸模态。
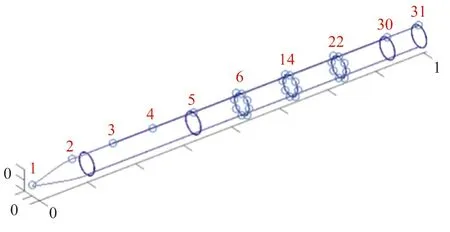
图4 测试设备响应测点布置Fig.4 Response measuring points arrangement
3.2 试验模态参数辨识结果
模态试验的模态参数辨识结果如表1所示,振型如图5所示。

表1 火箭模态参数Table 1 Modal parameters of the rocket
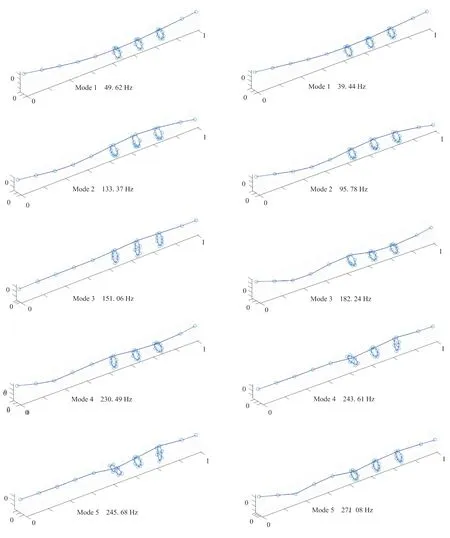
(a)Unloaded rocket (b)Full-loaded rocket图5 火箭模态振型Fig.5 Modal shapes of the rocket
4 固体火箭模态特性仿真
4.1 有限元建模
固体火箭发动机壳体采用高强度钢,推进剂采用内孔装药,尾部开有翼型槽。本文算例中的固体火箭采用“设备舱一维梁+发动机舱三维实体+药柱三维实体”的混合建模方式,设备舱段根据舱段材料和舱壁厚度简化为一维梁模型,根据箭上各设备质量质心,计算设备质心至梁单元两端节点的距离,根据杠杆原理将设备质量分配到两端节点上;舱段之间设置弹簧模拟舱段之间的连接刚度,连接刚度参数由工程经验和试验辨识得到;发动机壳体和推进剂药柱采用实体单元建模,发动机壳体与药柱单元接触界面上的节点满足位移协调与力的平衡条件。全箭有限元模型如图6所示,药柱的剖面如图7所示。

图6 全箭有限元仿真模型Fig.6 Meshing of FEA modal

图7 推进剂药柱剖面Fig.7 Propellant grain profile
4.2 仿真计算流程
粘弹性材料的弹性模量随频率不断变化,因此不能像弹性材料那样直接计算。本文采用有限元方法进行不断迭代,当满足阈值要求后,可认为迭代结果为合理值,本文阈值取0.1 Hz。再根据式(9)得到结构的模态损耗因子,从而得到模态阻尼。其计算流程如下:
(1)取推进剂准静态模量,对固体火箭结构进行实模态计算;
(2)根据上一步的模态频率的计算结果以及DMA试验中得到推进剂频变模量,修正各阶模态模型的推进剂模量;
(3)对修正后各阶模态模型进行实模态计算;
(4)若步骤(3)计算得到的该阶模态频率与上一步得到的模态频率变化小于设定阈值,则迭代停止;若大于阈值,则重新开展计算步骤(2);
(5)根据迭代模型实模态计算结果,输出每阶模态推进剂单元的模态应变能与结构总模态应变能;
(6)计算每阶模态下推进剂与整体结构应变能的比值;
(7)根据DMA试验结果,得到每阶固有频率下推进剂的损耗因子;
(8)根据式(9)计算得到结构模态损耗因子,并得到模态阻尼比。
4.3 固体火箭模态特性仿真计算
在有限元软件MSC.Nastran中对上述有限元模型进行自由-自由状态实模态计算,模态计算采用Lanczos方法,模态振型采用质量归一化。空载固体火箭由于无推进剂装药,因此直接得到模态信息,满载固体火箭通过计算步骤1~4迭代得到各阶模态信息。由于结构具有一定的轴对称特性,因此模态计算结果均为成对出现,本文只考虑沿箭体坐标系轴方向的模态,前5阶模态频率仿真计算结果如表2、表3所示,其模态振型云图如图8所示。

表2 空载火箭模态频率仿真计算结果Table 2 Unloaded SRM modal frequency simulation results

表3 满载火箭模态频率仿真计算结果Table 3 Full-loaded SRM modal frequency simulation results
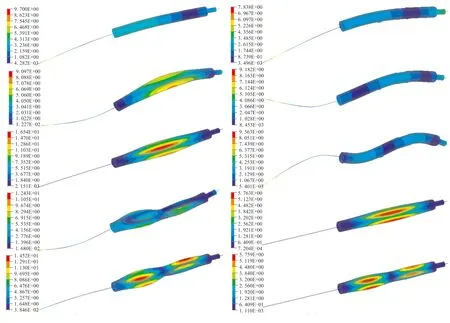
(a)Unloaded rocket (b)Full-loaded rocket图8 火箭模态振型仿真结果Fig.8 Modal shape simulation results of the rocket
从表2、表3空载、满载火箭全箭模态仿真计算与试验结果的对比中可看出,全箭前几阶模态频率、模态振型与试验结果吻合较好,说明本文采用的“设备舱一维梁+发动机舱三维实体+药柱三维实体”的混合建模方式和对满载火箭采用的有限元迭代计算方法是合理有效的。
观察空载火箭全箭二阶、三阶弯曲模态振型可以发现,当弯曲振型局部最大、最小值位于发动机舱时,会引起该位置截面形状发生改变,截面从圆变为非圆截面,其包围面积随着改变。然而,满载火箭二、三阶弯曲模态振型发动机舱截面形状未发生明显改变(如图9所示),这是由于内部推进剂装药提供了支撑刚度抑制了局部的变形。当接近空载状态的火箭在飞行过程中激励起全箭二、三阶弯曲模态和发动机舱呼吸模态时,发动机舱的截面振荡变化可引起发动机内部燃烧室的体积振荡变化从而造成压强振荡,对发动机内部燃烧过程产生不利影响。
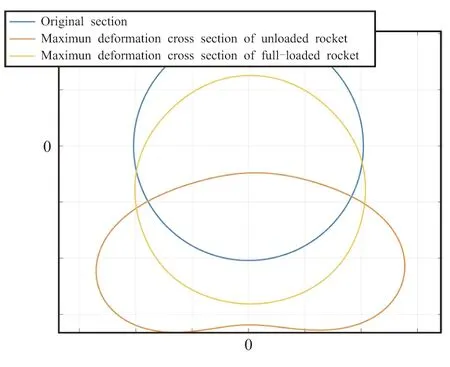
图9 空、满载火箭二阶弯曲模态振型发动机 舱横截面形状变化Fig.9 Shape change of motor section in 2nd bending modal shape of the unloaded &full-loaded rocket
4.4 满载火箭模态阻尼比计算
根据计算步骤5~8可得到各阶模态阻尼比,本文计算时涉及的相关参数如表4所示,各阶模态频率下的推进剂损耗因子由试验结果线性插值得到。
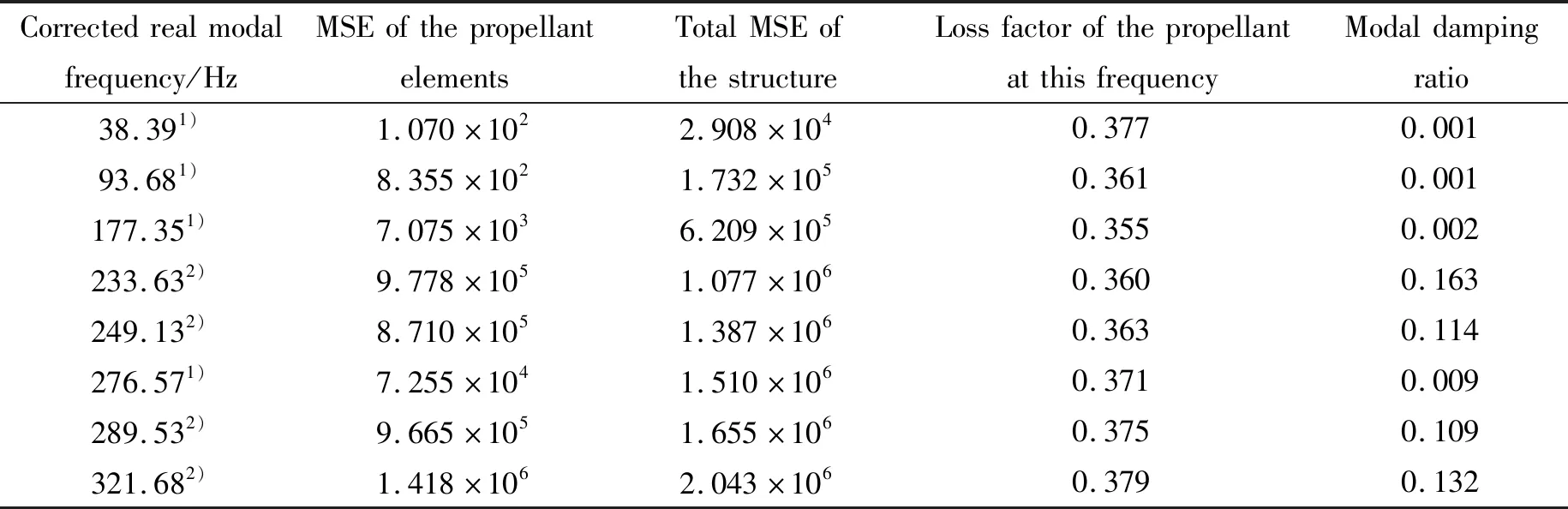
表4 满载火箭模态阻尼比计算Table 4 Modal damping calculation of the full-loaded rocket
从满载火箭模态阻尼比计算结果可看出,对内孔装药的固体火箭发动机,推进剂粘弹性对全箭弯曲模态影响较小,但能够明显提升发动机舱呼吸模态的阻尼比。当推进剂装药厚度随着燃烧逐渐变薄,推进剂的整体粘弹性效应会逐渐削弱,发动机呼吸振动幅值也随之变大。
4.5 固体火箭频响函数仿真分析
在发动机壳体末端(对应试验测点30)沿向施加一个单位脉冲激励,提取前箭身二分位置(试验测点3)梁单元、发动机舱四分位置(试验测点6、14、22)向上表面实体单元的加速度频响函数。计算方法采用模态法,满载火箭各阶模态阻尼比由模态应变能法计算得到,由于全箭为金属结构,空载火箭不含有粘弹性推进剂,因此各阶模态阻尼比取工程经验值。计算考虑前60阶模态,计算结果输出范围0~500 Hz。仿真分析得到的频响函数曲线与试验测得的频响函数曲线对比如图10~图13所示。
(a)Unloaded rocket (b)Full-loaded rocket图10 试验测点3仿真计算结果Fig.10 H(ω) simulation results of No.3 test point
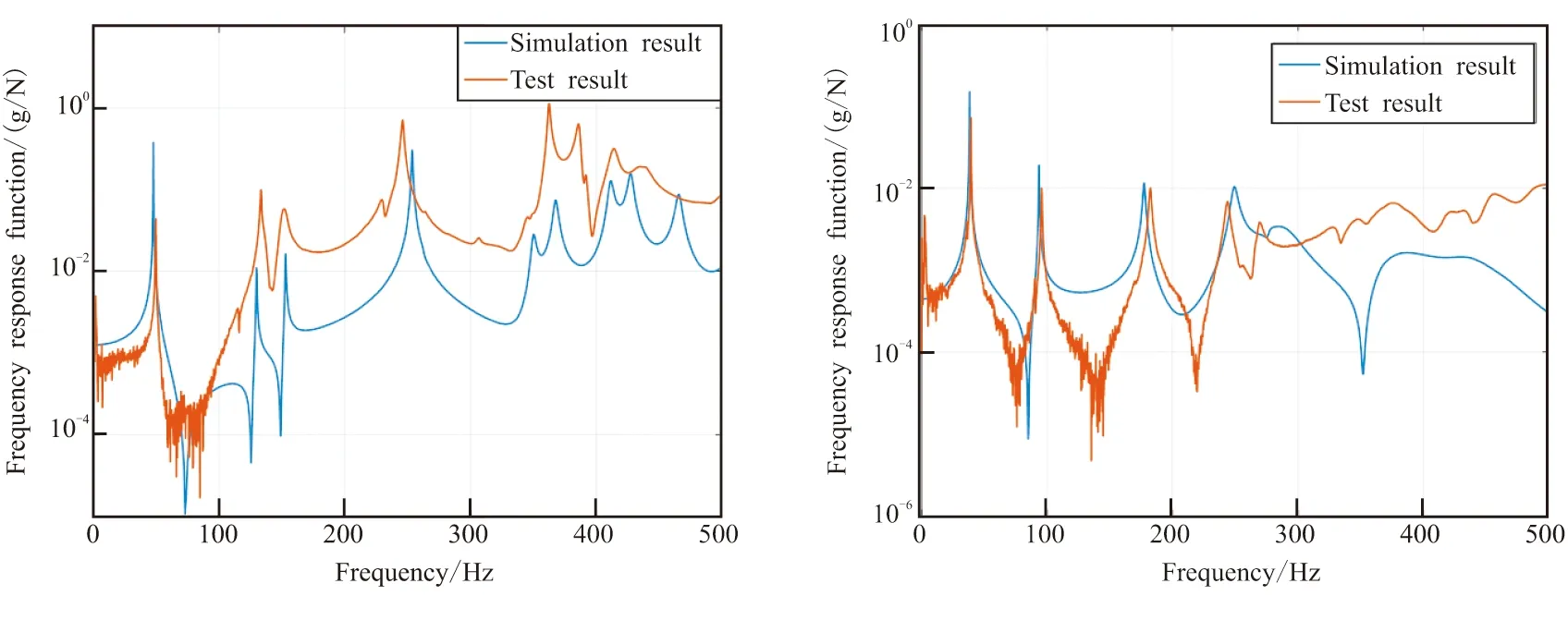
(a)Unloaded rocket (b)Full-loaded rocket图11 试验测点6仿真计算结果Fig.11 H(ω) simulation results of No.6 test point
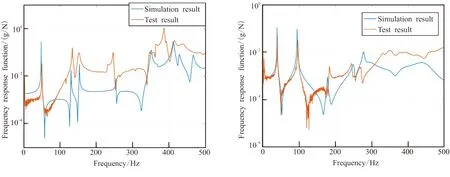
(a)Unloaded rocket (b)Full-loaded rocket图12 试验测点14仿真计算结果Fig.12 H(ω) simulation results of No.14 test point
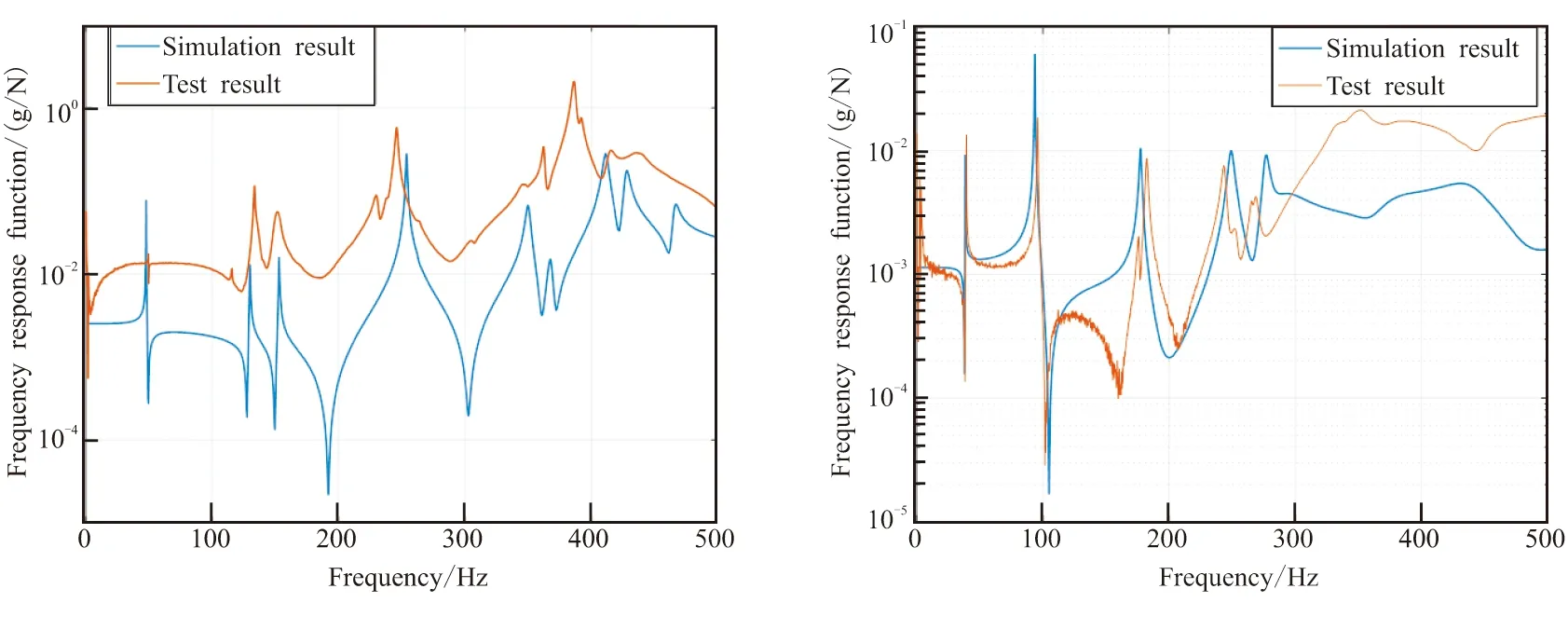
(a)Unloaded rocket (b)Full-loaded rocket图13 试验测点22仿真计算结果Fig.13 H(ω) simulation results of No.22 test point
从空载火箭测点6、14、22频响函数曲线中,可明显看到发动机舱呼吸模态振动引起的峰值,而满载火箭频响函数中主要是全箭弯曲模态引起的峰值。这是由于推进剂肉厚较厚时,其粘弹性特性所提供的阻尼效应抑制了呼吸振动变形。使用频变模态应变能法得到的满载火箭频响函数仿真分析结果与试验测试值吻合较好,但发动机舱上三个测点在高频部分有较多的鼓包和峰值。这是由于仿真分析中对发动机药柱构型进行了简化,而试验采用真实发动机,其内部复杂的装药导致高频部分存在较多推进剂局部模态。
5 结论
(1)对于大长径比的固体火箭,推进剂刚度会影响发生弯曲振动时截面变形,当推进剂装药厚度随着燃烧逐渐变薄,在本文算例中,肉厚与火箭半径的比值从65.9%降低至0%,推进剂提供的抗弯刚度逐渐减少,全箭在弯曲振型中出现发动机壳体截面变形逐渐增大的现象。
(2)推进剂粘弹性对发动机舱呼吸振动有明显的抑制作用,当推进剂装药厚度随着燃烧逐渐变薄,推进剂的整体粘弹性阻尼效应会逐渐削弱。以本文发动机舱二阶呼吸模态为例,由满载到空载的过程中,阻尼比从8.91%下降到0.43%,从而导致发动机呼吸模态的振动幅值也随之变大。
后续应进一步结合发动机推进剂燃面退移量,获取火箭飞行的实时推进剂装药构型,对任一工作时刻全箭模态特性进行分析,完善火箭工作过程中振动问题的分析及排查能力。

