基于LineMod的弱纹理多目标遮挡检测方法

蒋云飞柴 琦杨 杰

(青岛大学机电工程学院,青岛 266071)

近年来,机器人广泛应用于家居环境,尤其是拥有机械臂自主抓取功能的机器人,所以在机器人技术中必然要融入计算机视觉功能[1]。在抓取时,机器人面对的是不同大小、形状及位姿的生活物品,并且经常存在物品被严重遮挡的问题,这给机器人的目标检测任务带来较大的挑战。目前,针对复杂场景多目标重叠物体的识别研究成果并不理想。2011年Hinterstoisser等[2]提出了旨在解决杂乱场景中少纹理3D 物体的实时监测与6D位姿估计定位问题的第一代LineMod算法,适用于部分杂乱场景检测及工业上常见的少纹理或无纹理元器件的检测识别,但对于同种物体相互重叠等复杂情况下的物体分割识别仍存在一定的不足;2012年第二代LineMod算法选择较为稀疏的视角采样,采用分块匹配的思想提升被遮挡物体的打分[3],一定程度上解决了目标遮挡识别难题,但是识别准确率较低,分块匹配速度提升不明显,未从根本上解决遮挡问题;LCHF模型借鉴了LineMod的模板匹配功能以及霍夫森林投票方式,采用新型分割函数集成到回归森林的方式来处理严重杂乱和遮挡场景中的3D物体检测和位姿估计[4-5],但LCHF受限于手动标注特征,在解决识别多个物体以及重叠场景问题时效率较低;Patch-LineMod算法[6]利用Kmeans均值聚类方法将整个模板分割成不同的特征块,利用训练特征块与目标物体的点云相似性进行识别判断[7-8],提高了多目标重叠场景下的识别能力。但该方法采用的特征点分块方式极其简单,特征分类机制存在较高的错误匹配率及漏选率。针对LineMod算法不能对弱纹理重叠目标进行有效检测的问题,本文利用LineMod算法的原理,提出了一种基于7D特征的聚类匹配识别方法CMRL(Cluster-matching Recognition Improved LineMod),将特征点具有的更深层次的7D特征向量信息[9]作为分类影响因素,分析特征点信息的内部逻辑,提高独特特征在特征点分类过程中的影响比重,结合Kmeans均值聚类方法,利用新的特征点分类规则,完成特征点更加合理的聚类,形成包含更多匹配信息的特征模板,以便获取更加准确的匹配识别结果,从而提高多目标遮挡情况下的识别效果。

1 基于LineMod的聚类匹配识别方法

在Line Mod算法基础上,本文引进7D 特征向量,取代原有的3D 空间向量。7D 特征向量包含3D 空间位置特征向量(X、Y、Z)以及4D 位姿向量(梯度方向Rgd、梯度幅度Rgm、表面法向量方向Rsd、表面法向量幅度Rsm)。在计算特征信息时,各特征点受到7D 特征向量的影响,能获得更加合理的特征块,可以很好地分离物体表面具有明显相关性的特征,使获得的模板更加具有逻辑相关性和可识别性。在特征信息降维的过程中,本文采用梯度下降法,将包含7D 特征向量的特征信息降维为3D,之后采用特征点均值聚类实现模板的总匹配,同时自动消除多余的聚类,至此获得具有大量独特特征信息的新特征模板,在匹配过程中可以明显提高识别精度。

1.1 计算特征向量

特征点的7D 特征向量处理过程如图1(a)、(b)所示,输入物体的原始点云数据后,通过计算每个3D 特征点的4个附加特征向量形成如图1(b)所示的7D 特征向量。

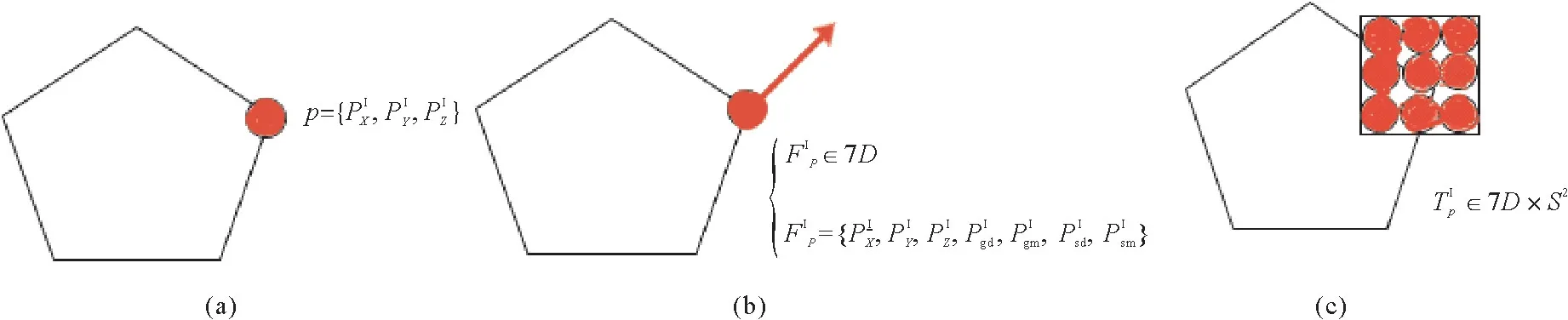
图1 7D特征向量处理过程和形成特征块过程

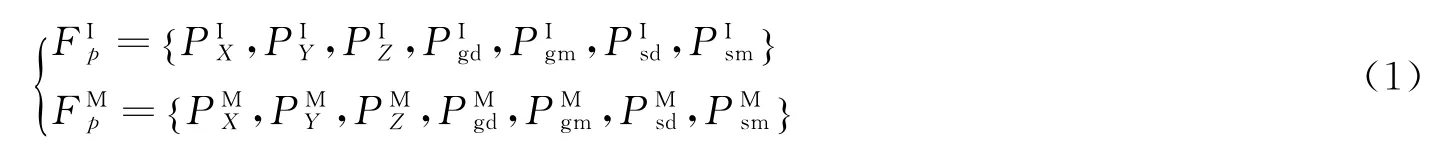
1.2 计算特征块

获取7D 特征向量后,需要对模板进行分块处理。设定特征尺寸s,然后集成特征点邻域s×s区域内的特征点作为待匹配特征块,图1(b)、(c)所示为模板信息处理形成特征块的过程。

特征块计算

其中,p是特征块T 的中心点,s×s以p为中心点的邻域。

1.3 降维计算新的3D特征向量

降维计算是利用数据降维算法将7D 特征向量信息降维为3D 特征信息,实现特征信息的可视化,便于分类计算形成新的3D 特征向量[10],具体过程如图2所示。

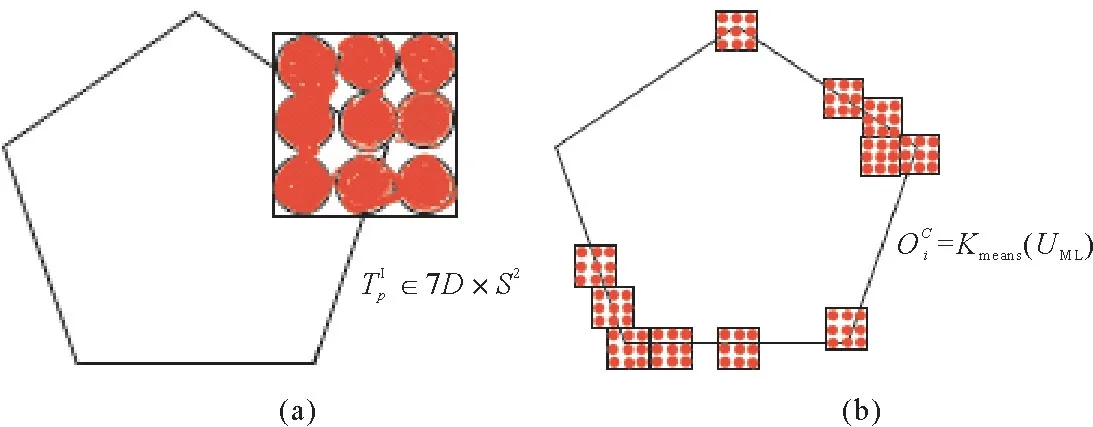
图2 Kmeans 均值化计算新的3D向量过程

本文借鉴无监督降维算法(Principal Components Analysis,PCA)、随机近邻嵌入算法(Stochastic Neighbor Embedding,SNE)及t分布随机近邻嵌入算法(t-distributed Stochastic Neighbor Embedding,t-SNE),采用Kmeans均值化方法获得新的3D 空间特征向量,实现高维数据空间映射为低维数据空间的非线性降维[11]。函数输入为式(1)的7D 特征向量,输出为优化后的新的3D 特征信息I,向量降维函数UML()为

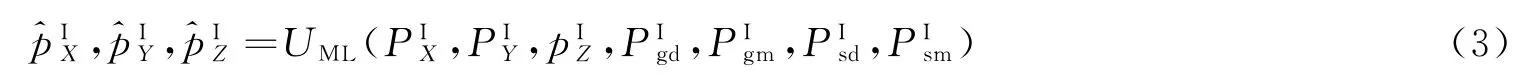
UML()函数类似于t-SNE算法,可以很好的解释不同特征之间的复杂多项式关系以及分析聚焦于低维区域中不相似的数据点之间的关系,并保留原有的重新分块得到的特征块信息。

为了更好地解释UML()函数,采用t-SNE算法[11]表示

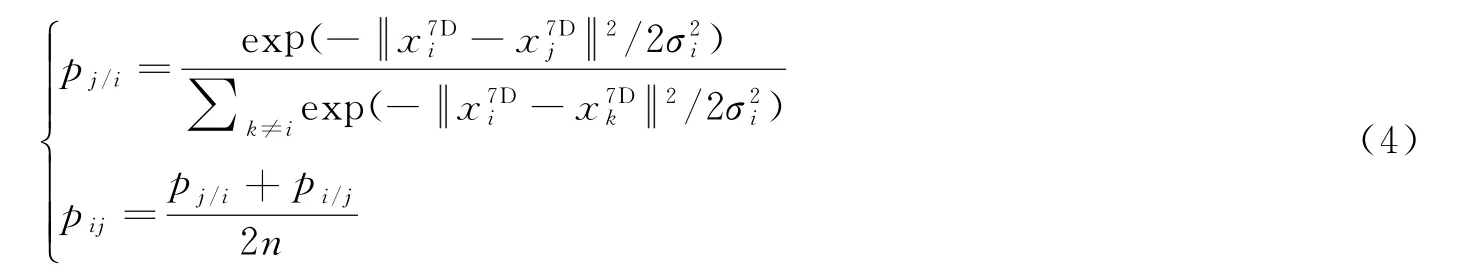
在3D 空间高低映射过程中,条件概率q ij用以反映高维空间7D 特征向量和低维空间3D 特征数据点之间的相似性

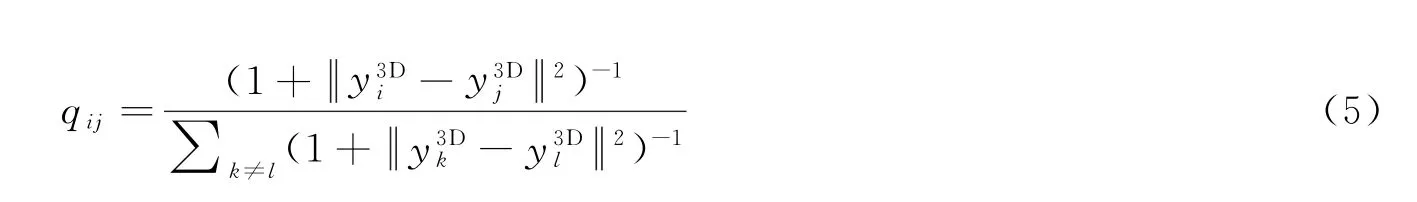
利用式(4)、式(5)计算7D 空间内所有特征点的条件概率p ij和q ij,代入计算其对应的KL()散度(Kullback-Leibler Divergence),得到散度最小值对应的两条件概率。KL()散度衡量两个概率分布之间的距离,值越小表示两个条件概率值越接近,即新的3D 空间的条件概率分布与真实的7D 空间条件概率分布越接近,完成了特征块信息完整映射降维。计算相似度

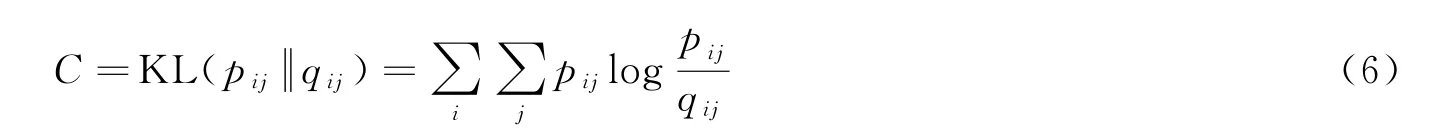
之后利用随机梯度下降法[12]完成7D 特征向量向3D 空间的特征信息映射

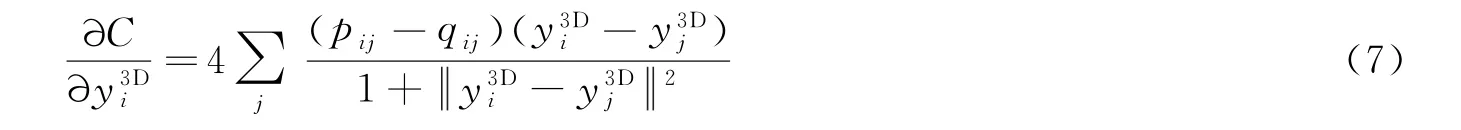
经过对条件概率p ij和q ij的反复计算获得最佳的相似度,最终得到从映射到3D 空间的特征信息。

1.4 计算新的特征模板

本文提出的CMRL算法借助于引进的7D 特征向量,用新的特征信息替代单纯的特征点空间信息进行特征块的聚类匹配,获得新的特征模板

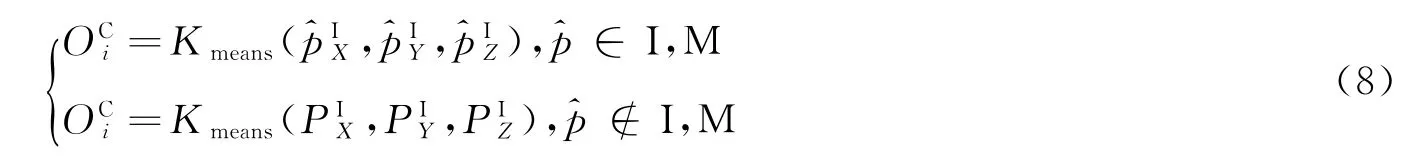
其中,O i代表特征块信息,代表了基于Kmeans聚类在特征聚类生成过程中所使用的模板聚类方法。

这样可以充分利用特征点的内在逻辑关联性来提高物体独特特征(物体边缘、角、圆弧等)对特征点分类影响的比重,从而获得关联性更强的新的特征模板,具体过程如图3所示。

图3 新特征模板分块聚类的过程

图4所示为模板的原始特征点以及分类后的实际模板聚类结果。

图4 模板聚类结果

1.5 计算匹配度及6D位姿估计

利用余弦相似度函数Sim()测量两个输入向量的角度,在输入的图像中由pose()函数得到与训练数据集中模板最接近的最大相似度模板特征,特征模板包含目标对象已训练的位置信息,将新的特征模板与测试图像比对匹配,从而完成目标物体的识别与6D 位姿估计过程。

具体的匹配识别及位姿估计过程如图5所示。利用非极大值抑制算法进行位姿计算、校正及验证,即通过ICP(the Iterative Closest Point)后处理算法,依据相似度分数去除位姿估计过程中得到的重复的或错误的位置信息,并采用校正验证以提高位姿估计准确度[13]。

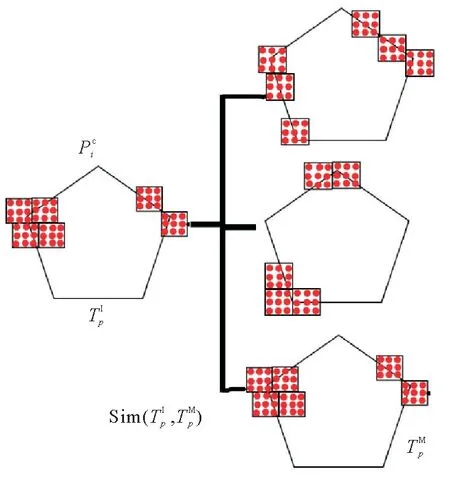
图5 目标检测与位姿估计过程示意图

2 实验与结果分析

现用实验验证CMRL 方法在应对复杂场景重叠物体时的目标识别效果。实验条件设置:CPU 为Intel(R)Core(TM)i5-9300H＠2.40GHz,内存16GB,借助Kinect V2 Depth传感器,使用Doumanoglou数据集。Doumanoglou数据集是针对复杂场景中测试多目标重叠物体的识别算法与位姿估计能力的公用数据集,包括训练集和测试集两部分,与LineMod算法的训练识别过程刚好吻合。为清晰表示CMRL方法针对复杂场景重叠物体的识别效果,本文采用召回率和F1值来表示,F1值表示算法识别结果与真实场景中所有结果的匹配度。

图6为部分实验过程。实验在152个测试样本上开展,Line Mod、Patch-Line Mod、CMRL算法在场景1(咖啡杯)、场景2(果汁盒)及场景3(两种物体混合)的召回率结果见表1。可知,Line Mod算法不具备复杂场景下重叠物体的识别能力,平均召回率仅10.6%。在场景1(咖啡杯)和场景2(果汁盒)中,Patch-Line Mod算法和CMRL算法均展现了较为出色的重度遮挡情况下多目标物体的识别能力,其中CMRL算法的识别能力更为出色。

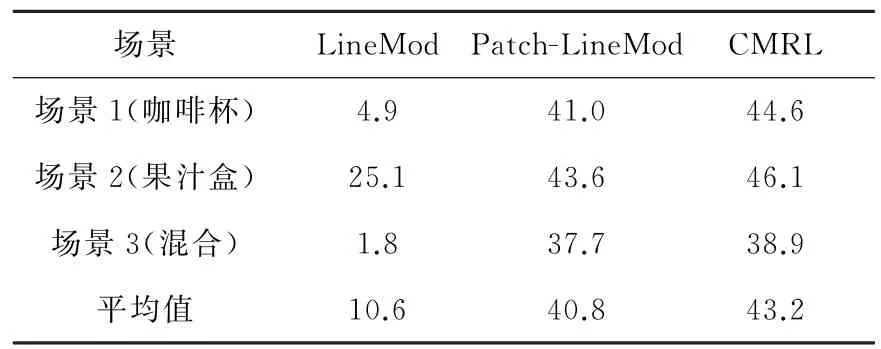
表1 LineMod、Patch-LineMod、CMRL方法在3种场景下召回率(%)

图6 目标检测实验结果

对比不同的经典算法在Doumanoglou数据集上Ntop＝1(最高自信度的目标)时的F1分数,结果见表2。Ntop值指在所有估计值中具有最高自信度的前N个估计值。分别测试了Line Mod算法、PPF(点对点特征)算法、Hough-Forest算法、Doumanoglou算法和CMRL方法的F1值,平均值为该算法在两个数据集性能的平均F1值。

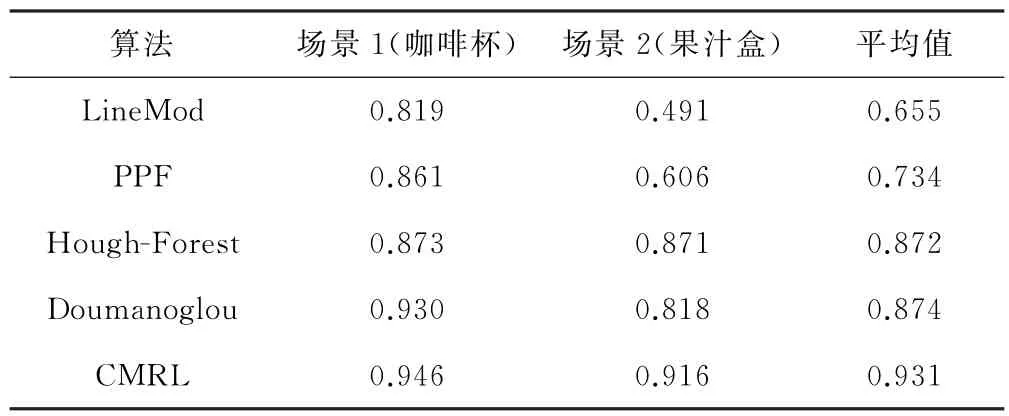
表2 各算法Ntop=1时在场景1和场景2的F1分数

Ntop＝1时,CMRL算法在两个场景下的分值最终达到了0.946和0.916,证明该方法的识别准确率大大提高,平均水平达到0.931。场景2中,CMRL算法的F1分数相较于其他算法有了明显的提高,说明本方法具备更高的识别准确度以及更出色的识别能力。

3 结论

本文提出的CMRL 方法在面对多目标遮挡复杂情况时展现了较好的目标检测能力,相较于Line Mod算法,在鲁棒性、识别率和准确度等方面都有了明显提升。但限于实验条件和时间问题,只在Doumanoglou数据集上进行了仿真验证,并未在实际场景中进行测试,日后可以尝试在更多数据集场景下进行仿真或者在实际场景中进行实验验证。