基于互信息的属性约简改进算法

朱 琦刘遵仁李书达

(青岛大学计算机科学技术学院,青岛 266071)

粗糙集是波兰数学家Pawlack于1982年提出的一种数学思想,用来对不确定性知识进行分类[1-2],广泛地用于机器学习、决策分析、数据挖掘等众多领域[3],并在相关研究中衍生出决策粗糙集、模糊粗糙集、邻域粗糙集等不同方向,扩展了粗糙集理论的应用场景[4-7]。属性约简是粗糙集理论的核心思想,在保持原始信息系统、知识库或决策表分类能力不变的情况下,用以删除知识表达系统中的冗余或不重要的知识,简化原有系统,并从中提取出相关知识和有用知识。基于互信息的属性约简算法将传统的属性重要度算法作为度量标准对条件属性进行筛选,但此算法不能保证得到决策表的最小属性约简[8-10]。针对于传统属性约简算法的缺陷,相关研究提出了许多改进算法,一定程度上提高了传统算法的效率和准确性,但仍有不足之处[11-12]。如,考虑到单个属性与其它属性间依赖关系的改进属性重要度算法,每次计算条件属性时都要对其它所有的条件属性进行判断,增加了算法的时间复杂度[13];文献[14]对传统算法中重要度定义算法做出相关改进,但并不能判断出哪一个属性重要度更高;针对决策类粗糙集提出的局部视角方法并不适用于所有的决策类属性约简[15];文献[16]提出决策规则的强规则和弱规则,生成非冗余规则,保留必要规则,删除不必要属性,但时间复杂度偏高;可变正区域的约简方法在属性约简时允许一定的程度变化,但泛化能力有待提高[17]。传统的粗糙集属性约简算法依然存在计算精度较差、准确率较低等问题,影响了粗糙集理论的适用范围和应用场景。借鉴已有研究成果,本文针对算法精度较差的问题,引入条件熵,将单个属性的重要度加入判断条件中;针对决策问题,引入了权重,用以度量互信息和当前条件熵之间的权重大小;在多个相关的数据集上测试本文算法可行性,并利用两种不同的分类器验证其准确性。

1 粗糙集理论概述

定义1正域[18-19]。知识Q相对于知识P的正域为,或称其为知识Q的P-正域,记为posP(Q)。

定义2知识的相对约简[18]。给定一个知识库K ＝(U,S)和知识库上的两个等价关系P,Q⊆S,对任意的G⊆P,若G满足以下条件:

(1)G是Q独立的,即G是P的Q独立子族;

(2)posG(Q)＝posP(Q);

则称G是P的一个Q约简,或称为G是P相对于Q的一个约简,记为G∈REDQ(P)。其中,G∈REDQ(P)表示P的全体Q约简组成的集合。

定义3知识P的信息熵H(P)[20]。给定知识P概率分布,则称为知识P的信息熵,简记为H(P)。

定义4知识Q相对于知识P的条件熵H(Q|P)。给定知识P和Q以及各自的概率分布和条件分布,则为知识Q相对于知识P的条件熵,简记为H(Q|P)[21]。

定义5知识P与Q的互信息I(P;Q)。给定知识P和Q以及各自的概率分布和条件概率分布,则可得到信息熵和条件熵,称I(P;Q)＝H(Q)－H(Q|P)为知识P与Q的互信息,简记为I(P;Q)[21]。

2 改进的基于互信息的属性约简算法

2.1 属性重要度的定义

传统的属性约简算法,属性重要度计算公式为

计算时只考虑所选择的条件属性加入核属性集之后相对于决策属性的互信息,这种思想在加入当前条件属性计算后所得互信息相同时,并不能有效地判断加入哪一个条件属性可以得到最优的决策规则。绝大多数情况下传统算法可以得到决策表的一个属性约简,但不能保证得到决策表的最小属性约简。

本文提出了一种新的结合互信息和条件熵的度量方法,相比于传统算法,在计算属性重要度时加入了对条件属性本身条件熵的度量[22];考虑到每一个条件属性自身的信息熵对属性重要度的影响,选取自身信息量少的属性加入核属性集,从而得到相对最优的决策规则。

设决策信息表DT＝(U,C∪D,V,f),C是条件属性集,D是决策属性集,且有核属性集B∈C,对于任意非核属性c i∈CB的基于信息熵的重要性Sig(c i,B,D)定义为:在核属性集中和加入某个非核属性后的条件熵与该属性自身的信息量之比的差值

由Sig(c i,B,D)定义可知,属性重要度随着作为基数的属性自身的信息量H(c i)的增大而减小,因为当H(c i)大时,属性c i会有更多的不同值,从而导致最终的决策包含更多的规则,若要得到最优决策规则,应取H(c i)最小值(如若需要查看更多的决策信息而不求获得最优决策规则时,可选H(c i)最大值,需要注意的是,若决策表信息量很大时,所得决策规则会非常庞大)。相比之前的核属性,添加属性c i后,Sig(c i,B,D)越大,对决策属性的影响越大,属性c i就越重要。

2.2 算法执行过程

本文算法是基于互信息的决策表属性约简思想求得属性的相对约简。首先判断决策表是否相容,若不相容,需进行处理,具体方法见文献[23]。继而得到决策表的差别矩阵,由差别矩阵可以快速分析出决策表的核属性,之后进行非核属性的属性约简:每次从非核属性集中选取Sig(c i,B,D)值最大的属性加入和属性集,同时分析是否满足I(B,D)＝I(C,D),满足则输出当前约简B,否则继续从剩余非核属性集中选取属性重复上述计算,直到满足I(B,D)＝I(C,D)的条件,结束计算。

Step1计算DT 中条件属性C和决策属性D的互信息:I(C,D)＝H(D)－H(D|C);

Step2计算C相对于D的核Core(B);

Step3计算I(B,D)＝H(D)－H(D|B),若I(B,D)＝I(C,D),则跳转到Step 5,否则执行Step 4;

Step4对于所有的c i∈CB,计算式(2),求得maxSig(c i,B,D),令B ＝B∪{c i},转到Step 3;

Step5输出B即为所求,算法结束。

3 实例分析与实验测试

3.1 实例分析

为验证算法的有效性,选用气象状况实例表,见表1。其中,条件属性集C＝{a1(Outlook),a2(Temperature),a3(Humidity),a4(Windy)},决策属性D＝{N,P}表示分类。将属性值用英文首字母代替:a1＝{sunny(S),overcast(O),rain(R)},a2＝{hot(H),mild(M),cool(C)},a3＝{high(H),normal(N)},a4＝{false(F),true(T)}。

表1 决策表

Step1求矩阵M s(14×14),长度为1的元素包含的属性即为核属性,M s包含的核属性为B ＝{a1,a4};

Step2计算I(C,D)＝H(D)－H(D|C)＝0.94－0＝0.94;

Step3计算I(B,D)＝H(D)－H(D|B)＝0.94－0.34＝0.60≠I(C,D),则继续计算;

Step4计算式(2),取α＝0.9,Sig(c i,B,D)＝α[H(D|B)－H(D|B∪{c i})]－(1－α)H(c i)＝0.9×(0.34－0)－0.1×1.5566＝0.150,Sig(c i,B,D)＝α[H(D|B)－H(D|B∪{c i})]－(1－α)H(c i)＝0.9×(0.34－0)－0.1×1＝0.206;Sig(c3,B,D)＞Sig(c2,B,D),令B ＝B∪{c i}＝{a1,a3,a4};

Step5再次计算I(C,D)＝H(D)－H(D|C)＝0.94－0＝0.94＝I(C,D),输出B ＝{a1,a3,a4}即为所求。

利用传统判别函数式(1)计算得到B＝{a1,a2,a4}或B＝{a1,a3,a4},都可作为结果,因为传统判别函数在计算属性重要度时没有加入对条件属性本身条件熵的度量,在加入某个属性后得到的互信息相同时,算法即终止,无法作出进一步的判断。这就存在局限性,尤其是在面对数据集中的两个属性相近,或数据集庞大属性较多时,很难给出确切的属性约简,导致结果不够准确。而改进算法将B ＝{a1,a3,a4}做为最终的约简结果。因为改进算法在计算中加入了对单个属性自身条件熵的考量,在两个或多个条件属性加入计算时,可区分两个属性重要度大小,从而得出更精准的属性约简结果,获得更精简的决策规则。

3.2 实验测试

3.2.1 UCI数据集测试 在Intel Core(TM)i5－8500T CPU 和8GB内存PC计算机上,window10环境下运行Python 3.7进行实验测试。从UCI数据集中选取了6个数据集,验证算法的可行性。分别比较传统的CEBARKCC算法(记为算法A)和本文改进算法(记为算法B,α＝0.9)的约简结果和时间,时间取每个数据集执行10次的平均值。实验结果见表2。

表2 两种算法对数据集的测试结果

由实验结果可知,改进算法可以得到相对决策规则更少的正确的属性约简,且时间消耗与原算法接近,时间消耗稍多出来的部分是对H(c i)的计算,本文算法具有可行性。

3.2.2 选用分类器测试 为了验证改进算法约简出的属性集合的有效性,在两种不同的分类器Knn算法和决策树算法中分别验证。对CEBARKCC算法约简的属性集(算法A)、改进算法(算法B)约简的属性集进行分类精度验证,数据为100次测试结果取均值,结果见表3。

表3中两种分类器关于两种不同算法属性约简分类精度的折线图如图1、图2所示。算法B与算法A时间复杂度相同(算法B需计算H(c i),两算法最坏情况下均为O(n2)),但算法B能得到更优的属性约简规则。值得注意的是α的取值,以上测试均在α＝0.9时测得,在同一个数据集上,微调α会使算法B较算法A 有1%～5%左右的精度提升。当H(c i)被赋予的权重过高时,将导致不同的属性约简,数据的条件属性越多时差异会越大。考虑到用H(c i)信息熵当作参考数据,经测试一般取0.8≤α＜1比较适合。

表3 两种算法在不同分类器下对数据集测试结果

图1 两种算法在Knn分类器下的精度折线图

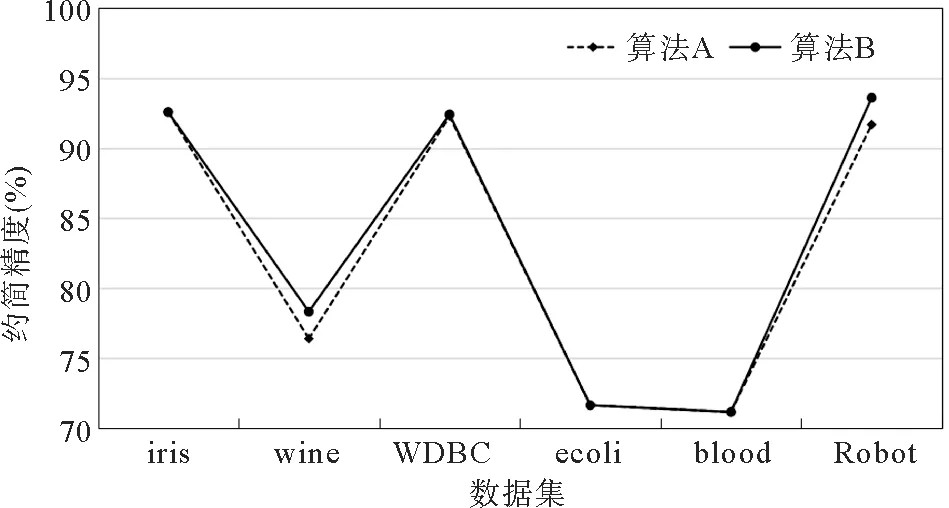
图2 两种算法在Tree分类器下的精度折线图

数据集属性数量过小或数据差别不大时,两种算法精确率大致相当。但在Robotnavigation数据集上,算法B在两种分类器上精度都有明显提升,因为当数据量较大时,数据的差异性也会增加,相较于算法A,算法B加入了对每个属性条件熵的判别,于是得到了更加精准的属性约简结果和更高的准确率。在实际应用中,数据集均包含大量数据,算法B便有更加明显的实际性能提升。因此,本文改进的属性约简算法可用于knn分类器和决策树分类器中,分类结果相对准确,具有可行性。

4 结论

本文从信息论的角度分析决策表属性约简问题,结合条件属性本身的互信息,提出了改进的属性约简算法。在保证时间复杂度不增加的情况下,本文改进算法相较于传统算法得到了更好的约简结果,在约简精度上有明显提升。通过对UCI数据集和分类器的测试,验证了改进算法的有效性。如何在不增加额外计算量的情况下得到更好的属性约简结果是今后有待解决的问题。