基于LTNE的饱和多孔介质THMC耦合模型数值研究

戴 倩， 李培超

(上海工程技术大学 机械与汽车工程学院， 上海 201620)

无论是生产还是生活中，多孔介质材料都十分常见，例如海绵、隔音泡沫及锂离子电池隔膜等。多孔介质是由固体骨架和孔隙空间组合构成的物质，孔隙一般由单相或多相流体共同填充。其研究和发展拥有较为悠久的历史[1]。为简单起见，前人采用了一些通俗而经典的物理模型进行研究，如圆环[2]、圆管[3-4]、平板[5]和无限大平面[6]等，以软件辅助模拟，用公式推导分析，大大促进了多孔介质理论的进步。

对于多孔介质的研究，大多集中于多物理场(诸如应力应变场、流场、温度场、电化学场等)耦合问题中。常见的有流固耦合[7-8]、热流耦合[9]和热流固耦合[10-13]等数学模型。但更完善的为热流固化耦合模型，常应用于生物医疗、海水入侵、水利工程和农田喷洒等领域。

诸多科研工作者对多孔介质热流固化耦合数学模型进行了深入探讨和研究。孔祥言[14]404建立了天然气水合物的部分耦合控制方程组，并考虑了渗透率和毛管力随饱和度的变化。Sun等[15]描述了热流固化耦合力学行为，将模拟结果与测试数据进行了对比和分析，验证新开发代码的实用性。盛金昌等[16]240着重考虑钻井过程中热流固化耦合过程和井壁孔隙压力、温度、应力和离子溶质摩尔分数等变化，提供了更加精确的井壁应力分布。

研究多孔介质多物理场耦合问题的传统假设大都是基于局部热平衡理论即LTE[17-18]，但当内部换热不均匀，固体骨架和孔隙流体的温度差值不可忽略时，局部热平衡理论不再适用，需运用更加合理的局部热非平衡理论即LNTE[19-20]来描述此类情形。例如，陈丽等[21]750基于LTNE理论和加权平均温度的概念，把握化学-热-孔隙弹性模型的特点，应用Laplace变换法对多场耦合表达式进行无量纲化，并与LTE条件的相关结果进行图像对比，发现LTNE效应在Biot数为中等范围内不可忽略。

前文所述的多物理场耦合方式，多为部分耦合或弱耦合。鉴于此，课题组假设多孔介质中的孔隙流体为溶质(NaCl)和溶剂(H2O)2种化学组分，构建更加完备的THMC强耦合数学模型。

1 数学模型

课题组将空间问题简化为平面问题，如图1所示。采用内含一半径a=0.1 m的圆孔无限大平面饱和多孔介质模型进行研究。其中，格子区域为饱和多孔介质无限大平面，表示以r的圆心为原点的径向坐标。简单起见，基本假设如下：①多孔介质为均匀且各项同性的介质，固体骨架变形符合小变形假设；②流体为单一的、稳定的和不可压缩的流体，流体流动遵从Darcy定律；③忽略自然对流、扩散和辐射换热的影响；④拉应力为正。

图1 内含圆孔的多孔介质无限大平面示意图Figure 1 Schematic diagram of porous medium infinite plane containing circular hole

1.1 控制方程

基于孔祥言[14]《高等渗流力学》第3版(第1，7，12章)，李培超等[7]422饱和多孔介质流固耦合渗流的数学模型，陈丽等[21]752化学-热-弹性模型和本课题组里岳飞龙饱和多孔介质单相热流固完全耦合模型，建立基于LTNE理论的THMC完全耦合的控制方程组。

为降低模型的复杂程度，加快软件的求解速率，将控制方程组简化为一维轴对称的情形进行求解，即将笛卡尔坐标转换为极坐标形式(自变量x，y和z转换成自变量r)。

因此，关于一维轴对称坐标下的热流固化完全耦合控制方程为：

(1)

(2)

(3)

(4)

(5)

式中：ε为多孔弹性体的应变，p为孔隙流体压力，m为溶质摩尔分数变化量，λ为Lame常数，G为Lame常数，K为体积弹性模量，γ为化力耦合参数，β为体热膨胀系数，α为Biot系数，Ts为固体骨架温度，Tf为孔隙流体温度，h为流固界面换热系数，kTs为固体导热率，kTf为流体导热率。每一个物理场控制方程都含有一个主要因变量。

1.2 初始条件和边界条件

数学模型需要一定的定解条件方可求解，即需建立初始条件和边界条件。

设定各物理场在a≤r<∞区域范围内的初始条件为：

(6)

各物理场的边界条件如下：

(7)

此处假设，ma和Ta分别为圆孔边界r=a处溶质摩尔分数的变化增量和固体与流体的加载温度，ma=1.8×10-2，Ta=50 ℃，H(t)为Heaviside函数。

其中，根据文献[22]第12页的内容，整理推导出相关的耦合系数和参数方程如下：

(8)

2 数值方法

2.1 COMSOL Multiphysics求解

COMSOL内部已具有较为完善的模块，但功能最强大的、运用最灵活的仍是其PDE(偏微分方程)模块[16]242。PDE模块可求解用户自定义所研究问题的复杂控制方程组，根据系统提供的假设方程输入，进行数值模拟。

2.2 参数取值

表1为模型中各物性参数取值，部分参数取自参考文献[16]～[17]和参考文献[21]～[22]。

表1 固体和流体的物性参数

3 结果与讨论

3.1 验证

课题组将热流固化4场耦合退化为热流固化3场耦合，通过与陈丽等[21]758的数据对比，验证本研究数学模型的可行性和数值结果的可靠性，如图2所示。图中数据一致性一定程度上说明本方案的可实施性。

图2 本研究退化模型与参考文献模型对比Figure 2 Comparison of proposed degradation model and reference model

3.2 结果分析

课题组借助COMSOL软件平台得到多物理场耦合数值模拟结果。为更好呈现结果，课题组将因变量和自变量进行无量纲化处理。

(9)

式中：mD为量纲为一的摩尔分数变化量，pD为量纲为一的孔隙压力，εD为量纲为一的应变，θs为量纲为一的固体温度。

图3为化学场随时空变化分布图。溶质摩尔分数变化量分布不明显，课题组截取部分数据放大研究(下文有关溶质摩尔质量分数变化量分布均采取局部放大图进行研究)。由图(b)可明显看出，温度升高会引起溶质微妙变化，故刚开始的边界处，溶质摩尔分数变化量有所波动，但波及范围较小，后随时间递增和溶质扩散，波及范围逐渐扩张。

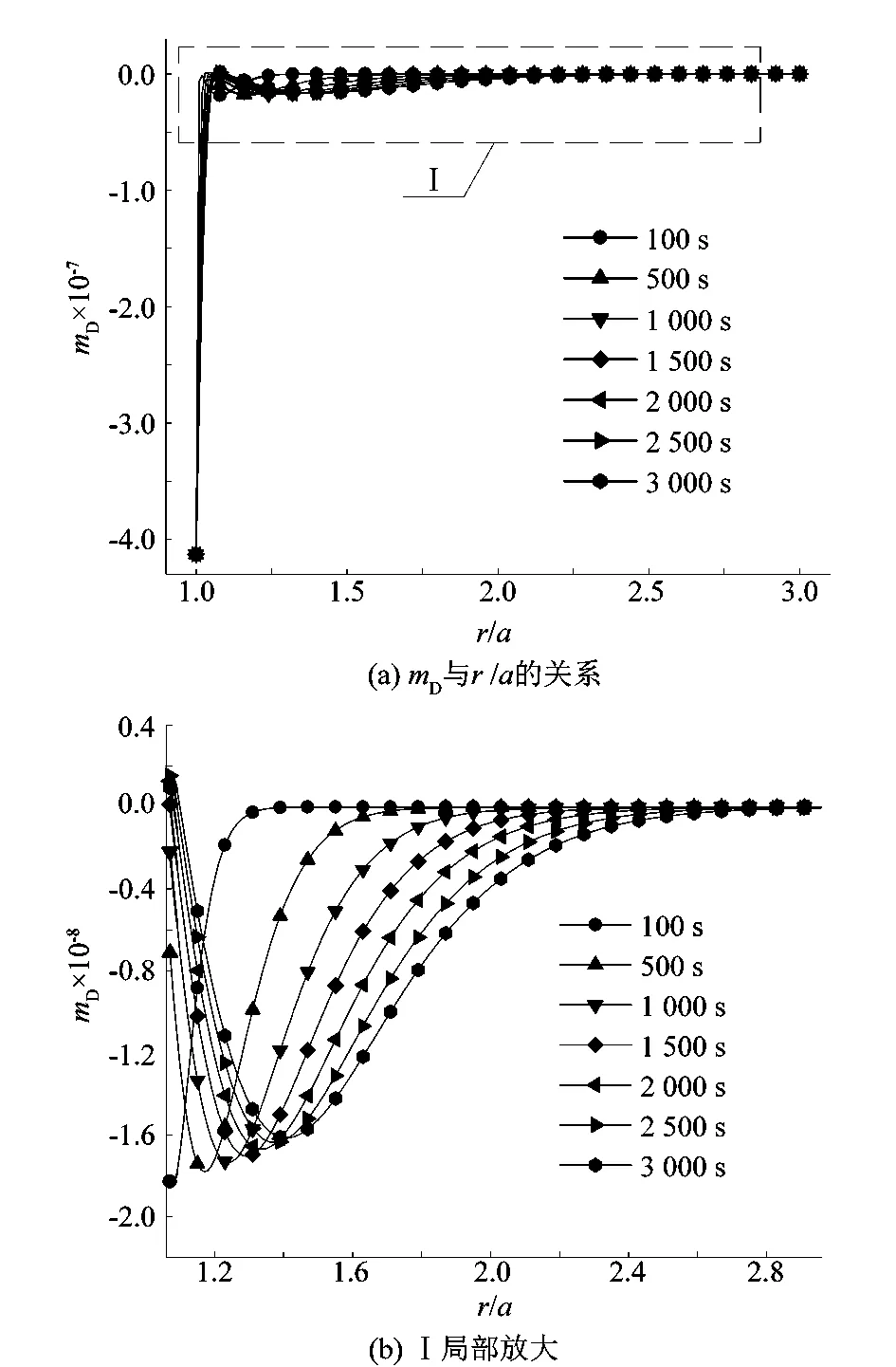
图3 化学场随时空变化分布图Figure 3 Diagram of chemical fields varying over time and space

3.3 参数分析

由于本研究中控制方程中参数较多，故选取有代表性的参数进行研究，分析其对结果影响深浅。课题组选取2 000 s时，研究渗透率k，固体导热率kTs和Biot系数α对多物理场耦合作用。

3.3.1 渗透率的影响

渗透率表征流体在多孔介质中渗透能力的大小。图4展示了不同渗透率对结果的影响，从图中可以看出，孔隙压力随着渗透率的增大先减小后增大。这是由于渗透能力越强，流体流动性越好，孔隙压力能够得到更快地释放，故会出现渗透率越大孔隙压力越小的现象，但到达一定位置后，孔隙压力会回归之前状态。

图4 t=2 000 s时渗透率对孔隙压力影响Figure 4 Influence of permeability on pore pressure at t=2 000 s

3.3.2 固体导热率的影响

导热率是材料最重要的热物性参数之一，描述其导热性能。其对化学场和温度场的影响，如图5所示。由图可知，随固体导热率增加，固体温度增加，温度变化会使得溶质摩尔分数发生细微的变化。

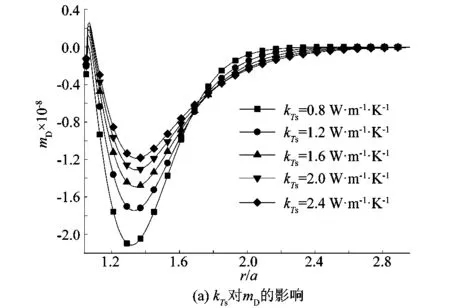
图5 t=2 000 s时固体导热率对mD和θs的影响Figure 5 Influence of heat transfer rate to mD and θs at t=2 000 s

3.3.3 Biot系数的影响

Biot系数又称有效应力系数，描述因孔隙流体支撑载荷而引发骨架刚度变化程度。从图6可看出Biot系数对前几个物理场作用较明显，这是由于骨架刚度变化会引起应力场发生变化，从而引发其他物理场的变化，但应变对温度场贡献较小，Biot系数对温度场影响微乎其微，故此处未展示温度场的分布。

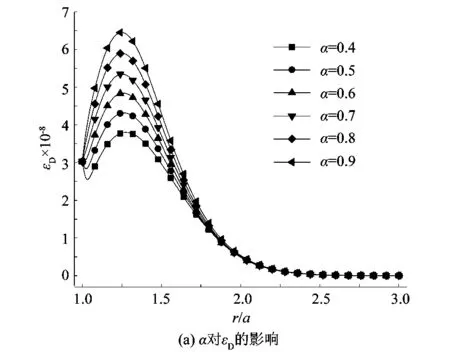
图6 t=2 000 s时Biot系数的影响Figure 6 Influence of Biot coefficient at t=2 000 s

4 结论

课题组基于LTNE理论在多孔介质内发生THMC耦合行为的影响，得出结论如下：

1) 在设定的初边值条件下，随着时间的增加，各物理场相互作用和影响，变化范围逐渐扩大；尤其是化学场，其摩尔分数的影响由深到浅，但最终都将趋于稳定。

2) 各参数对THMC耦合模型影响深远，需选取适当参数进行研究(如对于参数选值，考虑是否会产生较高的热应力，防止结构破坏)；与其他参数比较，导热率对温度的影响较大。

3) 圆孔边界0.1～0.2 m处THMC耦合作用十分明显，说明流体在孔隙中释放的反应速率较快，并周向传播；且在此处，温度场对各物理场的贡献较显著，但反之影响较小。