关联问题的深度处理

姜 胜 杨春芳

(江苏省宜兴第一中学，江苏 宜兴 214200)

当两个或两个以上的物体通过绳、杆连接或直接接触叠放在一起，在不同的约束条件下，物体间的速度、加速度和位移之间存在一定的关联关系，这类问题称之为“关联问题”。解决关联问题的关键在于挖掘隐含的约束条件，不同情境下的“关联模型”之间一般存在着共通的物理规律。

1 连接关联与接触关联的速度关系

物体间的约束关系通常是通过轻绳、轻杆或直接接触产生，大致可分为两类：一类是杆、绳约束物系，其各点速度的关联特征为同一时刻必具有沿杆、绳方向的相同的分速度；二是接触物系，其接触点速度的关联特征为沿接触面法向的分速度必定相同，沿接触面切向的分速度在无相对滑动时相同。绳、杆或者接触面(点)称之为“关联体”，常见“关联模型”如图1、2、3所示。

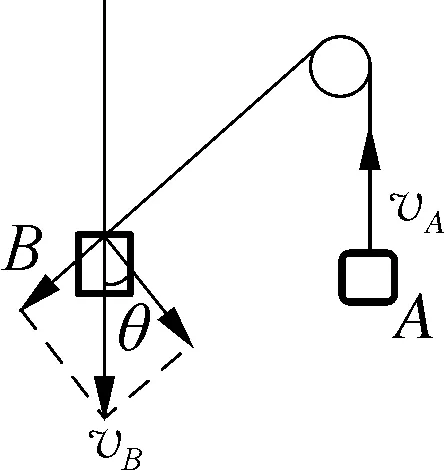
图1

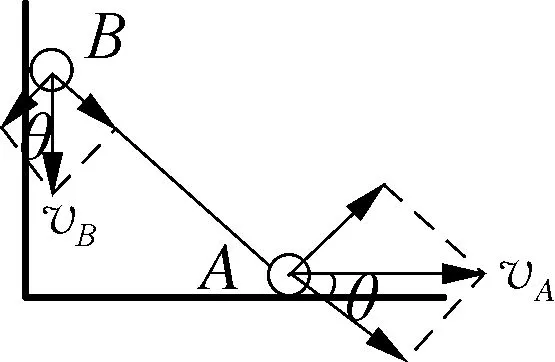
图2

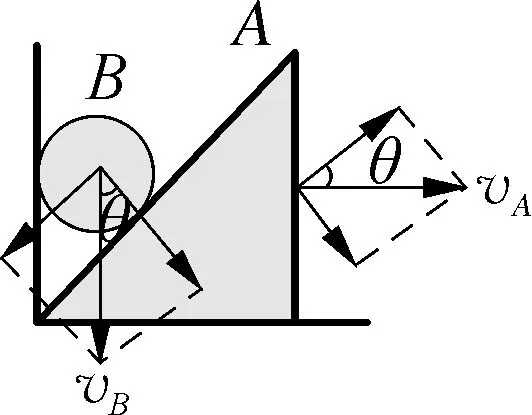
图3

由上述“关联模型”的分析可知：关联速度为沿关联体间弹力方向的分速度，即关联物体间沿关联体弹力方向的分速度相等。所以分解速度时应将物体的速度分解到沿关联体弹力方向和垂直关联体弹力方向，上述情境中的关联速度分别称之为绳端速度、杆端速度与接触速度，以上三幅图中的约束关系分别为：vA=vBsinθ，vAcosθ=vBsinθ，vAsinθ=vBcosθ。

情境1：如图4所示，光滑水平地面上放置质量均为m的两个正三棱柱A、B，其中A固定在地面上，B在外力作用下紧靠着A，A、B中间夹有一个半径为R、质量为2m的光滑圆柱C，整个系统处于静止状态。撤去作用在B上的外力，B与C的速度如何关联呢？

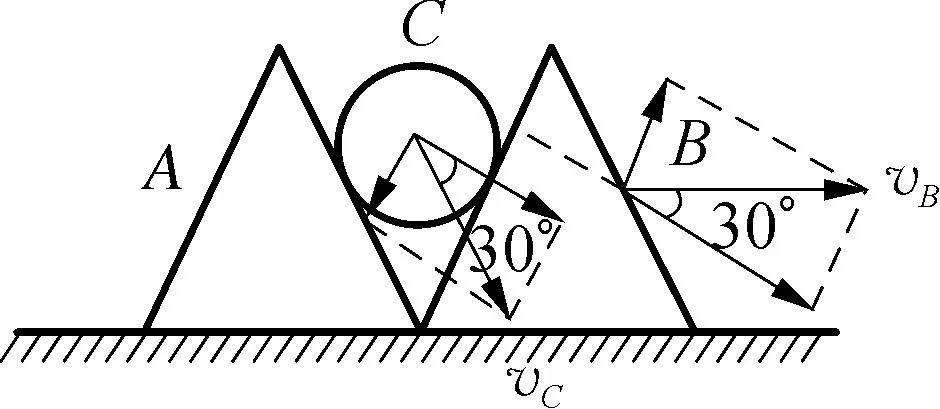
图4

此类问题属于接触关联，C通过B的左侧面与B产生约束关系，由于A固定，C的速度方向与A的右侧面平行，关联速度为B与C的接触速度，即沿接触面法向的分速度。所以将B与C的速度分解到垂直B左侧面和沿B左侧面方向上，如图4所示,约束关系为：vBcos 30°=vAcos 30°，即vB=vC。

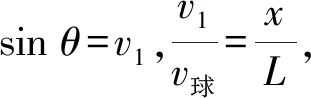
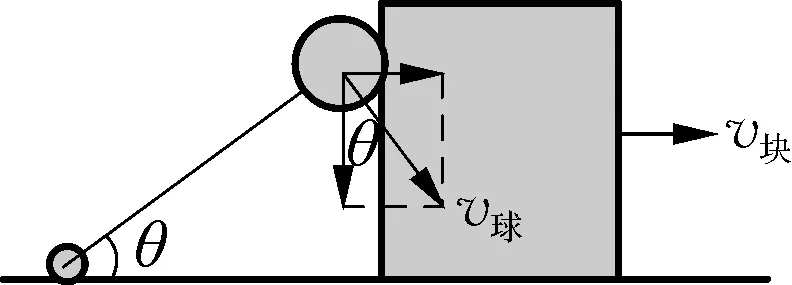
图5

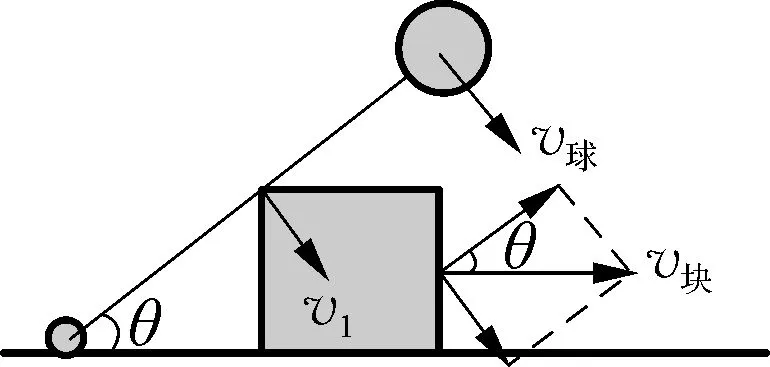
图6

2 “一绳多物”关联模型的速度关系

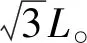
思考1：若将A换做一轻质定滑轮，在其左侧悬挂与甲等质量的物体丙，则挂钩向下运动经过O点时，甲、乙、丙三者的速度关系如何？

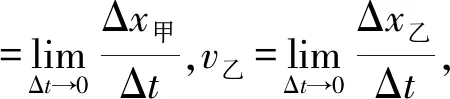
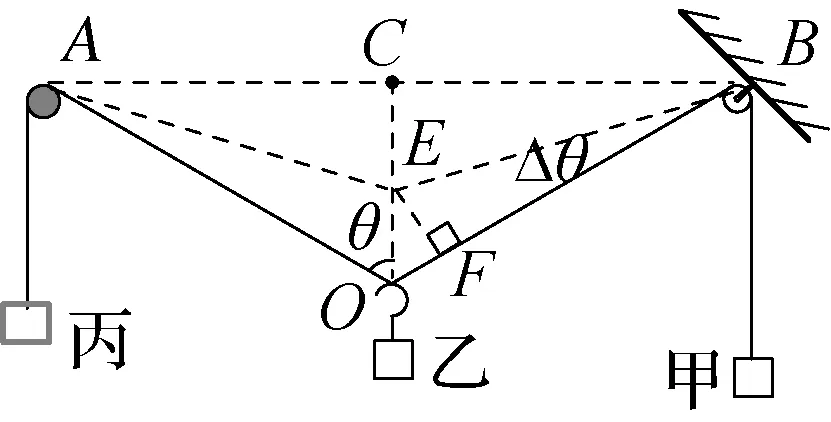
图8

思考2：此物体系属于连接关联，关联体为轻绳，关联速度为沿关联体弹力方向即沿绳方向的分速度，如图9可知其约束关系为：v甲=v丙=v乙cosθ。

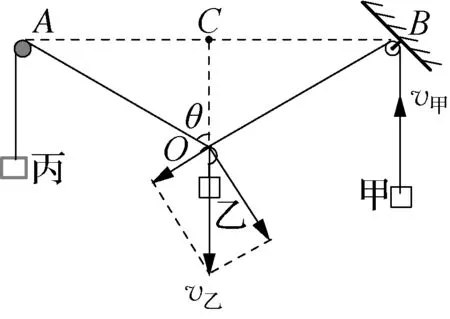
图9

思考3：如图7所示，若A端固定，AO与BO的伸长都会引起甲物体的上升，则约束关系为：v甲=2v乙cosθ。

3 关联速度与关联加速度

绳约束物系中两个物体的速度相关联，但加速度关系与速度关系并不一致，即关联速度的延伸方向上两物体的加速度是不一样的。其原因在于加速度的定义是速度对时间求导，下面从数学的角度讨论绳约束物系中两物体间的加速度关系。

情境3：如图10所示，将质量为2m的重物B悬挂在轻绳的一端，轻绳的另一端系一质量为m的小环A，小环套在竖直固定的光滑直杆上，光滑定滑轮与直杆的距离为d。现将小环从与定滑轮等高的A处静止释放，小环A下滑过程中，小环A与重物B的速度与加速度的约束关系如何？

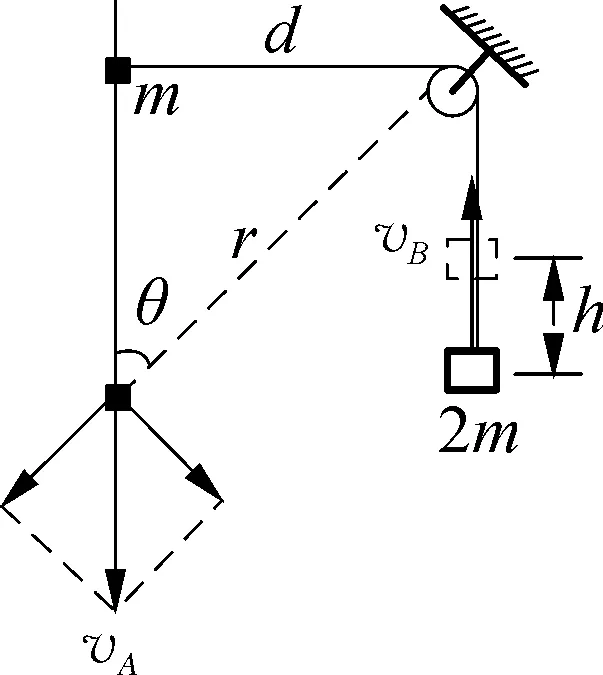
图10

4 关联问题解决策略

关联问题繁杂多样，模型千变万化，然而大道至简，只要弄清了关联速度与关联加速度的数学原理和物理本质，一切问题也就迎刃而解。对于速度关联，首先弄清楚约束关系的类别，分清楚连接关联与接触关联。其次是依据具体物理情境，找准关联体，沿关联体弹力方向的分速度即为关联速度。对于加速度的关系，不能轻率地将速度关系推而广之，应从加速度的定义出发，应用数学方法，寻找约束物体间的加速度关系，对特殊状态下关联加速度进行分析、推理与计算。

对关联问题的深入分析可以帮助我们选择合适的教学策略，以满足不同层次学生的个性化学习需求,并且在必要时进行拓展,满足部分学生深度学习的需求。