基于项目学习培养学生的高阶思维能力①——以“垒出最大长度和面积”为例

王 峰 张国泉

(南京师范大学附属中学，江苏 南京 210003)

现代社会对人才素养的要求偏重于创新、决策、批判性思维、团队协作、获取隐性知识等能力，这些能力被称之为高阶能力，高阶能力的获得是以高阶思维的培养为前提的。布卢姆(Bloom)等专家按照认知的复杂程度，提出六个思维层次，由低到高为：识记、理解、应用、分析、评价、创造，其中分析、评价和创造通常被称为高阶思维。

培养学生的高阶思维能力需要适宜的平台和途径，笔者通过多年的教学实践，发现通过项目学习的方式，促进学生进行系统思考、创新和批判性思维等，可以有效培养学生的高阶思维能力。

笔者受到儿童积木玩具等的启发，设计了“垒出最大长度和面积”的项目学习案例，通过回顾物体重心、杠杆平衡等知识，运用逆向思维、数学递推等方法，进行现场操作、调试和测量，实现垒出的木块组合伸出长度最大和扑克牌组合的面积最大。在实践过程中尝试培养学生高阶思维能力，取得初步成果。

1 运用项目学习，助推高阶思维培养

项目学习有三大特点：(1) 所有项目都是真实的；(2) 每个项目都是独立的，都由确立、实施、归纳总结和结果评估等阶段构成；(3) 项目实施活动所给予学生的不仅是将来做事所需要的知识和能力，还可能是学生将来要做的事情本身。对照上述三点：(1) “垒出最大长度和面积”项目是真实的；(2) 该项目包括确立课题、计划分工、实验操作、反馈调整、结果评估等阶段；(3) 该项目与将来的建筑领域具有相关性，如桥梁建造时工程车利用杠杆原理跨越桥墩(图1)、高层楼房筑墙时用空心砖等，它可以为某些学生将来的工作打下基础，因此该项目非常适合进行“项目学习”。

图1

高阶思维能力主要包含分析、综合、创造等，“垒出最大长度和面积”项目开展过程中需要学生从理论上进行分析，在实践中进行技术运用，在共同研讨、克服困难的过程中发挥集体的智慧，获得灵感并创造性地解决问题，经历这些学习过程后学生的高阶思维能力必定会得到有效提升。

2 分析问题，构建数理模型

2.1 提出问题

将4块相同的木板按照每层一块的要求叠放，则最上面的板相比最下面的板能伸出的最大长度为多大？

2.2 思维建模

正常情况下学生都会从下到上依次垒高木板，在垒的过程中发现：如果第二块板伸出最远的话，那么第三块板就无法伸出更远了。于是需要将第二块板缩进一些，然后将第三块板尽量伸出，再放第四块板时类似的问题又出现了……实验陷入困境。此时教师提醒学生：这种方法是否有缺陷？是否可以换一种思路？引导学生用逆向思维进行处理，即先放最上面的两块，再在下方垫木板，这样会更容易获得最大伸出长度。

2.3 实际操作

先将最上面一块板放在第二块上，形成临界情况后，再将两块板一起放到第三块板上，形成临界情况，以此类推(图2)。

图2

某组学生尝试了多种方法，叠放四块木板的最大长度如表1所示。

表1

2.4 对第4种方法进行数学递推

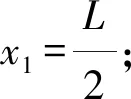
图3

通过充分交流、研讨和点拨，引导学生了解模型构建流程，感受了逆向思维的妙处，突破数学递推的难点，最终学生充分体验到了解决问题的快乐。

3 运用综合方法，分层解决问题

层次1：2块无孔板+2块单孔板；层次2：2块无孔板+2块单孔板+2块双孔板(图4)。均要求每层只放一块板，并使最上面的板相比最下面的板伸出最大长度。

图4

3.1 层次1

通过对板进行挖孔处理，改变板的质量以及重心，让学生将已有经验迁移到新问题情境中去，引发他们进行深度、拓展思考。某组学生尝试了多种方法，叠放四块板伸出的最大长度如表2所示。

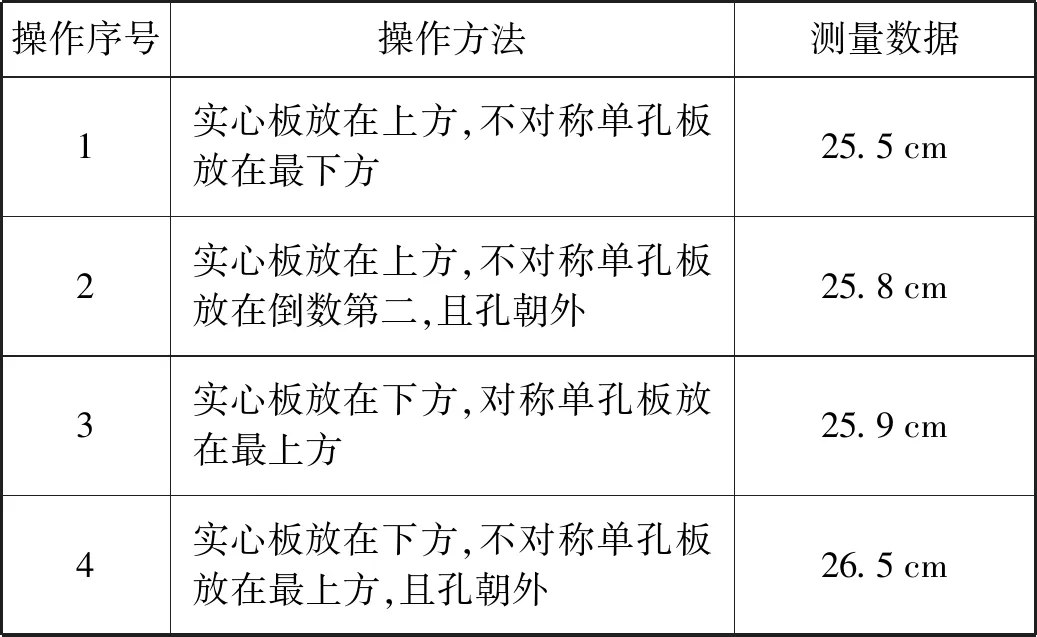
表2

按第4种方法叠放板的效果如图5所示，可得到以下实验结论：(1) 单孔木板放在上方时，可以获得更大的伸出长度，即轻的木板在上方效果更好；(2) 不对称单孔木板在上方，且孔放在外面可以获得更大的伸出长度，即木板轻的部分朝外面效果更好。

图5

3.2 层次2

学生根据上述实验获得的经验，把双孔板放在最上面(不对称的板在上，且双孔朝外)，把单孔板放在中间(不对称的板在上，单孔朝外)，把实心板放在最下面，这时可以获得最大伸出长度(图6)。

图6

通过难度递增的情境设置，引导学生“思维爬坡”，将旧方法不断应用到新问题情境中去，同时又通过不断交流和实践，克服障碍，推陈出新，提升思维能力。

4 自评互评，提升评价水平

通过小组间的相互评价，引导学生学会科学合理地评价他人的活动和成果，了解自己和他人的优势与不足，相互学习和启发，共同进步。

先请“成绩”最好的A组展示成果，分享他们的研究经验并进行自我评价。学生说：其实他们取得的成果也是受到了旁边小组思路的启发，所以他们觉得成绩不仅仅属于自己。

然后再请其他小组的学生对A组的成果进行评价，有的小组说自己也用相同的方法但动作不如A组同学轻柔，所以没有成功；有的小组说自己思路与A组同学的不同，摆放顺序不如A组的合理，成绩不理想；还有的小组说自己小组动作不如A组快，所以还没做完……

通过各个小组的相互评价学习，肯定他人，剖析自我，学生学到了成功的经验，也总结了失败的教训，还逐步学会客观合理地评价自我和他人。

5 开放情境，激发创新能力

开放情境设计1:4块无孔板+2块单孔板+2块双孔板+2块三孔板(图7)。

图7

如果木板的放置方式不设限制，所有板都可以使用，但必须把所有其他板垒在一块板之上，那么相对于最下面的板.上面的板能伸出的最大长度为多少？

通过开放情况设计，解除对学生思维和操作的限制，引导学生运用之前掌握的方法，进行思维再加工，尝试新方法，边总结，边实践，充分调动学生的积极性，激发他们的创造力。

虽然有的小组还是按照之前方法进行叠加(图8)，取得了不错的成绩，但更多的同学愿意进行创新尝试，伸出的最大长度值也一直被不同小组打破刷新(图9)，小组间的相互学习与竞争氛围特别浓厚，研究热情空前高涨，高阶思维能力也在潜移默化中得到提升。

图8

图9

开放情景设计2：多方向二维问题。将一副扑克牌放在一个小平台上，要求只能水平叠放，那么如何叠放才能获得最大的摆放面积呢？

将原来只要求在“单方向上伸展”的一维问题拓展到“多方向上伸展”的二维平面问题，进一步增加思维和操作的难度，学生发现原来的方法有用但有不足之处，需要再寻找新的方法，比如向某方向伸展扑克牌可以仿照板块模式，但不同方向的扑克牌连成片时情况就不同了，需要考虑相互间有覆盖和挤压的情况。

虽然问题比较难，但受到之前获得的“成绩”鼓舞，学生热情高涨投入到新的挑战中。在研究的过程中，他们积极研讨，不断尝试，不断创新，最终获得了比较满意的最大面积(图10)。

图10

完成摆放后，学生要继续采用“数格子”的方法进行面积测定，以获得面积的测量数据，这项技能与“油膜法测分子直径”实验中的操作一致，很容易掌握(图11)。

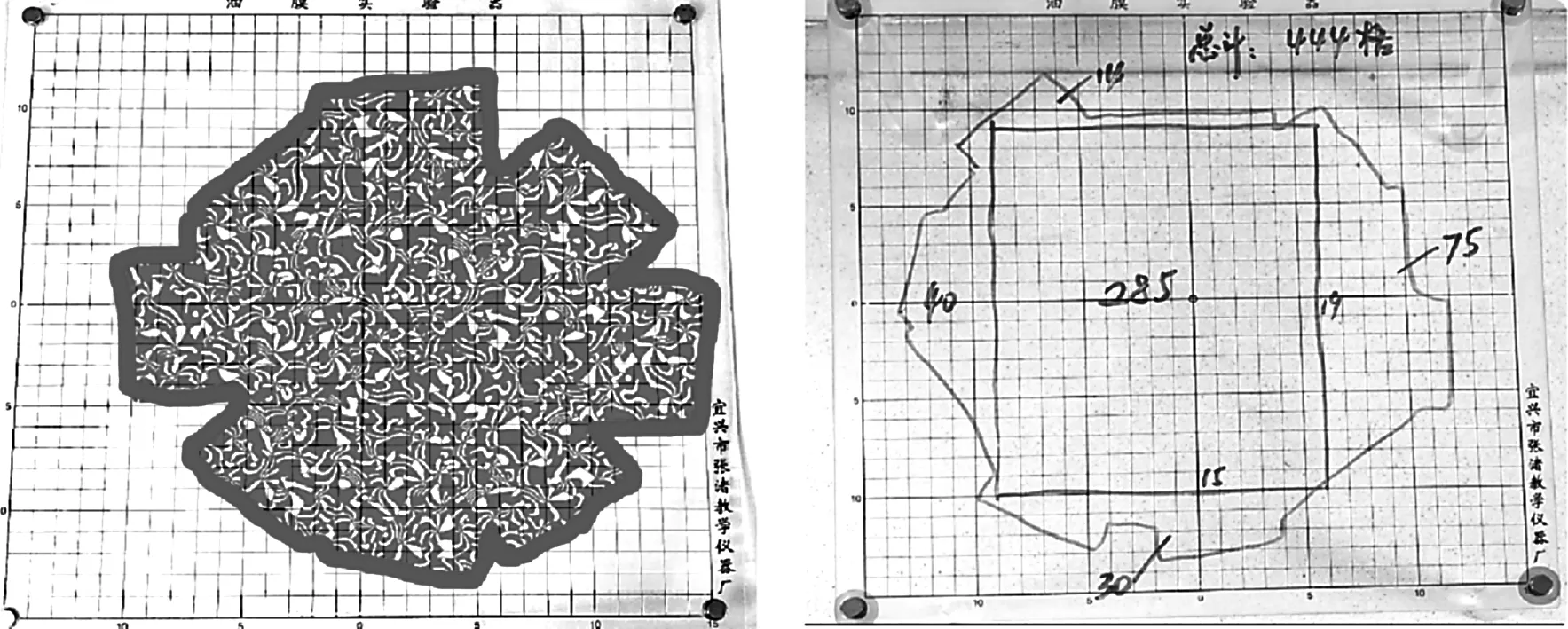
图11

6 归纳总结 反思研究成效

研究活动结束后，笔者对学生进行了一次问卷调查，请他们总结在“垒出最大长度和面积”项目学习过程中的收获，尤其是在高阶思维方面的提升情况，调查结果表明大多数学生认同自己的高阶思维能力能到了有效提升。外请专家也在现场进行了点评，认为这是一节非常好的思维训练课，学生的投入度高，思维活跃，达到了良好的教学效果。学生的收获，专家的认可，给笔者探索培养学生高阶思维能力的途径、方法增加了勇气和信心。

通过“垒出最大长度和面积”项目学习和研究，笔者有不少收获：(1) 一个好的项目的设计是非常重要的，它必须符合项目学习的基本特征，如真实的项目、具有一定的开放度和理论深度、项目能够和将来的学习工作接轨等。(2) 在项目活动推进的过程当中要做好充分准备，利用好各类工具和平台，让学生的思维能够得到最大化的激发，在学生进行理论分析、反馈处理、调整提升、交流合作等过程中，有效地提高他们解决问题的水平，培养他们的高阶思维能力。(3) 在总结反思的过程当中，让他们积极地自评、互评，能够提升学生的评价意识、能力。(4) 在实践的过程中，通过交流互动、头脑风暴等方式，启迪智慧，激发灵感，让学生的创造力得到有效的提升。