指向高阶思维的“萨其曼探究训练”教学模式探讨——以“匀变速直线运动的位移与时间的关系”教学为例

胡 佳 陈志军

(1. 安徽省绩溪县适之中学,安徽 宣城 245300;2. 安徽省绩溪中学,安徽 宣城 245300)

1 问题的提出

《普通高中物理课程标准(2017年版)》指出：物理学科核心素养主要包括“物理观念”“科学思维”“科学探究”“科学态度与责任”四个方面,[1]其中科学思维是核心素养中最重要的组成部分。美国教育家布卢姆将认知过程具体化为记忆、理解、应用、分析、评价、创造六个层次,其中分析、评价、创造为高阶思维,是处于较高认知水平层次上的心智活动或认知能力。[2]在高阶思维的三个认知层次中,分析是基础,评价是核心,创造是目的。[3]

“萨其曼探究训练”教学模式是依据科学家科学研究的实践提出来的,包括展示问题情境、提出假设与收集资料、获得解释、反思探究过程四个环节。[4]在物理教学中运用“萨其曼探究训练”教学模式时，需针对教学任务驱动学习,结合物理概念、物理规律、课堂教学组织、科学思维方法、数学方法、信息技术、探究实验、自制实验器材、联系生活实践等，聚焦问题解决的活动及方法的应用并进行评价,注重知识的生成和批判性思维的运用,是培养学生的高阶思维能力的重要途径。

人教版高中物理教材中“匀变速直线运动的位移与时间的关系”一节，蕴含着丰富的核心素养培育和高阶思维能力培养的素材,有拓展位移公式的应用并进行分析、评价、创造的高阶思维发展点。本文以“匀变速直线运动的位移与时间的关系”教学为例,运用“萨其曼探究训练”教学模式，实施高阶思维导向的物理教学,以提升学生科学探究能力和问题解决能力,达成核心素养的培养目标。

2 指向高阶思维的“萨其曼探究训练”模式应用

2.1 探究匀变速直线运动的位移与时间的关系

本节教材通过对匀变速直线运动v-t图像的分割与累积，探究位移与时间的关系,指明匀变速直线运动v-t图像下的“面积”代表位移,并推导出位移公式，这是本节的教学难点。对于该教学难点,学生的认识仍处于对v-t图像的直观、形象的思维层次,为此，教学实践中可以运用“萨其曼探究训练”教学模式拓展探究，帮助学生理解物理规律,指向高阶思维能力的培养。

探究1:绘制匀变速直线运动的v-t图像，确定初速度和加速度

问题情境：在本章第一节的教学中，我们运用实验方法探究了小车速度随时间的变化规律,选择其中一条纸带(图1),选取纸带上一点为起始点0，后面每5个点取一个计数点,标出0～7共8个计数点,测量出相邻点之间的距离并算出各点对应的速度，填入表1中。

图1

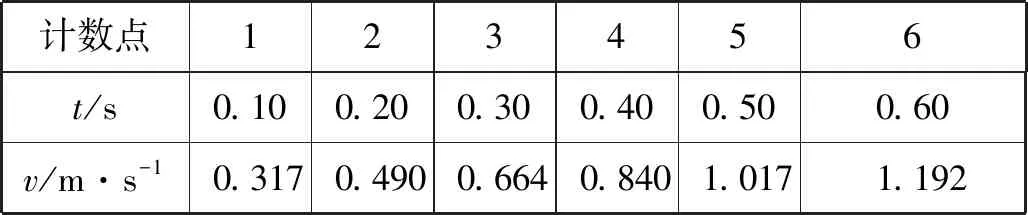
表1

根据表1的测量数据,学生利用专业绘图和数据分析软件Origin Pro进行处理,绘制速度v随时间t变化的散点图,利用线性拟合得到v-t图像(图2),曲线方程为v=0.1398+1.7520t。学生通过拟合并根据所学知识,可以确定小车做匀变速直线运动的加速度a=1.75 m/s2。在计数点的选择上,在教学设计中刻意不展示计数点0左边的相邻点,也就是通过纸带无法利用相邻点之间的平均速度算出计数点0的速度，而是引导学生主动分析、判断,通过拟合确定计数点0的速度,即纸带上所选部分的初速度,根据直线方程容易确定初速度v0=0.140 m/s,借此培养学生的数据处理和问题解决能力。

图2

探究2:绘制匀变速直线运动x-t图像，推得初速度、加速度及位移公式

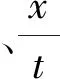
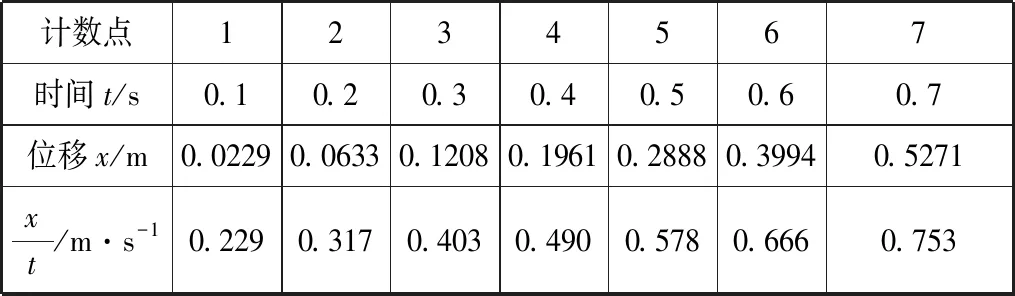
表2

先画出对应的匀变速直线运动位移随时间变化的图像,再引导学生猜想图线是抛物线,由此进入“提出假设与收集资料”阶段,通过分析、辨别、区分、处理数据,推理论证，检验猜想与假设的正确性,发展学生的科学探究和高阶思维能力。

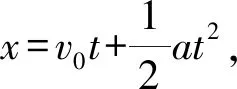
图3

2.2 探究平均速度、中间时刻速度

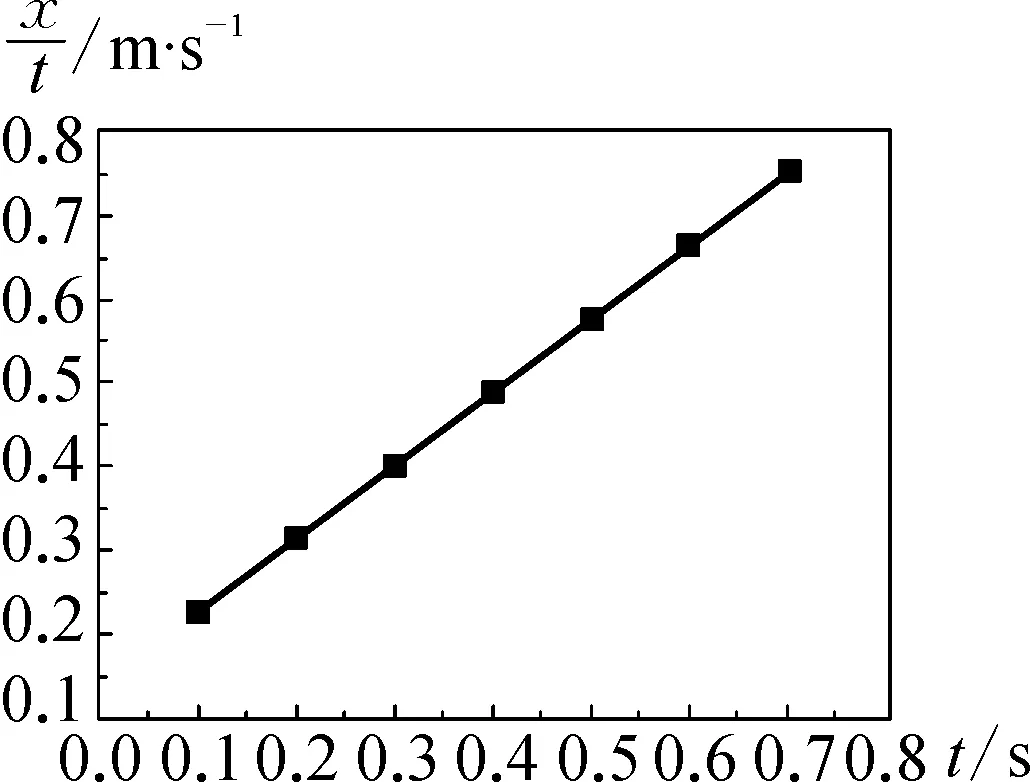
图4

3 结语

在本节课的教学中借助专业函数绘图软件Origin Pro,采用“萨其曼探究训练”教学模式探究匀变速直线运动位移规律,引导学生进行深入探索,使教学指向深度学习和高阶思维能力的培养,达成核心素养的培养目标,培养学生的问题解决能力和创新能力。