关注对数函数、指数函数常见解题误区
刘 洋
(天津市第三十二中学)
学生在求解与对数函数、指数函数有关的问题时,常陷入各种解题误区,以下对常见的解题误区加以归类解析,以期帮助学生全面准确地理解、认识对数函数和指数函数的图像与性质,提高解题效率和解题能力.
1 未注意对数函数的定义域而致错
例1函数的单调递减区间是_________.

剖析错解的根源在于忽视了对数函数y=log3u单调递增,必须满足u∈(0,+∞).
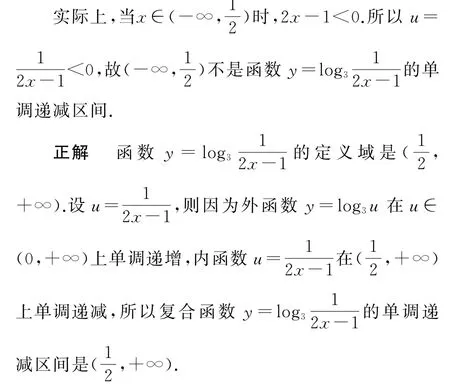
求解与对数函数y=logax(a>0,a≠0)有关的函数的定义域和单调区间时,应优先考虑其本身的约束条件,即x>0.
2 未注意函数图像的渐近线而致错
例2设a>1,则曲线y=|loga(x+1)|与直线x=-3的公共点共有________.
错解如图1所示,在同一平面直角坐标系中分别作出函数y=|loga(x+1)|和x=-3的图像,由图观察即知所求曲线与直线的公共点共有1个.
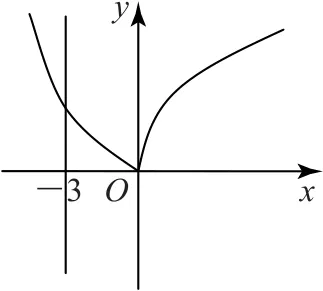
图1
剖析上述错解的根源在于没有注意到对数函数y=logax图像的渐近线——y轴,即直线x=0,从而所作曲线y=|loga(x+1)|的图像不准确,由此致错.
正解如图2 所示,先准确地作出函数y=|loga(x+1)|的图像,注意该函数图像的渐近线为x=-1;然后再作直线x=-3,则由图观察即知所求曲线与直线的公共点共有0个.
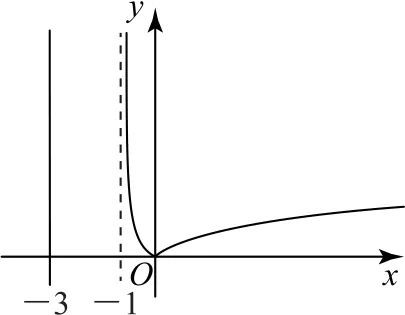
图2
值得注意的是,在利用指数函数、对数函数的图像解题时,准确地作出函数图像是解题的关键所在.
3 未注意函数特性的灵活运用而致错
例3对数函数y=logax与二次函数y=(a-1)x2-x在同一平面直角坐标系内的图像可能是( ).
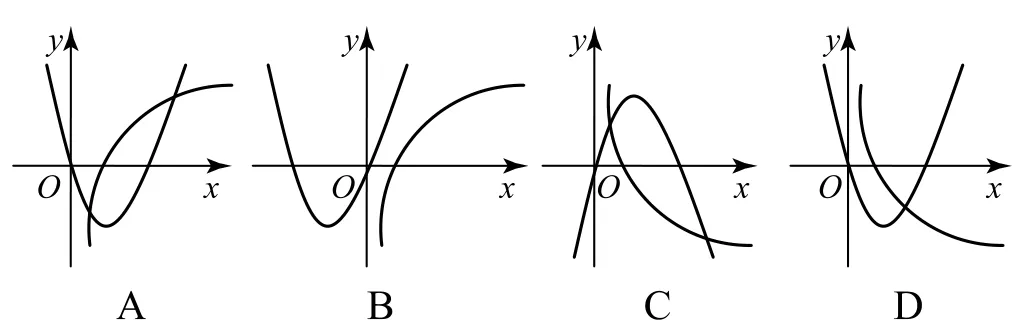
错解如果0<a<1,则因为二次函数图像的开口向下,所以对数函数单调递减,故选C.
剖析错解的根源在于没有注意到当0<a<1时,二次函数与x轴的两个交点满足:一个是坐标原点,一个在x轴负半轴上.故考查二次函数的图像时,不但要注意开口方向,而且要注意函数图像与x轴交点的具体情形.
正解当0<a<1 时,二次函数图像的开口向下,且与x轴的两个交点:一个是坐标原点,一个在x轴负半轴上,所以选项C错误.
当a>1时,二次函数图像的开口向上,且与x轴的两个交点:一个是坐标原点,一个在x轴正半轴上,所以选项B错误,又因为此时对数函数单调递增,所以选项D 也错误.故选A.
遇到二次函数与对数函数在图像方面的交会问题时,要注意认真观察函数的图像,灵活运用函数的特性,加以准确分析.
4 未注意底数对函数单调性的影响而致错
例4如果函数y=a2x+2ax-1(a>0,a≠0)在区间[-1,1]上的最小值为,求a的值.

剖析错解的根源在于分析t的取值范围时,误以为指数函数t=ax在[-1,1]上单调递增.实际上,因为底数a>0,且a≠1,所以指数函数t=ax在[-1,1]上的单调性不确定,故应加以讨论分析.
正解当a>1时,同错解,可得a=3.
当0<a<1时,因为指数函数t=ax在[-1,1]上单调递减,所以,所以当t=a时,由题设知,又0<a<1,解得
综上,a的值为3或.
利用指数函数的单调性解题时,首先要注意底数与1的大小关系,若不确定,则应分情况讨论.一般地,若底数a>1,则有ax>ay⇔x>y;若底数0<a<1,则有ax>ay⇔y>x.
5 未注意对数函数的值域为R 必须满足真数取遍所有的正数而致错
例5若函数f(x)=ln(ax2+2x+1)的值域为R,求实数a的取值范围.
错解依题设,应使ax2+2x+1>0在R 上恒成立,所以解得a>1.
综上,所求实数a∈(1,+∞).
剖析当真数大于零时,并不能保证真数一定取遍所有的正数,从而对应函数的值域也就不一定是R.例如:函数y=lg(x2+1)中的真数x2+1≥1>0,但对应的y≥lg1=0,即函数的值域是[0,+∞),显然就不是R.上述错解,实际上是分析了当函数f(x)的定义域为R时,实数a∈(1,+∞).
正解依题设,应使函数g(x)=ax2+2x+1的函数值取遍所有的正数.
当a=0 时,在原函数f(x)的定义域{x|x>的约束下,函数g(x)的函数值显然可以取遍所有的正数.
当a≠0时,要使二次函数g(x)的函数值取遍所有的正数,则应使解得0<a≤1(注意此时原函数f(x)的定义域可由g(x)>0求得).
综上,实数a的取值范围是[0,1].
求解本题的关键在于,分析题设得到真数ax2+2x+1必须取遍所有的正数.
综上,借误导悟,有利于迅速提高学生对对数函数、指数函数图像和性质的认识与理解,同时也有利于进一步提升学生的直观想象素养、数学运算素养以及逻辑推理素养.
(完)

