目标可观、可测视域下教学问题设计“三立三明”策略初探——以高中数学《必修第一册》“三角函数的概念”(第一课时)为例

吴天然 李志洪

(1.莆田第一中学 2.莆田第二中学)

在基于问题的中学数学课堂教学中,问题质量不高、设计流程不当、教学效果不佳等现象仍时有发生.问题是数学的心脏,是思维的起点.本文根据课题研究总结归纳的初步成果,结合自身教学实践的经验感悟,在课堂教学目标可观、可测的基础上,立足目标、课型、课时,明确问题设计内容维度;立足活动环节评价,明确问题设计难度维度;立足核心素养导向,明确问题设计情境维度,从内容、难度、情境这三个维度,提出“三立三明”的问题设计操作规程及其实施策略,总体规划并统筹协调课堂教学中的问题在内容、难度和情境等方面的理念立意、预期目的和作用效果,辅于高中数学《必修第一册》“三角函数的概念”(第一课时)教学案例并加以评析,教学设计总体框架如表1所示.同时倡导高中数学课堂教学应以问题为载体、以思维为核心,让有效思考贯穿教学的全过程,在提出问题、分析问题、解决问题和再发现问题中学习,把学习知识的过程变成了学生基于问题而自主探究的“再发现”“再创造”的过程,促进数学核心素养落地生根,切实落实立德树人的根本任务,共同营造全方位发展素养、立德树人的有机生态.

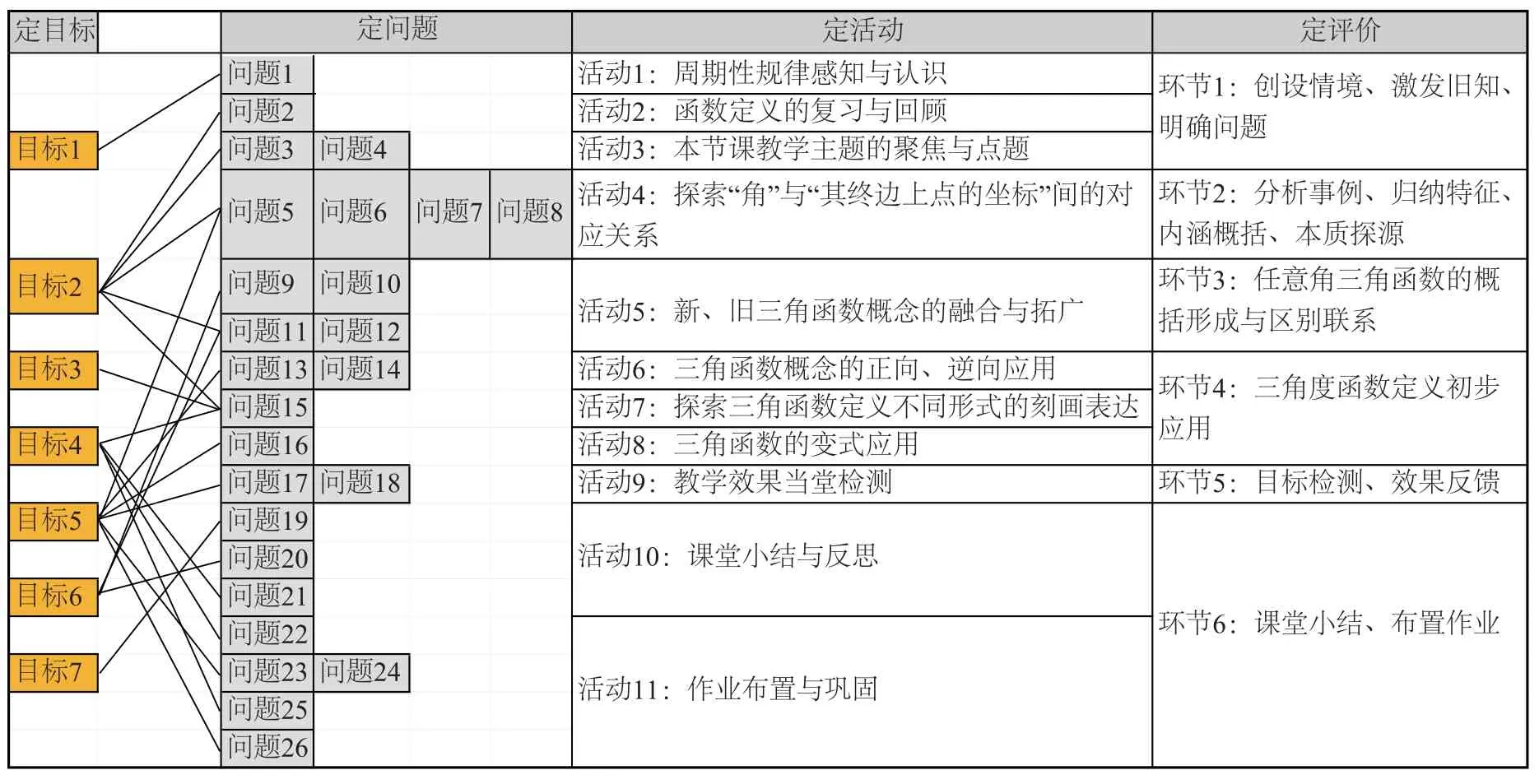
表1 “三角函数的概念”(第一课时)

1 立足目标、课型、课时，明确问题设计内容

按照本课题组研究总结归纳的初步成果,将教学课型划分为概念课型和规则课型.本节课属于概念课型,教学内容侧重于概念原型的举例,概念内涵的抽象概括、刻画描述、辨析分化和理解应用等形成过程,概念外延的列举、分类和判断过程,概念间相互关系的探析和结构体系的建立等内容.

案例1以“三角函数的概念”(第一课时)教学目标设计为例.

根据《普通高中数学课程标准(2017年版2020年修订)》对“三角函数的概念”的教学要求,结合学情分析,设计可观、可测、可评的课堂教学目标,即通过对周期性规律的感知与认识、函数定义的复习与回顾、探索“角”与“其终边上点的坐标”间的对应关系、新、旧三角函数定义的融合与拓广、探索“三角函数定义”不同形式的刻画表达、三角函数定义的正向、逆向、变用等活动,理解三角函数的概念并会初步简单应用,提升抽象概括、运算求解、逻辑推理等数学能力,感悟数形结合、函数方程等数学思想方法,发展数学抽象、逻辑推理、数学运算、数学建模等数学核心素养.评价观测要点如下.

1)能列举出若干具有周期性变化规律的现象,能说出三角函数是刻画现实世界中周期性变化规律的数学工具.

2)通过分析单位圆上点在旋转运动过程中涉及的量及其相互关系,获得对应关系并抽象概括出三角函数的概念,并能对概念的合理性和拓展性进行分析.

3)能复述或写出三角函数概念的内涵,会用符号表示该概念,能用不同的形式或语言进行多元表征并互译.

4)能说出三角函数概念的特征、性质或规律,并正确进行概念辨别或辨析.

5)能正确求出角的终边与单位圆上交点的坐标,会利用三角函数的概念求已知角的三角函数的值,会正确使用角的终边上的任意点坐标求解三角函数,会正确应用三角函数概念解决简单问题.

6)能说出新、旧三角函数概念之间的联系与区别.

7)能说出本节课所涉及的数学思想、方法、能力.

2 立足活动环节评价，明确问题设计难度

《普通高中数学课程标准(2017 年版2020 年修订)》规定了合格水平的学生应知应会的教学内容及其要求层级,是教、学、考、评的标尺.在课堂教学过程中,教师应当根据课标内容标准的有关要求,分析学生的学情,明确学习起始点、目标制高点和评价观测点,以教学环节为评价观测区间,以教学活动为评价观测节点,立足评价逆向进行问题设计.一个环节可以由一个或多个活动有序组合而成,而一个活动同样可以由一个或多个问题有序组织而成,按照最近发展区原则,逐个明确问题设计的难度,合理优化问题难度的梯度,采取目标导向和支架辅助策略,通过问题的逐个解决达成预期目标,达到教、学、评一体化.

案例2以环节3(任意角三角函数的概括形成与区别联系)和活动5(新、旧三角函数概念的融合与拓广)的问题设计为例.

师:(问题9,指向目标6)我们知道“在数学中,引进一个新的概念或法则时,总希望________”.

生:它与已有的概念和法则相容.

师:(问题10,指向目标6)与三角函数有关的“旧”概念有哪些?

生:锐角三角函数的概念——以锐角为自变量,以比值为函数值的函数.

师:(问题11,指向目标2,6)初中所学锐角三角函数的概念是在直角三角形中定义的,如何将原来的定义与今天学习的新知识结合起来呢?

生:将直角三角形放入平面直角坐标系中.

师:很好,那么有哪些步骤呢?

生:第一步,作出Rt△ABC,其中∠A＝α,∠C＝;第二步,以点A为原点,AC为x轴的非负半轴,建立平面直角坐标系,作单位圆,得AB边与单位圆交点P(x1,y1)(假设此时AB＞1);第三步,证明y1＝sinα.

师:锐角三角函数的概念与今天学习的知识是否能够相容呢?

生:可以.

师:(问题12,指向目标2,6)如何将锐角三角函数的概念推广到任意角三角函数的概念呢?

学生回答,教师总结.

活动5基于教学目标可观、可测要点6,用继承和发展的眼光分析锐角三角函数与任意角三角函数的联系,使学生体会两个概念间的和谐统一性,从最近发展区培养学生的逻辑推理核心素养,也为三角函数概念的拓广做铺垫.问题9突出目标导向与思考聚焦,难度偏易;问题10突出切入点探求,难度偏易;问题11突出共性及关联剖析,难度适中;问题12是活动5的目标制高点,难度较大.通过几个小问题从易到难的铺垫引导,通过逐个小问题的解决、评价、反馈与调整,达成探究新、旧三角函数概念间关系的教学目标,从而实现三角函数概念从锐角到任意角拓展的教学目标.

3 立足核心素养导向，明确问题设计情境

基于知识立意导向的情境设计,能巩固旧知但可能导致学生浅层、机械学习.基于能力立意导向的情境设计,有助于学生能力水平的有效提升但可能会导致情智失衡.而只有基于核心素养导向的情境设计,才能真正促进数学学科核心素养落地生根、开花结果,达到关键能力、必备品格和价值观念的有机融合.

案例3以环节4(三角函数定义初步应用)、活动6(三角函数概念的正向、逆向应用)、活动8(三角函数的变式应用)和课后作业的问题设计为例.

例利用三角函数的概念求的正弦、余弦和正切值.

变式1分别求的三个三角函数值.

变式2说出几个使cosα＝1的α的值.

变式3已知点P在半径为1的圆上按逆时针方向做匀速圆周运动,角速度为1rad·s－1,求2s时点P所在的位置.

课后作业选做题:已知点P在半径为2的圆上按顺时针方向做匀速圆周运动,角速度为1.5rad·s－1.求2s时点P所在的位置?

必做题:请以小组为单位,梳理总结三角函数概念的抽象过程,并利用单位圆对三角函数的性质进行猜想.

浅层的学习满足输入,深度学习重于输出.设计问题串设计的目的是促进新知的理解与迁移应用,并完成最后的知识探讨输出.其中例1强调概念的正向应用,进一步理解概念的内涵.例1的变式1强调一些特殊情况(特殊角、特殊位置等)下概念的正向应用,防止出现应用盲区或易错、易混点.例1的变式2强调定义的逆向应用,促进对定义的全面深入理解,检验学生对定义的理解情况.例1的变式3强调定义的综合应用,课后作业中的选做题、必做题,形成一个完整的问题串,充分展示三角函数是刻画匀速圆周运动的数学模型,通过练习使学生从另一个角度理解三角函数的概念,关注知识在生产、生活、实践中的应用,训练了运算求解能力、实践应用意识、数形结合思想,培养了数学建模、逻辑推理、直观想象等数学核心素养.不同立意下的问题情境创设与统筹协调,强化了知识的正向、逆向应用.

(完)