二次求导在解题中的妙用

许国庆

(黑龙江省大庆市第二十三中学)

导数及其应用是高中数学的一个重要的主干内容,也是历年高考中的必考基本知识.利用导数及其应用解决一些相关的函数问题,当一次导函数无法直接(或很难)判断正负取值情况时,可以通过构建新函数,利用二次导函数的正负取值情况分析与解决,这是解题常用的方法.本文结合实例加以剖析,以期指导复习备考.

1 利用二次求导判断函数的单调性

例1已知函数,试求函数f(x)的单调区间.

分析根据题目条件,先确定函数f(x)的定义域,通过对函数f(x)求导,从导函数的分式结构出发进一步构建函数,通过二次求导来确定一次导函数的单调性与最值,从而得以确定函数f(x)的单调区间.

解由于函数f(x)的定义域为x∈(0,1)∪(1,＋∞),求导得,令函数u(x)＝,所以u(x)在(0,1)上单调递增,在(1,＋∞)上单调递减,故当x∈(0,1)∪(1,＋∞)时,u(x)＜u(1)＝0,即f′(x)＜0,因此函数f(x)在(0,1)和(1,＋∞)上单调递减.

在利用导数判断函数的单调性时,特别是导函数中的部分关系式(分式中的分子或分母中的一者易确定正负,另一者不易确定正负等情况)的符号很难直接判断或无法确定时,可以构造新的函数,采用二次求导处理,判断出一次导函数的符号以及最值,进而最终确定函数的单调性.

2 利用二次求导判定代数式的大小

例2若函数,0＜x1＜x2＜1,设a＝f(x1),b＝f(x2),则a,b的大小关系是( ).

分析根据题目条件,关键是确定函数f(x)在(0,1)上的单调性,但直接判断单调性较困难,且求导后难以确定导函数的符号,从而考虑将一次导函数中分子所对应的关系式视为新函数,利用二次求导确定一次导函数的单调性与最值,再确定函数f(x)在(0,1)上的单调性,进而判定代数式的大小关系.

解由于函数,求导得f′(x)＝,令函数g(x)＝xcosx－sinx,x∈(0,1),求导得g′(x)＝－xsinx＜0,所以函数g(x)在(0,1)上单调递减,则g(x)＜g(0)＝0,所以f′(x)＜0,即函数f(x)在(0,1)上单调递减,而0＜x1＜x2＜1,则f(x1)＞f(x2),即a＞b,故选A.

利用导数判定代数式的大小,其实质就是判断函数的单调性.对于以上问题,为得到函数f(x)在(0,1)上的单调性,需判定一次导函数f′(x)的符号,而其分母为正,那么只需判断分子xcosxsinx在给定区间上的符号,由于很难直接判断,故通过二次求导,判断出一次导函数的符号,最终得以顺利解决问题.

3 利用二次求导确定参数的最值(或取值范围)

例3已知函数f(x)＝2(x－2)ex＋a(x2＋4x)＋4,其中a∈R,e为自然对数的底数.若不等式f(x)≥0在区间[0,＋∞)上恒成立,求实数a的取值范围.

分析根据题目条件,求出函数f(x)的导数,通过对参数分a≤0与a＞0讨论,当a≤0时直接确定不等式不可能恒成立;而当a＞0时,结合二次求导处理,进一步对参数分4a－2≥0与4a－2＜0讨论,确定不等式是否恒成立,从而得以确定参数的取值范围.

解对f(x)求导可得

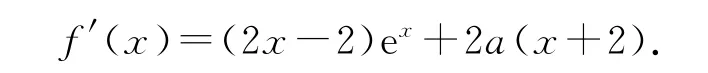
当a≤0 时,若x∈(0,1),则f′(x)＜0,所以f(x)在(0,1)上单调递减,又f(0)＝0,所以f(x)＜0,故f(x)≥0在[0,＋∞)上不可能恒成立.

当a＞0 时,令g(x)＝f′(x)＝(2x－2)ex＋2a(x＋2)(x≥0),则g′(x)＝2xex＋2a,则g′(x)＞0,所以y＝g(x)在[0,＋∞)上单调递增,则f′(x)≥f′(0)＝4a－2.

当4a－2≥0,即时,y＝f(x)在[0,＋∞)上单调递增,所以fmin(x)＝f(0)＝0,故f(x)≥0在[0,＋∞)上恒成立.

当4a－2＜0,即时,f′(0)＝4a－2＜0,f′(1)＝6a＞0,故存在x0∈(0,1)使得f′(x)＝0,此时函数y＝f(x)在(0,x0)上单调递减,又f(0)＝0,所以f(x)在(0,x0)上恒小于0,故f(x)≥0在[0,＋∞)上不可能恒成立,故不符合题意.

综上,实数a的取值范围

在利用导数求解参数的最值(或取值范围)时,求解的关键是确定导函数的零点,如果能够直接确定该方程的解就相对简单一些,若求解导函数的零点有困难或无法求解时,可以考虑构建新函数,借助二次求导转化与变形.

4 利用二次求导证明不等式

例4已知函数f(x)＝ex－x－x2,x∈(0,＋∞).求证

分析根据题目条件,通过对函数f(x)求导,此时无法确定一次导函数f′(x)的零点,进一步构建函数进行二次求导,求出二次导函数的零点并确定其符号,从而确定一次导函数的单调性,最后结合函数的极值确定一次导函数的零点,从而确定函数f(x)的单调性与最值,综合二次函数的图像与性质证明即可.

解对函数f(x)求导得f′(x)＝ex－2x－1,构造函数g(x)＝ex－2x－1,求导得g′(x)＝ex－2,令g′(x)＝0,解得x＝ln2.

当x∈(0,ln2)时,g′(x)＜0,当x∈(ln2,＋∞)时,g′(x)＞0,所以函数f′(x)在区间(0,ln2)上单调递减,在区间(ln2,＋∞)上单调递增,则

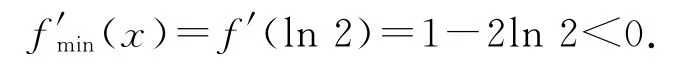
在(0,ln2)上,f′(x)＜f′(0)＝0,而在(ln2,＋∞)上,f′(1)＝e－3＜0,,所以存在)使得f′(x0)＝0,即ex0－2x0－1＝0,所以函数f(x)在(0,x0)上单调递减,在(x0,＋∞)上单调递增,所以

结合二次函数的图像与性质,可知fmin(x)＞

在利用导数证明不等式时,证明的关键在于构造适当的函数,在一次求导后无法明确或直接求出导函数的零点时,可以通过在相应区间上用二次求导的方法判定一次导函数的符号,进而得到一次导函数的单调性,最后再利用原函数的单调性来证明相应的不等式.

在解决一些函数问题时,函数的图像与性质虽然可以直观地反映出两个变量之间的变化规律,但大多数复合函数或复杂的函数作图困难较大,这时可以借助导数及其应用,特别是进行二次求导,拓展应用函数的图像与性质解题的空间,让导数这个强有力的工具为函数的单调性、极值、最值等相关问题的研究提供更为简单、程序化的方法,具有更强的可操作性、可应用性.

链接练习

1.(2022年全国乙卷理16)已知x＝x1和x＝x2分别是函数f(x)＝2ax－ex2(a＞0 且a≠1)的极小值点和极大值点.若x1＜x2,则a的取值范围是________.

2.若过点P(1,λ)最多可作出n(n∈N*)条直线与函数f(x)＝(x－1)ex的图像相切,则下列结论中错误的是( ).

A.λ＋n＜3

B.当n＝2时,λ的值不唯一

C.λn可能等于－4

D.当n＝1时,λ的取值范围是

链接练习参考答案

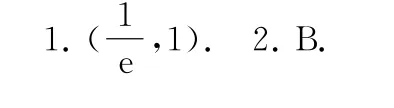
(完)