构造函数利用单调性比较大小例析

李 晶 张国坤

(云南省曲靖市第一中学)

比较大小问题,每年高考几乎必考.比较两个“复杂”数的大小,方法较多,构造函数并利用函数的单调性比较大小是一种常用的路径,这种路径在求解高考试题的比较大小问题中经常发挥有效的作用.构造函数比较a,b两个数的大小,典型的有三种方法.

1 构造函数比较大小的三种典型方法

1.1 单调比较法

若研究发现a,b存在相同的结构特点,或者通过变形处理,能将a,b配凑出相同的结构特点,则可根据两个数共同的结构特点,从特殊到一般,构造函数f(x),使得a＝f(x1),b＝f(x2),选择区间D,说明x1,x2∈D且x1＜x2,只要证明f(x)在区间D上单调,即可比较f(x1)与f(x2)即a与b的大小.

1.2 作差比较法

要比较a,b的大小,只需比较a－b与0的大小,则根据a－b的结构特点,构造函数f(x),使得存在x0,t0有f(x0)＝0,f(t0)＝a－b,只要说明或证明函数f(x)在区间[x0,t0]或[t0,x0]上的单调性,即可比较a－b与0的大小关系,进而比较a,b的大小.

1.3 作商比较法

要比较两个正数a,b的大小,只需比较与1的大小,则根据的结构特点,构造函数f(x),使得存在x0,使,只要说明或证明函数f(x)在区间[x0,t0]或[t0,x0]上的单调性,即可比较与1的大小,进而知道a,b的大小关系.

2 三种典型方法的应用举例

例1(2022年全国甲卷文12)已知9m＝10,a＝10m－11,b＝8m－9,则( ).

解析9m＝10的本质就是给出m的值,即m＝log910.a＝10m－11与b＝8m－9之间有什么联系呢?

a＝10m－10－1,b＝8m－8－1,两个式子的结构特点是一致的(称作同构).构造函数f(x)＝xm－x－1,则f(9)＝9m－9－1＝0,f′(x)＝mxm－1－1.

m＝log910＞1,当x＞1 时,xm－1＞x0＝1,则f′(x)＞m－1＞0,函数f(x)在(1,＋∞)上单调递增,进而f(10)＞f(9)＞f(8),即a＞0＞b,故选A.

例4(2021年全国乙卷理12)设a＝2ln1.01,b＝ln1.02,,则( ).

例5(2021年八省联考卷8)已知a＜5且5ea＝ae5,b＜4且4eb＝be4,c＜3且3ec＝ce3,则( ).

解析将关于a,b,c的条件等价转化:

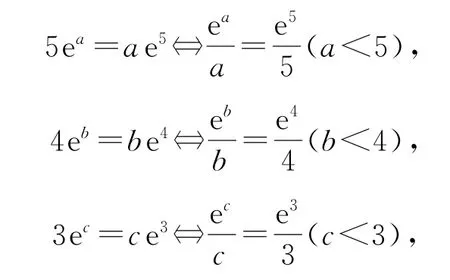
根据三个等式的结构特点(同构),构造函数f(x)＝,f′(1)＝0,f(x)在(0,1)上单调递减,在(1,＋∞)上单调递增,且知0＜a＜1,0＜b＜1,0＜c＜1,f(5)＞f(4)＞f(3),所以f(a)＞f(b)＞f(c),0＜a＜b＜c＜1,故选D.

例6已知a＝log20212022,b＝log20222023,c＝log20232024,则( ).

A.a＞b＞cB.b＞a＞c

C.b＞c＞aD.c＞a＞b

a,b,c的结构有一个共同特点就是:每个数都是一个幂,幂中的指数恰好等于底数的倒数,a,b,c中的底数逐渐增加1,构造函数f(x)＝当x＞e时,g′(x)＜0,函数g(x)在(e,＋∞)上单调递减,则f(x)在(e,＋∞)上单调递减,f(2021)＞f(2022)＞f(2023),即a＞b＞c,故选D.

例8已知a＝20212022,b＝20222021,c＝2021.52021.5,则( ).

由f(2021)＞f(2021.5),可得a＞c.

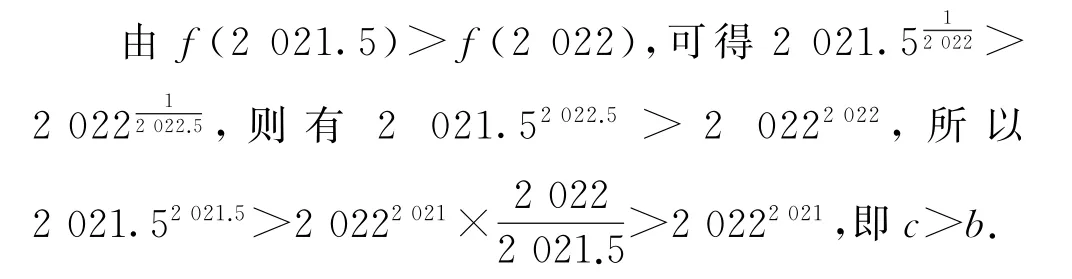
综上,a＞c＞b,故选D.

例9已知f(x)是定义在R 上的可导函数,且f(0)＝1,f(x)＜f′(x),则( ).

综上,故选B.

(完)