导数应用的创新型试题赏析

田长江

(青岛西海岸新区第一高级中学)

创新是引领发展的第一动力,因此培养学生的创新意识非常重要.本文通过梳理总结列举出了导数应用试题中的几类创新型问题,并结合例题进行分析,供读者借鉴赏析.

1 新定义型

例1丹麦数学家琴生(Jensen)是19世纪对数学分析做出卓越贡献的巨人,特别是在函数的凸凹性与不等式方面留下了很多宝贵的成果.

设函数f(x)在(a,b)上的导函数为f′(x),f′(x)在(a,b)上的导函数为f″(x),若在(a,b)上f″(x)＞0恒成立,则称函数f(x)在(a,b)上为“凹函数”.

已知f(x)＝ex－1＋xlnx－tx2在(1,2)上为“凹函数”,则实数t的取值范围是( ).

点评二阶导数与函数凹凸性的关系来自于高等数学内容,对于新定义问题有着“起点高,落点低”的特点,在解决这类问题时,关键在于抓住所给函数的新定义,利用导数研究函数的方法求解参数的取值范围.新定义题型的问题,别致新颖,有利于检测学生的创新能力.

2 开放型

例2写出一个同时满足下列要求的连续函数f(x)＝_________.

①f(x)的表达式中至少含有ex,xn(n∈N*),lnx中的两个;

②存在一个极值点x＝3.

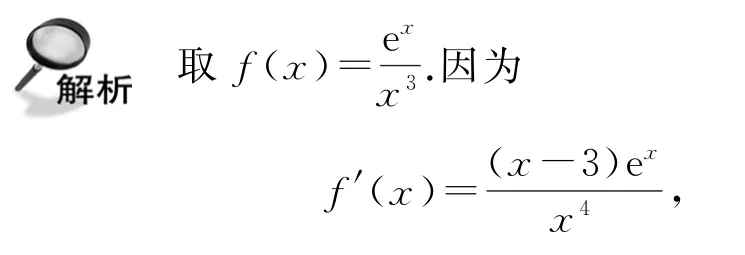
所以当x＞3时,f′(x)＞0,当0＜x＜3或x＜0时,f′(x)＜0,所以f(x)在(－∞,0)(0,3)上单调递减,在(3,＋∞)上单调递增,所以x＝3是f(x)的一个极值点,所以符合题意(答案不唯一).

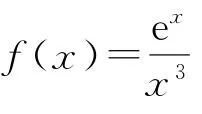
点评求解开放型问题的关键在于弄清楚题目所给的条件,紧抓条件的具体内容构造满足条件的函数.

3 问题研究型

例3函数f(x)＝－x3＋3x2＋9x－2.

(1)求f(x)的极大值和极小值;

(2)已知f(x)在区间D上的最大值为20,以下3个区间D的备选区间中,哪些是符合已知条件的? 哪些不符合? 说明理由.

①[－3,2];②[－2,2];③[－3,1].

解析(1)f′(x)＝－3x2＋6x＋9＝－3(x＋1)·(x－3),令f′(x)＝0,解得x＝－1或3.

当x∈(－∞,－1)时,f′(x)＜0;

当x∈(－1,3)时,f′(x)＞0;

当x∈(3,＋∞)时,f′(x)＜0.

所以f(x)在(－∞,－1)和(3,＋∞)上单调递减,在(－1,3)上单调递增,所以f(x)的极大值为f(x)的极小值为

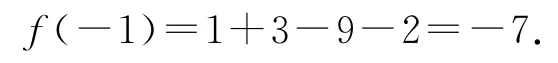
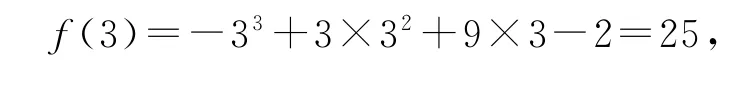
(2)当区间D为①时,f(x)在[－3,－1]上单调递减,在(－1,2]上单调递增,且

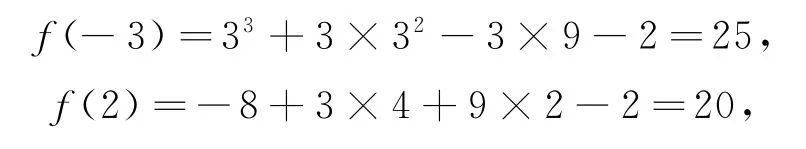
所以fmax(x)＝25,不符合已知条件.

当区间D为②时,f(x)在[－2,－1]上单调递减,在(－1,2]上单调递增,且

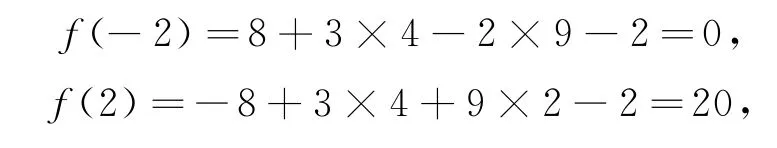
所以fmax(x)＝20,符合已知条件.

当区间为③时,f(x)在[－3,－1]上单调递减,在(－1,1]上单调递增,有

所以fmax(x)＝25,不符合已知条件.

综上,区间①、区间③不符合已知条件,区间②符合已知条件.

点评本题需要研究符合条件的区间,给出三个区间进行选择,使得问题呈现形式新颖独特,能够较好地考查学生的思维能力.本题的求解要根据f(x)在所给区间上的单调性和极值,分析得到f(x)的最大值,由此判断所给区间是否符合条件.

4 知识交会型

例4已知函数,下列对于函数f(x)性质的描述,错误的是( ).

由f′(x)＞0,可得

综上,故选C.

点评以三角函数为背景考查导数知识和基本初等函数的性质,是这类问题的常见命题形式,在解决此类问题时,要能够正确求出所给函数的导数,利用导函数研究函数的基本性质.

(完)