高炉炉缸内衬侵蚀边界研究

马小刚，夏 楠，吴传宗，吴鹏程

（辽宁科技大学 机械工程与自动化学院，辽宁 鞍山 114051）

高炉是一种巨型的炼铁热工设备，位于其中下部的炉缸是安全事故多发的部位。生产过程中，由耐火材料砌筑而成的炉缸内衬直接与高温铁水接触，在铁水冲刷、热应力以及化学侵蚀等因素的综合作用下［1-4］，发生不可逆的侵蚀损伤。炉缸内部环境复杂且多变，内衬多呈不均匀性侵蚀减薄，严重时可引发炉缸烧穿事故。然而炉缸内部处于高温、密闭、铁水淹没等恶劣工作环境，内衬的侵蚀状态无法直接探察，对内衬侵蚀状态和安全风险掌握不准确是造成炉缸烧穿的主要原因［5］。近年来，Zagaria［6］、Brannbacka［7］、吴俐俊［8］、Feng［9］和Su［10］等均以二维传热理论为基础，建立侵蚀数学模型，通过调整模型的侵蚀边界，使数学模型的温度分布与实际一致，实现炉缸内衬侵蚀边界求解。这些方法均具有较高的计算精度，但也存在不足之处：只对求解原理进行介绍，对求解过程的描述过于模糊，很难完全复现；计算原理较复杂，对专业软件熟练度的要求较高，不利于在高炉现场推广使用；计算均以内衬中热电偶的温度数据为依据，由于长时间在高温下工作，一部分热电偶会失效，导致计算精度降低。如何将复杂的理论应用于实际，为高炉现场提供一种便捷可靠的计算工具，以及当热电偶失效后如何科学地监控炉缸安全状态已成为亟需解决的课题。

本文利用数值求解方法，结合预埋在炉缸内衬中热电偶的测温数据，提出一种可同时计算内衬侵蚀边界和铁水凝固边界的移动边界搜索方法。并以AG-3号高炉为例，通过对炉缸内衬侵蚀形貌的持续监测以及炉缸内衬的历史侵蚀过程进行分析［6］，验证移动边界法可行性。并推导出炉缸侧壁内衬安全厚度计算公式。

1 移动边界法的原理及计算

1.1 移动边界法计算原理

构建高炉炉缸部位铁水凝固边界和内衬侵蚀边界计算模型，如图1所示。

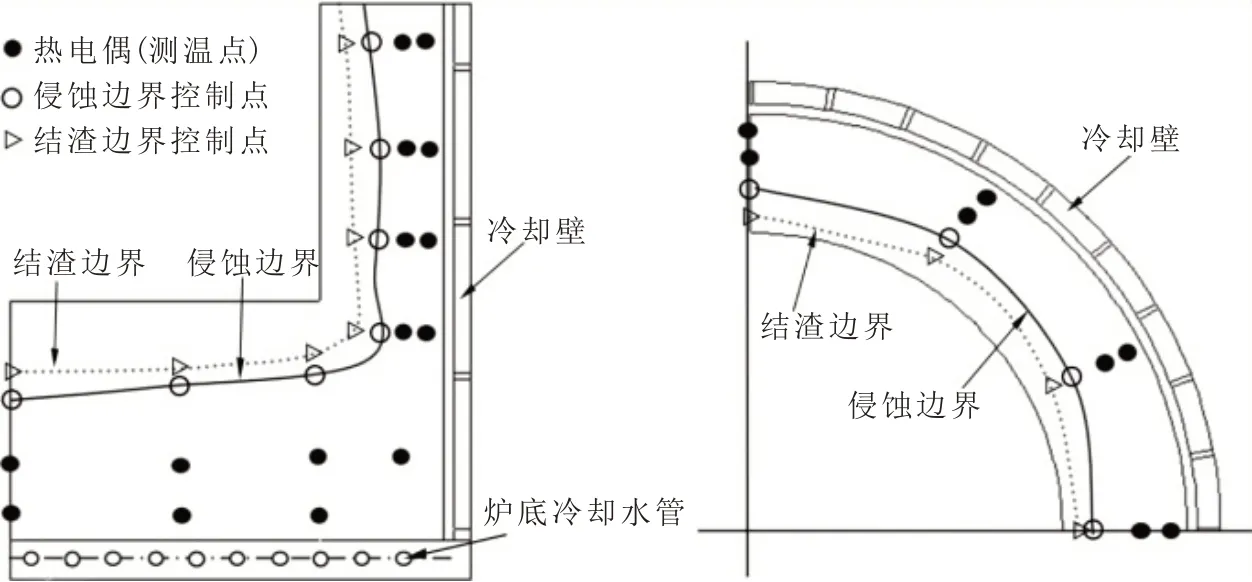
图1 内衬侵蚀边界示意图Fig.1 Schematic diagram of lining erosion boundary

在炉缸内衬中预埋热电偶，实测温度TiT（i=1，2，…，n），n为数据总数。运用数值理论计算得出炉缸中各测量点位置的温度TiC（i=1，2，…，n），n为数据总数。若计算值与实测值一致，则

移动边界法按照理论计算结果移动模型的内衬侵蚀边界和铁水凝固边界，使计算值和实测值相等。设1 150℃等温线位置为铁水凝固边界［11］；热电偶温度最高时对应的铁水凝固边界为内衬的实际侵蚀边界。

计算流程如图2所示。首先要构建具有可移动内衬侵蚀边界和铁水凝固边界的计算模型。在二维计算时，可根据热工测量点的位置设置边界控制点。位于炉底的控制点，限制其只能沿着高度方向移动；位于炉缸侧壁的控制点，限制其只能沿着半径方向移动。

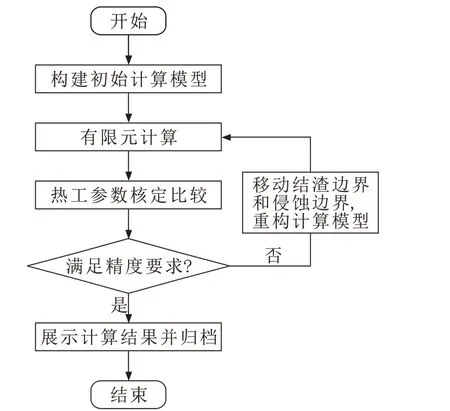
图2 移动边界法求解流程Fig.2 Solving process of moving boundary method

1.2 炉缸内衬初始侵蚀边界计算

以炉缸侧壁为例，采用长圆筒一维传热理论计算侵蚀边界控制点的初始位置［12］，炉缸侧壁的一维传热示意图如图3所示。Qtotal为铁水传入炉缸内衬的总热量，Qwater为冷却壁中冷却水强制对流换热带走的热量，Qair为炉缸周围空气自然对流换热带走的热量，Ta、Tb分别为两热电偶位置的温度，Ts为铁水凝固温度，r1～r4分别为各特征位置的半径，rs为侵蚀位置的半径。初始侵蚀边界可能位于碳砖层或陶瓷杯层。

图3 炉缸侧壁一维传热示意图Fig.3 Schematic diagram of 1-D heat transfer of hearth side wall

1.2.1 炉缸侧壁初始侵蚀边界位于碳砖层 当初始侵蚀边界位于碳砖层时，采用单层长圆筒壁一维传热理论［13］，利用位于r3、r4位置的两个热电偶测得的温度值Ta、Tb计算。

碳砖的导热系数为

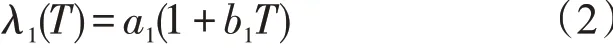
式中：a1和b1为常数；T为温度，℃。

两个热电偶之间的单位热流量为rs与r3之间的单位热流量为

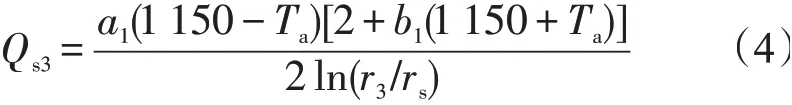
对于稳态导热，有

解得

1.2.2 炉缸侧壁初始侵蚀边界位于陶瓷杯层

当炉缸侧壁初始侵蚀边界位于陶瓷杯层时，采用多层圆筒壁一维传热理论［14］，利用位于r3、r4的两个热电偶的读数Ta、Tb，以及炉缸各部位的尺寸参数，计算侵蚀边界位置rs。

碳砖中温度分布

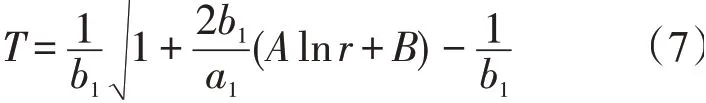
式中：A和B为两待定系数；r为半径。

两热电偶所在位置的温度分别为

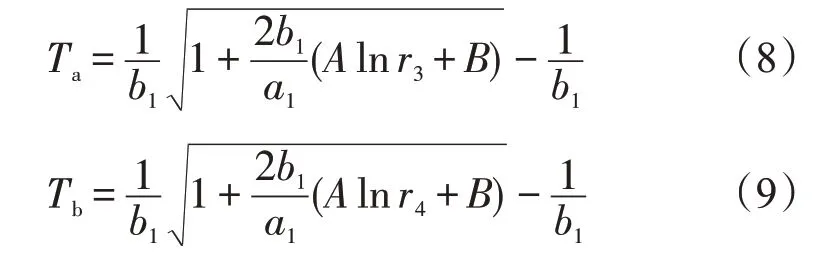
联立式（8）和式（9），可解得

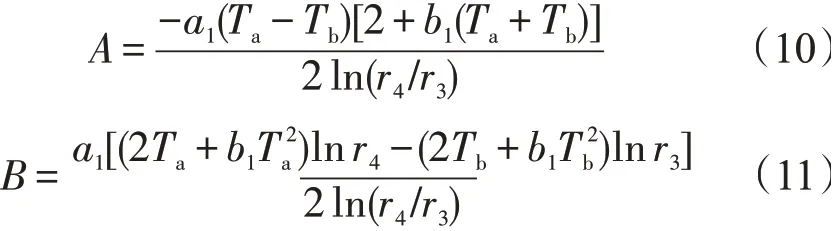
碳砖和陶瓷杯交界位置r2处的温度为

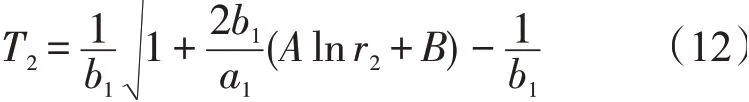
陶瓷杯的导热系数为

则碳砖和陶瓷杯交界位置r2和侵蚀位置rs之间的单位热流量为

对于稳态导热，有

解得

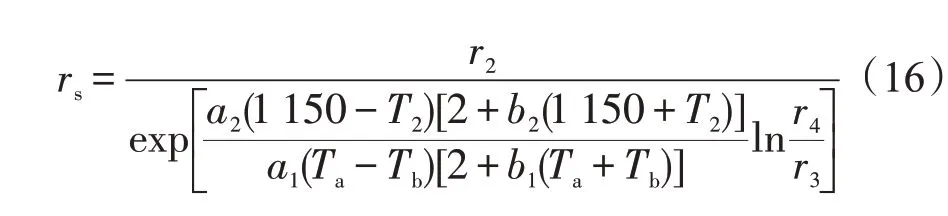
2 移动边界法搜索过程

在确定初始侵蚀边界后，需要不断调整各控制点的坐标，使模型的铁水凝固边界和内衬侵蚀边界逐步逼近真实的凝固边界和侵蚀边界［15］，满足式（1）。当热电偶测量值低于前一次测量值时，铁水凝固边界向炉缸内侧移动（凝铁层变厚），内衬侵蚀边界不变。当热电偶测量值高于其前一次测量值时，可分两种情况：若热电偶测量值低于最大值，铁水凝固边界向炉缸外侧移动，内衬侵蚀边界不变；若热电偶测量值高于最大值，铁水凝固边界和内衬侵蚀边界重合，并同步向炉缸外侧移动［16］。

收敛判定条件

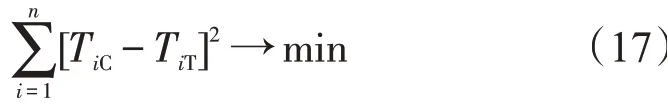
等价于收敛判定条件为

对于不同的高炉，要求的计算精度不同，应视具体情况而定，通常可取e≤2%～5%［17］。

内衬的侵蚀是连续的，假设在一天的时间内，铁水凝固边界和内衬侵蚀边界的变化量都不大（凝铁层大量坍塌等特殊情况除外），可将有解域范围缩小到位于初始边界附近的一定范围内，达到加速收敛的目的。之后采用两分法进行进一步搜索，直到计算结果满足所需精度要求为止。

2.1 缩小有解域范围

以炉缸侧壁为例来介绍缩小有解域范围的方法。内衬剩余厚度越薄，即侵蚀半径越大，其热阻越小，计算值越大［18］。即模拟值TiC是控制点半径的单调递增函数，如图4所示。控制点的搜索方向根据模拟值TiC和实测值TiT的相对大小确定，记

图4 缩小有解域示意图Fig.4 Schematic diagram of reduced solution domain

如果fi＜0，控制点向炉缸外侧方向搜索；如果fi＞0，控制点向炉缸内侧方向搜索。

假设初始边界控制点的半径为ris，Δri0为搜索步长，取Δri0=30～40 mm，可根据具体情况进行调整。缩小有解域范围的计算流程如下：

（1）判断初始控制点ris对应的计算结果是否满足收敛判定式（19）。若满足，则控制点初始位置ris即为所求位置，结束搜索；若不满足，则转（2）。

（2）计算fi(ris)。若fi(ris)＞0，控制点向炉缸内部移动Δri0，至ris-Δri0位置，转（3）；若fi(ris)＜0，控制点向炉缸外部移动Δri0，至ris+Δri0位置，转（4）。

（3）判断控制点位于ris-Δri0位置时，对应的计算结果是否满足收敛判定式（19）。若满足，则ris-Δri0位置就是所求控制点位置，结束搜索；若不满足，则转（5）。

（4）判断控制点位于ris+Δri0位置时，对应的计算结果是否满足收敛判定式（19）。若满足，则ris+Δri0位置就是所求控制点位置，结束搜索；若不满足，则转（6）。

（5）计算fi(ris)fi(ris-Δri0)。若fi(ris)fi(ris-Δri0)≤0，则有解域范围可缩小到[ris-Δri0,ris]，用两分法继续搜索；若fi(ris)fi(ris-Δri0)＞0，则令ris=ris-Δri0，转（2）。

（6）计算fi(ris)fi(ris+Δri0)。若fi(ris)fi(ris+Δri0)≤0，则有解域范围可缩小到[ris,ris+Δri0]，用两分法继续搜索；若fi(ris)fi(ris+Δri0)＞0，则令ris=ris+Δri0，转（2）。

实践证明，如遇凝铁层坍塌等边界变化较大的特殊情况，所需计算时间有所延长，但总体计算量仍处于可控范围。

2.2 两分法求解

在所有控制点的有解域都缩小到Δri0的范围内后，继续使用两分法在该区间内进行搜索，以求解满足收敛条件的最优解［19］。两分法搜索流程如下：

（1）判断控制点位于ris+Δri0/2位置时，对应的计算结果是否满足收敛判定式（19）。若满足，则ris+Δri0/2位置就是所求控制点位置，结束搜索；若不满足，则转（2）。

（2）计算fi(ris)fi(ris+Δri0/2)。若fi(ris)fi(ris+Δri0/2)≤0，则有解域范围缩小到[ris,ris+Δri0/2]，令Δri0=Δri0/2，转（1）；若fi(ris)fi(ris+Δri0/2)＞0，则有解域范围缩小到[ris+Δri0/2,ris+Δri0]，令ris=ris+Δri0/2，Δri0=Δri0/2，转（1）。

3 移动边界法可行性验证

根据AG-3高炉炉缸结构、热电偶温度数据等参数，利用移动边界法对该炉缸内衬的侵蚀形貌进行预测。该高炉于2020年3月停炉并进行炉缸破损调查，部分侵蚀严重位置的侵蚀状态如图5所示，各位置内衬剩余厚度预测值和实测值见表1。内衬剩余厚度最薄处位于炉缸侧壁第3层环碳的TE108J位置，内衬剩余厚度为260 mm，与预测值一致；内衬剩余厚度次薄处位于炉缸侧壁第5层环碳的TE110E位置，该位置左侧碳砖余厚300 mm，右侧碳砖余厚330 mm，预测值为360 mm，计算偏差为30～60 mm；其它位置的偏差不超过80 mm，可满足工程中对炉缸安全状态判断的要求。

图5 AG-3号高炉炉缸部分位置侵蚀形貌Fig.5 Erosion profile of blast furnace hearth in AG-3

表1 内衬剩余厚度的预测值和实际值Tab.1 Predicted and actual thicknesses of remaining lining

4 炉缸内衬安全厚度

炉缸内衬的侵蚀具有不可避免性，随着冶炼的进行，其厚度会不断减薄，安全风险不断增加。造成事故原因可大致分为两种：一是内衬减薄，热阻减小，导致冷却壁产生热损伤，冷却水流入炉缸后，导致内衬破裂烧穿引发爆炸事故。二是在内部压力作用下，内衬破裂。因此需从冷却壁安全热负荷和内衬应力安全强度两个方面确定内衬的最小承载厚度。

4.1 炉缸结构安全所需内衬安全厚度

在正常生产过程中，内衬等材料受热、受压欲向外膨胀，炉壳以反作用力对这种膨胀进行约束。以单层内衬为例，其受力情况如图6所示，内外表面承受压力分别用p和pk表示。

图6 内衬受力示意图Fig.6 Schematic diagram of stress on lining

内衬热面压力p由铁水自重压力pg和风压pw两部分组成，即

式中：ρ为铁水质量密度；g为重力加速度；h为铁水液面到计算部位的深度。

内衬外缘不被破坏的强度条件为

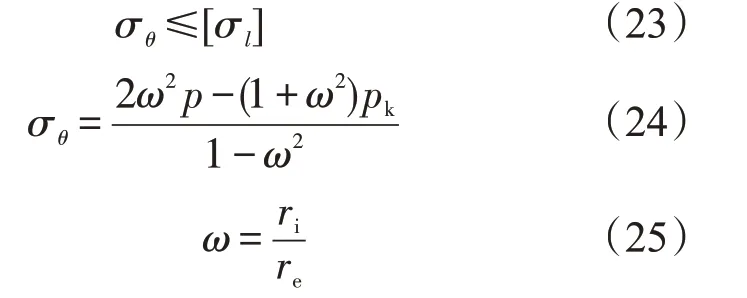
式中：σθ为内衬外缘的环向拉应力；[σl]为内衬的抗拉强度；ω为尺寸比；re为内衬外边缘半径；ri为内衬内边缘半径。

内衬的厚度为

圆筒炉缸内衬的承载安全厚度Lp

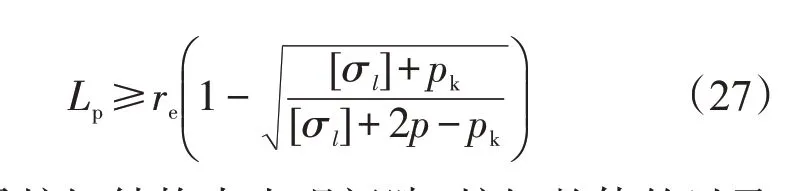
如果炉缸结构中出现间隙，炉缸整体的过盈接触状态将被破坏，炉壳对内衬的紧箍约束作用消失。此时，承载安全厚度Lp应按内衬独自承受内压的情况计算，即

4.2 冷却壁热稳定性所需内衬安全厚度

为保证炉缸冷却壁正常工作，取300℃作为铸铁冷却壁的热稳定温度，150℃作为铜冷却壁的热稳定温度。

利用传热理论推导出满足冷却壁热稳定性要求的内衬安全厚度LT为

式中：λ为内衬导热系数；RT为满足冷却壁热稳定性要求的内衬最小热阻；Ts为内衬热面温度，取1 150℃；Tc为需要维持的冷却壁热面温度；Tw为冷却壁中冷却水的平均温度；RL为冷却壁热面与冷却水之间的总热阻。

4.3 炉缸内衬安全厚度

炉缸侧壁内衬的安全厚度Ls应综合考虑式（28）和式（29），取其中的大值，即

如遇砌筑材料质量不佳、炉缸设计结构不合理、施工质量差等特殊情况，应在式（31）的基础上乘以一个大于1的安全系数。

5 结论

利用数值求解方法，结合预埋在炉缸内衬中热电偶测得的温度数据，提出一种可同时计算内衬侵蚀边界和铁水凝固边界的移动边界搜索方法，推导出初始侵蚀边界位于碳砖层或陶瓷杯层的侵蚀边界计算式。通过AG-3号高炉的破损调查发现，内衬剩余厚度最薄位置的实测值为260 mm与预测值基本一致，其它位置的计算偏差不大于80 mm，证实移动边界法的可行性，该计算方法可满足炉缸安全状态判断的要求。最后从冷却壁安全热负荷和内衬应力安全强度两个方面确定内衬的最小承载厚度计算式，该方法可综合评估炉缸的安全风险。