固定翼无人机编队构型与通信拓扑优化
徐星光, 王晓峰, 姚 璐, 任 章
(1. 北京机电工程研究所, 北京 100074; 2. 北京航空航天大学自动化科学与电气工程学院, 北京 100191;3. 复杂系统控制与智能协同技术重点实验室, 北京 100074)
0 引 言
编队构型设计体现固定翼无人机任务需求多样性,通信拓扑优化是平衡协同控制、网络通信性能、集群隐蔽性的信息交互基础。基于现代优化理论和智能算法,需要分析影响集群综合作战效能的队形与网络通信设计关键指标,建立优化模型。特别地,在飞行速度日益加快、飞行任务不断丰富的需求背景下,优化模型对关键指标的覆盖程度、计算实时性、部署实用性问题愈加重要。为适应复杂高强度对抗环境,攻防双方集群编队规模均可能呈几何增长,这将给飞行器队形与网络连通性在线设计带来成倍计算复杂度,而飞行器计算资源与通信带宽有限,因而如何在确保优化准确度基础上提升规模编队下计算速度是编队构型与拓扑优化问题中面临的一个难点。所以,如何建立编队构型与通信拓扑指标体系,如何设计考虑攻防对抗态势与最小信息流要求的优化模型,并保证计算精度与实时性均衡,是首先要解决的关键问题。
多飞行器编队构型与通信拓扑优化问题是指在满足各种规范和某些特定要求的前提下,使编队在空间域物理构型、信息域通信拓扑的某种广义性能指标最佳,在所有可用的协同方案中找出飞行器在编队中的最优站位,同时减少总的通信代价。编队构型与通信拓扑设计具有重要应用价值,为多飞行器联合执行任务提供了关键理论支撑。据美国海军官网报道,2021年6月,美国在伊利诺伊州成功完成“黄貂鱼”MQ-25A无人机技术验证机向F/A-18“超级大黄蜂”有人机的空中加油测试,这种空中云台的实现很大程度上源于针对加油任务优化出了多飞行器队形及成员飞行器在编队中的站位。解决编队构型与通信拓扑优化设计问题的关键是建立全面准确的数学模型,优化设计研究方向涵盖设计变量选择、约束条件分析、目标函数设计和优化算法计算。下面从多飞行器编队构型、通信拓扑设计优化方面对现有文献加以概述。
编队构型设计变量分为拓扑、形状与尺寸变量。按照工程实际应用的项目阶段划分,概念设计阶段可进行拓扑优化,由编队规模建立优化的框架与层级;基本设计阶段可进行形状优化,明确编队的基本队形组成的数量、形态;详细设计阶段开展尺寸优化,调整预先确定的队形形状长度、角度特征。有关学者针对不同设计变量优化方式取得了一系列成果。文献[2,4]针对大规模固定翼飞行器提出了多层规划模型的拓扑优化框架,将整体队形优化问题转化为分层节点排布对比分析问题,通过改进粒子群优化(particle swarm optimization, PSO)算法及遗传算法求解出最优队形,并给出了相对整体队形优化的计算实时性优势。文献[5-6]借鉴雁群编队飞行行为机制,将“V”形编队构型引入到无人机群协同飞行中,设计纵向、横向距离参数增升减阻,经仿真算例证明了减少燃油消耗量的效果。文献[7]设计了直线、菱形、半菱形、“V”形队形,通过不同编队规模下的流体力学仿真给出了适用一类翼身融合飞行器的减阻阵列选型建议。文献[8]针对有翼飞行器给出了编队合围跟踪队形,为攻击、侦查、诱饵功能提供集成框架。
在设计编队构型时,有必要考虑队形的基本约束问题。队形约束主要包括但不限于两方面原因:一是队形参数在实际通信环境中存在取值上下限;二是队形合理性要有效衔接编队控制的可实现性。文献[9]在构建飞行器编队协同作战效能指标时引入飞行器间最大通信距离、最小安全距离、最大搜索半径、最大搜索角、最大机动半径等参数约束,并采用PSO算法优化出合适队形。文献[10]结合一般线性系统动力学特性给出了分段连续可微编队向量形式和编队可行域扩展算法,之后在切换拓扑下提出了基于一致性方法的时变编队控制器,为无人机系统实际应用奠定理论基础。
为了实现飞行器编队综合效能最大化,国内外学者在设计编队构型时充分考虑战场态势信息和飞行器编队状态以构造综合目标函数。文献[13-14]基于敌我对抗态势建立了敌我战损比目标函数,采用遗传算法优化队形设计,并对空中作战平台对抗过程中的队形适应性进行了验证。文献[1]利用弹目间的战术几何关系,建立了涵盖任务载荷配置、捕获概率、角度优势、速度优势、距离优势的综合优势函数,采用禁忌搜索与离散PSO算法对多弹协同打击目标群的作战构型寻优。
优化算法选择是编队构型优化设计的另一个重要问题,方法选择的主要依据包括计算准确性与时间复杂度,重点是针对特定模型探索工程适用性强的手段。文献[15]采用基于均值漂移的差分演化算法设计了飞行器编队协同突防-攻击一体化队形,该队形兼顾了协同突防和协同攻击需求。文献[16]针对大规模直升机空战编队问题,采用遗传算法进行优化。文献[17]在随机散布建筑物威胁的数字地图下,采用改进PSO算法获得收敛速度与优化质量满足要求的无人机站位。
飞行器在编队飞行过程中只需部分通信链路即可实现队形控制,该部分通信链路为队形保持情况下的通信拓扑,属整个通信网络子集,这就为给定编队构型前提下减少通信路由代价提供了理论支撑。目前针对通信拓扑构成形式方面已有一定成果,以编队控制方法为依据,通信拓扑具体包括:面向领导者-跟随者编队控制策略,采用通信网络中一颗有向生成树;面向行为或虚拟结构编队控制策略,采用通信网络中一个双向环;面向基于一致性的编队控制策略,采用的通信拓扑至少一个子集隶属通信网络的一颗有界生成树。
在通信拓扑约束条件分析方面的研究成果集中在3个方面:一是编队控制方法约束;二是领导者飞行器约束;三是通信链路故障约束。文献[11]分析了四旋翼无人机通信拓扑构建条件,考虑基于一致性的编队控制策略,提出如切换通信拓扑每个子集存在一条从领导者到跟随者的生成树,则可以实现稳定的编队跟踪队形,并给出了具有1个领导者和3个跟随者的四旋翼无人机飞行实验。文献[18]分析了不同领导者无人机站位约束下的编队通信拓扑构建问题,提出了编队领导者节点等效交换算法。文献[21]研究了编队跟踪队形下的通信质量与考虑领导者未知运动约束的协同控制律之间的关系,从中可以看出对领导者飞行器的机动位置估计偏差,会产生生成树丢失风险。
通信拓扑的优化目标是在保证任务成功率基础上降低编队通信代价。文献[22]将通信链路数量作为通信拓扑生成目标,但没有考虑不同无人机之间通信链路对应通信代价的不同。文献[23]考虑了通信路由赋权问题,提出最优持久编队。文献[24]提出了一种通信能耗均衡的三维最佳持久通信拓扑生成算法,将优化目标函数设计为从网络拓扑中选择合适的子集,使得各智能体中通信剩余能量持续时间最大化,之后引入离线优化算法进行迭代估计,通过理论分析与仿真算例验证了计算复杂度与求解质量。
优化与决策理论在通信拓扑最优求解方面应用广泛。文献[25-26]采用Dijkstra最短路径算法优化领导者-跟随者编队飞行框架下的通信拓扑。文献[27]采用两种不同的Nesterov加速算法,提出分布式加速最快梯度下降理论,下降收敛速率优于集中式方法,满足通信网络高度动态变化的航空适用需求。文献[28]在大规模异构无人机集群通信网络多边稳定匹配问题上,提出了双层稳定匹配分布式优化算法,通过与差分进化算法的对比仿真证明了所提方法在求解速度与质量方面的优越性。此外,研究人员将粒子群算法、蚁群算法、萤火虫算法应用到无人机动态组网路由优化配置中。
本文研究了考虑攻防对抗态势与最小信息流要求的编队构型与拓扑优化问题,主要贡献如下:针对高动态任务背景下多固定翼无人机在空间域、信息域快速优化问题给出了优化算法;针对编队构型优化提出了基于态势场的分层编队构型结构优化方法;针对通信拓扑优化提出了基于Q学习的网络连通性控制方法,解决了考虑攻防对抗态势与最小信息流要求的编队构型与拓扑优化问题,实现了兼具快速性与全局最优性的大规模编队构型及拓扑优化效果。
1 模型建立
1.1 编队构型建模
考虑架固定翼无人机通过通信拓扑连接而成的一个多无人机集群系统,按照编队构型()进行时变编队协同飞行。通信拓扑中的边意味着无人机和无人机之间能够进行相互通信。结合固定翼无人机作战任务,建立编队构型效能指标体系,用以定量、准确评估编队构型参数对无人机集群系统协同编队任务的影响。
本节的主要目的是综合考虑战场态势信息与无人机自身特性,面向图1所示的编队构型效能最大化,设计满足计算精度与实时性要求的多无人机编队构型优化模型,并有针对性地开展选型定参工作。考虑集群作战网络规模大,提出了分层编队构型结构模型,将无人机集群编队进行分层,集群分层的每个节点均可表示一种基本编队构型,最终得到整个无人机集群的设计队形。
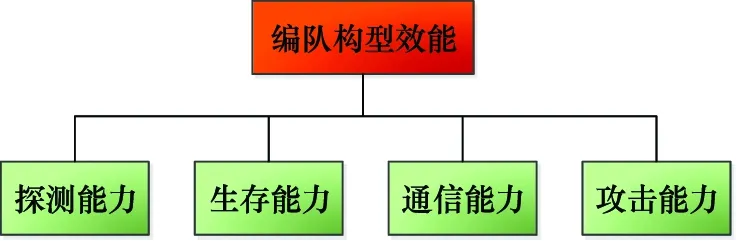
图1 编队构型效能指标体系Fig.1 Formation configuration efficiency index system
根据编队构型的任务需求与工程实现,将三维编队构型分解为水平和垂直两个平面上的二维队形,通过基本队形组合形成立体协同编队态势。基本队形共设计8种,采用二进制编码对编队进行编码,具体如表1所示。
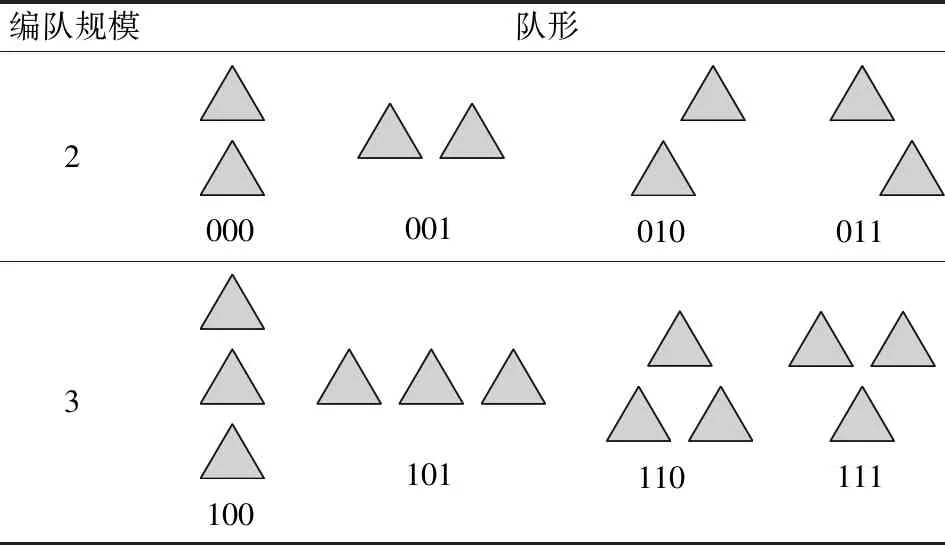
表1 基本队形及其编码表Table 1 Basic formation and its coding table
集群系统中固定翼无人机数量众多,一般由多种基本编队构型组成,编队规模较大,为便于解析化描述,引入分层编码解码机制。针对网络规模为的无人机集群系统,对编队自顶向下进行共计(>1)层的分层划分,直至不同分层获得基本编队构型,在第层得到最小编队单元,在编队结构体系构建过程中按照每层构建次序得出编码序列。反过来,由编码表对特定编码序列进行依次解码,反演获得分层编队构型。在编解码过程中,根据各层节点中队形在其上层节点队形中的排布方式,按照从上到下、从左向右顺序进行编码和解码,如图2所示。

图2 分层编队构型编解码过程Fig.2 Hierarchical formation coding and decoding process
选取编队整体位置的几何中心作为领导者无人机,上述位置无实体无人机时称为虚拟领导者无人机。以上述几何中心作参考点,描述不同基本队形的具体设计参数,记为
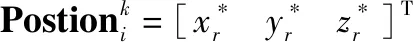
(1)
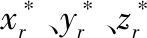
固定翼无人机态势场模型主要考虑无人机探测能力、生存能力、通信能力、攻击能力等4方面因素,第架无人机态势模型为
=(,,,,,)=(++)
(2)
式中:(,,)表示地面坐标系下无人机的位置坐标;(,,)表示地面坐标系下对抗目标的位置;表示无人机的探测能力;表示无人机的攻击能力;表示无人机的生存能力;表示无人机的通信能力;、、分别表示攻击能力、生存能力、通信能力的权重值,采用三角模糊数指标权重求解方法确定。
(1) 探测能力
固定翼无人机根据任务需求配装不同功能的任务载荷,针对对抗目标的探测设备主要包括雷达和红外搜索跟踪装置,探测能力模型如下:
=ln(1+)
(3)
式中:表示无人机的探测能力参数,具体表达式为
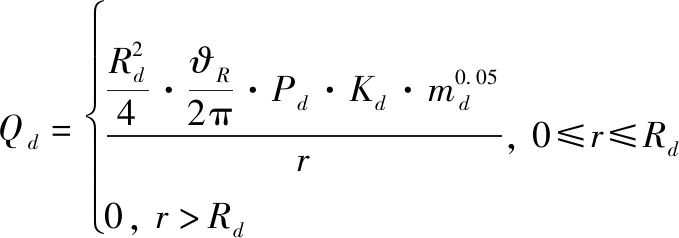
(4)
式中:表示末制导设备最大作用距离;ϑ表示末制导设备最大搜索方位角;为对抗目标捕获概率;为末制导体制衡量系数;为末制导可同时跟踪的对抗目标数量。
(2) 攻击能力
攻击能力模型为
=ln(1+)
(5)
式中:表示无人机的攻击能力参数,具体表达式为
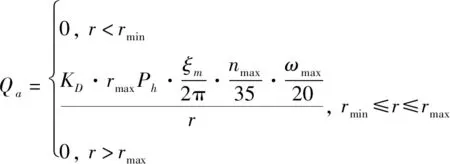
(6)
式中:为制导方式修正系数,半主动雷达末制导=1,主动雷达末制导=15;为无人机单发命中概率;为无人机攻击范围角;为无人机最大可用过载;为无人机最大跟踪角速度;为无人机距计算点的距离;为无人机最大射程;为无人机最小攻击距离。
(3) 生存能力
无人机生存能力模型建立如下:
=ln(1+)
(7)
式中:表示生存能力参数,具体表达式为
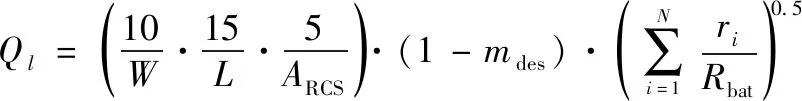
(8)
式中:为无人机长度;为无人机翼展;为雷达发射面积;为易损系数,0<<1;表示战场环境控制区域最大距离。
(4) 通信能力
无人机协同编队通过编队支撑网络实现信息交换和共享,通信能力实现载体为数据链设备。数据链通信品质与无人机间距离相关,建立通信能力模型如下:
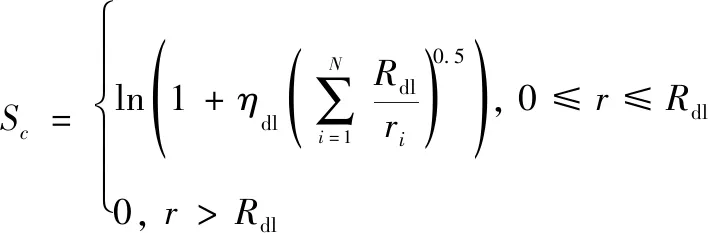
(9)
式中:为数据链设备的可靠性;为数据链最大通信距离;为与第架无人机的距离。
(5) 交换比
为表征编队规模对综合效能的影响,引入交换比概念,表征无人机集群系统在完成特定任务时收益与资源投入比较。设己方一架无人机作战成本为cos (),则可定义交换比为

(10)
则在整个战场环境下,己方无人机集群编队系统产生的态势场由不同节点成员在空间中的态势叠加而成,具体表达式为
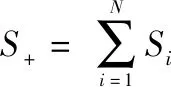
(11)
节点平均态势为
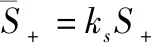
(12)
在无人机集群编队对抗目标过程中,拦截方考虑部署个节点,按照上述公式同理可计算拦截方态势场如下:
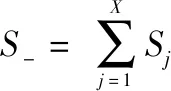
(13)
战场空间中拦截方部署情况包括离散的先验已知威胁和仅获取概略情报的非合作概率威胁,故在选取适应度函数表征无人机编队效能时,应将战场环境内概率威胁进行建模,基于态势场的无人机队形适应度函数为
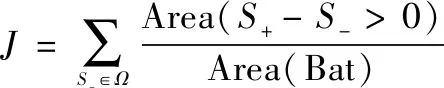
(14)
式中:Area(->0)表示己方态势场大于敌方态势场的战场环境局部面积;Area(Bat)表示战场环境整体面积;表示拦截力量部署的概率分布区域。
1.2 通信拓扑建模
固定翼无人机主要通过数据链实现信息交互,按照有无信息中继平台,通信链路可以划分为无人机-星-无人机、无人机间两种形式。涉及无人机间协同组网通信的研究成果,主要从控制与通信两方面分立开展,对于协同制导控制框架下对通信拓扑的反向设计研究结果较少。
本节从协同控制的最小需求出发,从适用编队控制协议一般性的角度,给出通信拓扑需要满足的最小条件。
在固定翼无人机执行协同编队任务过程中,各成员通过无人机间信息交互形成的通信拓扑最小条件是,包含一条生成树的有向图,且根节点为虚拟领导者无人机。
为定量准确评估通信网络建立路由过程对无人机集群系统协同编队任务的影响,建立通信网络拓扑参数效能指标体系,如图3所示。

图3 通信网络拓扑参数效能指标体系Fig.3 Performance index system of communication network topology parameters
本节的主要目的是提出自主、智能的网络连通性控制算法,对节点间连通情况进行优化设计,使得无人机集群系统在编队协同控制基础上,实现路由低开销,在提升通信强度和降低被敌方发现概率间优化,得到最佳匹配。
针对固定翼无人机集群系统成员向成员构建通信链路的过程,建立无人机通信网络路由模型,主要涉及通信强度、通信链路成本、端机功耗和被敌探测概率等四方面因素,具体如下:
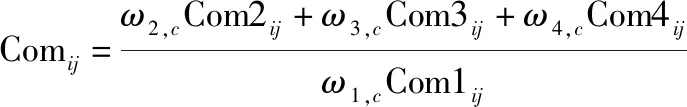
(15)
式中:Com1表示通信强度;Com2表示通信链路成本;Com3表示端机功耗;Com4表示被敌探测概率;1,、2,、3,、4,分别表示通信强度、通信链路成本、端机功耗、被敌探测概率的权重值,权重由三角模糊数指标权重方法解算。
(1) 通信强度
集群系统编队协同的首要基础之一是建立较强的通信能力、信息感知能力,以实现高效的数据传输与信息共享。通信强度模型为
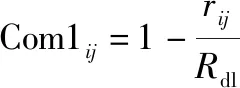
(16)
式中:为成员与成员间距离;为无人机间数据链最大作用距离。
(2) 通信链路成本
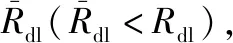
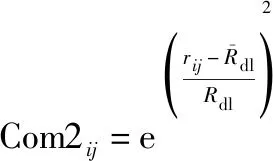
(17)
(3) 端机功耗
数据链端机作为通信网络在无人机端侧部署的载体,在高动态工作条件下需无人机提供大量能源,功耗与数据链作用距离和通信带宽有关。端机功耗模型如下:
Com3=ln(1+Wt)
(18)
式中:Wt表示无人机的端机工作功率,具体表达式为
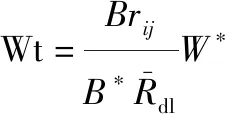
(19)
式中:代表通信带宽;为标准状态下通信带宽;表示标称状态下端机功耗。
(4) 被敌探测概率
在无人机数据通信中产生的电磁信号会作为敌侦查探测的目标电子特征信息,与通信强度、端机功耗、工作频段相关,建立被敌探测概率模型:
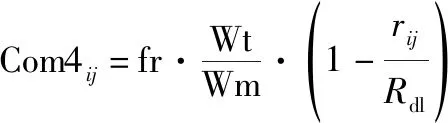
(20)
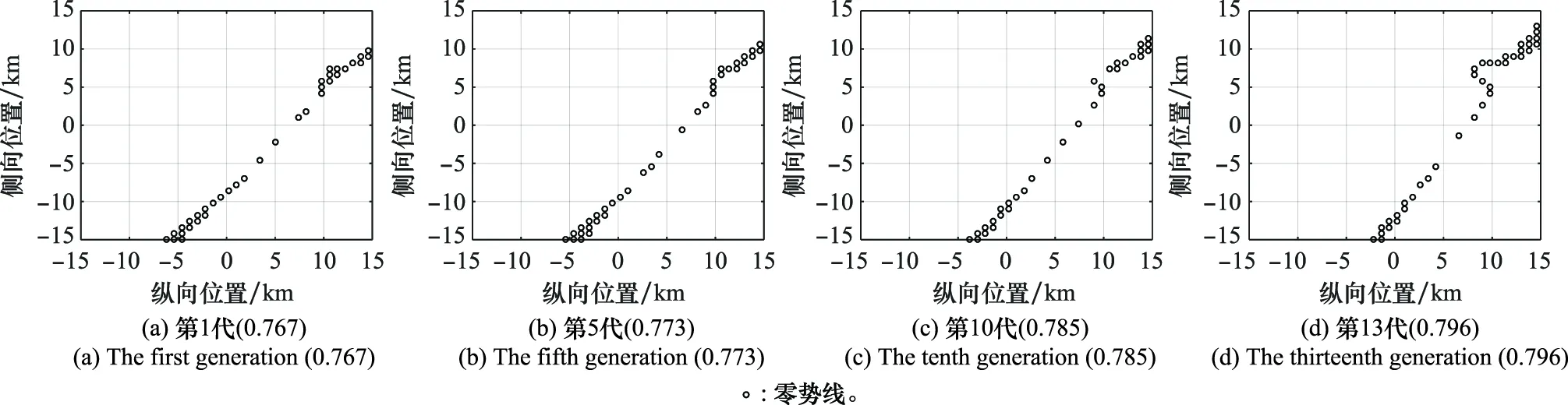
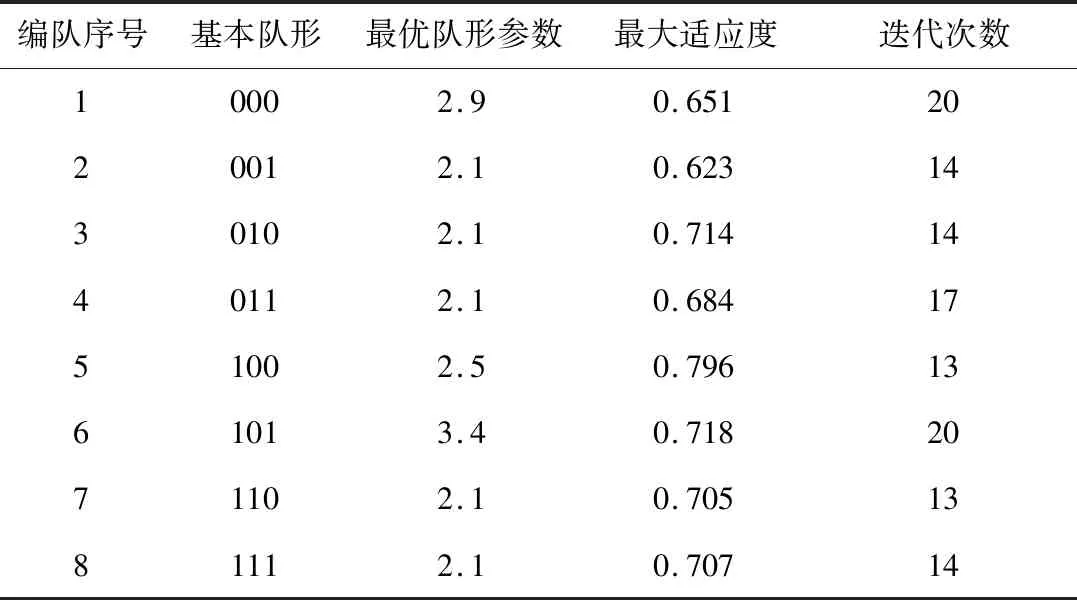
式中:fr为频段系数,0 下面基于PSO算法,给出网络规模为的固定翼无人机集群系统编队构型参数设计方法。 算法1 固定翼无人机集群系统编队构型参数设计方法 步骤1 在首层分别进行8种基本队形的节点平均态势场计算,采用PSO算法优化编队构型参数,计算每种基本队形下适应度最大的队形参数,对比分析后择优选取。步骤2 计算最优基本队形各实体单元坐标,作为下一层节点最优队形站位的中心位置。在下一层采用PSO算法开展队形选型定参工作,确定本层采取的基本队形与队形参数。步骤3 重复步骤2,直至队形分解的无人机数量达到N。步骤4 整合各层级队形优化结果,得到全局队形优化方案。 随着编队网络规模的增加,通信网络可建路由数量庞大,如采用基于规则的路由设计方法对式(15)进行优化,将给专家系统和计算实时性带来较大负担。本节在网络路由过程中引入强化学习技术。 接下来需要给出网络连通性控制方法,通过多轮迭代的Q学习策略寻找各网络节点的最优行动值,即选取相应的最优路由方向。 本节旨在建立固定翼无人机集群系统的网络通信关系,路由过程遍历各编队成员,选择状态量对应编队规模,记状态空间={1,2,…,}。每个成员无人机周边的邻居节点作为行动空间的变量。(,)为初值为任意值的二维空间。每个成员无人机,需要找到最佳的路由方向,使得通信网络拓扑参数效能最优。 根据假设1,路由的最终目标是建立从领导者无人机到当前节点的有向路径。节点与领导者无人机可建立直接通信链路时,需要获得最大奖励,故回报函数设为;节点可与周边邻居建立多跳关联时,需要获得最佳网络通信路由,故回报函数设为Com。策略选择机制方面,采用贪婪策略来探索新的动作序列。 算法2 基于Q学习的网络拓扑优化方法 步骤1 根据固定翼无人机集群系统不同节点间距离,结合数据链建立链路的距离限制,建立无人机可建最大通信拓扑,计算初始状态的累计回报Q矩阵:Qij=0,rij≤Rdl-1,rij>Rdl{步骤2 针对整个无人机编队中某一节点i,将其状态初始化为si,将其预处理成与Q网络的输入结构相同。步骤3 回报函数的计算fR(s,a)=Fmax,(v0,vj);j=1,2,…,NFmaxComij,(vi,vj);j=1,2,…,N;i≠0ìîíïïïï式中:建立领导者向某节点通信链路时,表示为(v0,vj),回报函数取Fmax。建立其他通信链路时,表示为(vi,vj),回报函数取Fmax/Comij。步骤4 动作设置与优化根据无人机可建路由行动空间,将临近节点作为建立链路的可选动作,选择Q值最大的动作,获得即时奖励fR(s,a),并进而完成Q值的更新:Q(st+1,at+1)=(1-α)Q(st,at)+α[fR(st,at)+γmaxQ′(st+1,at+1)]步骤5 重复执行步骤2~步骤4,直至Q网络收敛。步骤6 选择距离领导者无人机最远的节点,根据Q矩阵推理获得最优动作,建立通信主链路。步骤7 如通信主链路涵盖所有成员,计算结束;如存在通信主链路外成员,则此无人机选择最短路径与通信主链路建立路由,形成整体网络通信拓扑。 在本节中,将对编队规模为8的察打一体固定翼无人机集群系统,遂行30 km×30 km战场环境范围内的目标群对抗任务,进行编队构型与通信拓扑优化。战场环境在地面坐标系平面内栅格化成300×300区域网格,各固定翼无人机性能指标见表2。存在规模=5的拦截编队,其位置部署在3 km×2 km的概率分布区域内,如图4所示。虚拟领导者无人机处于编队集群中心位置,仿真初始时刻位置=-1 200 m,=12 250 m,=-500 m,航迹倾斜角=0°,航迹偏转角=0°,初始速度为250 m/s。虚拟领导者无人机朝向动态集结点飞行,集结点初始位置为战场原点,速度=50 m/s,=0,=50 m/s。要求虚拟领导者无人机在飞行末段实现带有攻击角度约束的入射,期望角度设计为=0°、=45°,跟随者无人机以虚拟领导者无人机为中心建立期望的编队构型与通信拓扑。 表2 固定翼无人机性能指标Table 2 Fixed-wing UAVs performance indicators 图4 战场环境部署Fig.4 Battlefield environment deployment 针对虚拟领导者无人机运动轨迹,亦即固定翼无人机集群系统整体运动参考轨迹,在地面坐标系下、平面内采用鲁棒自适应制导律求解。设定虚拟领导者无人机到达集结点的条件为偏移量小于1 m。仿真结果如图5所示,虚拟领导者无人机最终以距离集结点0.045 m的偏移量实现带有攻击角度约束的入射。虚拟领导者无人机运动设计过程不是本文研究重点,这里仅给出设计结果。 图5 虚拟领导者无人机运动曲线Fig.5 Virtual leader unmanned aerial vehicle motion curve 针对跟随者无人机站位设计,在飞行不同时刻均以虚拟领导者无人机为中心构建编队构型。取=5.35 s开展基于态势场的分层编队构型设计与优化,来验证本文算法的实际效果,此时虚拟领导者无人机位于图4所示战场区域原点。对于第1层,建立8种基本队形的态势场模型,假设编队成员距离在1~6.5 km范围内,应用PSO算法优化编队构型,使用规模20的粒子群迭代30次。图6绘制出了编队规模为2的010基本队形、编队规模为3的100基本队形的参数优化过程,其余基本队形演化曲线与这两种队形相似。从图6可以看出,本算法能在20次迭代范围内搜索到模型的最优解,有效解决编队构型快速优化问题。从图7可以看出,针对基本队形100,随优化迭代进程,零势线不断向对抗目标区域压缩,编队构型对战场态势的控制效益不断提升,态势场由最初的0.767逐步增长为0.796。 图6 编队构型优化过程Fig.6 Formation configuration optimization process 图7 基本队形100下态势场演化过程Fig.7 Evolution process of situation field under basic formation 100 编队构型优化过程见表3和图8。可以看出,在第1层,从8种队形中选出最优基本队形100,队形参数经迭代优化设置为2.5时,可获得对战场空间0.796的控制比例。继续运用基于态势场分层编队构型优化算法完成第2层、第3层计算,得到的编队构型最终结果见表4和图9,其中“—”表示上一层级已在本节点分层结束,本层级不作分层。 表3 第1层不同基本队形迭代优化过程Table 3 The 1st iteration optimal process of different basic formations 图8 第1层不同基本队形的适应度直方图Fig.8 The 1st fitness histogram of different basic formations 表4 优化队形参数Table 4 Optimization of formation parameters 图9 编队构型优化结果Fig.9 Optimized result of formation configuration 为证明本策略兼顾队形全局优化和计算实时性的优势,对于同一种仿真场景,采用整体队形优化的方法对固定翼无人机集群编队构型进行优化,最终得到与图9基本一致的最优队形。采用整体法时的PSO算法的适应度曲线如图10所示,可以看到适应度收敛到一个最大值,说明整体法能得到最优解,而由分层编队构型算法计算的队形与整体法相似,检验了分层算法计算精度的有效性。但是,因集群整体队形复杂,迭代1次耗时5 ms,适应度计算时间约为6.325 s,远大于分层算法1.935 s的计算时间,证明了本文算法在时间复杂度方面的优势。 图10 整体优化与本文算法对比Fig.10 Comparison of global optimization and the proposed algorithm 在不同网络连通性配置下,本节基于网络通信路由模型对所提理论、其他路由策略的通信性能进行仿真对比,对所提算法优越性进行验证。针对仿真场景中编队规模=8的固定翼无人机集群编队,采用算法2生成最小信息流网络拓扑连接。图11描述了网络可建路由分支为17的设定下无人机通信网络训练空间,节点1~8表示各跟随者无人机,节点9代表虚拟领导者无人机。以4号无人机为例,其优化前可分别与3号、6号、8号无人机建立通信路由,通过Q学习策略对最优路由策略寻优的训练过程如图12所示。可以看出,在前70个训练周期中,4号无人机与其余无人机的路由效果存在持续波动现象,这是由于在这个阶段,值网络输出以探索各种可能的策略为主。经过前70个训练周期后,值网络对整个样本空间进行了相对全面的采样。基于采样数据,通过训练不断对值进行泛化,直至趋近于常数。与3号(蓝色曲线)、6号(黑色曲线)、8号(红色曲线)无人机建立路由的稳态值分别为0.67、0.58、0.32。4号无人机据此建立与3号无人机的有向通信链路。其余路由优化过程与4号无人机类似。 图11 可建立路由的无人机编队设定Fig.11 Unmanned aerial vehicle formation available for routing settings 图12 4号无人机Q值网络训练过程及效果Fig.12 Q value network training process and effect of No.4 unmanned aerial vehicle 经优化设计,无人机2、3分别经6、3跳后与虚拟领导者无人机9建立路由,形成通信拓扑主链路,存在一条以虚拟领导者无人机9为根节点的生成树,通信拓扑最终设计结果如图13所示。 图13 通信拓扑优化结果Fig.13 Communication topology optimization results 除了Q学习外,进一步引入扩展场景,和其他两个路由策略进行对比: (1) 随机路由策略:每个固定翼无人机在数据链建立通信范围内随机选择与其他成员建立信息链路; (2) 就近路由策略:每个固定翼无人机与离自己最近的其他成员建立信息链路。 图14对比了不同路由策略,给定不同的网络可建路由分支,每个策略所能实现的最优效果。横坐标为网络可建路由分支,纵坐标为整个网络的通信性能。 图14 不同路由策略在不同设定下的最优表现Fig.14 Optimal performance of different routing strategies under different settings 仿真实验结果表明: (1) 基于Q学习的网络连通控制方法在4种编队规模中(编队规模依次为5、8、12、16)均比其他策略具备显著优势,就近路由策略表现次之,随机路由策略表现最差。 (2) 在网络连通性较低的配置下,由于优化动作空间有限,各个策略在路由选择方面的差距不是很明显,当整个编队空间分布较为聚集时,由于可建路由分支增加,Q学习一直保持明显优势。 进一步考察Q学习的路由策略,从图14可以看出,在可建路由分支满足数据链建网标准的情况下,对任何一种网络分布情况,Q学习均能自动学习出路由分配策略,即综合考虑通信强度与突防性能建立最小信息流网络拓扑,避开通信代价较高的节点链路。算法分析与仿真算例表明,在路由分配问题上,Q学习不仅求解效果优于其他策略,且具备优良的可解释性。 本文研究了固定翼无人机时变编队构型设计及拓扑优化问题,考虑了空间分布与通信拓扑两种优化对象。将无人机划分为领导者、跟随者两类,跟随者无人机以领导者无人机运动轨迹为中心建立编队构型与通信拓扑。在大规模集群编队系统高动态任务需求背景下,提出分层编队构型设计模型,设计队形编解码方法和态势场模型,采用PSO算法进行队形参数优化。针对集群系统通信拓扑构建问题,建立了通信网络路由模型,提出了基于Q学习网络连通性控制算法,解决了协同一致性与网络路由代价的平衡优化。仿真算例验证了本文设计的时变编队构型及通讯拓扑设计优化算法的有效性。2 编队构型与通信拓扑优化算法
2.1 编队构型优化算法

2.2 通信拓扑优化算法

3 仿真实验分析


3.1 编队构型优化仿真



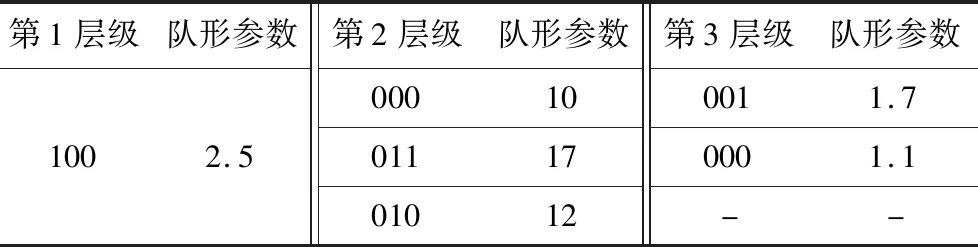

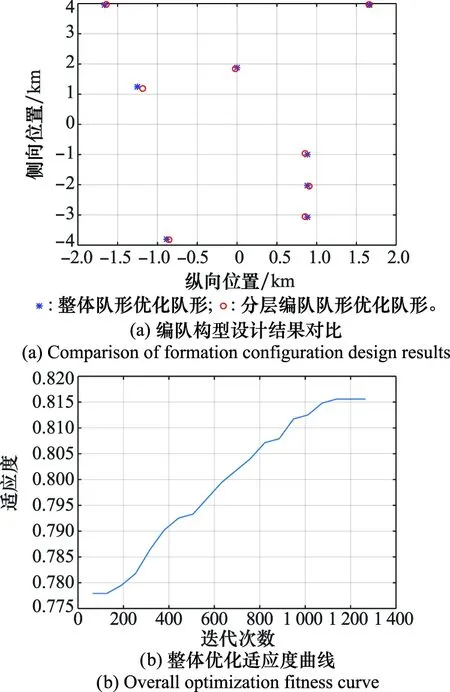
3.2 通信拓扑优化仿真
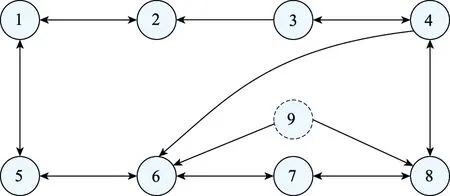
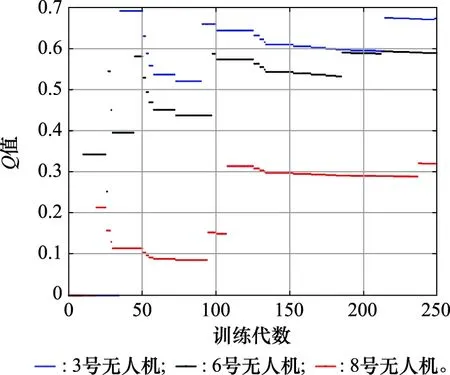
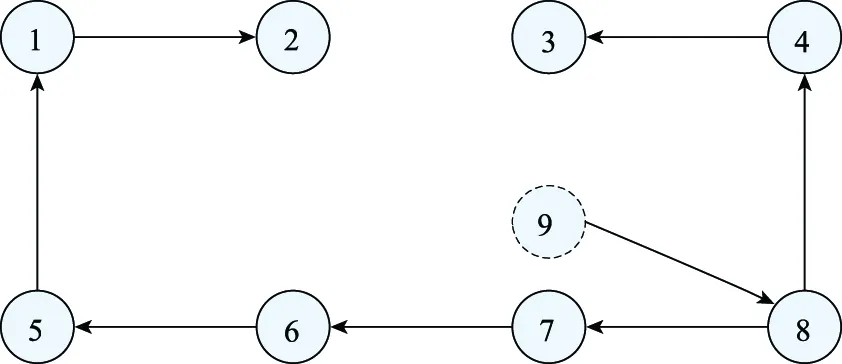
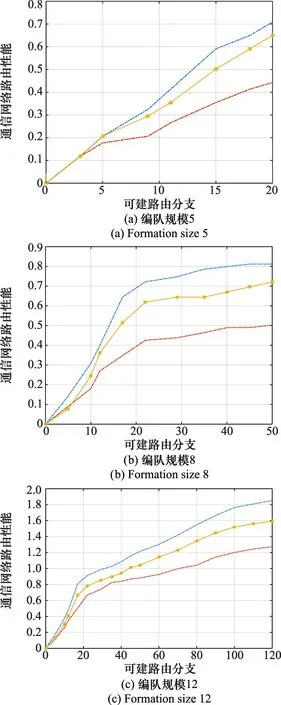
4 结 论

