基于二次补偿的FDA-MIMO雷达抗主瓣欺骗式干扰方法

张逸群, 兰 岚, 廖桂生, 许京伟

(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)

0 引 言

在复杂电磁环境中,雷达系统面临各种干扰,严重制约其对目标信息的准确获取。常见的干扰类型包括压制干扰和欺骗干扰,其中欺骗干扰因其与目标相似性极强而难以抑制的特点被大量采用,尤其当欺骗干扰位于波束主瓣内,采用恒虚警(constant false-alarm rate,CFAR)技术无法检测出目标,对雷达探测带来严峻挑战。目前,针对主瓣欺骗式干扰,学者们从时域、频域、空域等开展了抗干扰研究。文献[13]借助盲源分离(blind source separation,BSS)技术对主瓣干扰进行滤除,但该方法前提是干扰和目标相互独立或者相关性较小,且需要额外的先验知识。另外,频率捷变是一种频域抗干扰的有效方法,文献[15]利用脉冲重复频率抖动和频率捷变相结合的方式发射波形,使得雷达信号难以被截获,然而其不同脉冲间的信号相关性难以保证。传统空域自适应波束形成方法需要获得较为准确的干扰加噪声协方差矩阵,而在实际情况中很难实现。对此,文献[16-17]提出一种基于特征投影及波束赋形的主瓣干扰抑制算法,文献[18-19]基于特征投影矩阵和协方差重构算法对主瓣干扰进行抑制。然而,现有抗干扰方法大多基于传统相控阵雷达体制,其抗干扰效果具有一定的局限性。

频率分集阵(frequency diversity array,FDA)在相控阵基础上,在发射单元之间引入了一个很小的频率步进量,因此其发射导向矢量中包含目标的距离维信息,使得系统具有更高的自由度。通过结合多输入多输出(multiple input multiple output,MIMO)技术,可以通过空域自适应和非自适应波束形成方法有效抑制与真实目标具有距离差异的主瓣欺骗式干扰。进一步,通过对阵元和脉冲同时进行编码也可以有效对抗跨脉冲转发的主瓣欺骗式干扰。在FDA-MIMO雷达中,等效于在发射空间频率域进行干扰抑制。但此类方法的前提是干扰与目标位于不同的距离模糊区间。上述方法能够有效抑制位于下一个距离模糊区间的主瓣干扰,但对于脉内快速转发干扰的对抗能力有限。

本文基于FDA-MIMO雷达体制开展主瓣欺骗式干扰抑制方法研究。首先,对脉内主值距离进行前移补偿来抑制跨脉冲的干扰,再利用脉内真、假目标的距离频率差异进行后移补偿,将脉内快速转发的主瓣干扰搬移到方向图旁瓣。然后,通过奇异谱分析(singular spectrum analysis, SSA)方法挑选样本进行自适应波束形成,实现对主瓣欺骗式干扰的抑制。通过仿真实验验证所提抗干扰方法的有效性。

1 FDA-MIMO信号模型

考虑在采用均匀线阵的共置FDA-MIMO雷达系统中,选取个发射阵元和个接收阵元,且各阵元间距为半波长。则第(=1,2，…,)个发射单元发射出的信号可以表示为

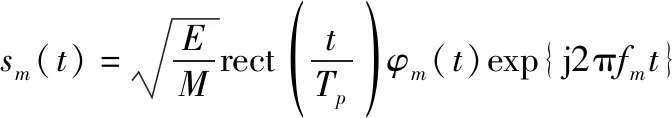
(1)

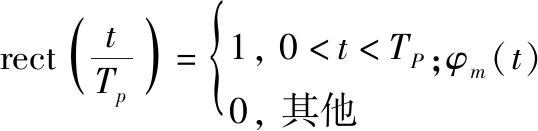
假设远场目标位于角度,距离,则第(=1,2,…,)个接收天线阵元接收到的信号为

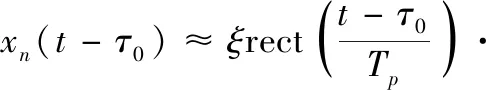
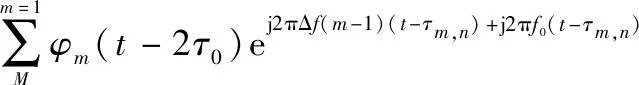
(2)

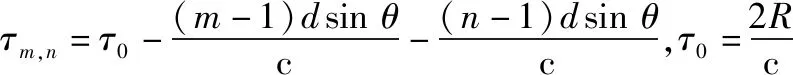
接收信号混频后,首先对频率步进量相关项进行数字混频,再对发射波形进行匹配滤波,则得到总的接收信号的矢量形式为

=[(,),(,),…,(,)]=
[()⊗(,)]

(3)

式中:(,)表示第个接收阵元匹配滤波后的输出信号;符号⊗表示Kronecker乘积；(,)和()分别表示接收和发射导向矢量,如下:

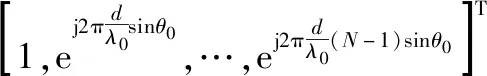
(4)

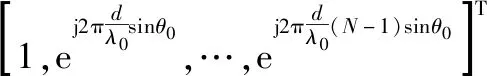
(5)

式中:符号⊙表示Hadamard乘积。

2 基于二次补偿的抗干扰原理

自卫欺骗式干扰机与目标位于同一角度,干扰机将截获的目标回波信号进行调制和延时后转发形成若干假目标,且其绝对位置落后于真实目标。根据转发时延的差异,若时延较大,假目标在下一个脉冲转发形成,此时可以根据真、假目标发射脉冲序号的差异进行鉴别;若时延较小,可根据真、假目标在脉内的距离差异进行鉴别。如图1所示，本方法主要面向脉内(Ⅰ区)快速转发干扰。

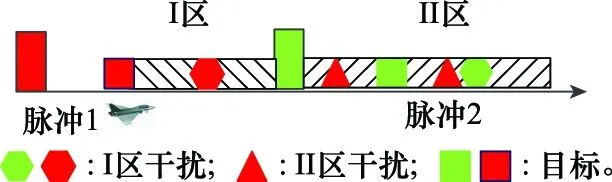
图1 主瓣干扰示意图Fig.1 Schematic diagram of the main-lobe interference

本节提出基于二次补偿的抗干扰方法。首先通过一次补偿(即前移补偿)抑制跨距离周期的转发式干扰;然后通过二次补偿(即后移补偿)的方式将脉内干扰搬移至旁瓣；最后,利用SSA的方法进行样本挑选,并借助自适应波束形成的方式对干扰进行抑制。

2.1 一次补偿(前移补偿)

根据目标发射和接收导向矢量的表达式,可以表示出其发射和接收频率为

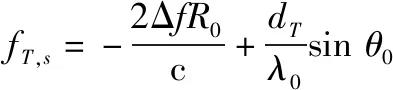
(6)

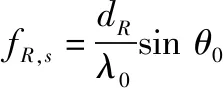
(7)

类似地,对于位于角度、距离处的假目标,其发射和接收频率分别如下:

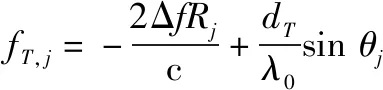
(8)

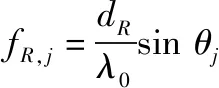
(9)

由于真、假目标角度相同,即=,因此可根据其发射频率的距离分量的差异,即,=-2Δc与,=-2Δc,来对真、假目标进行区分。

针对跨周期的转发式干扰,即考虑距离模糊时,则真、假目标的实际距离可分别表示为

=+

(10)

=+

(11)

式中:表示最大无模糊距离;和分别表示真、假目标的脉内主值距离;和分别表示真、假目标的距离周期数(即延迟的脉冲数)。

首先,构造补偿频率1=2Δc来补偿掉脉内距离频率,其中为由距离门号和距离门大小决定的主值距离。因此,处于同一发射脉冲内所有目标的距离频率与脉内初始距离门所对应的距离频率相等,即实现了前移补偿。此时,在发射空域上不同目标对应的距离频率点由分散变为集中。具体而言,构造发射频率补偿矢量为

=[1,ej2π1,…,ej2π1]

(12)

进一步,构造收发联合前移补偿矢量为

=×1⊗=[1,1,…,1]⊗[1,ej2π1,…,ej2π1]

(13)

随后,利用收发联合补偿矢量对接收数据进行补偿,得到一次补偿后的数据为

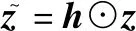
(14)

式中:表示包含真实目标、欺骗式干扰与噪声的总接收数据。则补偿后真、假距离分别为

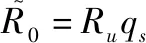
(15)

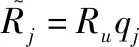
(16)

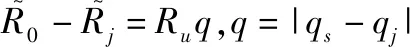
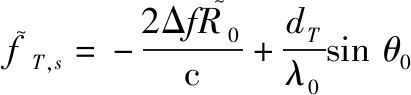
(17)

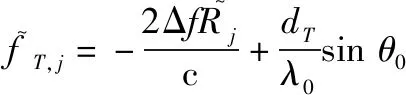
(18)

因此,根据真、假目标的距离模糊数差异,可以对其在发射空间频率域进行区分。

2.2 二次补偿(后移补偿)

尽管采用前移补偿的方式能够区分真实目标与跨脉冲转发的欺骗式干扰,但仍无法区分脉内快速转发形成的假目标。对此,可根据转发的假目标绝对距离大于真实目标这一特点,将真实目标之后的假目标进行空间频率后移补偿,使得假目标的距离频率与下一个脉冲起始点对应的距离频率相同,达到频率后移的效果,即实现后移补偿,如图2所示。其中,真实目标所在的距离门通过样本筛选技术得到。

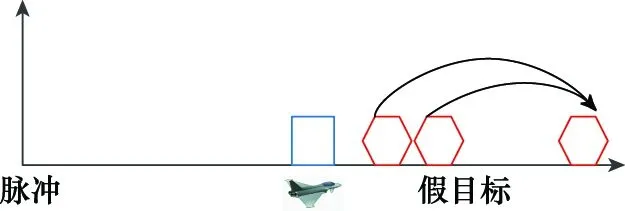
图2 二次频率补偿示意图Fig.2 Schematic diagram of secondary frequency compensation

具体而言,构造二次空间频率补偿矢量为

=[1,ej2π2,…,ej2π2]

(19)

式中：2=-2Δc表示后移补偿频率。进一步,构建收发联合前移补偿矢量为

=×1⊗=[1,1,…,1]⊗[1,ej2π2,…,ej2π2]

(20)

则补偿后的接收数据表示为

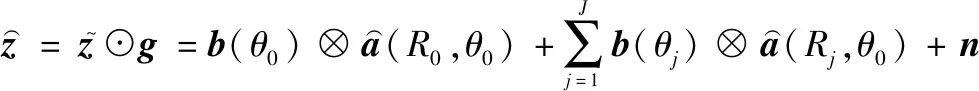
(21)

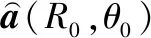
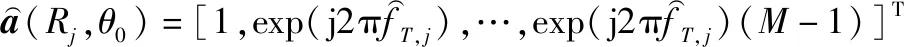
(22)

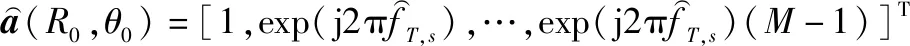
(23)

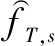
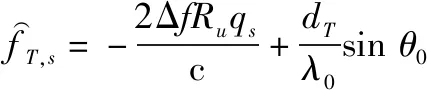
(24)

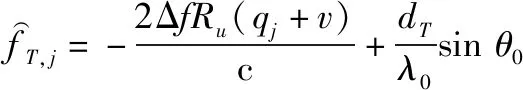
(25)

由于=,则后移补偿后真、假目标存的空间频率差异为

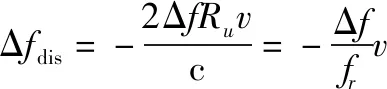
(26)

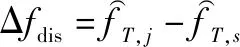
2.3 SSA样本挑选

经过二次补偿后,真、假目标在距离频率上能够区分,利用自适应波束形成技术对假目标进行抑制。然而实际中,由于假目标的伪随机分布特性而不满足独立同分布条件,无法获取准确的干扰加噪声协方差矩阵,对此可借助SSA方法挑选合适的训练样本,得到干扰加噪声协方差矩阵。

根据各距离单元中的回波信息,可构建如下多元假设检验问题:

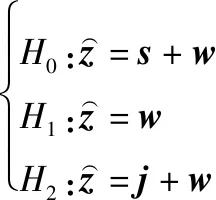
(27)

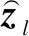
根据筛选出的样本构建干扰加噪声协方差矩阵为

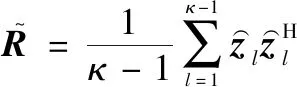
(28)

2.4 距离-角度二维自适应波束形成

最后,利用二维自适应波束形成实现干扰抑制。首先构造最小方差无失真响应(minimum variance distortionless response,MVDR)滤波器,即

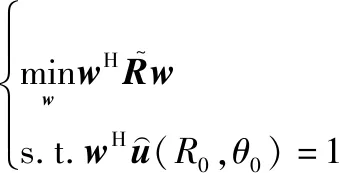
(29)

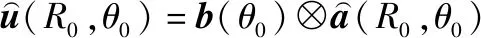
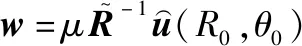
(30)

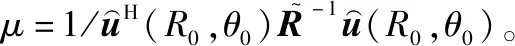
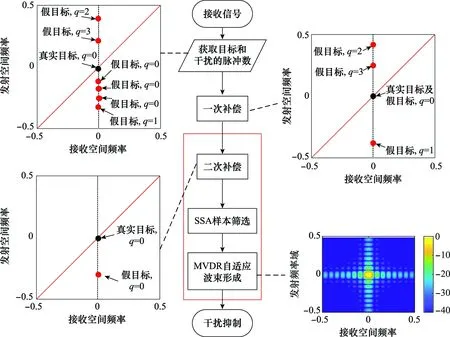
图3 基于时延差异二次补偿的主瓣距离欺骗式干扰抑制流程图Fig.3 Flow chart of mainlobe distance deception jammer suppression based on time delay difference with secondary compensation

3 抗干扰的效能评估

本节从能量、抑制率、信息熵3个方面对FDA-MIMO雷达抗干扰效能进行评估。

(1) 输出信干噪比(signal to interference plus noise ratio, SINR):

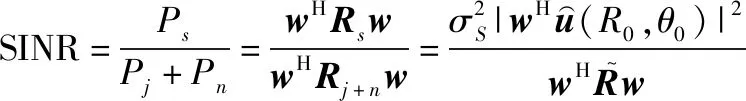
(31)

(2) 有源欺骗干扰抑制率

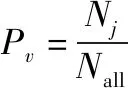
(32)

式中：表示被抑制掉的假目标数;表示有源欺骗干扰产生的假目标总数。该指标可反映已被抑制的假目标占比。

(3) 干扰信号熵

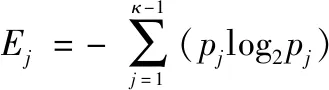
(33)

式中：表示干扰信号出现概率。该指标反映干扰信号的信息混乱度,混乱度越低,抗干扰效果越好。

4 仿真与分析

本节对抗干扰性能进行仿真分析。仿真参数如表1所示,其中包含干噪比(jammer to noise ratio, JNR)。假设自卫式干扰机产生了4个假目标,真实目标角度为0°,干扰均来自主瓣。其中,目标处于第300个距离门,4个假目标分别位于第310、200、368、334号距离门。其中,假目标1的距离模糊数与真实目标相同,假目标2、假目标3、假目标4相对于真实目标分别延迟了2、2、3个发射脉冲。

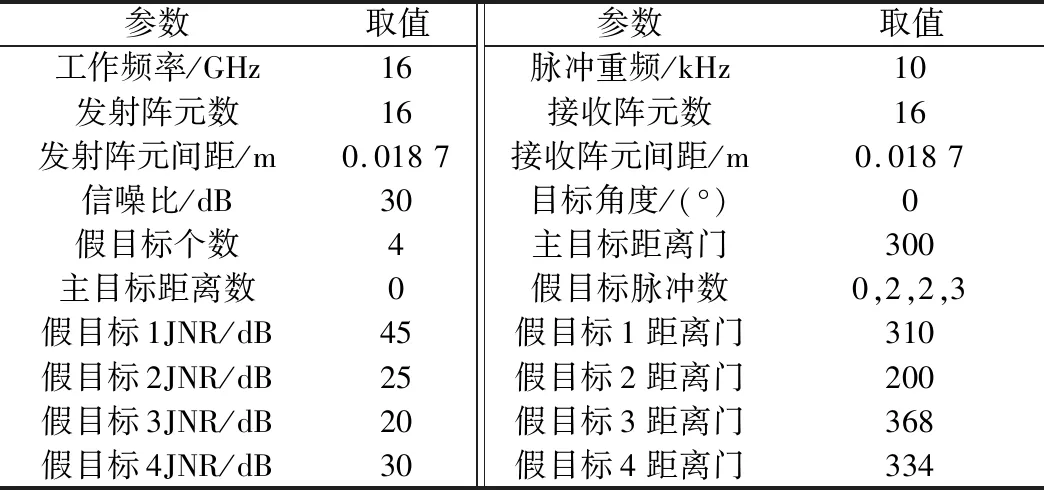
表1 雷达仿真参数Table 1 Simulation parameters of radar system

图4为未进行抗干扰处理的接收数据输出。如图3所示,进行CFAR检测后出现了多个假目标,即虚警,且真实目标无法被检测出来,出现漏警。

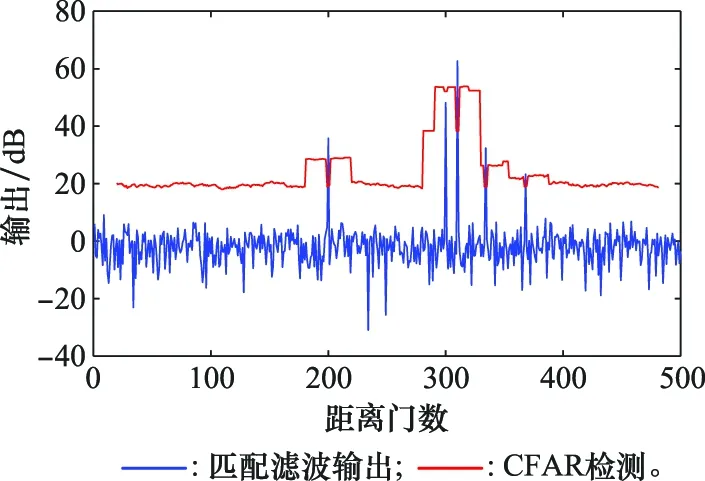
图4 未经抗干扰信号输出 Fig.4 Signal output without anti-jamming

图5给出了经过二次补偿前后的FDA-MIMO雷达收发二维功率谱。未补偿前,真、假目标接收空间频率保持一致,而发射频率有差异。经过一次补偿后,真、假目标在发射频率域上依据脉冲数聚集,即来自相同发射脉冲的假目标1和真目标聚集在同一点,来自相同距离模糊区的假目标2和3聚焦在同一点。经过二次补偿后,假目标1在发射空间频率上进行了平移,使得与来自于相同发射脉冲的真实目标发射空域上可分辨。此时,真实目标与假目标均可在收发二维空域上进行区分。

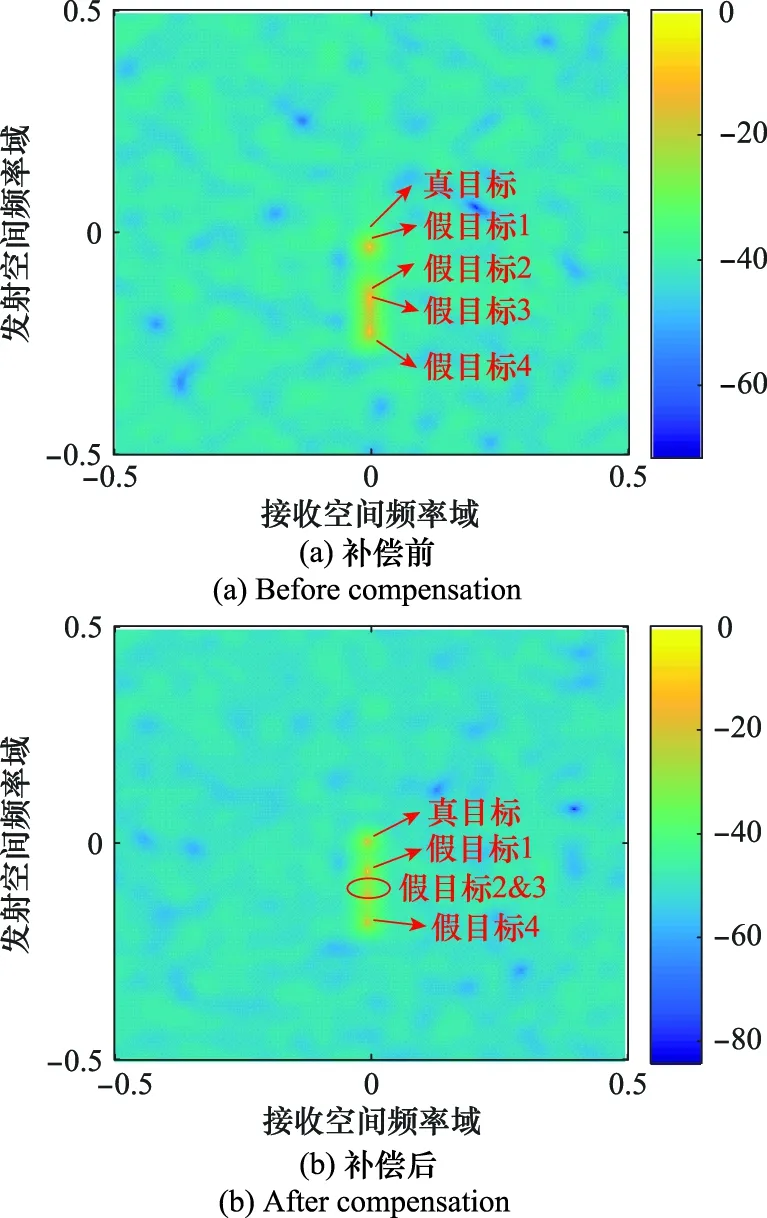
图5 FDA-MIMO雷达功率谱Fig.5 Power spectrum of FDA-MIMO radar

图6给出了一次补偿后和二次补偿后的波束形成方向图。如图6(a)所示,一次补偿后,由于仍存在脉内主瓣干扰,所以在主瓣方向有较大的零陷,产生了方向图畸变。如图6(b)所示,经过二次补偿及自适应波束形成后,脉内快速转发的主瓣干扰由于距离维失配而被抑制,因此方向图在真实目标处响应最大。

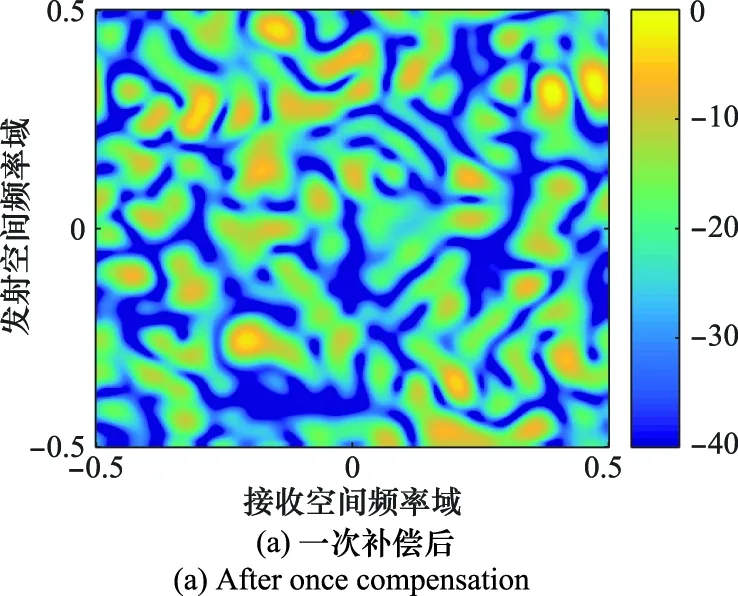
图6 FDA-MIMO雷达自适应波束形成方向图Fig.6 Adaptive beampattern of the FDA-MIMO radar

图7为经过一次补偿后和二次补偿后的自适应滤波输出。由于一次补偿并不能分离假目标1和真目标,所以仍然存在干扰剩余。目标无法通过CFAR检测到,目标的输出功率很低，如图7(a)所示。然而,经过二次补偿,目标和假目标1能够被有效分离,且利用自适应波束形成可以有效抑制假目标1,只有真实目标被检测出,且具有最大的输出功率，如图7(b)所示。

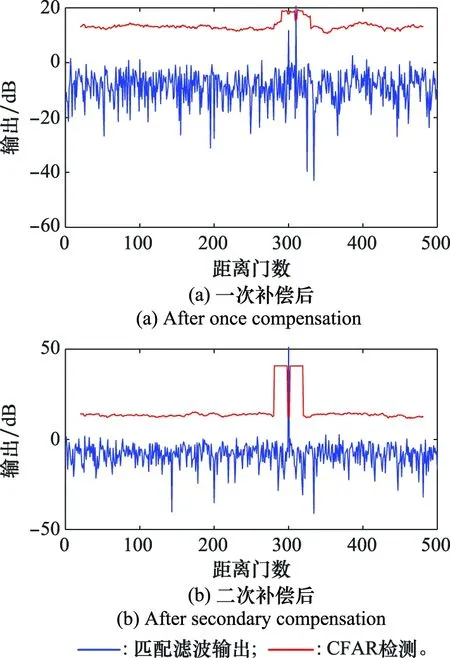
图7 自适应滤波输出Fig.7 Adaptive filter output

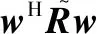
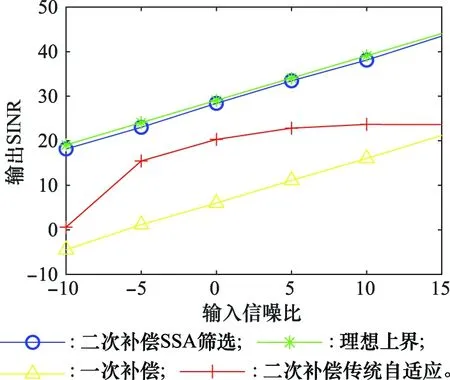
图8 不同方法的输出SINR对比Fig.8 Comparison of output SINR in different methods

此外,一次补偿后干扰抑制率=75%,经过二次补偿以及自适应波束形成后上升至100%,有效对所有假目标进行了抑制。干扰信号的熵值未补偿前为6.5,一次补偿后为0.257 5,二次补偿后为0,故抗干扰效果较好。

5 结 论

本文提出一种基于二次补偿的FDA-MIMO雷达主瓣欺骗式干扰抑制方法。首先依据延迟脉冲数差异和脉内距离差异构造补偿矢量,在发射空域上对真实目标和假目标进行区分,再使用SSA方法筛选奇异样本并剔除真实目标样本,从而获取准确的干扰噪声协方差矩阵,最后利用自适应波束形成滤波器对距离维失配的干扰进行抑制。

未来将针对FDA-MIMO多目标情况下的抗干扰以及灵巧干扰抑制问题开展研究,进一步提升FDA-MIMO 雷达抗主瓣欺骗式干扰的能力。