长空气间隙50%放电电压的测量不确定度分析

李恩文，李斌，蒲金雨，刘磊，黄欢，黎小林，唐力

(1. 特高压电子技术与新型电工装备基础国家工程研究中心(南方电网科学研究院)，广州510663；2. 贵州电网有限责任公司电力科学研究院，贵阳550002)

0 引言

长空气间隙的操作冲击放电特性是输电工程线路和换流站/变电站空气间隙选择的重要依据之一。每一种新的空气间隙结构的设计与选择，均需在试验基地进行大量的真型试验，获取间隙上放电的概率为50%的电压值U50，将试验结果进行海拔矫正，并乘以一定的安全系数，再应用于工程实践[1 - 3]。

近年来，国内外研究人员对长间隙放电机理研究不断深入，为气体放电过程的计算逐步奠定了基础[4 - 8]。学者们建立了多种放电电压计算模型，用于计算长空气间隙的放电电压，并将空气间隙放电电压的计算值与试验值进行对比，以验证所建立计算模型的有效性[9 - 15]。在文献[9]中，对于750 kV不同杆结构，50%放电电压U50计算值和试验值的平均偏差为2.45%，对于1 000 kV不同杆塔结构，偏差为3.02%。文献[10]中带电作业组合间隙50%放电电压计算值和试验值的平均偏差不超过6%。文献[11]中对于均压环与直流杆塔塔头空气间隙的放电电压，计算值和试验值的平均偏差为3.7%。文献[12]中酒杯塔边相空气间隙放电电压计算值和试验值的平均偏差为3.66%。

实际上，对于某一长度的间隙，试验值自身也存在误差。在上述文献的模型验证过程中，通常将试验值当做“客观真实值”来对模型的有效性进行验证，通常忽略了试验值本身的误差。在特定的环境条件下，间隙的50%放电电压是一个客观存在的物理值，做试验的过程即为对该客观物理值进行测量的过程。由于试验设备的精度是有限的，试验得到的测量结果必然与间隙客观存在的50%放电电压物理值之间存在误差[16]。此外，50%放电电压并非是间隙长度的单一函数，除间隙长度外，放电电压值还受空气密度(海拔)、温度、湿度、光照等多重因素的影响。再加上试验过程中环境变量的变化，试验结果与客观真实值之间的误差被进一步放大[17 - 19]。因此，在高压试验工作，尤其是对于长空气间隙的操作冲击电压试验，即使是对于完全相同布置的试品间隙，在不同时段进行重复试验的时候，试验结果的差异也会达到几十千伏。将试验结果进行海拔矫正时，由于现有的海拔矫正方法还不够完备，海拔矫正过程也会引入数据不确定度。本文研究在换流站阀塔均压罩对地间隙放电试验中，就曾遇到一个比较典型的与海拔矫正引入试验数据不确定度相关的例子：在相邻的两天对不同长度空气间隙用升降法测量U50，并根据项目研究的需要，将试验数据利用g参数法海拔矫正到标准气象条件下。海拔矫正前，试验结果为3.5 m间隙的U50为1 348.5 kV，4 m间隙的U50为1 418.0 kV。但利用g参数法将上述试验结果矫正到标准气象条件下时，得到的结果却为3.5 m间隙的U50为1 785.4 kV，4 m间隙的U50为1 684.8 kV，长间隙的U50反而比短间隙值小。经检查分析是试验数据有误差，该误差在海拔矫正中传递和放大，并最终呈现出标准气象条件下同一间隙类型工况。长间隙的U50反而比短间隙值小的结果如表1所示。

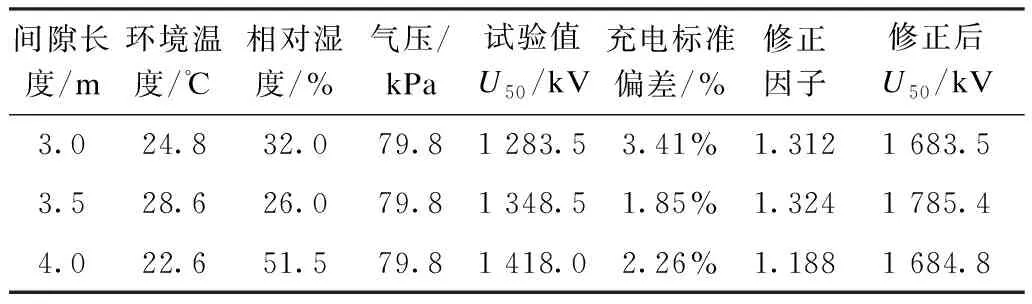
表1 试验数据及海拔矫正结果Tab.1 Test data and altitude correction results

随着试验能力和测量技术的提高，对气体放电过程的观测愈加微观，气体放电的计算模型也愈加精细，利用应用数学和计算机科学解决或解释长间隙放电问题的研究将越来越丰富，对试验结果的准确度必然提出更高要求。基于上述分析，对试验数据的质量进行定量评估很有必要。但目前对长空气间隙放电试验结果准确度的研究还比较少，环境温度对试验结果的影响往往是定性的概念，缺乏定量说明。本文对此开展研究，构建了一个用于评价“升降法”测量U50的试验结果不确定度的计算方法，以阀塔均压罩对地构成的长间隙放电试验为例，参照国家标准《GB/T 27418—2017测量不确定度评定和表示》[20]及数理统计的相关方法[21 - 23]，对长空气间隙击穿电压试验的准确度进行详细分析，为长空气间隙试验以及基于试验值的仿真分析等研究提供参考。

1 U50的测量不确定度

1.1 不确定度的相关理论

不确定度与误差都用于刻画测量结果的质量，只是误差是一个理想概念不可能准确获知，不确定度是利用可获得的信息得到的表征被测量量值分散性的非负参数[20]。当报告物理量的测量结果时，通常需要对测量结果的可靠程度进行定量说明，得到的测量值只是被测量值的近似值或者估计值。对试验结果(估计值)有不确定度声明时，它才是完整的试验结果。长空气间隙的放电试验结果也是如此，有必要对其可靠程度进行定量说明。

从影响结果的因素考虑，测量结果的不确定度一般来源于被测对象、测量设备、测量环境、测量方法和测量人员。不确定度通常用测量量估计值的标准差表示。

很多情况下，测量量Y不能直接测得，而是由N个其他量X1,X2,…,XN通过函数关系f来确定。

Y=f(X1,X2,…,XN)

(1)

式中XN为输入量，也可能是被测量。XN的值取决于其他量，从而导致一个复杂的函数关系，以至函数f不能明确地表示出来，是一个广义的函数。被测量Y的测量结果(即估计值)用y表示，则y的标准不确定度uc(y)由输入量的估计值x1,x2,…,xN的标准不确定度合成得到：

(2)

式中：合成标准不确定度uc(y)为y的估计标准偏差，表征可合理赋予被测量Y的值的分散性；u(xi)表示输入量Xi的估计值xi的标准不确定度；灵敏系数ci=∂f/∂xi是在Xi=xi时∂f/∂Xi的值，用于描述不确定度随输入量x1,x2,…,xN传递到输出量的估计值y的传递系数。式(2)表示不确定度的传播规律。

每个输入量估计值xi的标准不确定度u(xi)是由输入量Xi可能值的分布获得的，可能是根据Xi的n次独立重复观测值序列{Xik}得到的频率分布，或者是一种先验分布。

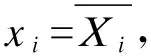
(3)

式中s(Xi)为序列{Xik}的标准差。该情况下u(xi)是通过重复观测统计得到的，称为A类不确定度，它的自由度为vi=n-1。

当输入量Xi的估计值xi不能由重复观测得到，u(xi)可根据Xi可能变化的全部有关信息来判断评定，信息来源通常包括：1)生产厂商提供的技术说明书；2)校准证书或其他证书提供的数据；3)取自相关试验手册或者标准、规范书赋予的参考数据的不确定度；4)对有关材料和仪器特性的经验。这一类评定称为u(xi)的B类标准不确定度，其自由度为：

(4)

测量量Y的自由度veff由韦尔奇-萨特思韦特公式得到：

(5)

式中ci=∂f/∂xi为灵敏度系数。

不确定度分析确定一个合理的区间y±Up， 该区间包含了合理表征Y分布特性的置信水平p，其中，Up=uc(y)kp，kp由概率p和Y的自由度veff决定，通过查询t分布表得到。

1.2 U50的不确定度分析

1.2.1 分析流程

空气间隙50%放电电压不能直接测得，而是采用多次试验，利用统计的方法间接近似求取。根据文献[2]，试验方法包括“多级法”、“升降法”和“连续放电”3类试验。其中“升降法”试验工作量较小，具有方便快捷的特点，被广泛应用。用升降法试验前，先预估空气间隙的50%放电电压U50，选取一个接近U50的数值作为初始电压施加在空气间隙上。如果空气间隙在本次施加的电压下放电击穿，则下一次加压时电压减小ΔU； 如果本次加压未发生放电击穿(耐受)，则下一次加压时电压增加ΔU。 电压极差ΔU约为U50估算值的1.5%～3%。重复上述过程，使得有效加压次数n在20次以上。记录每次施加电压的数值，利用统计的方法由式(6)近似求取U50[2]。

(6)

式中：n为升降法试验中的加压次数；Ui为第i次施加的电压值。

U50虽然是一个统计值，但它反映的是在特定环境条件下空气间隙的物理击穿特性，在固定气压、温湿度、间隙长度条件下是一个客观存在的值。在环境条件固定不变的理想情况下，倘若对间隙施加无数次的该客观真值电压U50，间隙的击穿和耐受次数应各占50%。利用“升降法”获取U50的过程就是对该客观存在的真值进行“测量”的过程。

由于“测量”过程中受各种因素的影响，U50的“测量值”与客观真值之间总是存在偏差，由于客观真值无法知道，该偏差只能根据该测量过程的相关规律进行评估，即测量结果不确定度分析。该过程的总体思路是将可能导致测量结果出现偏差的各种因素都纳入考虑，逐一估算各个因素导致的测量结果偏差的大小，再将各种因素的影响合成得到最终结果。

U50试验结果的不确定度主要来源于试验方法、试验设备等6个方面，如图1所示。其中试验方法引入的不确定度为：在试验过程中，有限次试验次数和施加电压的极差所导致的不确定度，倘若试验次数无穷大，施加电压的极差无穷小，则该不确定度也将趋近于无穷小。试验方法引入的不确定度利用参数估计方法进行评估。分压器和充电电压控制系统精度有限，也会引入不确定度，利用相应的校准证书和测量仪器的准确度等级进行评定。试验过程中，试品摆动导致间隙距离变化也会导致试验结果不准确，该因素利用前期试验规律进行评定。此外试验过程中温湿度的变化也会引入不确定度，利用g参数法中的大气修正因子对其进行评定。

图1 U50不确定度分析流程Fig.1 Analysis process of U50 uncertainty

先逐一分析各个因素的标准不确定度分量；再利用方差合成的方法得到合成标准不确定度uc，最后乘以相应置信水平p的包含因子kp即得到扩展不确定度Up为：

Up=kp·uc

(7)

另外试验在户外试验场开展，光照、风速等因素对放电电压也有一定的影响，但是暂无法进行定量分析，风速光照为随机因素，近似认为对试验结果的不确定度影响通过式(6)计算之后可忽略。

1.2.2 参数估计方法

(8)

(9)

表2 参数G的典型值Tab.2 Typical value of parameter G

1.2.3 大气修正因子

空气间隙击穿电压与试验时的大气条件有关，通常放电电压随着空气密度或湿度的增加而升高，放电电压值正比于大气修正因素Kt[2]，具体为：

Kt=k1k2

(10)

k1=δm

(11)

k2=kw

(12)

(13)

(14)

(15)

式中：k1为空气密度修正因素；k2为湿度修正因素；δ为相对空气密度；k为取决于绝对湿度h与相对空气密度δ的比率h/δ的函数；L为最小放电路径，m；U50为试验电压值，kV；指数m和w由g的取值范围得到[2]；h为绝对湿度，g/m3；R为相对湿度，用百分数表示；t为环境温度，℃；t0和q0为标准参考大气条件，t0=20 ℃，q0=101.3 kPa；q为大气压强。

2 均压罩对地间隙的U50不确定度评定

在昆明特高压试验基地(海拔2 100 m)对由换流阀均压罩与大地组成的空气间隙进行操作冲击放电试验，间隙距离为7 m，利用升降法测量其50%放电电压U50，一共施加电压30次，每施加5次电压，测量一次温湿度。试验照片如图2所示，试验结果如表3所示。冲击电压发生器的标称电压为7 200 kV，一共有36级，每一级充电电压上限为200 kV。在本次试验中，单级充电电压在69～72 kV之间，充电极差为1 kV。

图2 阀塔均压罩的操作冲击放电试验Fig.2 Operational impulse discharge test of grading shield

由表3计算所得，该间隙的50%放电电压为1 716 kV，测试时的环境平均湿度为38.4%，平均温度为26.7 ℃。

2.1 不确定度分量分析

2.1.1 试验方法引入的不确定度u1

试验的统计参数i、ni、mi如表4所示。在该次试验中，击穿次数N=15，耐受次数M=15，各个参数的值为A1=18，B1=30，A0=3，B0=9。

冲击发生有36级，充电电压的极差为1 kV，充电效率为67.4%，因此施加到空气间隙上的电压极差ΔU为24.26 kV。利用式(8)计算可得：

表3 试验数据Tab.3 Test data

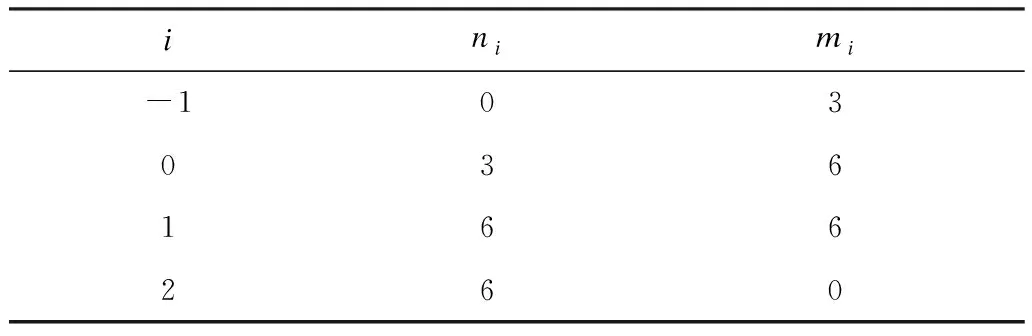
表4 统计参数Tab.4 Statistical parameters of test data

根据表2可得，G=1，利用式(9)计算得：

不确定度u1为：

有效自由度为：

veff(u1)=n-1=29

2.1.2 分压器引入的不确定度u2

经国家高压计量站校准，该高压发生器测量系统分压比的扩展不确定度为1.9×10-2，包含因子为k=2，估计其可靠度为10%，则由测量系统引入的标准不确定度为：

veff(u2)=(1/2)(10/100)-2=50

2.1.3 间隙测量引入的不确定度u3

本次试验的空气间隙为7 m，但是由于阀塔均压罩体积较大，在试验过程中会随风摆动，其对地距离也会有所变化u(L)为0.03 m。根据前期的试验数据，在7 m间隙附近，放电电压与距离的函数关系近似为：

U=117.22L+923

所以，距离d引入的标准不确定度为：

估计u(L)的可靠性为25%，自由度为：

veff(u2)=(1/2)×(25/100)-2=8

2.1.4 温度变化引入的不确定度u4

该次试验历时40 min，共测量了7次，试验中的温度数据如表3所示。其平均温度为26.7 ℃。温度的A类不确定度为：

veff(ut1)=7-1=6

温度计校准证书显示，在0～40 ℃范围内温度计的误差范围为±1 ℃，所以温度的B类不确定度为：

校准证书给的是温度计的上下限，因此认为veff(ut2)=∞。

温度的不确定度ut为：

veff(ut)=veff(ut1)=6

利用海拔矫正方法中的大气修正因子分析温度变化对放电电压的不确定度传递，该过程涉及参数较多，逐一分析如下。

1)绝对湿度h

由绝对湿度与温度的函数关系式(15)得到温度不确定度传递系数为：

因此，温度导致的绝对湿度的不确定度为：

2)相对空气密度δ

由空气密度与温度的函数关系式(13)得到温度不确定度传递系数为：

因此，温度导致的相对空气密度变化的不确定度为：

3)参数k

参数k的函数表达式为：

不确定度传递系数为：

因此，k的不确定度为：

4)参数g

由参数g的函数表达式(14)得不确定度传递系数为：

因此，g的不确定度为：

5)参数m的不确定度

参数m的函数表达式为：

m=g(g-0.2)/0.8

不确定度传递系数为：

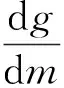
因此，m的不确定度为：

6)参数w的不确定度

参数w与m的函数表达式相同，其不确定度为：

u(wt)=u(mt)=0.004 2

7)大气修正因素K的不确定度

根据参数K的函数表达式(10)，不确定度传递系数为：

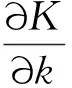
大气修正因素K的不确定度为：

8)温度的变化导致的U50的不确定度

根据大气修正公式U50=U0K， 略去高阶项，参数K不确定度传递系数为：

(16)

温度变化引入的U50的不确定度为：

u4=U0u(Kt)=3.72 kV

veff(u4)=veff(ut)=6

2.1.5 相对湿度变化引入的不确定度u5

湿度的A类不确定度为：

veff(uR1)=7-1=6

湿度计校准证书显示，湿度计的误差范围为±5%，所以湿度的B类不确定度为：

校准证书给的是温度计的上下限，因此认为：

veff(uR2)=∞

湿度的不确定度uR为：

veff(uR)=veff(uR1)=6

利用g参数法，通过与上述分析温度引入的不确定度u4类似的计算分析方法，得到：

1)参数w与m的不确定度为：

u(wR)=u(mR)=0.004 8

2)参数k的不确定度为：

3)参数K的不确定度传递系数为：

大气修正因素K的不确定度为：

4)相对湿度的变化导致的U50的不确定度

根据式(16)，湿度变化引入的不确定度为：

u5=U0u(KR)=5.59 kV

veff(u5)=veff(uR)=6

2.1.6 充电电压引入的不确定度u6

该冲击电压试验系统的验收资料表明，该系统的单次充电电压整定偏差ai≤±1%， 估计其可靠度为10%。在试验中，单次充电引入的标准不确定度为：

则由充电电压引入的标准不确定度为：

veff(u6)=(1/2)(10/100)-2=50

各个分量的标准不确定度如表5所示。

2.2 扩展不确定度

间隙50%放电电压U50的合成标准不确定度为：

有效自由度为：

通过查t分布表可知，自由度为80，置信度为95%的包含因子为：

kp=tp(veff)=t0.95(80)=1.994

该次试验的扩展不确定度为：

Up=kp·uc=38.1 kV

因此，本次试验的结果完整表述为：在环境湿度为38.4%，温度为26.7 ℃，海拔2 100 m时，7 m长的均压罩对地间隙的50%放电电压为1 716 kV；其扩展不确定度Up=38.1 kV， 占比为2.2%，按置信水准p=95%， 自由度v=80所得t分布临界值对应的包含因子kp=1.994而得，即：间隙的U50有95%的概率处于区间(1 716 kV±38.1 kV)内。

2.3 结果分析

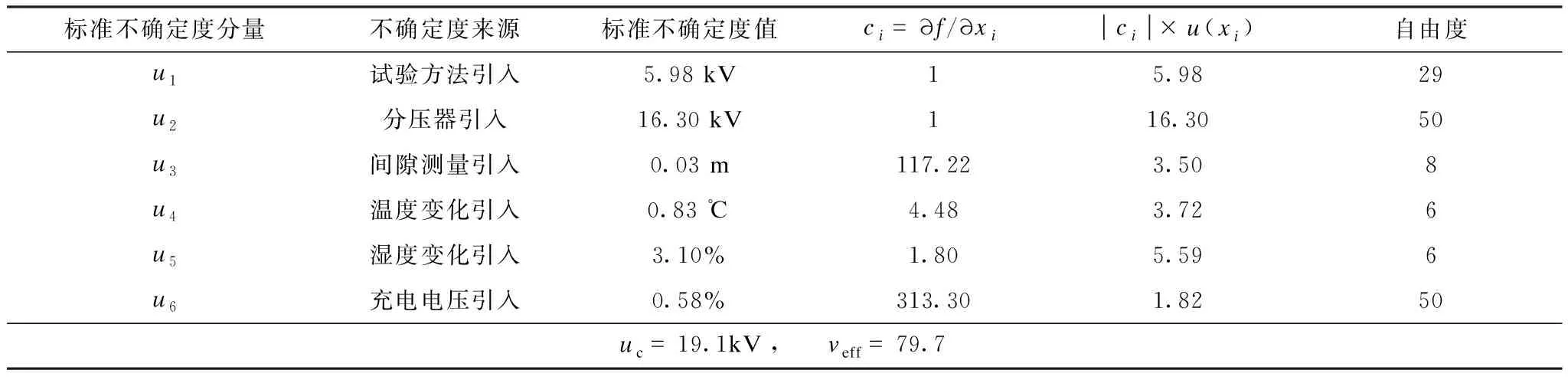
表5 标准不确定度一览表Tab.5 List of standard uncertainty components

在某一固定的气压、温度和湿度条件下，空气间隙的击穿特性是固定的，50%放电电压也是某一个具体的客观数值，但是无法直接测量该数值，无法准确地获取空气间隙的击穿电压分布，只能通过“多级法”、“升降法”等试验方法间接的进行测量。在间接测量过程中，又有诸多因素会导致测量结果不准确，包括试验方法引入的偏差、高压分压器测量引入的偏差、试验过程中环境温湿度的变化引入的偏差等，这些因素综合作用最终导致测量得到的50%放电电压结果存在误差，只能通过计算分析一定概率地确定U50所处的区间范围。

导致U50测量结果不准确的各个因素，只能对其进行控制，以减小其引入的不确定度，但无法消除。由表5可知，在该次试验中，分压器测量引入的标准不确定度分量最大，为16.3 kV。经国家高压计量站校准，该高压发生器测量系统分压比的扩展不确定度为1.9%(标准GB/T 19627.2—2011要求小于等于3%[25])，如果能进一步提高分压器的准确度，则能有效降低测量结果的不确定度。

试验方法引入的标准不确定度分量仅次于分压器，试验结果为5.98 kV。从式(8)—(9)可以看出，较小的充电极差和较大的试验次数能减小试验方法引入的不确定度。但在实际试验中，若无限制地减小充电极差和扩大试验次数，会导致试验时间过长，环境温湿度变动过大，引起测试结果不确定度增大。

此外，空气间隙测量、试验过程中环境温湿度的变化等因素都会导致结果不准确，测试不确定度增加。尤其值得注意的是，间隙长度引入的不确定度的传递系数较大，试验结果为117.22，对测试结果的影响较大。该次试验在户外场进行，将均压罩吊起来形成对地间隙开展试验，由于均压罩体型较大，在试验中会因风吹导致轻微的摆动，进而导致对地间隙无法准确的控制为所需要的7 m，估算间隙的变化为3 cm。由于传递系数较大，3 cm的距离变化将引入3.5 kV的标准不确定度分量。

温度和湿度是具有一定的负相关性的，在合成标准不确定度时，可引入温湿度的协方差估计值，确定二者的相关系数，再结合各自的灵敏度系数计算二者的相互作用对U50试验结果的影响大小。在用“升降法”测试U50的实验中，温度和湿度的变化相对较小，例如本文中温度标准不确定度为0.83 ℃，0.83 ℃的温度偏差导致相对湿度的变化，进而间接导致的试验结果的偏差比较小，因此本文中忽略温、湿度的相互作用。

温、湿度的变化引入的不确定度分量分别为3.72 kV和5.59 kV，将两者进行合成，并乘上扩展因子2，可得二者的扩展不确定度为13.4 kV，占测试结果1 716 kV的0.78%。温、湿度的变化对间隙击穿电压有显著影响，在该次试验过程中时间不长，温、湿度变化不大，就已经对结果引入了0.78%的不确定度。如若是在一年中不同时节开展试验，温湿度有较大变化，例如温度变化10 ℃，湿度变化20%，按照表5中的传递系数，测试结果的扩展不确定度将高达115 kV，占1 716 kV的6.7%。现有的放电电压计算模型研究，主要从电极形式及电场分布等角度出发进行分析计算，对温湿度的影响考虑较少，若能将温湿度的影响进行建模分析，有望进一步提升计算模型的有效性。

3 结论

本文建立了“升降法”测量长空气间隙50%放电电压的测量不确定度分析方法，以换流阀均压罩对地间隙试验为例，分析了试验结果不确定度的各影响因素来源，各分量不确定度的大小，并对计算结果进行讨论，得到如下结论。

1)影响试验值不确定度的因素较多，试验方法、试验过程中的环境因素变化等都会引入不确定度，导致试验结果与客观真值存在偏差。进行高压试验时，有必要对试验结果的不确定度进行分析，对试验结果的好坏给出定量的说明，以便于试验结果被更为科学合理地利用。不同影响因素中，高压发生器测量系统引入的不确定度较大。提高高压发生器的测量、控制精度，适当减小“升降法”的加压极差，能有效减小50%放电电压的测量不确定度。

2)“升降法”试验值的不确定度有百分之几的占比，本文计算结果为2.2%，同现有长空气间隙的放电电压计算模型的计算结果偏差处于同一数量级。在放电电压计算模型有效性验证中，有必要将试验值本身的不确定度纳入考虑，对各种因素对间隙结构放电特性的影响进行更加细致的研究，提升放电电压计算模型的有效性。

3)在本文的试验案例中，温度的不确定度传递系数为4.48，湿度的不确定度传递系数为1.8，温度对试验结果的影响更为显著。在将试验基地的试验结果用于工程实践时，可根据工程实际地点的温、湿度变化范围，和该间隙温、湿度的不确定度传递系数，确定U50的概率分布区间，为生产建设提供参考。

本文借用误差传递的分析方法对空气间隙50%放电电压的测量不确定度进行了初步的探讨分析，但是长空气间隙放电是一个多因素综合影响的复杂过程，各种因素之间的相互作用对试验结果的影响有待进一步研究。由于试验条件的限制，尚未对本文的计算结果进行试验验证。同时，海拔校正是将试验结果应用于现场生产的重要环节，该环节引入的不确定度的评估也有待开展。