基于ADAMS的烟包裹包凸轮连杆机构动力学分析

葛正浩，王英杰，王少华，赵秋节

（陕西科技大学 机电工程学院，西安 710021）

0 引言

凸轮连杆机构由于间歇运动精度高，定位准确以及结构紧凑而被广泛应用于自动机械中，例如分拣、包装、食品、制药、烟草等领域，以代替繁杂的人工操作，提高生产效率[1]。烟包裹包凸轮连杆机构作为烟草机械中驱动装置和传动装置，因其可实现多样化的运动规律和稳定的运行状态，一直被该领域所青睐。近年来在一些新兴领域也开始应用，贾毕清结合我国现有蔬菜生产情况,依据串联式凸轮-连杆组合机构的设计方法，设计了一种可完成垂直取苗、自动投苗的取苗机构[2]。刘龙通过对凸轮连杆机构的研究，对高速印刷机机构的设计进行了说明[3]。谢祖清基于凸轮-连杆组合机构的稳定传动特性设计了一种由其驱动的双足机器人[4]。文献[5]在步态康复机器人的概念设计中，以两自由度的七杆曲柄滑块机构为原型，设计了一种凸轮连杆机构。文献[6]为了解决停车难的问题，设计了一种新型的凸轮联动的双平行四边形机构，通过动态静力学分析证明了双平行四边形机制的优点以及该停车系统的可行性。

刚柔耦合动态分析是目前较为常见的机构动力学分析方法，它可以避免刚性系统与实际情况不符和柔性系统求解难度大的缺陷。因此，本文综合考虑烟包裹包凸轮连杆机构实际工况，对其进行了全刚性的动力学仿真分析后，将刚性凸轮安装轴替换为柔性轴，建立了刚柔耦合虚拟样机，进行仿真分析，通过对比替换前后运动曲线的特征，提出机构改进措施。

1 压烟机构运动学分析

1.1 压烟机构坐标系建立

以凸轮回转中心为原点，压烟板的回退方向为Y轴正向，建立机构坐标系。

将各杆长表示为li，各杆角位移对应为θi；C01和CD夹角为β，FE和FG夹角为γ。设在初始位置时H点与F点之间在Y轴投影的距离为YFH，在X轴投影的距离为XFH。

机构自由度数等于原动件数，运动确定。

1.2 运动学建模与求解

按串联型凸轮连杆机构模块化设计思想将压烟机构划分为对应的三个模块，应用闭环矢量法分别得到三个模块方程组：

1）角位移的求解

对其矢量投影后，可得：

式(3)中：l1至l8，θ2，θ5，θ6均已知；

XDF—铰链D和F之间的水平距离；

r—滚子半径；

θ—凸轮转角；

l(θ)—OP的长度，即随压烟凸轮转角θ变化的凸轮当量半径。

结合杆件位置关系和式(3)得出机构中各个构件的角位移和滑块的线位移方程：

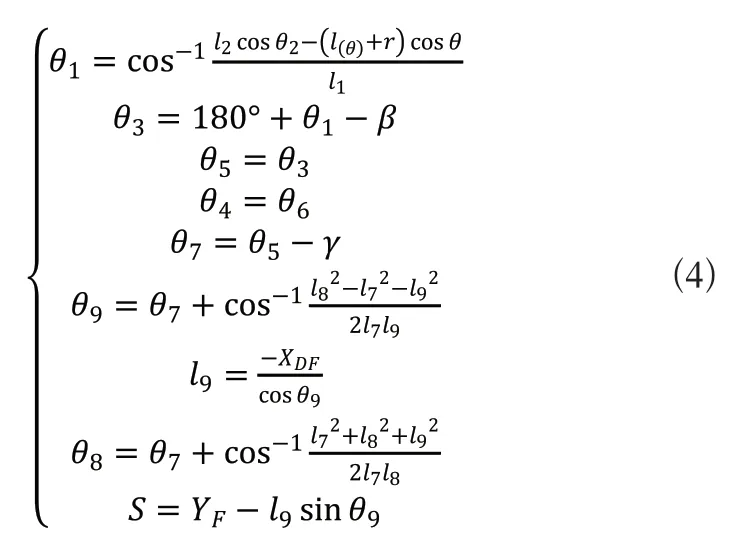
可见只要给定θ和l(θ)后，其它角位移皆可求出，下面给出凸轮的当量半径l(θ)的算法。

如图3所示，设机构摆杆摆角为ψ，O点为凸轮旋转中心，P点为凸轮与滚子接触点，则OP为压烟凸轮的当量半径l(θ)[7]，已确定的参数还有：滚子半径r、中心距l2和滚子摆杆AQ的长度l1。

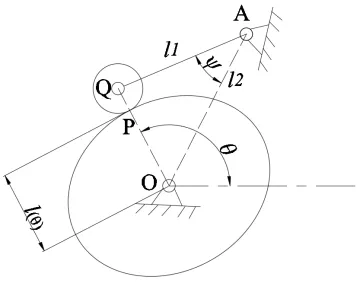
图3 凸轮机构简图

在三角形OAQ中，根据余弦定理可得：

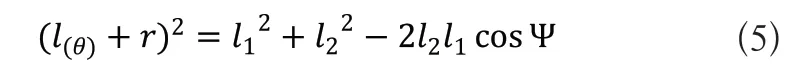
借助摆杆的运动规律可求得机构运动过程中摆杆摆角的变化情况：

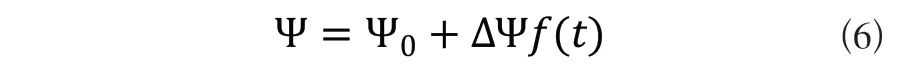
式(6)中：

ψ0—摆杆的初始摆角（rad）；

Δψ—摆杆的总摆动角度（rad）；

f(t)—摆杆的凸轮曲线规律。

将式(6)代入式(5)，得到在凸轮机构运动过程中的凸轮当量半径的变化函数：

近年来，随着高校基础设施的完善和投入的持续增加，我国高校场馆设施逐步增多，开放率有较大提高。“六普”统计数据显示，2013年高等院校体育场地对外开放情况为：不开放场馆设施数为27 393个，占比55.06%；部分时段开放10 294个，占比20.69%；全天开放场馆设施数为12 063个，占比24.25%[7]。有将近一半左右的高校在满足日常体育教学需要的同时，选择对外开放场馆设施，为公众参与体育活动提供了较多高品质的健身场所，有效缓解了公众健身场地设施不足的困境，而高校场馆设施对外开放只是迈出了场馆高校利用的第一步，在未来还应继续探索多元化运营模式。

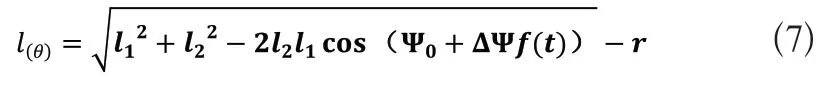
2）角速度的求解

图1 烟包裹包凸轮连杆机构三维模型

由图2杆件位置关系知：

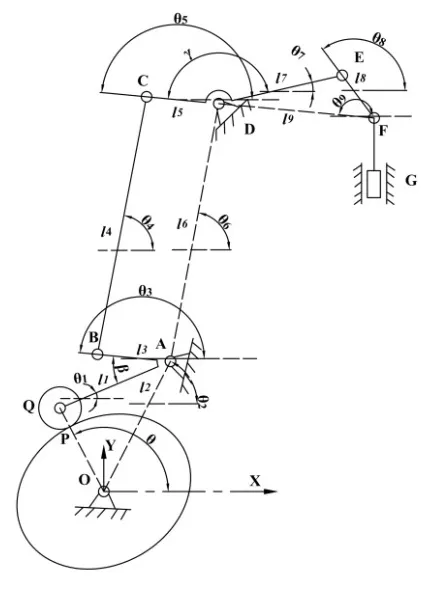
图2 压烟机构的坐标系

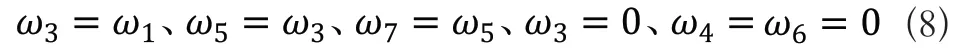
将式(3)对时间t求导，可求得各杆件的li角速度i和滑块速度v：

求解式(9)得：

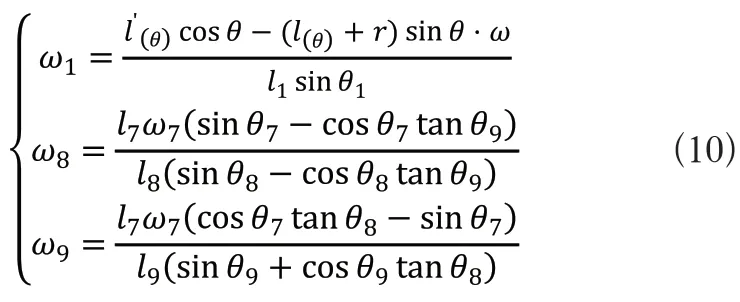
3）角加速度的求解

根据杆件位置关系得：

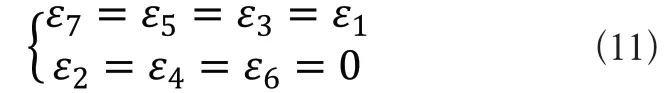
式(9)对时间t求导后，可得到各杆件li的含角加速度的和滑块加速度a的表达式：

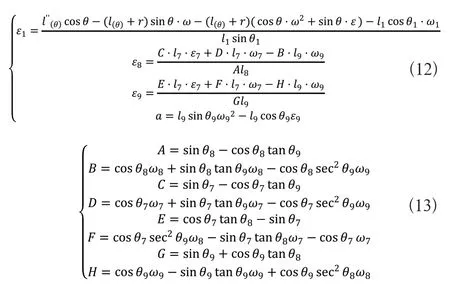
2 裹包凸轮机构多刚体动力学仿真分析

2.1 裹包凸轮机构多刚体动力学模型建立

将Creo中建立好的烟包裹包凸轮机构三维模型做合理简化后导入ADAMS中，对其进行各参数的设定，完成多刚体动力学模型的建立。

图4 裹包凸轮机构多刚体动力学模型

ADAMS通过内置函数来对碰撞进行定义，接触参数设定是其关键。

材料接触刚度计算如式(14)所示：

式(14)中：

μ1、μ2——凸轮和滚子各自的泊松比；

r1、r2——凸轮和滚子各自的当量半径（mm）；

e1、e2——凸轮和从动件滚子各自的杨氏弹性模量[8]（N/mm2）。

查阅材料特性值后可求得：

计算当量直径：

空心工件：D=L/π，L为不规则工件的周长；

实心工件：D=2(S/π)1/2，S为不规则工件的截面积[9]。

利用Creo的分析测量功能，根据测得的数据计算得到当量半径，代入式(14)可求得材料的接触刚度系数值K：

2.2 摆杆动态性能分析

在Creo中对凸轮机构在600r/min的转速下进行仿真，得到各摆杆的理论运动曲线，如图5～图7所示。

图5 压烟摆杆的理论运动学曲线

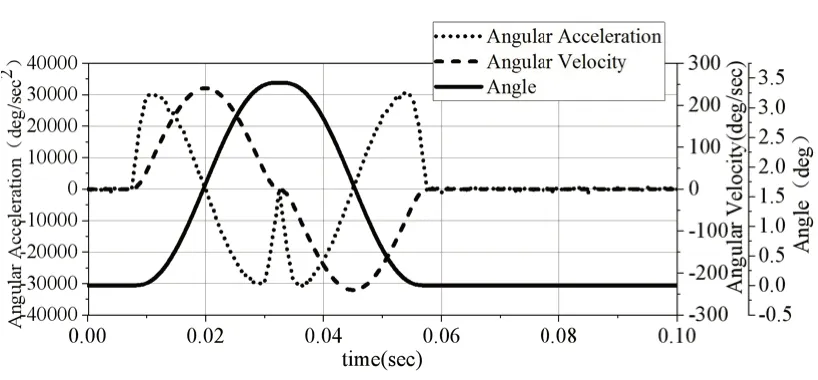
图6 预折叠摆杆的理论运动学曲线

图7 护烟摆杆的理论运动学曲线

在ADAMS中进行动力学仿真，设定凸轮轴转速为600r/min；得到动力学仿真曲线，如图8～图10所示。

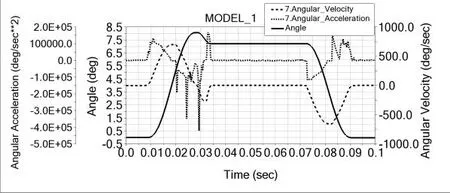
图8 压烟摆杆的角位移、速度和加速度曲线

图9 预折叠摆杆的角位移、速度和加速度曲

图10 护烟摆杆的角位移、速度和加速度曲线

图5～图7与图8～图10中各曲线分别对比后，发现各摆杆角位移曲线与其理论曲线一致，角速度曲线稍波动，而角加速度曲线变化趋势及幅值与理论值一致，验证了模型的准确性。同时角加速度出现抖动与冲击，一是由于通过取有限点拟合法生成凸轮轮廓曲线，拉伸出的凸轮曲面不是绝对地光滑；二是由于所给定转速太快，所产生的惯性冲击会更大；三是由于修正正弦运动规律横越冲击不可避免。

3 裹包凸轮机构刚柔耦合动力学仿真分析

3.1 刚柔耦合虚拟样机的建立

高速凸轮机构由于其轮廓曲线数据随凸轮曲线的周期性变化、惯性冲击和凸轮与滚子的接触碰撞都将导致元件的弹性变形，产生振动。因而其主要零件的柔性变形不可忽略，故应对机构主要弹性变形构件进行柔性化处理，使所得仿真结果更加接近实际工况[10，11]。

烟包裹包凸轮机构中的凸轮安装轴为3个凸轮的支撑部件，其除了承受凸轮的重力外还要受其惯性力和碰撞力的影响，尤其在高速运行期间其影响会成倍增加，并且凸轮安装轴的刚度有限，极易出现弹性形变。另外三套凸轮机构运行时相互影响，使整个机构产生振动，影响输出。因此建立机构的刚柔耦合虚拟样机进行分析。

本文利用有限元分析软件ANSYS将凸轮安装轴柔性化，替换原机构中的刚性轴，完成刚柔耦合虚拟样机的建立，如图12所示。

图11 安装轴柔性化

图12 刚柔耦合虚拟样机

3.2 刚柔耦合虚拟样机动态性能分析

对刚柔耦合虚拟样机进行仿真分析，设定凸轮轴转速为600r/min。得到以下曲线。

图13～图14与图8相比，角位移曲线基本一致，角速度和角加速度的变化趋势分别对应一致，且峰值相近；但图13大约在0.016s和0.086s附近的速度波动比图10刚性下的明显变大，并且图14中对应时刻的加速度出现明显冲击；同时加速度整体波动频率也比之前明显加快。

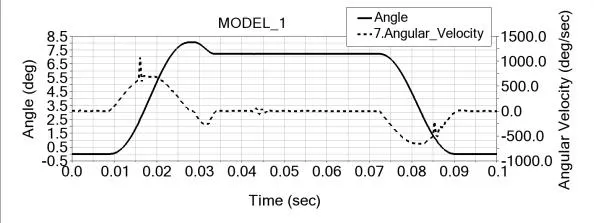
图13 压烟摆杆的角位移、速度曲线

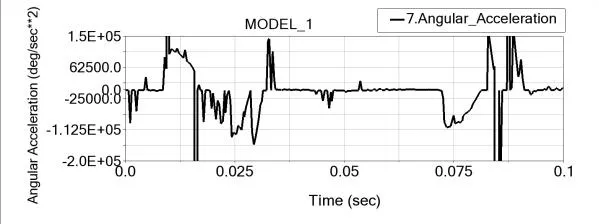
图14 压烟摆杆的角加速度曲线

图15、图16与图9相比，角位移曲线基本一致，其角速度和角加速度的变化趋势分别对应一致，且峰值相近；但图15中约在0.016s、0.043s和0.086s附近角速度波动变大，且图16中对应时刻的角加速度明显出现柔性冲击；同时图16中加速度波动频率整体加快。

图15 衬纸预折叠摆杆的角位移、速度曲线

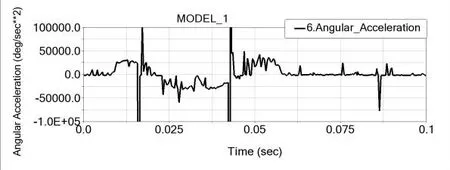
图16 衬纸预折叠摆杆的角加速度曲线

图17～图18与图10相比，角位移曲线基本一致，其角速度和加速度的变化趋势分别对应一致，且峰值相近；但图17中大约在0.016s、0.043s和0.086s附近的角速度波动比图10刚性下的明显变大，并且图18中对应时刻的角加速度明显出现冲击；同时图18中加速度整体波动频率比之前也明显加快。

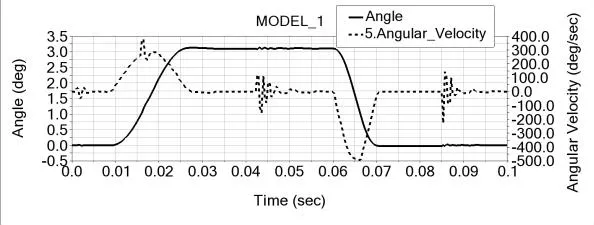
图17 护烟摆杆的角位移、速度图像

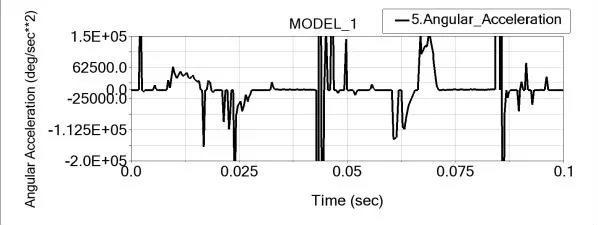
图18 护烟摆杆的角加速度曲线

综上所述，与刚性轴的仿真曲线相比，烟包裹包凸轮机构角位移曲线基本一致，其角速度和角加速度的变化趋势分别对应一致，且峰值相近，说明了结构的合理性。三个不同位置的凸轮机构在高转速下的惯性冲击会对凸轮轴产生不小载荷，使其产生微小变形，而凸轮安装轴的微小变形又导致凸轮和滚子的接触碰撞进一步被放大，因而将连接轴柔性化后其运动规律更加符合实际情况。

此外，速度和加速度产生冲击，并且各图的产生时间点相似，这说明三个凸轮机构互相影响，一个凸轮机构因接触碰撞而产生的振动会通过凸轮轴而影响其他凸轮机构，尤其是对护烟凸轮机构的影响最为明显，其在停歇段的0.043s和0.086s附近的速度和加速度冲击都太大，其分别由预折叠凸轮机构和压烟凸轮机构的动程段的冲击所影响产生。为此可以通过优化凸轮从动件结构以减小其质量，减轻惯性冲击；也可以适当改变护烟凸轮在轴上的安装位置或选择更高刚度的凸轮安装轴材料。

4 结语

本文基于ADAMS对烟包裹包凸轮机构进行了运动学和动力学分析，首先以压烟凸轮机构为例介绍了运动学模型求解的方法步骤；然后对整个烟包裹包凸轮机构机构在全刚性条件下仿真分析，得到其仿真曲线。最后，为了模拟实际工况，将凸轮轴柔性化后建立了裹包凸轮机构的刚柔耦合虚拟样机进行仿真，将仿真曲线与全刚性分析曲线对比后，发现输出的角位移与速度基本一致，但角加速度冲击更大、抖动频率更快，同时发现三组凸轮机构相互影响，且对护烟凸轮机构的影响最为明显，为此提出了改进措施，为进一步优化设计提供了依据。