基于鸣声组合特征与CNN 的电网危害鸟种识别
邱志斌,王海祥,廖才波,卢祖文,况燕军,张宇
(1.南昌大学信息工程学院,江西南昌 330031;2.国网江西省电力有限公司电力科学研究院,江西南昌 330096)
随着生态环境的不断改善,鸟类活动与电网运行的矛盾日益突出,涉鸟故障已成为导致输电线路跳闸的重要原因[1-3].引起电网故障的危害鸟种具有地区差异,且鸟种体型、习性、活动范围各异,所造成的故障类型与故障机理也各不相同[4].为了提高鸟害防治的有效性,电网运维人员需要了解并识别输电线路周边活动的鸟种,针对不同鸟种可能引起的故障类型采取差异化的防治措施.
鸟种识别的方法包括图像识别和鸣声识别,近年来,研究人员针对影响电网安全的鸟种开展了图像或鸣声识别研究.通过提取巡检图像中的鸟类形状、颜色和纹理等特征信息作为输入量,利用智能学习算法构建分类器[5],或者通过大样本数据集训练深度学习目标检测算法[6-7],可以实现鸟种图像识别.由于夜间活动或飞行中的鸟类图像采集存在一定困难,有必要将图像与鸣声信息共同作为电网危害鸟种识别的手段.鸣声识别是以鸟鸣信号作为特征提取对象,利用不同鸟类鸣叫声的差异性进行分类.
通过鸣声信息进行鸟种识别一般包括信号预处理、特征提取、算法识别等过程.常用的鸟类鸣声特征参数包含Mel 倒谱系数(Mel-frequency Cepstrum Coefficients,MFCC)[8-10]、Gammatone 倒谱系数(Gammatone Frequency Cepstrum Coefficients,GFCC)[11]、线性预测倒谱系数[12-13]、功率谱密度[14]、Mel 子带参数[15]和时频谱图特征[16-17]等.鸟种分类算法包括高斯混合模型[18-19]、隐马尔科夫模型[20-22]、随机森林[14,16,23]、支持向量机[15,24-25],以及卷积神经网络(Convolutional Neural Network,CNN)等深度学习算法[17-18,26-27].文献[15]通过Mel 滤波器组输出各个子带的能量序列,然后基于自回归模型分别对各个子带输出的随时间变化的能量序列进行建模,得到野外环境下11 种鸟类的鸣声参数化特征,并利用支持向量机进行分类.文献[17]利用动态系统扩充数据集,生成替代训练的数据,提取鸟鸣信号的时频谱图特征,结合CNN 对6 种鸟类进行分类.文献[19]以MFCC 作为特征参数,结合高斯混合模型对陕西省8种鸟类的鸣叫声和鸣唱声分别进行建模识别.文献[27]利用较容易获取的鸟类鸣声数据集和环境声音对ResNet-50网络进行训练,把训练好的模型迁移到鸣声获取较为困难的小数据集上进行分类,获得了79%的准确率.文献[28]对MFCC 和GFCC 进行融合,利用CNN对环境声音进行分类,结果表明融合特征分类模型具有更高的识别精度.目前,对鸟类鸣声的识别研究多是在较小的数据集上进行种类较少的鸟种分类,且使用单一的鸟鸣特征.由于输电线路跨越距离较长,沿线经过不同的地理环境,涉及的危害鸟种具有多样化特点.为了辅助涉鸟故障防治,提高危害鸟种的识别准确率,有必要在多种类大数据集上开展鸟种鸣声识别研究.
本文针对与输电线路相关的23 种鸟类,通过对收集的鸣声信号进行降噪与剪辑等预处理,构建了包含3 290段鸣声信号的数据集,然后计算鸟鸣信号的MFCC、GFCC 和短时能量(Short-term Energy,STE)特征,经过组合与归一化后得到新的特征集,将其作为CNN模型的输入,对网络进行训练,利用Softmax 层进行分类识别.算例结果表明,本文所提出的方法对涉鸟故障相关鸟种具有较高的识别率,可为运维人员开展输电线路鸟种识别与涉鸟故障防治提供参考.
1 鸟种鸣声信号处理
1.1 鸣声信号降噪与剪裁
由于鸟种鸣声信号大多是在野外条件下采集的,其中含有大量噪声,为了获取更加清晰的鸣声信号特征,提高鸟种鸣声识别的准确率,需要对鸟鸣信号进行降噪处理.鸟鸣信号中含有的噪声多为风声和流水声,可以看作加性噪声.本文采用改进谱减法去除鸟鸣信号中的这类背景噪声.
谱减法[29-30]是一种有效的降噪方法,在噪声处理与语音增强方面应用广泛.其基本原理是采用带噪鸟鸣信号的功率谱减去噪声段的平均能量值,从而得到降噪后的鸟鸣信号.已知鸟鸣信号前导噪声段对应的帧数为T,采用Xi(k)表示经过快速傅里叶变换后的鸟鸣信号,则噪声段的平均能量值D(k)可表示为:

式中:i为第i帧;k为第k条谱线;|Xi(k)|为第i帧每个频率分量的幅值.谱减法的计算方法为:
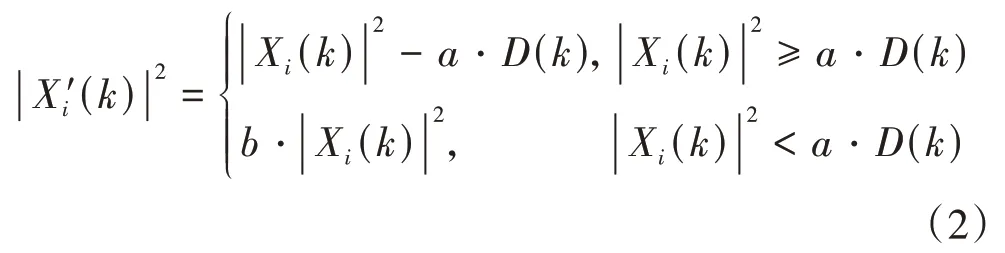
式中:a为过减因子;b为增益补偿因子;|X′i(k)|表示谱减后的第i帧每个分量的幅值.
式(2)利用每一帧的值进行谱减,降噪效果较差,为得到较小的谱估算方差,提高鸟鸣音频中环境噪声的降噪效果,改进谱减法采用鸟鸣信号相邻帧之间的平均值Yi(k)代替式(2)中的Xi(k)进行谱减计算.Yi(k)的表达式为:
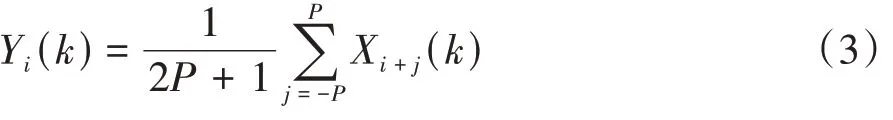
对于第i帧,在Xi-P(i),…,Xi(k),…,Xi+P(k)之间计算其平均值Yi(k).
此外,由于鸟鸣信号中噪声是随机的,在降噪过程中会存在噪声谱线的谱值大于a·D(k)的情况,若按式(2)进行计算会导致噪声不能被完全消除.改进谱减法在降噪过程中从前导噪声段保留了噪声的最大值,利用噪声最大值对含噪声频进行谱减,从而在谱减过程中尽可能减少噪声残留.本文将功率谱作为谱减对象,取式(3)中的P=1,即在相邻3帧之间取平均值Yi(k)进行谱减计算.以高危鸟种大杜鹃的一段鸣声信号为例,原始大杜鹃鸣声信号如图1(a)所示,经过改进谱减法降噪后的鸣声信号波形如图1(b)所示.可见,改进谱减法有效滤除了原始鸣声信号中的噪声,使得鸟鸣信号更加清晰.
降噪后的鸟种鸣声信号大多持续时间较长,而且可能包含其他鸟类鸣声的干扰,为了节约计算资源并减少干扰,需要对降噪后的鸟鸣信号进行剪裁.自然界中,绝大多数鸟类一声鸣叫的时间都在1 s 以内.因此,本文将鸟鸣信号样本均剪裁为1 s,构建鸟鸣样本集,用于特征提取.以图1(b)中的大杜鹃信号为例,剪裁为1 s后的信号波形如图1(c)所示.

图1 大杜鹃鸣声信号预处理效果Fig.1 Preprocessing results of a cuculus canorus sound signal
1.2 涉鸟故障相关鸟种鸣声样本集
根据电网运行部门关于历史涉鸟故障及相关鸟种的统计结果,本文以某省电网引起输电线路涉鸟故障的13种高危鸟类、8种微害鸟类和2种无害鸟类为对象,构建23 种鸟类的鸣声信号样本集,每种鸟类的样本数目为106~209 个不等,共计3 290 个样本,其中高危、微害和无害鸟种样本数量分别为1 848、1 193和249,每个样本时长均为1 s,采样频率为16 kHz.上述用以鸣声识别研究的电网涉鸟故障相关鸟种样本数量及导致的故障类型如图2 所示.为保证数据集的可信度和真实性,采用不同噪声环境和录音条件下的鸟类鸣声构建数据集,同一段鸣声不重复使用.
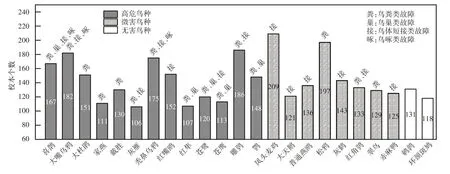
图2 电网涉鸟故障相关鸟种鸣声样本分布Fig.2 Sound sample distribution of bird species related to power grid faults
2 鸟种鸣声特征提取
2.1 短时能量
短时能量是鸟鸣信号时域特征,由于不同的鸟鸣音节之间能量差别十分显著,因此可以通过短时能量的变化来分析不同鸟种的发音特点.已知降噪后并进行分帧加窗处理的鸟鸣时域信号为xi(u),短时能量Est(i)的计算公式为:
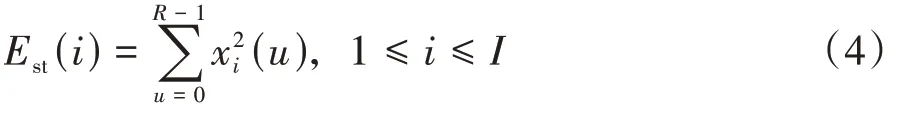
式中:R表示帧长;I表示鸟鸣音频总帧数.
2.2 MFCC特征参数
MFCC特征是声音识别领域最常用的特征之一,它将时域信号转化为频域,然后基于人耳的听觉机理来分析语音频谱,具有特征表达准确、特征维度低的优点.MFCC提取流程如下:
1)计算每一帧信号的线谱能量Ei(k),即

2)将每一帧信号的线谱能量通过Mel 滤波器组,计算在Mel滤波器组中的能量Si(m),即
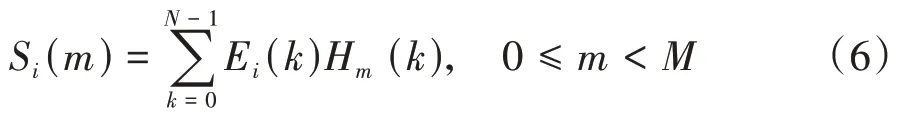
式中:m表示滤波器编号;M为滤波器的个数;Hm(k)为滤波器的频率响应;N为谱线条数.
3)将通过Mel 滤波器的能量取对数后进行离散余弦变换(Discrete Cosine Transform,DCT),得到鸟鸣信号的MFCC特征参数,即

式中:d为进行DCT 后的谱线,1≤d≤D,D为MFCC 特征维数.通过式(7)计算得到的MFCC 特征参数为二维矩阵,将其转化为图像,横、纵坐标分别表示帧数和特征维度,采用颜色深浅代表参数值大小,即可得到鸟鸣信号的MFCC特征图.
2.3 GFCC特征参数
鸟鸣信号的GFCC 特征与MFCC 特征提取流程的主要差别在于使用的滤波器不同,GFCC 特征是将鸟鸣信号输入n通道的Gammatone 滤波器[31],其表达式为:
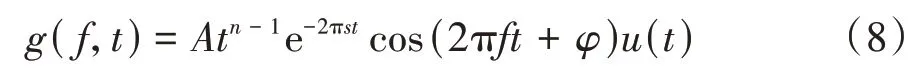
式中:f、t、φ分别为频率、时间和相位;A为滤波器增益的常数;n为滤波器的阶数;u(t)为单位阶跃函数;s为滤波器带宽,其计算式为:
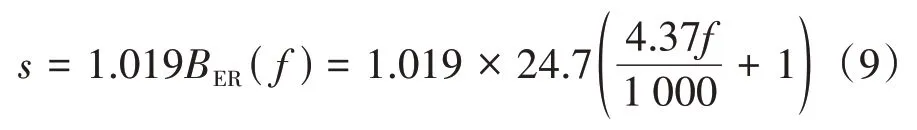
式中:BER(f)为等效矩形带宽.
Gammatone 滤波器对鸟种鸣声信号的滤波过程可以表示为:
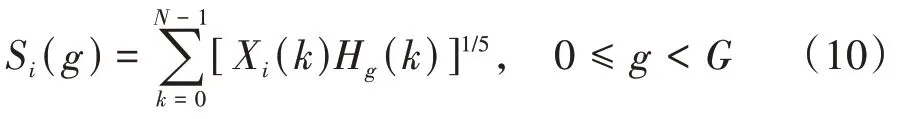
式中:Si(g)为第g个滤波器输出的对数能量值;Hg(k)为Gammatone 滤波器频率响应;g为滤波器编号;G为滤波器的个数.对每个滤波器的输出取对数后进行离散余弦变换,其表达式为:
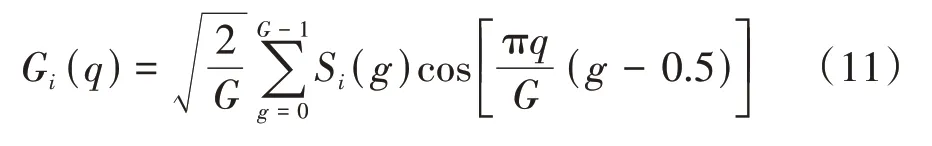
式中:Gi(q)为第q维GFCC 特征参数,1≤q≤Q,Q为GFCC特征维数.
2.4 组合特征
鸟鸣识别相较于人类声音识别更为困难,单一类型特征往往无法对鸟鸣特点进行完全表达,故需要进行特征的组合.由于GFCC特征与MFCC特征使用不同的滤波器组,二者组合能够有效改善MFCC特征能量泄漏问题,而GFCC 和MFCC 特征都是频域特征,引入短时能量可以增加时域信息.所以本文将MFCC 特征及其一阶差分、GFCC 特征及其一阶差分和短时能量特征进行组合,然后删除差分为零的帧,经过归一化得到鸟种鸣声的组合特征集.组合特征计算流程如图3所示,相关计算参数如表1所示.
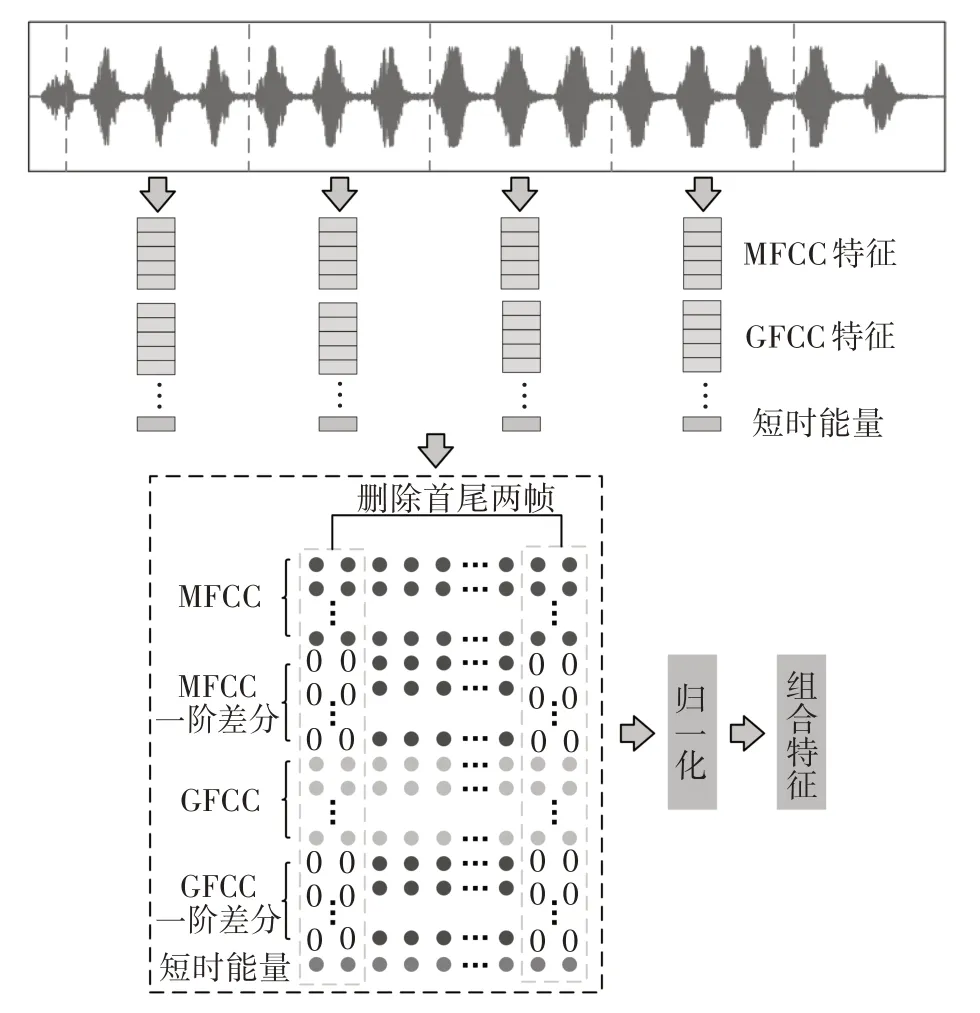
图3 组合特征计算流程图Fig.3 Flow chart of combined feature calculation

表1 组合特征相关计算参数Tab.1 Parameters related to the combined features
MFCC 和GFCC 特征都属于静态特征,为了获取鸟鸣信号的动态特性,对MFCC 和GFCC 特征的一阶差分进行计算.同时,为了降低信号中的毛刺对一阶差分动态特征的影响,计算相邻三帧的一阶差分并求取其平均值.以MFCC 特征为例,一阶差分特征的计算方法为:
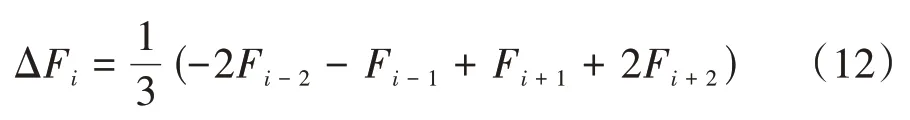
以图2所示的大杜鹃鸣声信号为例,取MFCC 和GFCC 特征维数均为12,通过上述方法计算所得的MFCC 特征图、GFCC 特征图、二者的一阶差分特征图以及组合特征图如图4所示.

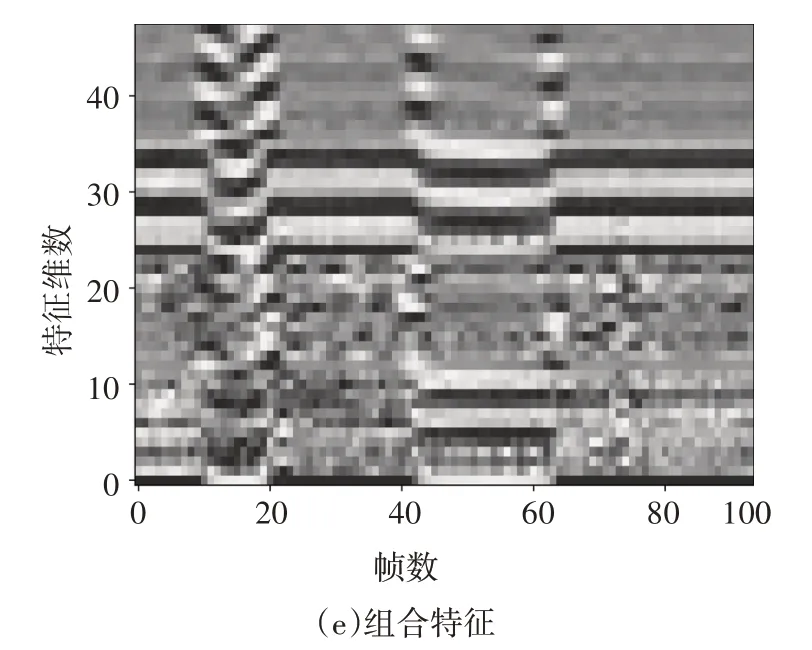
图4 大杜鹃鸣声信号的特征参数图Fig.4 Sound signal feature diagrams of cuculus canorus
将上述不同特征进行组合,可以对鸟种鸣声包含的听觉信息进行综合表征.组合特征集的维数由MFCC、GFCC 和短时能量特征维数决定.由于一阶差分是通过对不同帧进行差分运算,差分前后特征维数不变,而短时能量特征只有一维,故组合特征维数为2(D+Q)+1,不同特征的维度如表2 所示.由于采用相邻三帧计算差分的方法,导致首尾两帧一阶差分值为不包含信息的零值,因此将首尾两帧删除.
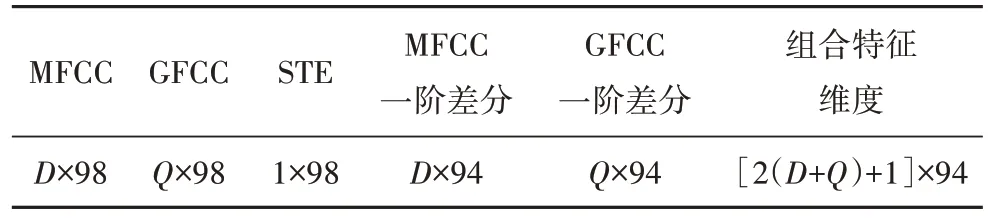
表2 组合特征的维度Tab.2 Dimensions of the combined features
鸟种鸣声的短时能量、MFCC 特征与GFCC 特征的计算方法不同,导致数值上存在较大差异,为防止特征尺度与量纲不同对识别结果造成影响,需要将各个特征量归一化到[0,1].特征量归一化方法为:

式中:Fmax和Fmin分别表示特征量F的最大值和最小值.以大杜鹃的鸣声信号为例,将各个特征量进行归一化后,组合特征如图4(e)所示.
3 电网危害鸟种鸣声识别算例
3.1 卷积神经网络
本文构建24 层卷积神经网络用于鸟种鸣声特征的训练与鸟种识别,网络主要包含5 个卷积层+ReLU、5 个批量归一化层和4 个池化层.卷积核和池化核大小分别为[3×3]和[2×2],设置卷积步幅为1,池化步幅为2.卷积神经网络结构如图5所示.
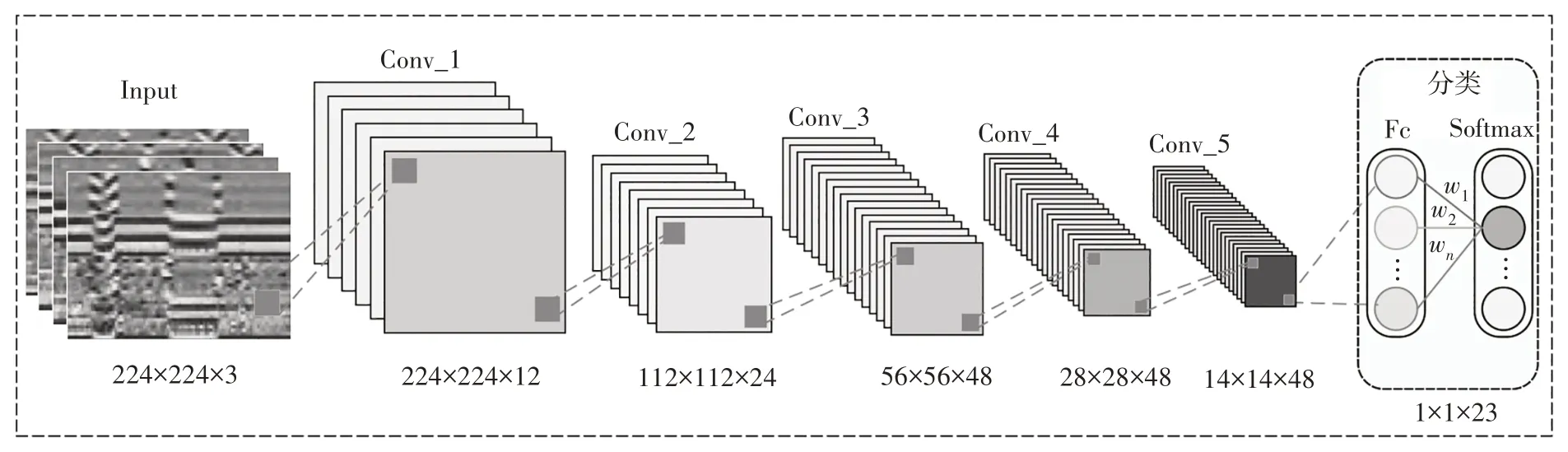
图5 卷积神经网络结构Fig.5 Structure of the convolutional neural network
网络输入大小为224×224×3,将保存为相同大小的组合特征作为网络的输入,经Conv_1、Conv_2、Conv_3 卷积层进行卷积,通道数分别为12、24 和48,卷积前后特征大小保持不变.在每次卷积之后进行池化操作,池化以后通道数目不变,特征大小变为原来的1∕2.Conv_4 和Conv_5 的卷积核个数都为48,卷积前后特征图大小和通道数均保持不变,卷积后的池化层使特征大小变为原来的1∕2,最终输出大小为14×14×48,经过全连接层后输出一个包含23 种鸟类可能性的概率分布.
3.2 仿真环境与参数设置
本文开展的电网危害鸟种鸣声识别算例是在Matlab 2021a 的软件环境以及CPU 为AMD Core R7-5800H、主频3.2 GHz、16 GB 内存,GPU 为NVIDIA GeForce RTX3060、显存大小为6 GB 的硬件环境下完成.采用小批量梯度下降法(Mini-Batch Gradient Descent,MBGD)进行网络优化,设置批大小为16,最大轮数为8,初始学习率为0.000 3,每经6 轮训练学习率降低为原来的50%,由此对23 种鸟类鸣声信号进行分类识别.
3.3 算例及结果分析
利用本文构建的涉鸟故障相关鸟种鸣声样本集对CNN 进行训练,识别鸟种鸣声,具体流程如图6所示.
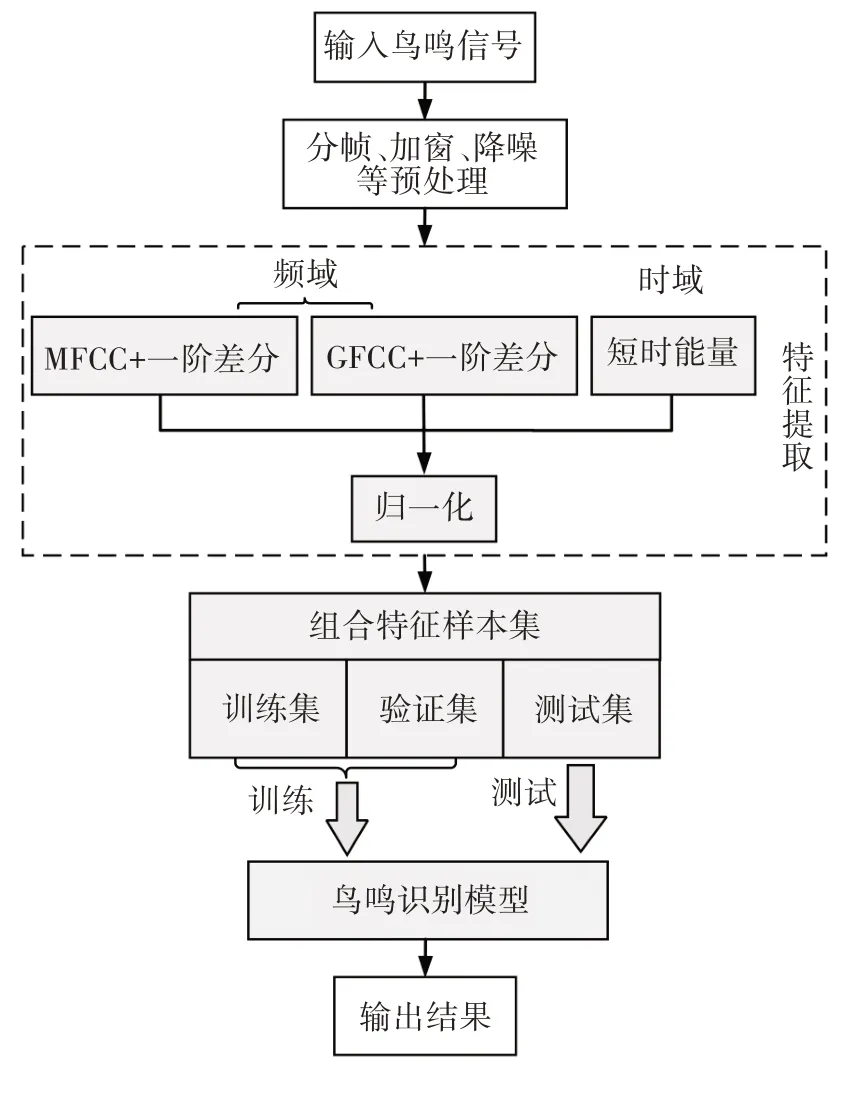
图6 鸟种鸣声识别流程图Fig.6 Flowchart for sound identification of bird species
由于不同的数据集划分比例会对识别结果产生影响,分别按照训练集、验证集和测试集比例为8∶1∶1、7∶1∶2、7∶2∶1 和6∶2∶2 划分数据集,设置组合特征维度为57 维时对网络进行训练,识别结果如表3 所示.可见,当数据集划分比例为8∶1∶1 时验证准确率最高为91.49%,测试准确率最高为91.21%.
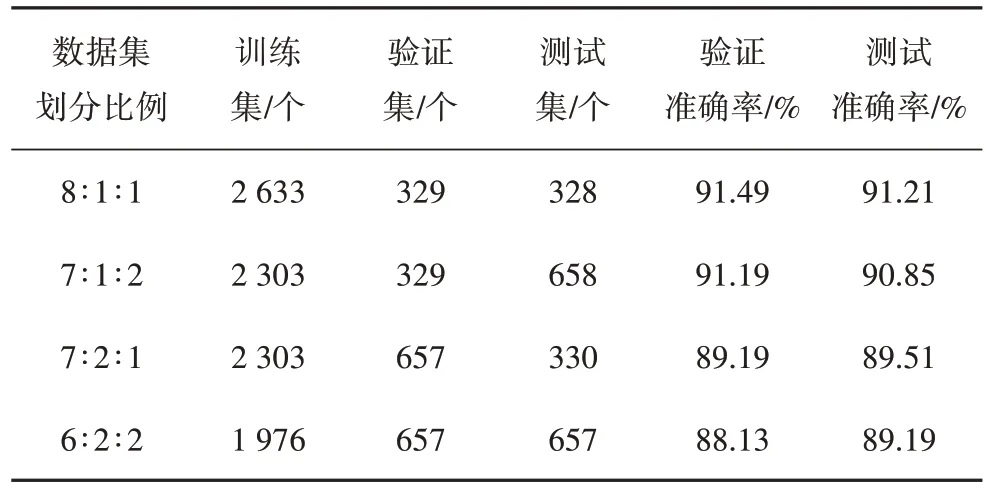
表3 不同数据集划分比例下的识别结果Tab.3 Identification results under different division proportions of data set
为了探究组合特征集的识别效果,设置数据集划分比例为8∶1∶1,同时以MFCC、GFCC、MFCC+STE、GFCC+STE、MFCC+GFCC 作为CNN 模型的输入,将其作为对照组.当MFCC 和GFCC 的特征维数D、Q均取12 时,以验证集准确率作为评价指标.上述各组特征集对应的CNN训练结果如图7所示.

图7 不同鸣声特征下的CNN训练结果Fig.7 CNN training results with different bird sound feature set
由图7 可知,采用单一MFCC 和GFCC 特征作为输入对CNN 进行8 轮训练后,验证准确率分别为88.75%和88.14%;引入短时能量STE 特征后,验证准确率提升为89.06%和89.67%.采用MFCC+GFCC组合特征作为网络输入后,验证准确率可进一步提升至91.50%.以本文组合特征作为输入时,CNN 模型的验证准确率达到了92.40%,相比于5 个对照组分别提高了3.65%、4.26%、3.34%、2.73%和0.9%,这一结果表明,采用组合特征作为网络输入,可使CNN取得更好的训练效果.
MFCC 和GFCC 特征包含的鸟种鸣声信息量受到特征维数D和Q的影响,特征维数低,包含的鸟鸣信息较少;特征维数高,则干扰更为严重且计算量增大,占用更多计算资源.为了研究组合特征维数对识别结果的影响,设置数据集划分比例为8∶1∶1,D=Q且分别取值6、10、14、18、22、26,即组合特征维数分别为25、41、57、73、89 和105,比较不同特征维数下CNN 模型的验证集准确率,结果如图8所示.可见,当组合特征维数从25增加至73时,验证准确率逐渐增大,分别增大至86.63%、90.58%、91.50%、93.31%;当特征维数增加至89和105时,验证准确率反而下降,分别下降至91.79%和90.58%.因此,本文取73 维组合特征训练后的CNN模型用以测试集的鸟种识别.
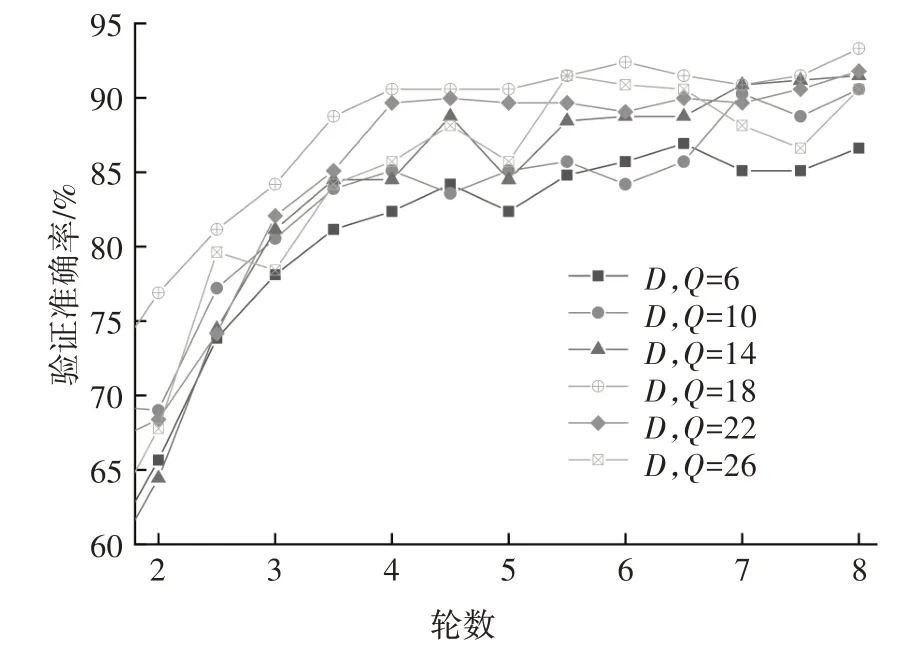
图8 不同特征维数下的CNN训练结果Fig.8 CNN training results with different feature dimensions
采用训练后的CNN 模型对23 种鸟类鸣声测试集进行识别,结果如图9所示.由图9可知,识别正确率分布在61.1%~100%内,总体识别正确率可达92.2%.13 种高危鸟类和8 种微害鸟类的平均识别正确率分别为94.3%和89.9%,高危鸟种鸣声的识别效果表现更为优异,其中大杜鹃、戴胜、苍鹭等8 种高危鸟种,大天鹅、松鸦、翠鸟3 种微害鸟种的测试样本识别正确率均为100%,其余5种高危鸟种和5种微害鸟种的识别正确率为61%~80%的有2种,为81%~90%的有5 种,在90%以上(不包含100%)的有3 种.无害鸟种作为干扰选项仍然具有较好的识别效果,鹌鹑和环颈斑鸠的识别正确率分别为92.3%和83.3%.
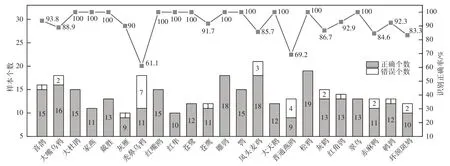
图9 鸟种鸣声测试集的识别结果Fig.9 Recognition results of bird sound signals in test set
在样本预测类别结果中,大嘴乌鸦对其他鸟种识别的干扰最为严重,5 个秃鼻乌鸦、2 个赤麻鸭样本均被错误识别为大嘴乌鸦.秃鼻乌鸦识别正确率最低,这是由于同科鸟种鸣声非常相似,造成了识别难度增大.以苍鹰、鹗、凤头麦鸡、喜鹊、大杜鹃、大天鹅6 种鸟类的其中一个鸣声样本为例,其识别结果如图10所示.由图10可知,确定概率均在83%以上,说明网络模型对测试集具有较好的识别效果.
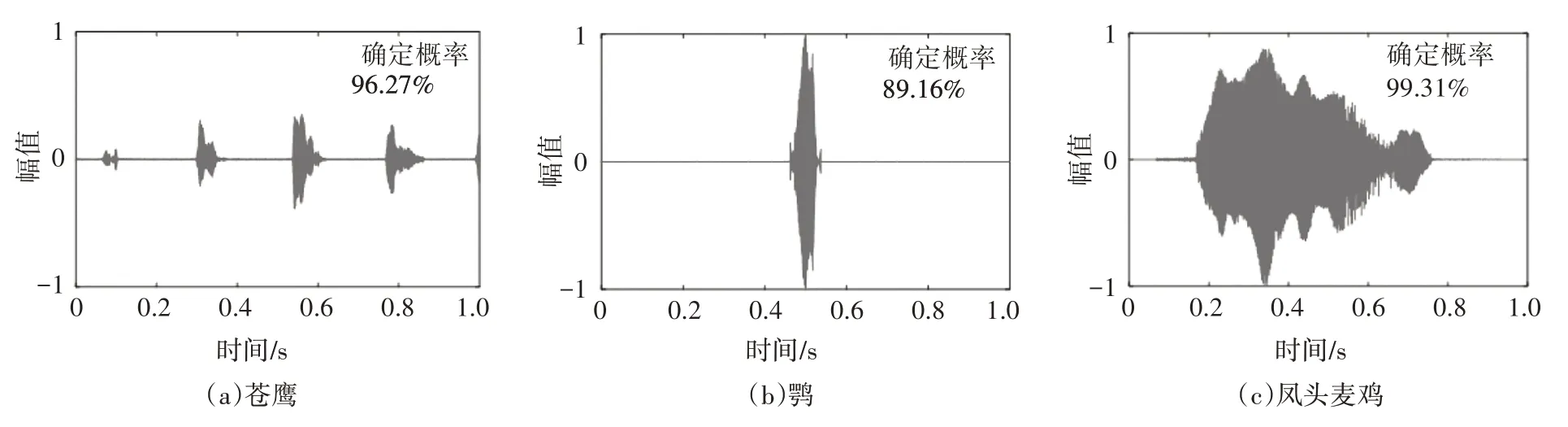
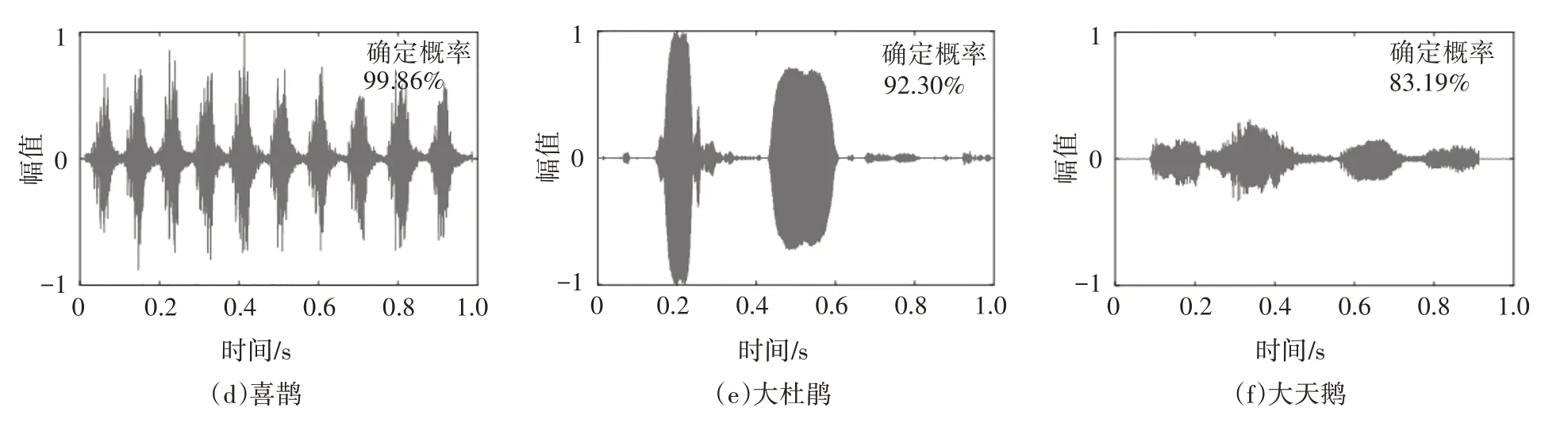
图10 部分鸟种的识别结果和确定概率Fig.10 Recognition results and determinate probabilities of some bird species
4 结论
本文提出了一种用以电网涉鸟故障危害鸟种识别的方法.通过对鸟种鸣声信号进行降噪等预处理,提取MFCC、GFCC 与短时能量等构成鸣声组合特征集.采用CNN 构建鸟种识别模型,按照8∶1∶1比例划分训练集、验证集和测试集,以73 维组合特征作为模型输入时可取得最优识别效果.对23 种输电线路涉鸟故障相关鸟种的整体识别正确率可达92.2%,其中高危鸟种可达94.3%.本文研究可为电网运维人员开展鸟种智能识别与差异化防治提供参考.

