交流侧不对称故障下柔性直流输电系统优化控制研究

夏向阳，易海淦，夏天，，石超，贺烨丹，刘代飞，邓文华，王灿

（1.长沙理工大学电气与信息工程学院，湖南 长沙 410114；2.长沙理工大学能源与动力工程学院，湖南 长沙 410114；3.湖南长高高压开关有限公司，湖南长沙 410001）

我国资源与负荷地域分配严重不均的特点，决定了必须采用远距离、大容量跨区域高压输电的方式来输送电能［1-3］.其中柔性直流输电系统是当下跨区域大容量高压直流输电的首选方式［4-5］.

在柔性直流输电系统中，交流电网电压不对称会使得MMC 换流器交流侧电流不平衡［6-8］，环流中出现零序分量，直流侧产生功率振荡等问题.电网电压对称时MMC 的控制策略采用的是和两电平VSC一样的矢量控制策略，但该策略无法控制负序电流［9-10］.尤其是在不平衡网压下，交流电压没有实现正负序分离，电压中的基频负序分量中含有二倍频的交流量，导致锁相环的提取精度降低.

文献［11］将有限状态分层模型预测控制引入到MMC 控制中，解决了权重因子设计问题，但环流问题没有得到解决.文献［12］提出了一种电网电压不平衡下MMC 的无源控制策略，该策略能够很好地实现交流侧的控制目标.文献［13］提出了一种无差拍直接功率控制策略，但有功的二倍频波动没有得到完全抑制.文献［14］设计了基于比例谐振调节器和瞬时功率理论的控制策略，但会明显降低其响应速度.文献［15］分别对交流侧电流、桥臂环流和直流电流进行解耦控制，针对系统暂态性能进行了提升.文献［16］提出了一种综合控制策略，能实现交流侧电流对称，并且引入零序电流抑制器，消除零序分量对直流侧的影响.上述策略都没有考虑不平衡网压下环流抑制精度和相应速度之间的平衡，这也是目前不平衡网压下研究待解决的问题.

针对以上不足，为提高MMC 在复杂工况下的故障穿越能力，本文提出一种在网压不对称工况下MMC-HVDC 的优化控制策略.设计基于双二阶广义积分器锁相环在不对称工况下获取电压的相位和频率信息，保证电压电流正负序dq轴分量的准确提取，提升了交流侧电流控制的精度，配合双矢量控制器实现三相电流平衡；利用由PI 控制器和重复控制器串联组成的嵌入式重复控制器，在无静差跟踪环流直流分量参考指令的同时，能有效抑制环流中的二倍频正负零序分量，优化系统性能，提升故障穿越能力，并在仿真软件MATLAB∕Simulink 中搭建MMCHVDC系统仿真模型，验证了所提优化控制策略的有效性.

1 MMC 拓扑结构和工作原理

为了简化数学建模的过程，忽略电力电子器件的驱动延时和死区时间，认为所有子模块结构一致，根据仿真速度最快的平均值模型进行数学建模.MMC桥臂简化平均值模型如图1所示［17］.

图1 MMC桥臂简化平均值模型Fig.1 Simplified average model of MMC bridge arm

图1 中，桥臂所有子模块的等效电容值为C∕N；L0+R0为桥臂电感和损耗等效电阻串联；电感Lac和电阻Rac为交流电网阻抗；icpj、icnj分别为上桥臂和下桥臂中流过子模块电容的电流；upj、unj分别为上桥臂和下桥臂级联子模块经调制后输出的电压；ucpj、ucnj分别为上桥臂和下桥臂N个级联子模块电容电压等效为理想变换器产生的可控电源；ipj、inj分别为上桥臂和下桥臂流过的电流；Udc为直流母线电压；Idc为直流侧电流；usj、isj分别为交流侧各相电压和电流；j=a、b、c.

根据基尔霍夫定律，可得MMC 基本单元的时域动态数学方程为：

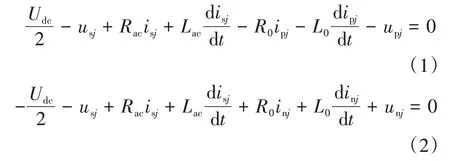
将式（1）与式（2）相加，进行化简整理可得：

式中：R=Rac+0.5R0；L=Lac+0.5L0；ej=0.5（unj-upj）.

将式（1）与式（2）相减，可得：

定义桥臂环流idiffj和桥臂共模电压ucomj的表达式分别为：

联立式（3）～式（6），可得环流在桥臂阻抗上的不平衡压降udiffj为：

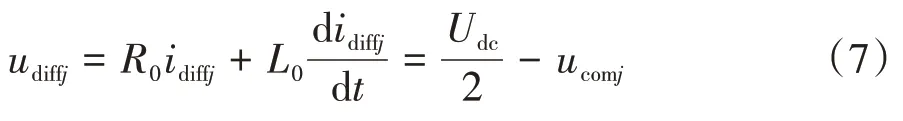
式（7）的右边部分就是MMC 直流回路的数学模型，描述了MMC内部的电压电流特性.

上桥臂和下桥臂的电压也可以分别用两种形式表示：

2 不对称工况下MMC运行特性分析

2.1 MMC交流侧功率波动分析

电网电压不对称会使得三相电流不平衡，有功功率和无功功率产生不可控振荡，而在电网发生不对称故障时，情况会更加严重.

本文以交流电网发生单相接地故障为例，对MMC 交流侧的功率特性进行分析.MMC-HVDC 系统单线结构如图2 所示.图2 中，MMC 换流站经联结变压器接入交流电网，联结变压器采用Yg∕△接线方式，在PCC 点发生单相接地故障时，MMC 的阀侧电压电流中不存在零序分量.

图2 MMC-HVDC系统单线结构Fig.2 Single line structure of MMC-HVDC system

根据对称分量法，阀侧的j相交流电压和电流可以正负序分解为：

对式（9）进行旋转坐标变换，得到dq坐标系下阀侧电压和电流的表达式分别为：

根据瞬时功率理论，可得两相旋转坐标系下MMC交流侧的瞬时复功率为［12］：

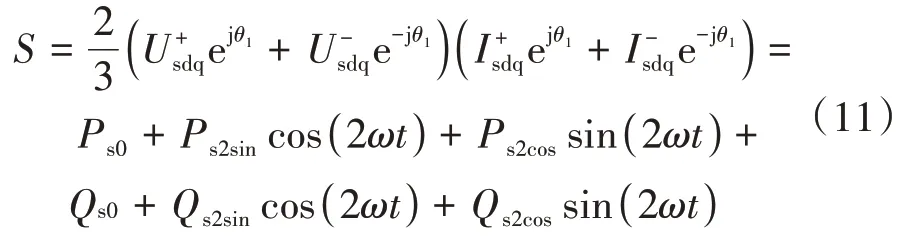
式中：S为复功率；θ1为d轴和两相静止坐标系下α轴之间的夹角，且a轴与α轴位置重合；Ps0、Qs0分别为交流侧有功功率和无功功率的直流分量幅值；Ps2sin、Ps2cos、Qs2sin、Qs2cos分别为有功功率和无功功率中对应的二倍频分量幅值.

在不对称电网电压下，交流侧电流的控制目标可分为抑制负序电流、抑制有功功率脉动、抑制无功功率脉动.不同的控制目标根据式（12）可计算得到不同的内环输出电流控制参考值.

式中：k=0、1、-1.当k=0 时，交流侧电流控制目标为抑制负序电流，实现三相电流平衡；当k=-1 时，交流侧电流控制目标为抑制有功功率脉动；当k=1 时，交流侧电流控制目标为抑制无功功率脉动.

由于电压及电流负序分量的出现，会使得桥臂子模块电容电压存在较大波动，甚至引起短路电流过大导致功率器件电流超限，此时若不进行故障穿越控制，会严重影响换流器的正常运行甚至系统停运.为确保系统过电流不会危及电力电子器件安全，本文将交流侧电流的控制目标选择为抑制负序电流.

2.2 MMC桥臂环流分析

在正常工况下，MMC 桥臂环流中的二倍频交流分量呈现的是负序性质.而当交流侧发生不对称故障时，交流侧三相电流的不平衡，使得三相桥臂分配的有功功率不一致，从而使环流的成分更加复杂.因此，需要对环流的成分进行具体的分析以便设计合适的环流抑制策略.

在网压不平衡情况下，MMC 的内部电动势ej可以正负序分解为：

式中：E+、E-分别为内部电动势正负序分量的幅值；θ+、θ-分别为内部电动势正负序分量的相位.

由文献［18］可知，在网压不对称工况下，三相桥臂环流中的直流分量不一定相等.本文以a 相桥臂为例，简单介绍环流参考值的计算过程.

忽略桥臂阻抗损耗，根据瞬时功率理论可得a相上桥臂和下桥臂功率之和Pa为：

Pa中的直流功率分量Pa0可以表示为：

假设各相桥臂能量已经平衡，如果此时桥臂功率中直流分量Pa0幅值不为0，那么子模块平均电容电压将处于变化的状态，不利于系统的稳定运行.因此，需要令桥臂功率中的直流分量Pa0为零，从而解出桥臂各相环流直流分量的表达式如下所示［19］：

在网压不对称工况下，环流控制的目的依然是抑制环流中除直流分量外的偶次谐波分量.因此，计算得到的环流直流分量值就可以当作是桥臂环流的参考值.

桥臂环流的参考值中包含了交流侧电压、电流的正序和负序分量，当电压电流的负序分量都为0时，各相环流的直流分量参考值都相等；但当交流侧选择的控制目标为抑制电流中的负序分量时，负序电压的存在会使得三相桥臂环流中的直流分量不相等.同时，由于环流的参考值中不包含交流分量，因而只要环流控制器能够无静差跟踪环流直流参考指令，便能实现对环流中二倍频正负序零分量的有效抑制.

3 不对称工况下MMC-HVDC 系统控制策略

在不对称工况下，MMC-HVDC 控制系统首先需要抑制交流侧的负序电流，以降低其对MMC 运行的影响.此外，由于MMC 内部的二倍频零序环流分量会流入到直流侧中引起有功功率的振荡，也需要将其抑制.因而后文控制策略的设计主要围绕这两者展开.

3.1 基于双二阶广义积分器的锁相环设计

交流侧电流控制策略采用文献［7］所述的dq轴坐标系下的内环双序交流侧电流控制器.考虑到该控制器的结构比较成熟，限于篇幅，本文主要介绍利用DSOGI-PLL 提取电压电流正负序dq轴分量的过程.

在电网电压对称的情况下，MMC 控制系统采用的是基于同步坐标系的锁相环（Single Synchronous Reference Frame Software-Phase Locked Loop，SSRFPLL）.当电网电压不对称时，交流电压没有实现正负序分离，电压中的基频负序分量经派克变换后变为二倍频的交流量，SSRF-PLL中的PI控制器无法对交流量实现无静差跟踪，导致锁相环的精度会受到较大的影响.

为了获取用于坐标变换的不对称电网电压下精确的电压相位信息和频率信息，本文设计了DSOGIPLL，可以通过二阶广义积分器（Second Order Generalized Integrator，SOGI）产生正交信号滤除谐波，并在电网电压不对称的情况下，实现对基波电正负序分量的精确提取.其中SOGI的结构如图3所示.

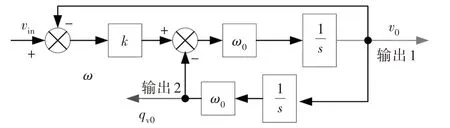
图3 二阶广义积分器Fig.3 Second order generalized integrator

图3中，vin为输入信号；v0和qv0分别为输出信号1和2；ω0为谐振频率；k为增益.

输出信号与输入信号间的传递函数可以表示为：

在SOGI 中，v0和qv0能够输出与vin同频率的交流信号，并且qv0的相位总滞后v090°.当SOGI 的谐振频率设置为电网基波频率时，输入信号中含有的谐波成分都能被有效滤除，实现输出信号对输入基波信号的无静差跟踪.根据SOGI 输入输出的传递函数，绘出不同增益k下的伯德图，如图4 所示.由图4 可知，两个输出信号都对除基频分量外的谐波有较高的衰减，并且参数k的取值越小，滤波效果越好.图5 为不同k值下输出信号1 的阶跃响应曲线，由图5 可知，k值越小，动态响应速度越慢.所以在SOGI 的设计过程中，一般采取折中的方法选取k值，本文取1.414.

图4 DSOGI的输入输出伯德图Fig.4 Input output Bode diagram of DSOGI

图5 D1（s）的阶跃响应曲线Fig.5 Step response curve of D1（s）

设计好DSOGI 后，再结合正负序分量计算模块（Positive and Negative Sequence Control，PNSC）以及SSRF-PLL 就得到了DSOGI-PLL，其结构如图6 所示［19］.DSOGI-PLL 首先采集交流侧电压信号进行克拉克变换，利用SOGI 输出信号的正交和滤除谐波特性，实现对输入电压基频信号的正交分相；再由正负序分量计算环节计算得到两相静止坐标系下的基频正负序电压分量，将基频正序电压分量输入到SSRF-PLL中，通过PI控制，完成锁相，最终实现对相位和频率的精确提取.利用DSOGI-PLL 输出的相位和频率信息，对分离后的两相静止坐标系下的电压基频正负序分量做派克变换，即可得到精确的正负序dq轴电压分量.

图6 DSOGI-PLL 整体结构Fig.6 Overall structure of DSOGI-PLL

3.2 基于嵌入式重复控制器的桥臂环流抑制

在环流控制方式的选择上，基于内模原理的重复控制器可以准确跟踪周期性信号及倍数次谐波，适用于抑制环流，但无法跟踪直流参考指令，并且重复控制器在暂态过程中会延迟一个周波输出，导致控制速度比较慢.而PI 控制器和重复控制器组成的复合控制方式则能有效解决上述问题，并且同时兼顾了PI控制器控制速度快和重复控制器谐波抑制能力强的优点［20］.

基于串联型结构的嵌入式重复控制器（PI-RC）桥臂环流抑制详细框图如图7所示.

图7 基于嵌入式重复控制器的桥臂环流抑制框图Fig.7 Arm circulating current suppression based on embedded repetitive controller

从误差信号ierr到参考指令信号的传递函数可以表示为：

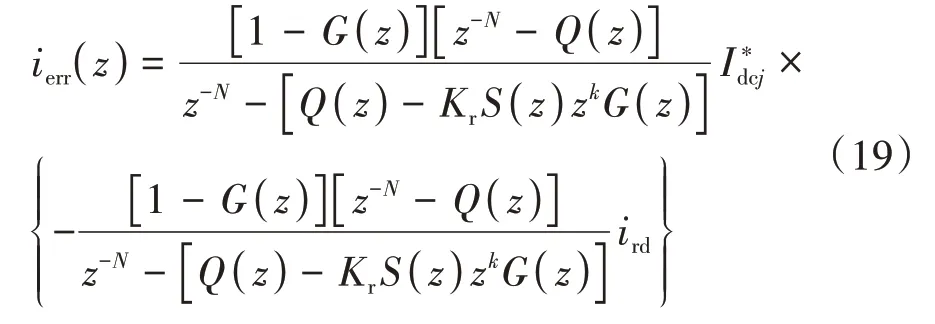
式中：G（z）为嵌入式重复控制器中重复控制器的控制对象.G（z）的传递函数可以表示为：

嵌入式重复控制器的设计过程主要由以下几个部分组成：

1）内膜1∕［1-Q（z）z-N］.Q（z）是内模中的重要环节，Q（z）对积分效果有一定减弱作用，为了提升控制器的鲁棒性能，Q（z）通常选小于1 的常数或者零相移低通滤波器，本文取0.95.内膜的幅频特性如图8所示，由图8可知，谐波具有良好的抑制效果.

图8 内膜的幅频特性Fig.8 Amplitude frequency characteristics of intima

2）补偿环节KrS（z）zk.S（z）的作用是使S（z）G（z）在中高频段的增益快速衰减，而在中低频段的增益为1，从而保证控制系统的稳定性.本文选用二阶低通滤波器，取自然频率ωn=10ω1，阻尼比ξ=1.S（z）的伯德图如图9 所示，由图9 可知，滤波器在高频段增益衰减迅速，提高了系统的稳定性.

图9 S（z）的伯德图Fig.9 Bode chart of S（z）

超前环节zk用于相位补偿，zk与S（z）G（z）的相频特性如图10 所示.由图10 可知，当k=-6 时，效果最好，在截止频率内两者几乎吻合，表明其能够有效抵消S（z）G（z）的相位滞后.

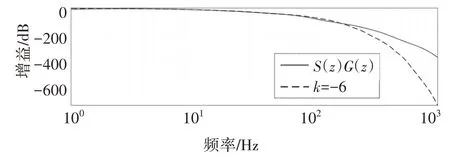
图10 zk与S（z）G（z）的相频特性Fig.10 Phase frequency characteristics of S（z）G（z）and zk

重复控制器的增益Kr（0＜Kr＜1）对系统的稳定性和响应速度非常重要，Kr的取值和稳定裕度成反比，稳定裕度越大，误差的收敛速度越慢.由式（19）得到重复控制系统的特征方程为：

综上，假如所设计的交流侧电流控制和环流抑制策略都能很好地实现控制目标，根据桥臂电压的表达式，结合内环双矢量交流侧电流控制器输出得到的内部电动势指令值ej_ref，和环流抑制输出得到的内部不平衡电压参考值udiffj_ref，从而得到上桥臂和下桥臂电压的指令值分别为：

桥臂电压的参考值经归一化后可作为MMC 的调制波，最终转换为MMC 桥臂子模块的开关信号，外环控制结构与正常工况下保持一致，从而得到不对称工况下MMC的整体控制框图如图11所示.

图11 不对称工况下MMC控制结构Fig.11 MMC control structure under asymmetric condition

4 仿真分析

为了验证所提交流侧电流和桥臂环流优化控制策略的有效性，在MATLAB∕Simulink 软件中搭建了双端51 电平MMC-HVDC 输电系统仿真模型，分别在整流站和逆变站模拟交流侧不对称工况.仿真平台的主要参数如表1所示.

表1 仿真平台主要参数Tab.1 Main parameters of simulation platform

MMC-HVDC 系统一开始处于稳定运行状态，在1.4 s时定电压换流站PCC点a相电压跌落30%.阀侧三相线电压仿真结果如图12 所示，跌落持续0.2 s 后切除，此时交流侧电流的控制目标为抑制负序电流.

图12 阀侧三相线电压仿真结果Fig.12 Simulation results of valve side three-phase line voltage

为了更好地验证本文所提优化策略的优越性能，选取不对称工况下的常规策略作为对比仿真对象，采用SSRF-PLL 和直接抑制负序电流法.仿真结果分别如图13和图14所示.

由图13（a）（b）和图14（a）（b）可知，在正常工况下DSOGI-PLL 和SSRF-PLL 都能实现对正负序分量的精确提取，而在网压不平衡时间段，DSOGI-PLL仿真结果中二倍频交流分量更小，提取结果精度更高，能实现对电压电流交流量的无静差跟踪.

由图13（c）（d）（e）和图14（c）（d）（e）可以发现，本文所提优化控制策略和常规策略都能使三相电流保持平衡，但常规策略下交流侧电流的幅值有所增大；在不对称工况下，电压的不对称使得交流侧瞬时有功功率和无功功率发生波动，导致本文所提优化策略下超调量明显更小；同时，由于交流侧电流增大，桥臂电流增大，使得a 相桥臂子模块中电容电压的波动也相应增大，但常规策略下子模块电容电压的幅值却发生了大幅度跌落.

图13 常规控制策略的仿真结果Fig.13 Simulation results of conventional control strategy

图14 本文所提优化策略仿真结果Fig.14 Simulation results of the proposed optimization strategy

由图13（f）和图14（f）可知，环流中的二倍频分量得到了有效抑制，三相桥臂环流中的直流分量在正常工况下相等，而在故障期间三相桥臂环流中的直流分量幅值不相等，这和理论分析的结果相同.

由上可知，本文采用的优化策略在不对称工况下展现出更好的动态性能和系统优越性.

5 结论

本文通过分析与仿真得到的结论如下：

1）基于双二阶广义积分器的锁相环在故障情况下能够准确提取电压的相位和频率信息，保证了电压电流正负序dq轴分量的提取精度，采用双矢量电流控制器能够有效控制正负序电流，实现三相电流平衡.

2）由PI控制器和重复控制器串联组成的嵌入式重复控制器能够有效跟踪桥臂环流的直流参考值，也能够抑制环流中的谐波，并且在不对称工况期间使三相桥臂环流中的直流分量不相等.

3）由仿真结果可以说明，嵌入式重复控制器能兼顾PI控制器的快速响应和重复控制器的谐波抑制能力，在工程领域具有应用价值.