模块化多电平矩阵变换器的电容电压平衡策略
吴 争,刘 健,杨晓梅,吉 宇,徐晓轶,姚文熙
(1.国网江苏省电力有限公司,南京 210029;2.浙江大学电气工程学院,杭州 310027)
随着电力电子技术和控制技术的飞速发展,高压大功率设备正在得到越来越广泛的应用。由于低电压应力、低谐波含量等特性,多电平拓扑已经成为解决高压功率问题的有效和主要手段[1]。其中,模块化多电平变换器MMC(modular multilevel converter)拓扑族可以通过扩展或者调整级联模块的数目来适应不同的电压等级,表现出良好的可扩展性和冗余备份能力,因而备受学术界和工业界的青睐[2-3]。
模块化多电平矩阵变换器M3C(modular multilevel matrix converter)最早由科罗拉多大学的Erickson 和Al-Naseem 于2001 年提出,用于代替传统的矩阵变换器,提高电压传输比[4]。随后文献[5]提出在M3C 桥臂上串入电感,将其视作电流源处理,从而避免了桥臂短路的问题。M3C 是一个直接AC/AC变换器,在实现能量双向流动的同时,能够实现输入侧任意功率因数以及输入、输出宽范围可调的升降压比[6-7],在大功率和中高压系统有着广阔的应用前景。与背靠背的MMC 相比,M3C 省去了中间直流环节,减少了直流电容,可靠性和效率更高[8-9]。此外,也有学者将M3C 应用到海上风电传输以及分频输电领域[10-11]。
与MMC 类似,模块直流侧的悬浮电容电压保持在给定值是系统稳定工作的前提。M3C 的系统结构比较复杂,桥臂数目众多,且由于输入输出均为交流,桥臂电压和桥臂电流均含有多种频率分量,直接控制9 个桥臂的电容电压与桥臂电流的难度较大[12]。近年来已有多篇文献研究了M3C 的数学模型,实现其输入、输出的解耦控制。其中以文献[13-15]提出的双αβ0 变换法最为典型,该方法能够实现交流侧的解耦控制,但是对于直流侧的电容电压平衡控制主要使用交流环流控制。由于受到电容电压纹波的影响,交流环流控制器的设计难度很大,因而大都使用比例控制,但难以保证电容电压的无静差平衡控制。另外,已有文献对于解耦坐标系下各控制量的物理意义没有做出详细的解释。
借鉴双αβ0 变换法的思想,本文给出了交流和直流侧的等效解耦电路模型,并阐述了各功率环流分量的物理意义。相比直接桥臂电流的控制模型,该模型分离了耦合的桥臂电流分量,避免了电流环相互之间的影响。基于该模型,本文对M3C 的电容电压平衡策略进行改进,通过坐标变化将交流环流转换为直流量来控制,以增强控制的准确性和响应速度。最后,通过搭建仿真模型和实验样机对所提算法的有效性进行验证。
1 M3C 的工作原理
1.1 交流侧解耦模型
M3C 的拓扑结构如图1 所示,每个桥臂由N个H 桥以及一个桥臂电感Lb串联而成,两端分别连接着输入三相系统vs和输出三相系统vm。连接到同一个输入或者输出节点的3 个桥臂称为一个子变换器,因此从输出端口看,M3C 由3 个变换器a、b、c 组成。

图1 M3C 的拓扑结构Fig.1 Topology structure of M3C
如忽略三相中心点的共模电压,根据9 个桥臂的基尔霍夫电压方程可以得到uvw-abc 坐标系下的矩阵表达式为

式中:vsx(x=u,v,w)为输入系统vs的三相电压;(x=u,v,w;y=a,b,c)为桥臂xy 级联H 桥两端的电压;为流过该桥臂的电流;vmy(y=a,b,c)为输出系统vm的三相电压。与所有变换器类似,M3C 的控制目标是系统输入侧与输出侧的电压或电流跟踪参考值,但直接控制量是9 个桥臂的电压和电流。因此需要一个变换矩阵将桥臂分量与输入输出分量对应起来,该过程称为解耦变换。类比αβ0变换实现一个三相系统的解耦,上述方程可以使用双αβ0 变换Cdouble_αβ0(H3×3)实现两个三相系统的解耦[13-15],其中(H3×3)表示4 个3×3 的矩阵。该过程表示为

将该变换应用到式(1)有

式中:vsα、vsβ、vs0和vmα、vmβ、vm0分别为输入三相系统vs和输出三相系统vm的电压在αβ0 坐标系的分量;isα、isβ和imα、imβ分别为输入和输出三相电流在αβ0 坐标系的分量;为9 个桥臂电流的独立环流;为9 个桥臂电压变换后的独立分量。经过变换之后,式(3)实现了电流状态方程的解耦。M3C 的等效模型如图2 所示,可以拆分为输入、输出和环流三部分,有利于各个部分的独立控制。假设三相输入和输出系统中共模分量为0,即vso=vmo=0。输入和输出的中心点O、N 之间没有电流回路,即=0。观察式(3)的桥臂电流项发现,经过解耦后,M3C 存在4 个独立的不影响输入和输出的环流,这些环流在系统内部流动,形成桥臂间的能量交换,可以用作电容电压平衡控制的自由度。

图2 M3C 的等效解耦模型Fig.2 Equivalent decoupling model of M3C
1.2 电容电压平衡控制模型
M3C 交流侧模型能够实现系统的输入输出电能变换要求,而直流侧电容电压的稳定则是整个系统正常工作的前提。实际应用中由于各个桥臂的参数不尽相同,且有死区等非线性因素的存在,桥臂功率不完全对称,从而影响桥臂之间的电容电压平衡。因此需要分析系统的直流侧方程,寻找可以用来控制电容电压平衡的变量。类似(1)式写出桥臂直流电容电压与桥臂功率之间的关系



式(6)对应的功率流向图如图3 所示。

图3 的功率流向图Fig.3 Power flow chart of
依此类推,可以得到各功率环流在每个桥臂上的分布。
2 电容电压平衡策略
2.1 整体控制
系统的整体控制框图如图4 所示,为了简化符号表示,图中将多个变量的上下标合并表示为一组变量,如表示9 个桥臂的电容电压。

图4 系统整体控制框图Fig.4 Overall control block diagram of system
与普通变换器类似,M3C 同样采用电压外环电流内环的控制结构。其中电压外环包括输入侧、输出侧和平衡控制3 个部分,其中:输入侧的电压外环是总电容电压的闭环控制,可以看作是对整个系统的能量补充;输出控制则与三相逆变器的控制方法相同,电压外环的给定根据负载类型确定;而平衡控制则负责桥臂间电容电压的平衡,通过注入特定频率的环流得到需要的桥臂功率,进而控制9 个桥臂之间的电容电压保持稳定,即根据电容电压的不平衡量产生4 个内部环流的给定值,并作为下一级电流环的输入。电流环控制框图如图5 所示,在分别对输入电流、输出电流以及4 个环流控制之后得到桥臂电压在解耦坐标系下的给定,将其做反变换即可得到桥臂xy 电压的给定值,该给定值经过桥臂内的均压和调制后产生PWM 信号。

图5 电流环控制框图Fig.5 Control block diagram of current loop
2.2 子变换器内和子变换器间的电容电压平衡
已有研究采用桥臂环流的电流作为控制量实现电容电压平衡,但由于桥臂电流中频率含量丰富,提取有功成分困难,设计的控制器性能欠佳。因此本文提出一种用环流功率作为控制量的电容电压平衡策略。由于需要控制的环流功率是直流量,因此可以简化控制器的设计,并提高控制性能。以环流功率为例,采用PI 控制后的表达式为

式中,Kp_vc和Ki_vc为PI 控制器的比例和积分参数。
在解耦坐标系下,电压与电流相乘得到对应的环流功率[17],表达式为

由式(8)可以看出,桥臂功率分为两部分:第一部分是输入输出电压电流的乘积,该部分产生电容电压的纹波,是不可控的;第二部分是输入或输出电压和环流的组合,其中特定频率的环流可以产生直流量(有功功率),可用于补偿相应的电容电压直流偏置,是可控的。
假定输入和输出电压和电流定义为

式中:VS和VM分别为输入和输出的相电压幅值;θs和θm分别为输入和输出电压的相位。
选择输入频率环流进行子变换器内部的电压平衡也就是选择式(9)的中间项进行控制,此时控制量可表示为

同理可以获得

结合式(10)和式(11)得到电流控制量为

为了避免电容电压纹波对控制结果的影响,从式(7)中提取电容电压直流量作为电压控制环的输入,以防止电流控制环振荡。同理可以得到平衡其他6 个电容电压量需要的环流,详细过程可以参考文献[16-17],汇总得到桥臂电容电压平衡控制框图如图6 所示。

图6 桥臂电容电压平衡控制框图Fig.6 Control block diagram of arm capacitor voltage balancing
3 仿真和实验验证
为验证所提出的无静差电容电压平衡策略的有效性,本文首先搭建了基于Matlab 的M3C 系统仿真模型。具体仿真参数如表1。系统稳态运行仿真波形如图7 所示。

表1 仿真主电路参数Tab.1 Main circuit parameters for simulation
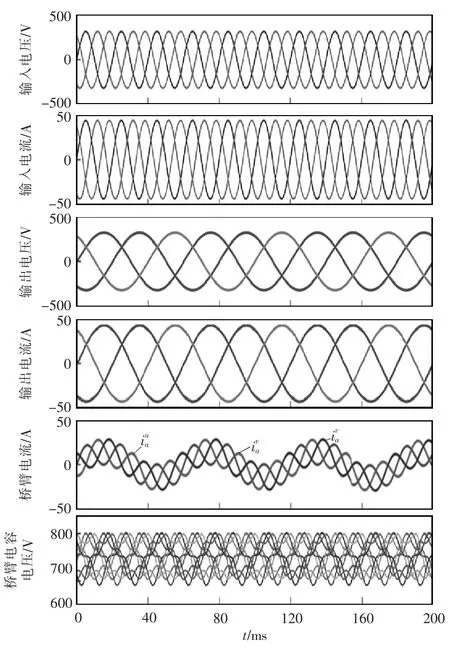
图7 系统稳态运行的仿真波形Fig.7 Simulation waveforms of system under steadystate operation
为了进一步验证基于电压平衡的控制效果,在t=0.5 s 时撤去电容电压平衡控制环(仍然保留总电容控制),桥臂间电容电压平衡控制的仿真波形如图8 所示,可以看到环流给定变成0,电容电压开始发散,系统趋向不稳定。然后在t=0.9 s 重新加入平衡控制,环流给定发生突变电容电压迅速收敛,充分说明该控制的效果良好。

图8 桥臂间电容电压平衡控制的仿真波形Fig.8 Simulation waveforms under arm capacitor voltage balancing control
根据所提出的控制策略,研制了3 kW 的实验样机,输入输出电压的幅值和频率与仿真参数相同。系统稳态运行实验波形如图9 所示,桥臂电压的7 电平波形可以说明3 个串联模块,实验结果与仿真基本一致,也表明了控制器的有效性。


图9 系统稳态运行的实验波形Fig.9 Experimental waveforms of system under steadystate operation
4 结语
本文以M3C 为研究对象,利用解耦变换构建了M3C 输入侧、输出侧、环流的解耦模型。考虑到桥臂环流为多个频率组合的交流电流,提出通过提取环流中的有功电流成分,将其变换成直流量进行功率环流控制的方法,并阐述了如何利用环流实现9 个桥臂的电容电压无静差控制,从而保证系统的稳定可靠运行。根据撤去和加入平衡控制的仿真结果可以看出,该控制方法有效,样机实验系统的稳定运行也证明了本文控制策略的可行性。

