圆环薄膜型介电弹性体换能器发电量影响因素研究

李宝权，陈 洁，崔春华，孙 明，任贯华

（新疆大学电气工程学院，乌鲁木齐 830047）

介电弹性体是一种新型的柔性智能材料，与风能、水能、潮汐能相结合，可以作为一种新的电能量收集方法。基于介电弹性体材料的电能量收集具有绿色环保、灵活多样、成本低、可再生的特点，国内外对于介电弹性体材料能量回收系统开展了大量研究，其中，McKay T 等[1-2]通过介电弹性体发电仿真得到薄膜变形与其电容之间的关系，设计了用于介电弹性体薄膜发电过程的自充电电路；Brochu P等[3]通过研究表明介电弹性体发电效率受到薄膜材料的介电常数、低初始偏置电压等因素影响；朱银龙等[4-6]建立了介电弹性体换能器的数学模型，通过试验验证确定选择恒电荷工作形式最佳，初始电压和拉伸位移是影响发电量、能量转换效率的关键因素。但是都未指出各因素对介电弹性体材料发电量影响的程度。

本文通过分析介电弹性体材料发电机理，对介电弹性体圆环薄膜型换能器的数学模型进行分析，在理想条件下，确定影响介电弹性体换能器发电量的因素，并且通过初步试验确定各因素对发电量影响的规律，最后设计正交试验，确定主要、次要影响因素，进而优化圆环薄膜型介电弹性体换能器，提高其发电量。研究结果为未来设计介电弹性体换能器以及提高介电弹性体材料发电量提供了可靠的参考依据。

1 介电弹性体材料发电机理

介电弹性体材料电能量收集是将机械能转换成电能的循环过程，其实质上是通过控制介电弹性体有序形变从而实现周期循环过程。在进入操作循环之前，通常先将介电弹性体薄膜预拉伸至一定比例长度。介电弹性体薄膜本身是一种绝缘体，在其两面喷涂可随膜变化的柔性电极涂层，膜的表面柔性电极涂层相当于电容极板，此时它的基本功能相当于一个可变电容。介电弹性体材料能量收集过程，在一个循环周期内通常可以简单地划分为4 个步骤[7]，介电弹性体能量收集过程原理如图1 所示。

图1 介电弹性体能量收集过程原理Fig.1 Schematic of energy harvesting process of dielectric elastomer

步骤1拉伸阶段（状态a～状态b），介电弹性体膜通过一定的外力F 拉伸到一定位置，将机械能转换成介电弹性体材料的弹性势能。

步骤2充电阶段（状态b～状态c），此阶段在介电弹性体膜两侧的柔性电极施加直流偏置电压Uin进行充电，两侧柔性电极积累大量异性电荷，使结构具有初始电势能。

步骤3恢复阶段（状态c～状态d），撤去外力F，介电弹性体膜在弹性回复力的作用下回缩到初始形状或预拉伸状态，此过程中材料弹性势能克服静电力做功，使得薄膜同侧电极上的同性电荷之间距离缩小，异侧电极上的异性电荷之间距离增加，从而使得电势能增加，将输入的机械能转换为电能。

步骤4放电阶段（状态d～状态a），移除电荷并使膜完全恢复到其初始工作状态。

由以上描述及图1 可知，这种结构类似于传统的电容器，其中电容容量C 取决于面积S 和厚度d，其表达式为

式中：εr为材料的相对介电常数；ε0为真空介电常数，约为8.85×10-12F/m。

本文采用恒电荷工作方式，可得

式中：Q 为电容电荷量；C0为未发生形变时的电容容量；Uo为一个循环周期输出电压；C1为拉伸产生形变最大值时的电容容量；Ui为所施加偏置电压。介电弹性体换能器在一个循环周期所收集能量ΔW[8]为

2 介电弹性体换能器结构数学模型

相比于单轴拉伸、纯剪切变形[9]，等双轴拉伸是最优的拉伸形式。故本文介电弹性体换能器采用圆环薄膜型结构[4]，其换能器模型示意如图2 所示。

图2 圆环薄膜型结构的换能器模型示意Fig.2 Schematic of transducer model with annular thin film structure

因为介电弹性体拉伸前后体积V 保持不变，即

式中：S0为未变形时的面积；d0为未变形时的厚度；Si为拉伸变形后的面积；di为拉伸变形后的厚度。圆环形介电弹性体初始状态未拉伸时的表面积为

式中，R 和r 分别为圆环薄膜型结构的外框内半径和内框半径。当拉伸发生位移y 近似于圆台时，根据圆台侧面积公式，可得此时表面积为

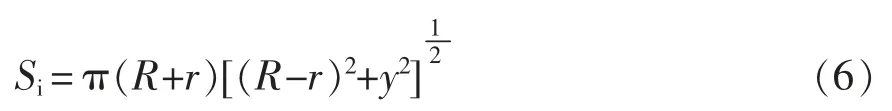
由式（1）与式（6）可得

由式（2）与式（7）可得

由式（3）与式（8）可得

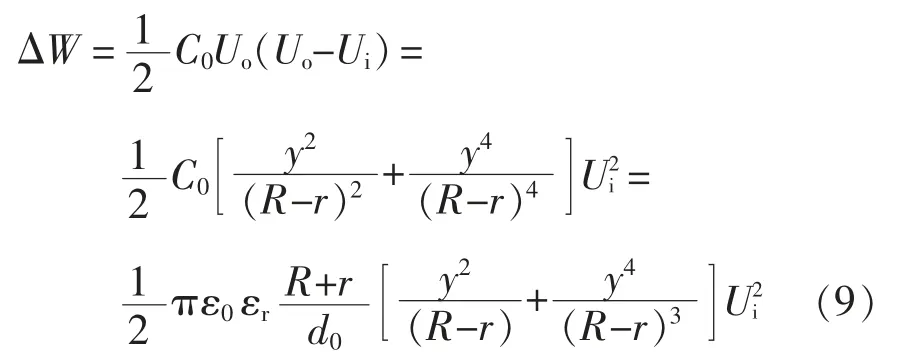
由式（9）可以确定，在恒电荷工作方式且不考虑内部损耗（材料黏滞损耗和电流泄漏等）的情况，介电弹性体换能器的一个循环周期发电量以及材料的6 个因素：相对介电常数、初始电容厚度、固定换能器介电弹性体薄膜的内框半径、外框内半径、拉伸位移及初始施加偏置电压相关。

3 影响因素的试验分析

由式（1）和式（5）可知，在圆环薄膜型结构固定的情况下，即受到制作工艺限制，此时，材料的相对介电常数、初始电容厚度、固定介电弹性体薄膜的内框半径和外框内半径都为固定值，则初始电容C0为常数。又由式（9）知，当内框半径、外框内半径和初始电容皆为常数时，发电量只与拉伸位移、施加的偏置电压有关。此时对式（9）求导可得

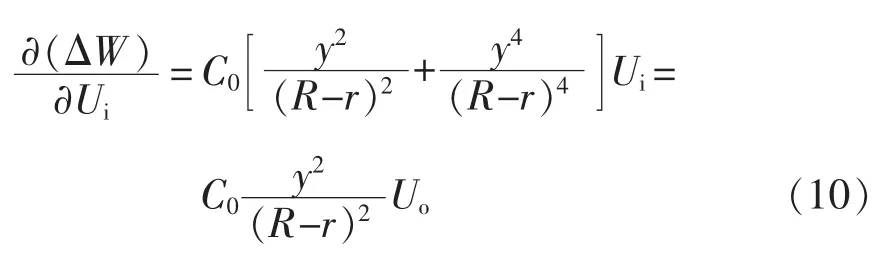
可见，在圆环薄膜型结构固定的情况下，发电量的变化率只与施加偏置电压和拉伸位移有关。因此研究在圆环薄膜型结构固定的情况下，所施加偏置电压、拉伸位移以及输出电压对发电量的影响。其发电量通过测量输入电压、输出电压及始末电容由式（3）计算得到。

3.1 主要试验材料与仪器

试验仪器有示波器（TBS 1052B-EDU）、万用表（VICTOR VC890D）、高压发生器、电容表及模拟电路试验箱（THM-1 型），试验材料及试剂有聚丙烯酸橡胶（3 M，VHB4910 型）、导电膏（DDG-A 型）、石墨粉、SYLGARD184 硅胶、硅油和正庚烷。

3.2 介电弹性体换能器尺寸

本次试验采用预拉伸率为2×2，即在制作换能器时，预先将介电弹性体材料在x、y 两个方向拉伸为原长度的2 倍，内框半径r=75 mm 与外框内半径R 分别按比例1∶1.3、1∶1.6、1∶2.0 设计，薄膜厚度d0为0.25 mm。

3.3 试验过程及结果

为了测量各因素对介电弹性体换能器发电量的影响，需要对介电弹性体换能器进行充电和放电，并对其输入和输出电压进行测量，采用如图3所示的电能量收集电路[3]。在此试验中，将介电弹性体换能器收集电能的4 个形变状态定义为状态a、b、c、d，其中，状态a 为介电弹性体换能器未拉伸前的初始状态，状态b 为介电弹性体换能器的最大拉伸变形状态，状态c 为介电弹性体换能器最大拉伸下的充电状态，状态d 为介电弹性体换能器回弹后的形变状态。对应于由这4 个形变状态顺次构成的工作循环周期过程，通过控制图3 所示的电能量收集电路中两个开关S1、S2的协同动作，可测量介电弹性体换能器在恢复阶段的电压[10]。电路工作状态示意如图4 所示。

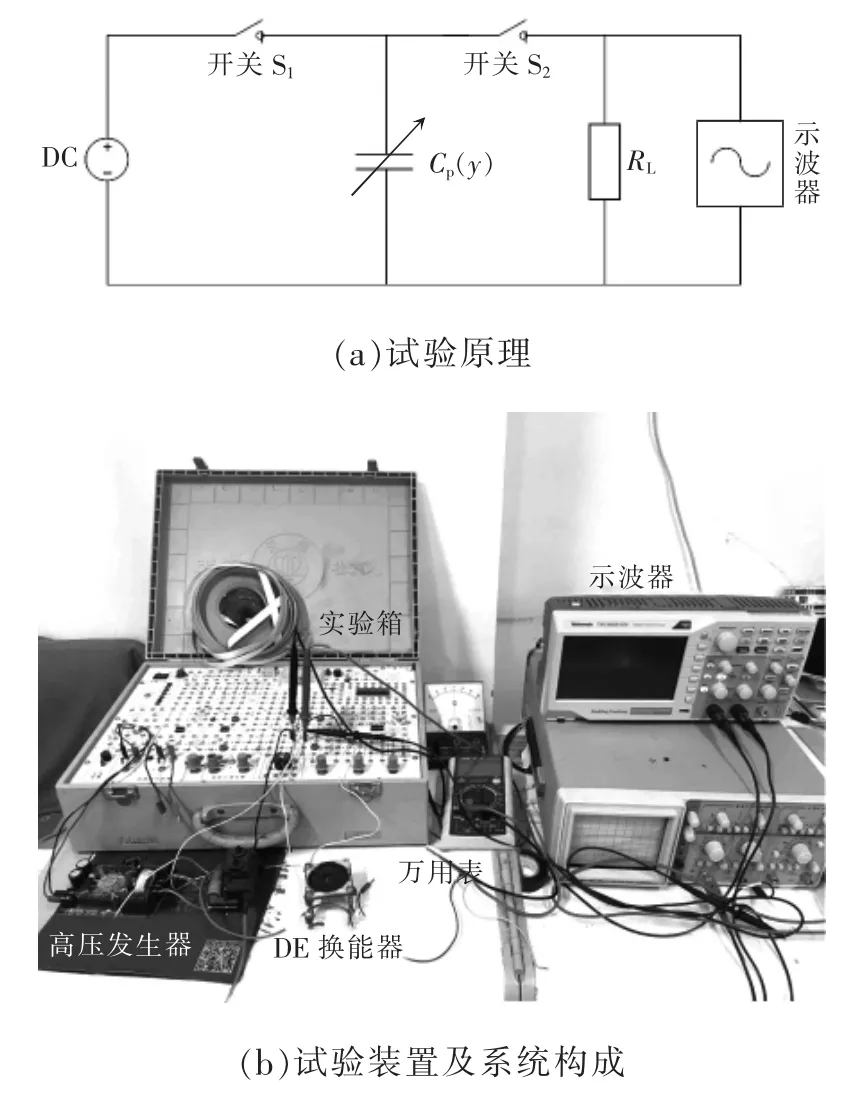
图3 电能量收集电路Fig.3 Electrical energy harvesting circuit

图4 电路工作状态示意Fig.4 Schematic of the working state of circuit

本次试验中偏置电压为400、600、800、1 000 V，拉伸位移分别取40、60、80 mm，测量不同参数下输出的电压，取3 次测量结果求平均值。

在采用柔性电极为石墨粉以及固定介电弹性体薄膜的内框半径与外框内半径比例不同的条件下，得到输出电压试验结果如图5 所示。由试验结果可以得出以下结论：

图5 输出电压试验结果Fig.5 Test results of output voltage

（1）在固定介电弹性体薄膜的内框半径和外框内半径比例、拉伸位移一定时，输出电压随偏置电压呈线性输出，这与理论分析基本一致。可见，影响因素之间存在相互作用，从而进一步影响发电量。

（2）在固定介电弹性体薄膜的内框半径和外框内半径比例、偏置电压一定时，输出电压随着拉伸位移的增加而增大，这是因为拉伸位移不断增加，使得介电弹性体换能器材料面积变大，厚度变薄，导致电容容量变大，使得输出电压增大，进而使得发电量增加。

（3）在固定介电弹性体薄膜的内框半径和外框内半径比例一定时，相比于拉伸位移，偏置电压对输出电压增大的变化率影响程度大一些。

（4）在固定介电弹性体薄膜的内框半径和外框内半径比例、偏置电压一定时，在拉伸位移超过60 mm 后曲线斜率几乎无变化，输出电压开始几乎不变。这是因为随着拉伸位移的不断增加，介电弹性体膜表面的柔性电极开始出现裂纹，随着裂纹的出现，换能器储存电荷的能力开始下降，致使输出电压不变甚至降低，进而影响发电量减少。

4 正交试验分析

通过初步对数学模型分析和试验验证，可知在恒电荷工作方式下影响介电弹性体换能器的发电量的6 个因素。在柔性电极材料石墨粉确定、圆环型薄膜结构固定的情况下，从第3.3 节试验结果可以看出圆环薄膜型换能器发电量与施加偏置电压和拉伸位移有关。但第3.3 节仍不能确定各因素对介电弹性体换能器的发电量影响程度，由于影响因素较多，且各影响因素存在相互作用，如果逐个方案试验，则试验次数较多，数据处理复杂。

故采用正交试验设计[11-14]，该方法是使用一种规范化表格（正交表）进行试验设计，可以用代表性较强较小的试验次数，研究各个因素对试验指标的影响，确定因素影响的主次顺序，取得最佳参数组合。

4.1 试验因子的分析选择

正交试验的首要步骤是对试验因子进行确定，尽可能全面地列出影响因素，避免出现遗漏重要的影响因素。通过第3.3 节以及对式（4）、式（5）分析可知，在圆环薄膜型结构固定的情况下，d0为常数，在试验时不予以考虑其影响；除此之外，仍有5 个因素对介电弹性体换能器发电量有较重大的影响，为简化数据处理（不影响试验结果），将其进行简化为4 个因素，其中将材料的固定换能器介电弹性体薄膜的内框半径r 和外框内半径R 两者比例定为1 个正交试验因子，而拉伸位移y、初始施加偏置电压Ui以及电极材料种类（影响εr大小）为另外3 个正交试验因子，并对这些试验因子分别编号为A、B、C、D。

4.2 试验因子水平确定

确定了正交试验的试验因子后，各因子的水平选取也很重要，会直接影响到试验效果。为了能够合理地进行试验，体现试验因子对介电弹性体换能器的影响，同时还要尽可能地降低试验成本，需要从水平确定上加以平衡。本文正交试验的试验因子水平选定为3。

IBM SPSS Statistics 是一款统计分析软件，其SPSS Base 模块提供了从简单统计描述到复杂多因素统计分析方法。本文采用IBM SPSS Statistics 25 软件，先生成介电弹性体换能器正交试验因子与水平的表，见表1，然后再生成正交配置试验表格，L9（34）正交试验表见表2。

表1 介电弹性体换能器正交试验因子与水平的表Tab.1 Table of orthogonal test factors and levels for dielectric elastomer transducer

表2 正交试验表Tab.2 Orthogonal test table

4.3 试验结果与分析

根据正交配置试验表进行试验，正交试验结果及极差分析如表3 所示。采用极差分析法与方差分析法分别对试验结果进行分析，考察各因素对介电弹性体换能器发电量影响。

表3 正交试验结果及极差分析Tab.3 Orthogonal test results and range analysis

4.3.1 极差分析法

极差分析是通过计算每个因子水平对应的试验指标平均值的最大值与最小值之差（即极差），说明该因子对试验指标的影响，计算公式为

图6 试验因子与介电弹性体换能器发电量关系Fig.6 Relationship between test factors and power generation of dielectric elastomer transducer

根据正交表的综合可比性，由上述计算结果及趋势分析可得出以下结论：

（1）在本试验中，介电弹性体换能器发电量Ri最大的试验条件为：换能器介电弹性体薄膜的内框半径和外框内半径比例为1∶2.0，拉伸位移为60 mm，初始施加偏置电压为1 000 V，电极材料种类选用石墨粉，即最佳组合试验条件为A3B2C3D1。

（2）在此最佳组合试验条件下，再次试验，最后测量此时输出电压为1 677 V，计算得出一个循环周期发电量为4.38 mJ，高于本次正交试验条件下一个循环周期最大发电量3.23 mJ，提高了36%，证明了正交试验能够优化圆环型介电弹性体换能器，使得发电量进一步提高。

4.3.2 方差分析法

极差分析法虽然简单易行，却不能区别试验条件改变引起的数据波动与试验误差引起数据波动。为了弥补这种不足，应对正交试验结果进行方差分析[11，15-18]。根据F 及给定的显著度a，可判断各因素对试验指标的影响相对于试验误差对试验指标的影响是否显著。由IBM SPSS Statistics 25 软件对数据进行线性分析操作，进行主体间效应检验，其因变量为发电量，生成方差分析表（ɑ=0.05），见表4。

表4 正交试验方差分析Tab.4 Orthogonal test variance analysis

从表4 中可看出，通过观察F 和显著性的值，可以确定因子A、C、D 显著（ɑi<ɑ=0.05），因子B 较显著（ɑ=0.05<ɑi<0.10）。可以归纳出因子影响的主次顺序为A、C、D、B。

综合正交试验极差分析法和方差分析法可知，对介电弹性体换能器发电量影响因素主次顺序为：固定换能器介电弹性体薄膜内框半径和外框内半径长度比例、初始施加偏置电压、柔性电极材料种类、拉伸位移。该研究结果对未来介电弹性体换能器设计以及提高介电弹性体材料发电量提供了可靠的参考依据。

5 结论

本文通过理论分析和设计正交试验，研究了圆环型介电弹性体换能器发电量影响因素，得到如下结论：

（1）在恒电荷工作方式下，不考虑内部损耗的情况下，确定了影响圆环薄膜型介电弹性体换能器发电量的因素分别为：材料的相对介电常数、初始电容厚度、固定换能器介电弹性体薄膜的内框半径、外框内半径、拉伸位移及初始施加偏置电压。

（2）在确定各因素对发电量影响规律的情况下，设计正交试验，在最佳组合试验条件下，圆环薄膜型介电弹性体换能器发电量进一步提高，证明了可以利用正交试验方法对圆环型介电弹性体换能器进行优化，且具有高效性和准确性。

（3）通过设计正交试验方案，确定了介电弹性体换能器发电量影响因素主次顺序为：固定换能器介电弹性体薄膜的内框半径和外框内半径比例、初始施加偏置电压、电极材料种类、拉伸位移。

该正交试验对未来介电弹性体换能器设计以及提高介电弹性体材料发电量提供了可靠的参考依据。后续工作需要进一步研究预拉伸率和拉伸频率等其他因素对圆环型介电弹性体换能器发电量的影响。