基于被动时间反转-卷积神经网络的OFDM 水声通信系统研究

付晓梅，王思宁，胡雅琳

（天津大学海洋科学与技术学院，天津 300072）

水声（Underwater Acoustic，UWA）通信是水下探测和信息获取的重要技术.正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）是一种可实现高速率传输的多载波通信方案［1-2］.然而，水声信道存在显著的多径效应和多普勒效应［3］，造成子载波间的正交性被破坏导致严重的载波间干扰（Inter-Carrier Interference，ICI）和符号间干扰（Inter-Symbol Interference，ISI）.这对OFDM 水声通信系统接收端的信道估计和信号检测带来一定的挑战.

OFDM 水声通信系统接收端信道估计和信号检测方法将直接影响系统的误码率性能.传统估计算法如最小二乘（Least Square，LS）、线性最小均方误差（Linear Minimum Mean Square Error，LMMSE）和正交匹配追踪（Orthogonal Matching Pursuit，OMP）等［4-6］.信号检测主要有最大似然检测（Maximum Likelihood，ML）、迫零检测（Zero Forcing，ZF）和最小均方误差检测（Minimum Mean Square Error，MMSE）等.然而水声信道严重的多径效应使得上述估计和检测方法的效果并不理想.

近年来，针对水声信道的多径效应，有学者提出被动时间反转技术（Passive Time Reversal，PTR）用于处理水声信道特征［7-8］，不需要先验的信道信息，在时间和空间上压缩信号以减轻系统的ISI，受到广泛关注.文献［9］提出了基于单阵元无源时间反转镜的Pattern 时延差编码水声通信系统，在时变、空变的信道中实现低误码率通信.文献［10］将PTR 与自适应信道均衡器级联以去除残余ISI，进一步提高通信系统接收端的性能.文献［11］提出基于PTR的滤波器组多载波水声通信方法，其无须插入导频提高了通信速率.文献［12］将PTR 应用到OFDM 水声通信系统中，并采用加入循环后缀方法对抗系统的ISI 和ICI.

深度学习由于具有强大的学习能力，可被用于水声通信系统的接收端进行信号恢复.文献［13］提出基于深度神经网络（Deep Neural Network，DNN）的OFDM 联合信道估计与信号检测算法，无须明确的信道估计和信号检测，可以直接恢复传输符号.文献［14］利用DNN 代替信道估计模块，其性能优于传统的LS 算法.为了简化接收端设计，文献［15］将OFDM 水声通信系统接收端的解调、信道估计与均衡及星座图解映射用一个DNN 模块代替，提高了系统可靠性.以上文献均将DNN 直接引入OFDM 系统进行信号恢复，相较于传统系统，它能够提升水声通信系统性能.然而，现有的基于深度学习的系统只是把DNN 当作一个“黑匣子”，没有针对水声信道的特性进行设计与优化，训练完成的网络对环境敏感，对不同水声信道的鲁棒性较差.

为了提高OFDM 水声通信系统的接收端性能，本文构造一种新型的被动时间反转-卷积神经网络（Passive Time Reversal-Convolutional Neural Network，PTR-CNN）应用于OFDM 接收端.该方法的主要思想是深度学习联合时间反转理论来对抗系统的ISI 和ICI，从而提升系统性能.针对水声信道的多径效应，首先在接收端利用PTR 削弱信道的多径以减轻系统的ISI，之后利用卷积神经网络（Convolutional Neural Network，CNN）可以有效捕捉时频特征的特点［16-17］，将OFDM 信号的实部和虚部并行化以形成二维矩阵，输入CNN网络中充分挖掘信号特征，处理系统的ICI 和残余ISI，最后网络直接恢复比特流.该方法在具有较强的多径效应和多普勒效应的不同水声信道下测试，与目前主流的接收端信道估计和信号检测算法对比，系统具有更高的可靠性.

1 基于PTR-CNN的OFDM水声通信系统

1.1 系统模型

基于PTR-CNN的OFDM水声通信系统如图1所示.在发送端，随机生成的二进制比特序列bs首先通过正交幅度调制（Quadrature Amplitude Modulation，QAM）映射生成长度为N的符号ds，N代表子载波数；然后将ds转换为并行传输的数据d=（d0，d1，d2，…，dN-1，）T，并利用快速傅里叶逆变换（Inverse Fast Fourier Transform，IFFT）获得时域信号x～(t).信号(t)发送到水声信道的过程公式为：

图1 基于PTR-CNN的OFDM水声通信系统Fig.1 PTR-CNN based on OFDM underwater acoustic communication system

式中：⊗表示卷积运算；h(t)和n(t)分别为时域信道响应和具有零均值的加性高斯白噪声（Additive White Gaussian Noise，AWGN）.

在接收端，考虑到水声信道的强多径和随机多普勒特性，设计基于PTR-CNN 的接收机结构.具体步骤如下：基于PTR 理论削弱信道的多径分量，增强主路径信息能量，进而减轻系统的ISI，使用CNN 处理系统的ICI 和残余ISI；将上述输出的复数信号的实部和虚部并行化为二维矩阵，再输入CNN 中进行训练学习；最终进行回归预测，恢复接收数据流.

1.2 水声信道

水声信道与陆地信道不同，具有时变快、多径强、多普勒频移大等特点，故水声信道存在明显的多径效应和多普勒效应.本文使用Qarabaqi 等［18］提出的基于统计特性的水声信道模型，该模型考虑了声传播的物理特性和随机变化的影响，多径效应和多普勒效应的影响通过传递函数建模如下：

式中：是对所有路径具有滤波器效应的幅度矩阵；p为多径数量；hp(t)和τp(t)=-ap(t)分别为第p径的路径增益系数和时延，属于大尺度参数，它们根据随机多普勒因子ap随时间变化，多普勒因子ap=vp∕c通过收发端的相对运动速度和漂移速度决定水声信道多普勒频移的大小p=1，2，…，表示建模为复高斯过程的散射系数；H(f，t)表示频域中时变信道传递函数的矩阵，在时域中用h(f，t)表示.

2 PTR-CNN网络模型

2.1 PTR-CNN结构

PTR-CNN 网络模型主要包括PTR、数据预处理、卷积层、展平层和全连接层.具体结构如图2所示.

图2 PTR-CNN具体结构图Fig.2 The specific structure of PTR-CNN

PTR-CNN网络的发送信号由探测信号和OFDM信号组成，其中探测信号使用的是自相关特性好的线性调频（Linear Frequency Modulation，LFM）信号，它在接收端同时起到同步和检测作用，由于不需要导频信号，因此PTR 能够提高有效通信速率.PTR 的输入是接收的探测信号和接收的OFDM 信号，然后将时间反转成，并将其与卷积，通过时反信道消除多径的影响.具体公式如下：

式中：n1(t)为噪声干扰的总和；h(t)⊗h(-t)是时反水声信道，是信道冲激响应的自相关函数，可以近似看成δ函数.因此，式（4）可以写成：

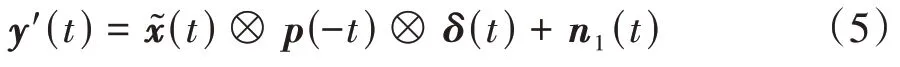
从式（5）可以看出，接收信号通过时反信道可以实现多径聚焦增益，消除大部分ISI，但是这个过程会引入反转后的探测信号.因此，要与探测信号p(t)卷积消除探测信号的影响，其过程如式（6）所示.

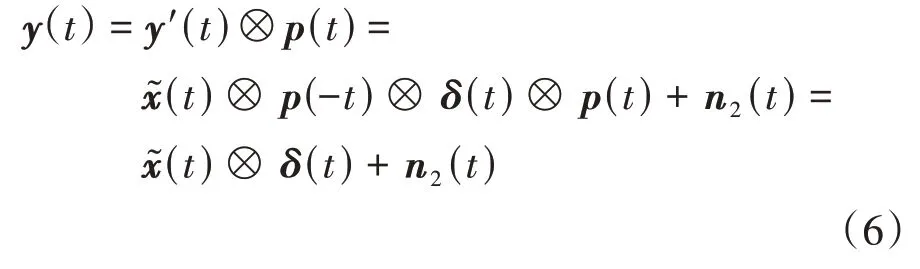
式中：n2(t)为叠加的噪声干扰，包括发送信号、探测信号和环境噪声等.虽然PTR 可以有效地压缩信号减轻ISI，但还是存在残余的ISI、探测信号的自相关干扰、叠加的噪声干扰以及多普勒效应造成的ICI，具体分析在3.2 节介绍.因此，需要通过CNN 进一步处理来提升信号检测性能，从而提高系统的可靠性.

数据预处理是将PTR 输出的结果转换成二维矩阵输入卷积神经网络中进行信道检测，由于y(t)为复数，而神经网络通常以实数作为输入，因此将y(t)的实部和虚部拼接成二维矩阵得到yc∈RH×W.数据预处理维度变化示意图如图3所示.

图3 数据预处理维度变化Fig.3 Dimension change of data preprocessing

将yc送入二维卷积层进行特征提取，在卷积层中，利用卷积核k从上一层的特征图中的局部邻域提取特征.然后，通过滑动卷积核的位置对数据进行卷积求和并且叠加偏置.之后送入非线性激活函数区域进行非线性变换，卷积层的激活函数选择的是缩放指数线性单元（Scaled Exponential Linear Units，SELU）激活函数.

它具有自归一化的特点，其方差稳定性避免了训练过程中的梯度爆炸和梯度消失［19］.将第i卷积层的输出表示为∈RH×W×C（C为输出通道），则第j个特征图中位置为[x，y]的单位值表示如下：

本文设计4个卷积层，卷积核大小均为3×3，均使用SELU 激活函数，通道数除了第4 层外均为16，整个卷积层使用“same”填充，步长设置为1，以保证卷积层中的特征图的大小保持不变且更加精确地提取特征信息.其中，第4层输出通道设置为1，主要用于降维输出，所以最后卷积层的输出为∈RH×W×1，如图2所示.

2.2 训练过程

在搭建好网络模型之后，需要通过训练数据迭代、超参数调试和优化算法来改善神经网络参数，使其达到预期的检测效果.在训练阶段，首先按照具体参数生成随机数据序列作为传输符号，OFDM 水声通信系统的参数如表1 所示.然后基于水声信道的统计特性模拟当前随机训练信道［18］，通过收集当前信道失真（包括信道噪声）、接收信号和估计的信道脉冲响应得到的OFDM 信号作为训练数据，原始的二进制传输数据作为训练标签，训练集和测试集的数量比例为4∶1.其网络参数包括卷积层和全连接层，随着迭代周期的增加，优化器不断更新这些参数，损失函数也随之收敛.在本文中，使用Adam（Adaptive Moment Estimation）优化算法，初始学习率设置为0.001，并使用均方误差（Mean Square Error，MSE）损失函数来最小化网络的输出b^s与训练标签bs之间的差异.公式如下：

表1 OFDM 水声通信系统参数Tab.1 OFDM UWA communication system parameters

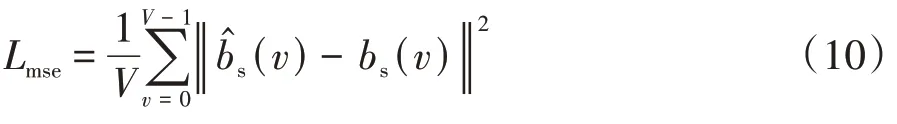
式中：v=0，1，…，V-1，表示批量大小，本文设置为64.当损失函数达到预设阈值时，网络的训练参数停止更新，表示训练阶段结束.在测试阶段，可以直接在接收端加载已完成训练的网络参数，对接收到的信号进行直接检测.

由于声信号在水下传播缓慢，一般在陆地无线通信中多径时延是微秒级，而在水声通信中多径延时是毫秒级，几十甚至是几百毫秒.因此，水声通信传播需要更长的信号符号周期和更小的信号间隔.本文通过增加卷积层层数来匹配水声信道环境，以进一步提升信号检测性能.

3 仿真结果分析

3.1 水声信道环境

针对OFDM 水声通信系统，本文将验证所提出的PTR-CNN 网络模型的性能.水声信道参数如表2所示.模型训练过程仅在环境2 中执行，接收信噪比（Signal-to-Noise Ratio，SNR）设置为20 dB，高信噪比可以得到更加精确的网络输入和特征提取，并且与低信噪相比其泛化能力更强，测试信噪比值在0～20 dB 内，步长为5 dB.为了验证所提方法的鲁棒性和泛化能力，本文模拟4 种不同的水声信道环境（环境1～环境4），它们具有不同的传输距离、时延扩展和多普勒频移.水声信道的时域脉冲响应如图4所示.

表2 水声信道参数Tab.2 Underwater acoustic channel parameters

图4 水声信道的时域脉冲响应Fig.4 Time domain impulse response of underwater acoustic channel

3.2 系统性能分析

在本节中，分析不同水声信道环境（不同的多径效应和多普勒效应）下PTR-CNN 算法与已有的传统算法的性能.图5显示了环境1在经过PTR处理前后的信道状态.由图5 可见，PTR 能够将能量集中在主路径上，削弱其他路径能量，相比于原信道，大大地减少了多径时延，减轻了ISI.但是，还存在部分残余ISI，进而引入CNN 提取信号特征和信道特征，PTRCNN 通过训练提取信号特征，能够处理系统残余ISI，有利于信号恢复.环境1 下不同算法的误码率（Bit Error Rate，BER）曲线如图6 所示.为了更加清晰地展示该算法的性能，仿真中还比较了基于导频的信道估计和信号检测算法，分别是LS和OMP信道估计结合ZF 信号检测算法，其结果也在图6中给出.由图6可知，LS_ZF整体受噪声的影响比较大导致其性能最差，OMP_ZF 由于事先获取信道先验知识进而取得一定的误码率增益，而本文所提的PTR-CNN能很好地结合PTR 和CNN 的优势，获得更优的系统可靠性.

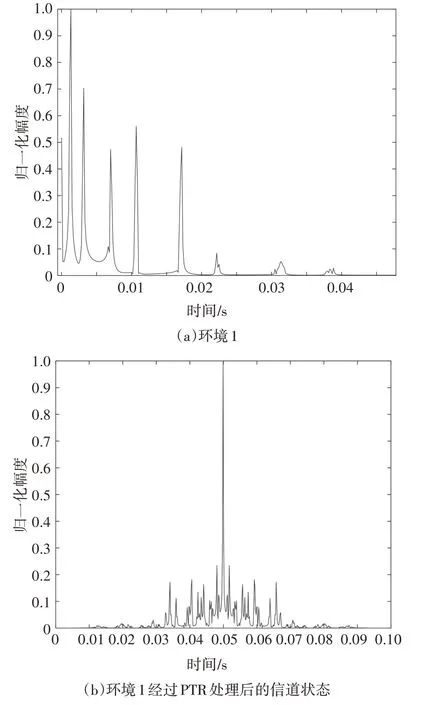
图5 环境1经过PTR处理前后的信道状态Fig.5 The channel state of environment 1 before and after the PTR

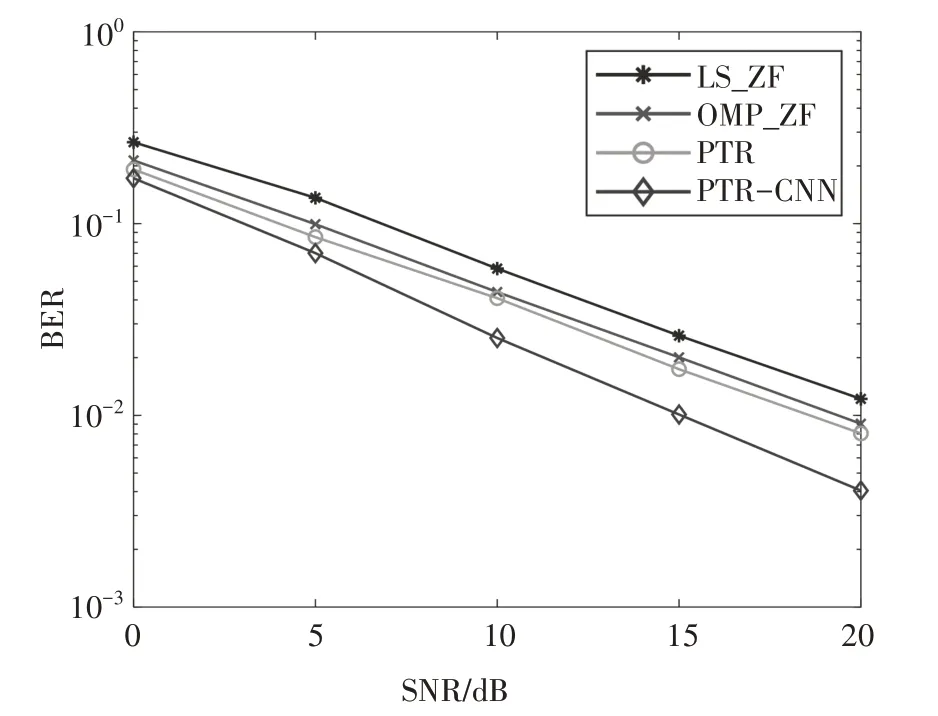
图6 环境1下不同算法的BER曲线Fig.6 BER curves of different algorithms in environment 1

水声信道除了多径效应外，通常还存在多普勒效应，环境2相比于环境1引入了由相对运动引起的随机多普勒频移.环境2 经过PTR 处理前后的信道状态如图7 所示.由图7 可以看出，此时的PTR 无法很好地削弱多径信息，虽然有一个明显的最强主路径，但是其他路径的削弱效果并不太明显，这表示仅仅使用PTR 无法很好地对抗系统的ICI.环境2 下不同算法的BER 曲线如图8 所示.由图8 可知，由于多普勒频移的引入，传统的PTR 算法整体性能比OMP_ZF 算法差，而本文提出的PTR-CNN 明显优于上述方法.在信噪比为20 dB 时，BER 达到10-3数量级，展现了在水声信道中引入CNN 带来的系统性能增益，它能够利用其强大的学习能力优化系统的误码率.

图7 环境2经过PTR处理前后的信道状态Fig.7 The channel state of environment 2 before and after the PTR

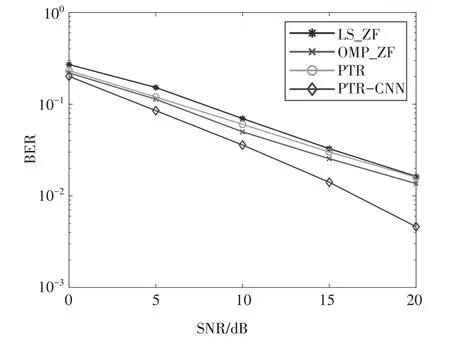
图8 环境2下不同算法的BER曲线Fig.8 BER curves of different algorithms in environment 2

为了进一步探究PTR-CNN 算法的系统性能，图9 对比了PTR-CNN 模型和CNN 模型在不同迭代次数时的BER 曲线，其中CNN 模型的网络输入为接收信号y～ (t)，随着迭代次数的增加，两种网络模型的BER 均有下降.与CNN 相比，PTR-CNN 模型对接收信号做PTR 处理以减小信道特性的影响，并且保持输入数据的同分布会有利于网络的特征提取和快速收敛.在迭代50 次时就可以达到较低的BER，而CNN 模型在迭代50 次时还无法充分地学习，只有不断地增加迭代次数才会进一步下降收敛.本文设计的PTR-CNN 算法能够快速有效地处理系统的ISI 和ICI，同时为了避免过拟合，只迭代训练50 次就保存模型，大大减小了训练开销.

图9 不同算法在不同迭代次数时的BER曲线Fig.9 BER curves of different algorithms at different iterations

3.3 鲁棒性分析

图10为不同循环前缀长度时BER曲线.从图10可以看出，对于传统的PTR 算法，为了更好地实现信道聚焦，需要一定的循环前缀抵抗ISI，所以循环前缀长度的减少导致误码率性能严重下降.而PTRCNN 算法对循环前缀长度不敏感，这得益于神经网络强大的学习能力，网络经过数据集学习使得它对不同的循环前缀长度具有较强的鲁棒性，可以不需要增加循环前缀来抵抗系统的ISI，可以进一步提高基于PTR-CNN的OFDM水声通信系统的频谱效率.

图10 不同循环前缀长度时BER曲线Fig.10 BER curves of different cyclic prefix lengths

图11 为PTR-CNN 算法和传统PTR 算法在不同信道环境下的BER 曲线.PTR 算法严重依赖于当前的信道条件，且多普勒频移会影响信道的多径聚焦增益，其误码率随着信道环境变得恶劣而严重下降.相比之下，PTR-CNN 算法能够在较强的多径效应和多普勒效应下对抗系统的ICI 和ISI，进一步提升系统的信号检测性能，在不同测试环境下展现了良好的鲁棒性.当测试环境与训练环境相同时，即以测试环境为环境2 的BER 曲线为基准，当信噪比小于10 dB 时，测试环境为环境3 和环境4 的BER 几乎不受影响；当信噪比为20 dB 时，它们相比于环境2 分别损失约1 dB 和2 dB 的增益，但整体仍优于传统的算法.这表明PTR-CNN 网络可以容忍一定程度的时延扩展和多普勒频移，基于PTR-CNN 的OFDM 水声通信系统适用于具有ISI∕ICI的水声信道.

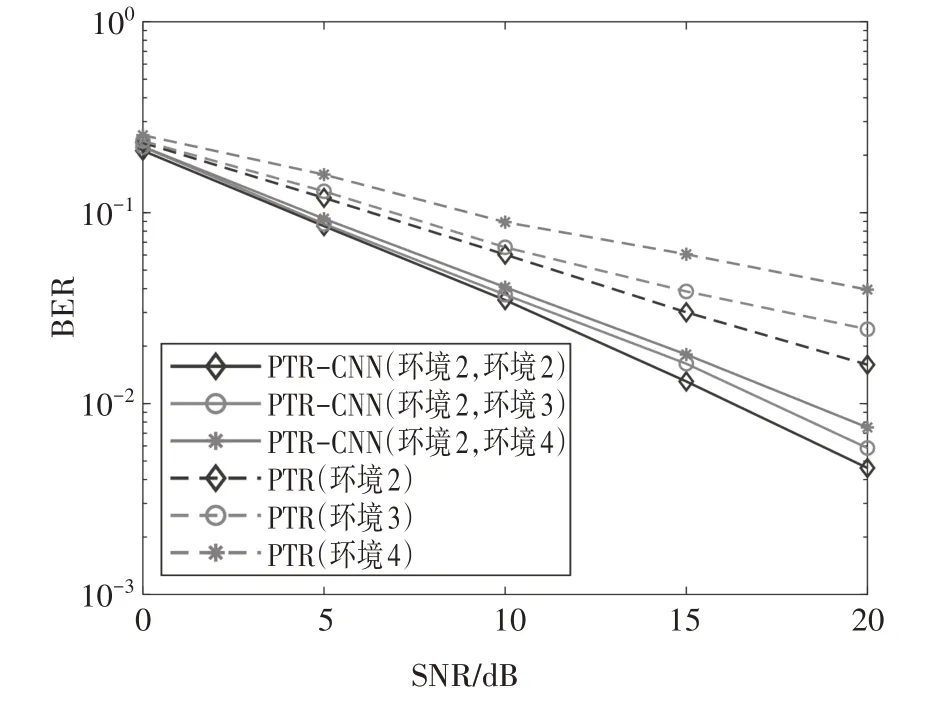
图11 不同算法在不同信道环境下的BER曲线Fig.11 BER curves of different algorithms in different channel environments

图12 比较了5 层DNN 模型［15］和PTR-CNN 模型对于水声信道环境的鲁棒性，DNN 模型同样在环境2 下训练，在环境2～环境4 中进行测试.文献［15］中使用5 层全连接层，在系统的载波数和ICI 更大的情况下，没有针对水声信道的特性进行预处理，大大增加了网络的权重参数且不能很好地学习更加复杂的信道特性.而对于PTR-CNN 模型，在模型训练前针对信道特性做了初步处理，同时卷积层能够通过层间的权重共享减少网络的权重参数.由图12 可以看出，DNN 和PTR-CNN 网络模型对环境的鲁棒性不同，DNN 模型在测试环境为环境3 和环境4 的BER相比于测试环境为环境2 时有较大幅度的变化；这说明DNN 模型对环境的变化比较敏感，随着信噪比的增加，误码率不能大幅降低，此时，DNN模型几乎完全失效.而PTR-CNN模型对环境的变化不敏感，在测试环境为环境3 和环境4 的BER 与DNN 模型在测试环境为环境2 的BER 基本相同，这表明PTR-CNN 网络模型对于不同的水声信道的环境鲁棒性较强.

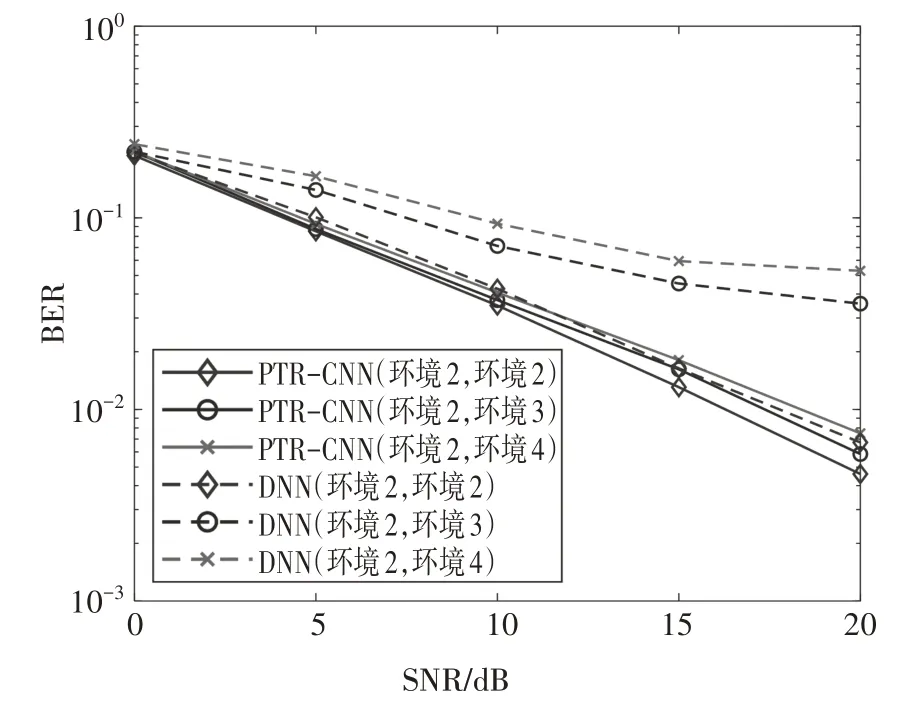
图12 不同网络模型在不同信道环境下的BER曲线Fig.12 BER curves of different network models in different channel environments

4 试验结果分析

为了分析PTR-CNN 网络模型在实际水声通信系统中的误码率，本研究团队于2020 年9 月在天津海河进行了水声通信试验.试验地点的水深约8 m，发送换能器深度约1.5 m，接收水听器深度约1.5 m.在试验过程中，使用在河面上漂流的船只携带发射换能器和接收水听器，试验中船只以0.5 m∕s 的相对运动速度漂移.试验通信距离分别约为500 m和1 000 m.

试验中所用的系统参数与仿真参数相同，载波频率为25 kHz，带宽为22～28 kHz，采样率为96 kHz.发送数据如图13（a）所示，由LFM、间隔和OFDM 数据符号组成，LFM 符号用于帧同步和探测信号，一帧传输3个OFDM符号，在试验过程中多次传输以获取不同时刻和不同传输距离的接收数据.图13（b）和（c）显示了某一时刻发送信号在传输距离分别为500 m 和1 000 m 处的接收数据信息.图14（a）和图14（b）分别给出了在不同传输距离下观测时间约为60 s 的河试信道脉冲响应的时变过程，可以看出，河试信道存在明显的多径效应和多普勒效应，根据船只0.5 m∕s 的漂移速度、信号中心频率25 kHz 及声速1 500 m∕s，可得出多普勒频移约为8 Hz.此外，由图14 可以看出，500 m 的河试信道环境更为复杂，由于传输距离的增加，有一部分反射径和折射径的能量损耗殆尽而无法到达接收端.因此，1 000 m 的河试信道脉冲响应图的路径数变少，多径时延也变小.

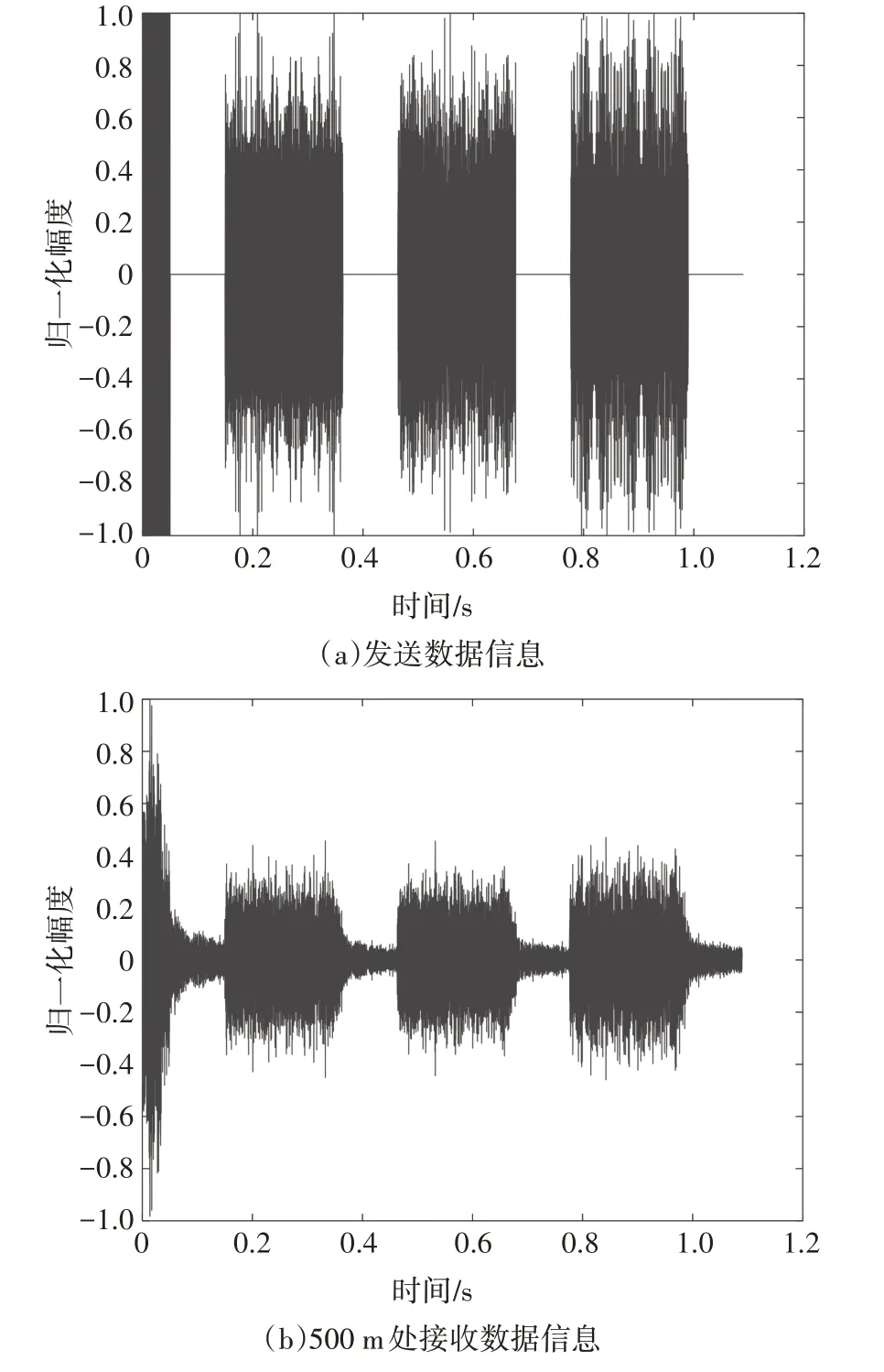
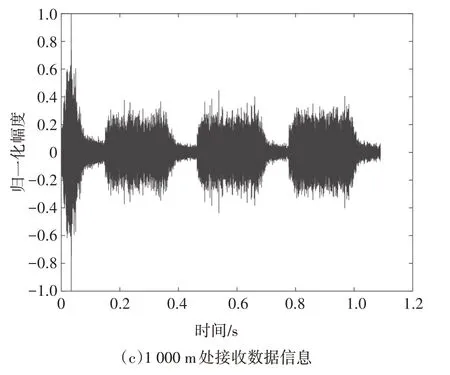
图13 发送和接收数据信息Fig.13 Send and receive data information

图14 河试信道脉冲响应Fig.14 River channel impulse response

在不同算法下，实际水声通信系统中的BER 曲线如图15 所示.其中DNN 模型和本文提出的PTRCNN 模型均在仿真环境2 下进行训练，然后直接加载训练好的网络参数进行测试.由于浅水环境中包含更多的噪声、更大的多径和多普勒频移，传统的PTR 算法随着信噪比的增加，误码率曲线趋于饱和，此时仅仅使用简单的PTR 算法无法很好地处理OFDM 系统中的ISI∕ICI，故增加信噪比也无法收获大的增益.而DNN 由于模型特点在河试信道环境中缺乏适应性，在图15 中表现的误码率性能几乎与传统算法相同，这表示DNN 无法通过训练好的网络参数直接用于实际水声通信系统中.与上述两种算法相比，本文提出的PTR-CNN 在实际水声通信系统能够实现可靠传输，对河试信道环境的敏感性更低，误码率性能得到提升.这意味着PTR-CNN 模型可以直接用于实际水声通信系统，并且可以用于快速时变的水声信道环境，无需额外训练开销.

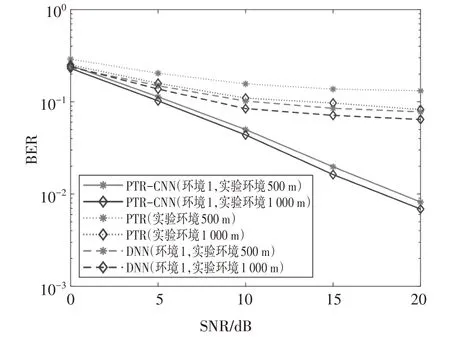
图15 不同算法在实际水声通信系统中的BER曲线Fig.15 BER curves of different algorithms in actual under water acoustic communication system

5 结论

本文针对水声通信中严重的多径效应和多普勒效应问题，构造了一种新型的基于PTR-CNN 的OFDM 水声通信系统.该方法一方面利用PTR 削弱信道的多径分量，又利用CNN 提取信号特征和信道特征进行训练，以对抗多径效应和多普勒效应带来的干扰，提升系统的信号检测性能.仿真和海河试验结果表明，与传统的接收端信道估计和信号检测算法相比，PTR-CNN 模型在较强的多径效应和多普勒效应下仍保持较强的信号恢复能力，具有一定的抵抗系统ISI 和ICI 的作用.与现有的DNN 系统相比，PTR-CNN 模型在水声信道环境失配时仍具有较好的误码率，对各种水声信道环境均具有鲁棒性.