一种基于深度强化学习的电网潮流分析方法

王 申，李文臣，贾培浩，黄彦浩，章姝俊

（1.北京九章云极科技有限公司，北京 100085；2.中国电力科学研究院有限公司，北京 100192；3.国网浙江省电力有限公司，浙江杭州 310007）

潮流计算作为电力系统的一种重要分析方法，快速、准确地估计电网潮流值是对电力系统稳定性与可靠性分析的前提，也是保证整个能源互联网稳定运行的必要条件[1]。随着社会的发展，电力需求不断提高，电网规模也在不断扩大，用于电网结构分析的潮流计算也变得越来越复杂[2-3]。传统的潮流分析已无法适应于现代电网架构，尤其是在能源互联网背景下，电网拓扑结构更为繁杂，这对潮流分析提出了新的挑战与更高的要求[4]。

在传统潮流分析中，人工经验的依赖程度高，且我国电网节点数量庞大，这导致时常出现计算不收敛的问题[5]。同时，近年来人工智能技术凭借优异的性能快速兴起并广泛应用于电网分析领域[6]。为此，提出了一种基于深度强化学习的电网潮流分析方法。其在传统潮流计算的基础上，利用深度双Q网络(Deep Double Q-Network，DDQN)自动调节收敛，并通过计算得到的潮流值完成电网分析，以便于进行电网调度。

1 电网潮流计算

一个典型的电力系统通常由发电机、变压器、负载和输电线路组成，且还可能包含其他元件，如分流器、柔性交流输电系统等[7-8]。在进行潮流计算时，通常将变压器、输电线路、电感、电容等器件看成线性网络的一个部分，等效成R、L、C构成的电路[9]。

1.1 潮流计算模型

若电网中存在n个节点，且网络结构已知，则节点电压与电流之间的数学关系表达如下[10]：

式中，Ii为节点i的注入电流，Uk为节点k的电压，Yik为节点i和k之间的导纳。

在实际运行的电力系统中，电流通常是三相的，且相较于节点的注入电流，注入功率更易被获取。因此，节点注入电流与功率之间的关系表示如下[11]：

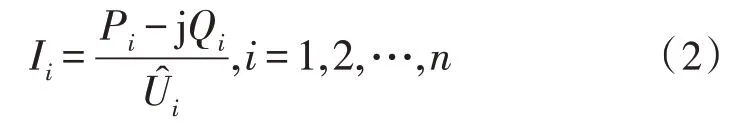
式中，Pi、Qi分别是节点i向电网中注入的有功功率与无功功率，为节点i电压Ui的共轭，j 为复数符号。

结合式（1）和式（2），能够获得用节点注入功率表示的潮流计算方程：

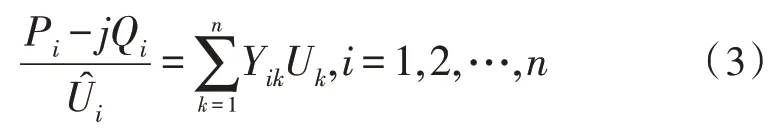
1.2 潮流计算流程

电网潮流计算的典型流程，如图1 所示。

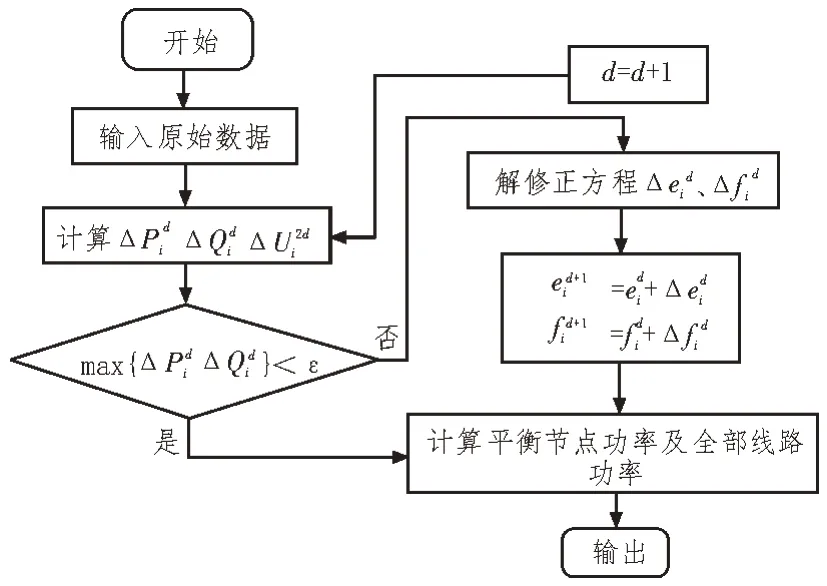
图1 潮流计算流程

首先，通过牛顿-拉夫逊法计算原始输入数据的有功功率变化值、无功功率变化值、节点电压，用于衡量计算的准确性。将Yik=Gik+jBik、U=ei+jfi代入式（3），通过数学运算得到：

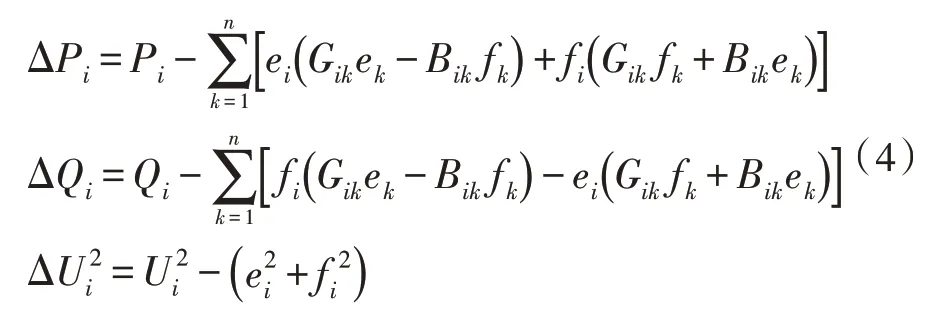
2 基于深度强化学习的潮流分析

2.1 深度强化学习

深度强化学习融合了强化学习与深度学习技术，其采用DDQN 进行潮流分析。其中，DDQN 结合深度学习与双Q 网络，克服了过拟合的问题[12-15]。DDQN 的网络结构如图2 所示，由感知网络与控制网络组成。

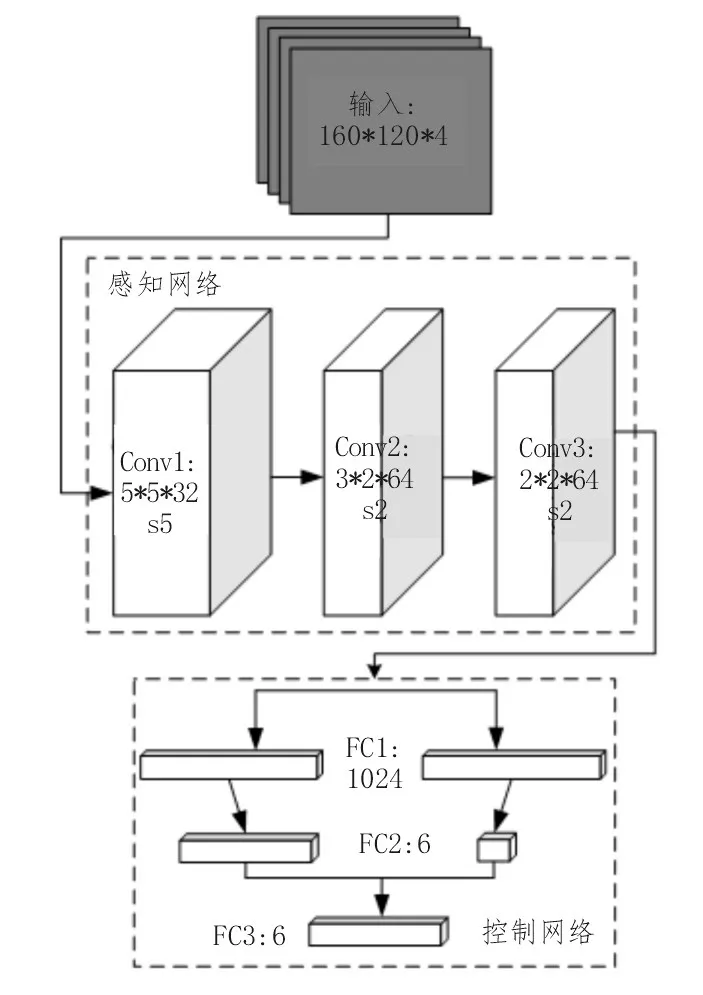
图2 DDQN的网络结构

其中，感知网络层是一个三层卷积神经网络(Convolutional Neural Network，CNN)，第一层CNN 使用32 个大小为5×5 的卷积核；第二层使用64 个大小为3×3的卷积核；第三层使用64个大小为2×2的卷积核，这3 层卷积神经网络的步长均设置为2。控制网络为决策网络，其具有两个完全连接(Full Connection，FC)层序列，分别用于估计每个动作的状态值与优势，其所有层的激活函数均使用ReLu 函数。

作为标准的强化学习方法，状态序列s被视为一个马尔可夫决策过程，并通过与环境互动做出决策[16]。在每一个时间，首先根据t时刻的当前状态值st选择一个动作at，然后由奖励函数产生奖励信号r(st,at)，最终通过动作得到下一个状态值st+1。累计奖励期望值为：

式中，λ为折扣因子，用来衡量当前与未来奖励的重要性。

深度强化学习算法的目标是使动作值函数Q最大化，则DDQN 的Q函数为：

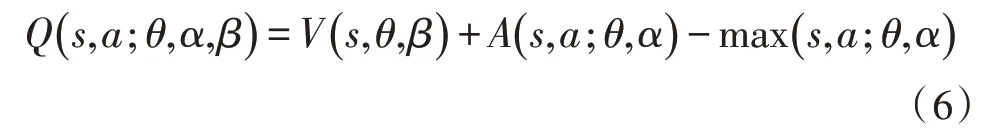
式中，θ为目标Q网络的参数，α和β为Q网络完全连接层的参数。则Q网络训练的损失函数为：

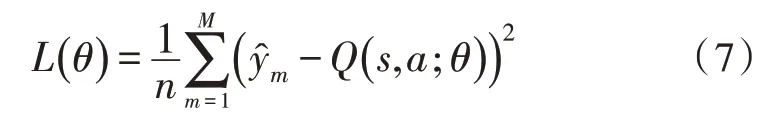
2.2 基于DDQN的电网潮流自动收敛调整

潮流计算收敛的调整第一步是改变潮流参数，第二步是按照变化后的潮流状态进行反馈，从而明确之后的操作。

1）状态空间

状态就是可观测变量，包含多个样本的潮流状态的状态空间表示为：

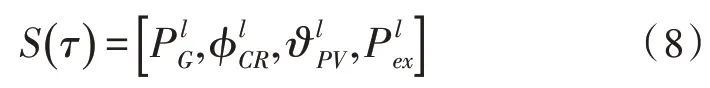
2）动作空间

动作就是可调节变量，主要包括发电机的功率改变量ΔPG、特定电容或电抗器以及增加PV 节点等。其数学表达式为：

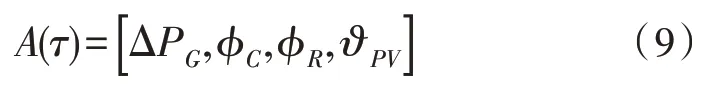
3）奖励函数

潮流计算的结果分为收敛与不收敛两种。当收敛时，奖励值设成较大的正数；反之，设成较小的负数。数学表达式为：

综上所述，基于DDQN 的潮流收敛调整流程如图3 所示。

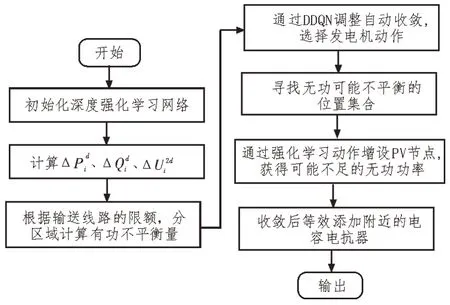
图3 潮流收敛调整流程

3 实验结果与分析

3.1 训练过程

为了论证DDQN 的学习性能，将其与传统深度强化学习网络进行对比分析。所得到的奖励值对比曲线如图4 所示。

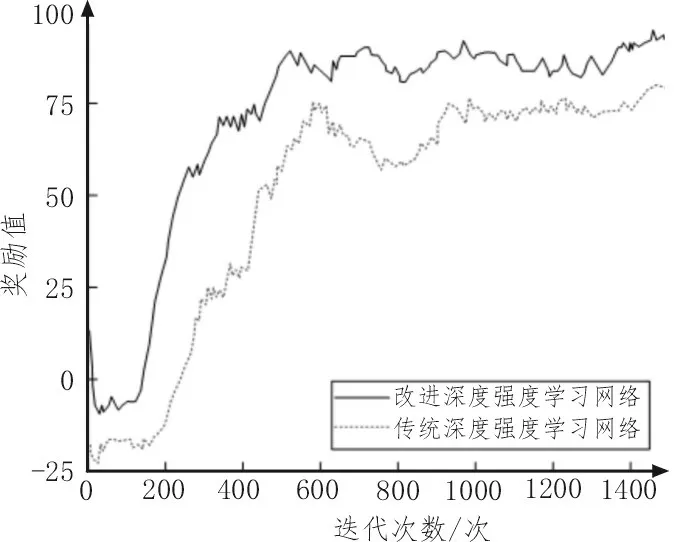
图4 改进前后网络的奖励值对比曲线

从图4 中可以看出，改进深度强化学习网络所得到的奖励值明显高于传统方法，说明改进网络对训练效率具有较好的提升效果。当迭代次数为500时，其奖励值趋于稳定，后期仅在小范围波动，最终趋于100。而传统深度强化学习网络的收敛速度慢，且奖励值较低，说明会存在计算不收敛的情况。故DDQN 的训练效果优于传统方法，能够更优地应用于电网潮流计算分析。

3.2 潮流自动收敛性能分析

为了论证所提方法的自动收敛能力，设置了两种实验方案进行论证。方案1：包含3 台G2、G8 等级的发电机，12 台电容器和15 台电抗器；方案2：包含3台G3、G8 等级的发电机，10 台电容器和11 台电抗器。对构建的电网进行潮流分析，其收敛结果如表1所示。

表1 某地区电网潮流收敛结果

从表1 中可以看出，该地区电网方案2 的收敛结果高于方案1。由于电网调度时，需要投入和切除的电容器数量越多，则可操作的范畴就越广，相应的无功功率就难以达到平衡状态。方案2 中，当每个计算周期为100 步时，45%能够快速收敛，10%难以在计算步长内完成收敛。当每个计算周期为200 步时，仅有3%不收敛。如此便可看出，调整收敛的效果更优，在实际工程中具有一定的可行性[17-18]。

3.3 潮流调整能力分析

某地区实际电力系统在常规运行方式下的潮流分布，如图5 所示。

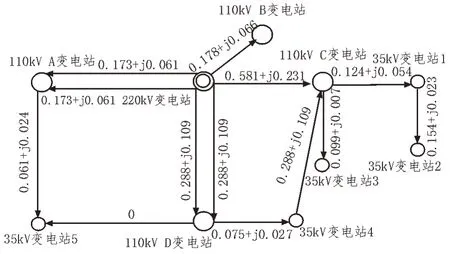
图5 常规运行方式下的潮流分布

从图5 中可以看出，整体上电网能够维持平稳运行，但局部存在潮流分布不均衡的问题。如：1）B变电站主变负载严重偏低，约为10%；2）35 kV 变电站1 负载率达到103%，存在严重过载；3）C 变电站由于有新能源接入，因此扰动较大，存在运行不稳定的现象。

利用所提方法对该地区的潮流进行计算分析，并采取负荷转移、双电源供电等措施调整潮流分布。综合优化后的潮流分布，如图6 所示。

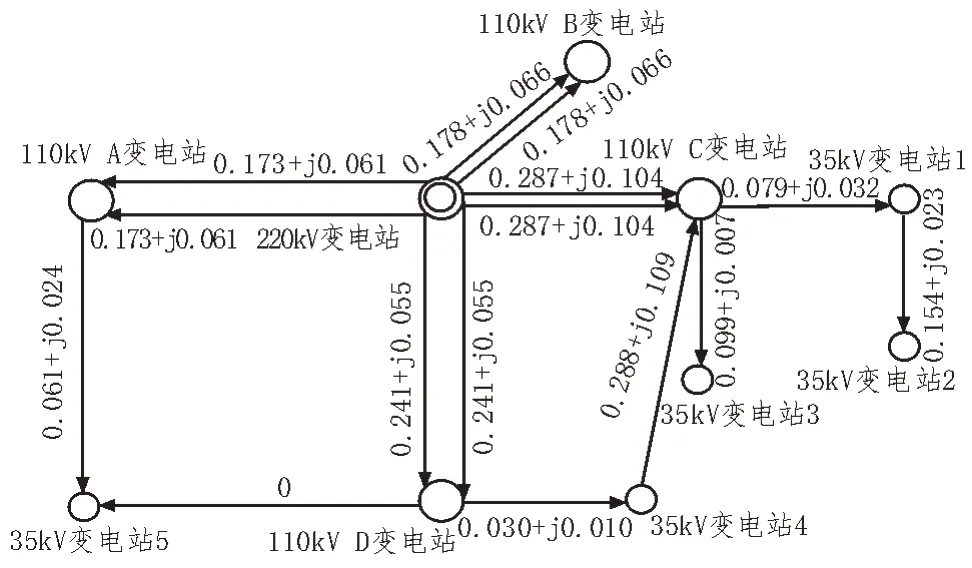
图6 综合优化后潮流分布

从图6 中可以看出，通过DDQN 自动调节收敛得到的潮流值更为合理，其潮流分布有利于维持220 kV主网的稳定运行。同时合理利用轻载站点的变压器，缓解了各个重载站点。在110 kV 变电站中，提高了B 变电站的负载率，由12%上升至19%，使变压器的利用更为合理。C 变电站的负荷并未改变，但采用双回路供电提高了系统的稳定性。在35 kV 变电站中，通过转移负荷、修建隘口站等措施优化潮流分布，从而解决了重载或过载的问题。

4 结束语

新能源技术的快速发展推动了电网架构的更新换代，同时人工智能技术的兴起为潮流计算提供了一种新的优化思路。为此，提出了一种基于深度强化学习的电网潮流分析方法。在传统电网潮流计算的基础上，利用DDQN 动态调节电力网络参数，并根据收敛后得到的潮流值调整电网运行状态。基于PSASP 平台利用所提方法对某地区电网数据进行潮流分析的结果表明，DDQN 在迭代500 次后奖励值趋于100，且投切电容器数量较少的系统，有97%的潮流计算能够收敛。同时，经过分析控制后的电网潮流分布，有效缓解了变压器重载或轻载以及部分变电站由双回路供电的情况，提高了电网运行的稳定性。

由于所提方法采用的DDQN 网络在参数调节过程中耗费的时间较长，因此在接下来的研究中将重点考虑并行计算，以提高潮流分析的效率。