基于DEM-CFD耦合仿真的盘棒复合转子研磨特性

孙飞，吴波，何康，杨权，张秀香，孟超

(1.宿州学院 机械与电子工程学院，安徽 宿州，234000；2.宿州学院 高端微纳研磨装备校企协同创新工程中心，安徽 宿州，234000；3.安徽儒特实业有限公司，安徽 宿州，234000)

超细粉体是指从微米级到纳米级的粉体材料。超细粉体具有2种特殊效应，即颗粒体积变小引起的体积效应和颗粒表面原子数目的比例增加引起的表面效应。两种特殊效应使超细粉体与普通材料相比，其物理性能与化学性能有明显的区别，甚至会表现出新的物理化学性能。如李晶等[1]采用湿法研磨吡虫啉纳米农药，改善农药性能，提高农药利用率；王小康等[2]采用湿法研磨技术制备铝碳酸镁纳米晶体，提高了药物颗粒悬浮液抗酸效果，起效速度加快。因此，湿法研磨技术是获得超细粉体和提高产品性能的主要技术手段之一。

研究湿法研磨机的研磨特性影响因素对于提高研磨效率至关重要。目前湿法研磨特性研究方法主要分为研磨过程模拟仿真和研磨试验2种。其中，研磨试验方法确定研磨工艺参数较为准确，但是存在初期优化目标不明确，研究周期长等缺点。而模拟仿真能够快速地确定不同工艺参数对研磨效率的影响，为试验提供优化方向。如马畅[3]采用EDEM软件中对卧式砂磨机的研磨过程颗粒运动规律进行仿真模拟，研究影响研磨效率和能量的主要因素。孙小旭等[4]利用CFD仿真方法对超细磨用搅拌装置进行仿真模拟，研究不同参数对流场的影响。这些研究为湿法研磨特性的分析提供较好的借鉴，但较多的模拟仿真存在研究对象单一，颗粒相与流体相分析相互独立，仿真过程与实际研磨过程不吻合等缺点。

DEM-CFD耦合方法克服了上述缺陷，该方法综合考虑流场作用力和颗粒作用力，能够准确分析颗粒相与流体相之间的相互作用，研究结果更准确。因此，为了研究CJ02卧式盘棒复合转子湿法研磨机的研磨特性影响因素，采用DEM-CFD耦合方法对农药混悬液研磨过程进行仿真模拟，研究转速、碰撞能量和碰撞频率等参数对研磨效果的影响。

1 研磨材料和模型属性

1.1 材料属性

湿法研磨的材料是一种农药悬浮液，材料属性见表1。农药的密度、黏度、泊松比、剪切模量、研磨介质密度等来源于制造商提供的参数。把研磨介质剪切模量降低104，此方法适用于颗粒碰撞软件仿真，目的是提高软件模拟仿真的速度，减少仿真时间[5]。

表1 材料属性

1.2 卧式湿法研磨机模型设置及研磨介质属性

研究采用安徽儒特实业有限公司提供的0.2 L卧式湿法研磨机，研磨转子型式为盘式+棒销式转子，结构和尺寸见图1。研磨腔内颗粒数量是决定仿真模拟计算成本的关键因素。为了进行有效且快速的仿真模拟，研磨机所有部件等比例缩小，缩小后其有效研磨容积为0.05 L。研磨机填充率为70%，研磨介质颗粒直径为1.2 mm，材料为氧化锆，空隙率为0.4，研磨机腔内颗粒数量约为25 000 个。

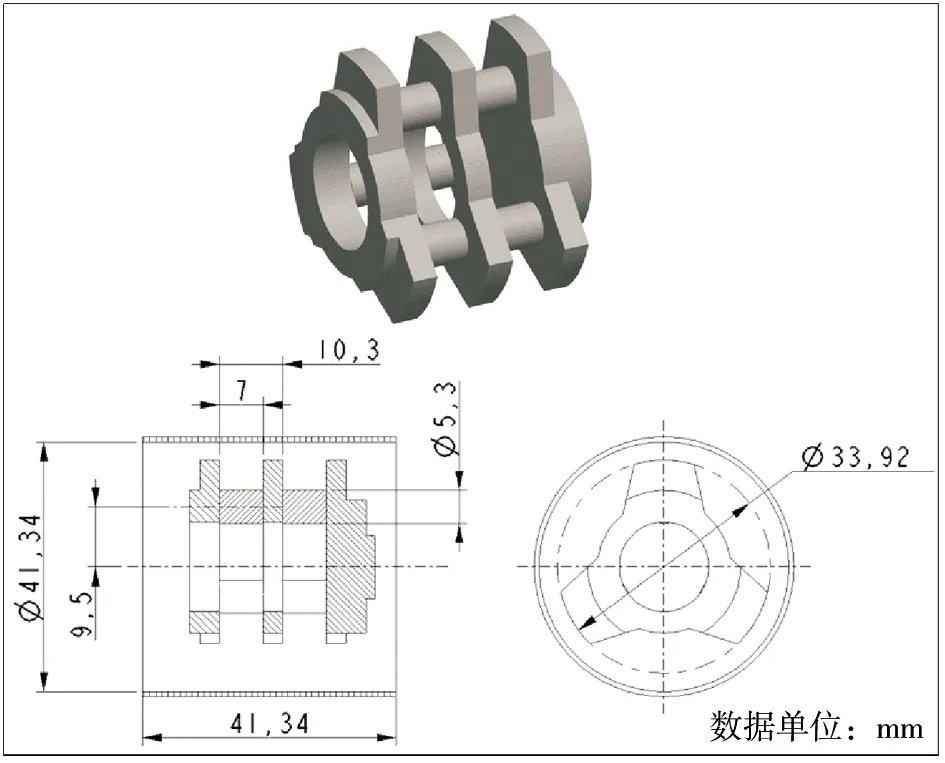
图1 0.2 L卧式湿法研磨机转子结构示意图

2 模拟仿真设置和方法

2.1 离散元法和计算流体动力学模拟

由颗粒物质与流体(气体、液体)组成的混合系统一般称为颗粒多相流系统。研究初期多采用欧拉-欧拉方法[6]，通过每种流体的浓度变化及分布特性来表示系统。但是该方法本身具有局限性，不能够表征颗粒级别上的属性，如颗粒形状、碰撞规律、粒径分布和运动轨迹等。而颗粒的属性对于湿法研磨的颗粒运动起到重要的作用。

离散元方法(DEM-CFD)中DEM方法能够准确分析颗粒形状和运动规律，结合了流体力学(CFD)方法，能够准确分析颗粒相与流体相间的相互作用。耦合计算原理见图2，EDEM-Fluent耦合过程是一个瞬态双向数据传递的过程。首先，利用Fluent计算1个时间步长的流场信息。其次，启动EDEM进行相同时间迭代，利用耦合接口将颗粒的位置、运动、体积、温度等信息传递至Fluent中，计算颗粒与流体的相互作用。最后，流体对颗粒的作用通过接口程序传递至EDEM影响颗粒的运动，颗粒对流体的作用则通过动量源相的方式反馈至流体，影响流体的运动。如此，经过逐步迭代，实现全过程的瞬态模拟。

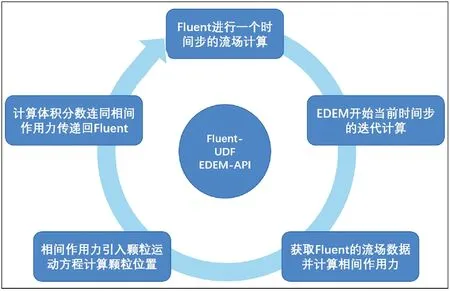
图2 DEM-CFD耦合仿真计算原理

2.2 网格划分

DEM-CFD耦合仿真使用软件为EDEM 2018和Fluent 19.1。研磨机的运行过程中，研磨筒体内由流体介质、研磨介质和物料(浆料)组成，当三者充分混合后属于多相流范畴。湿法研磨机配备冷却系统，研磨过程中保持恒温恒压，研磨介质颗粒粒径小，农药悬浮液黏度高，研磨转速高，基于以上考虑，对研磨机筒体内部搅拌运动和内筒壁结构进行简化处理。

1)将内筒体视作体积相同的简单圆柱体，忽略流体温度的影响。

2)在紧贴转子处设置包浆区，将其视作转子的影响区域，以包浆区转动代替转子转动。

3)将物料与流体介质的混合溶液以浆料代替，将其视为一种均一的单相牛顿流体。

对模型进行去圆角和去倒角处理，有利于网格的划分，减少网格的数量。一般使用三角形/四面体网格来节省划分网格的工作量[7]。本次网格划分中网格质量最小值为0.12，最大值为1.00，平均值为0.83，单元质量标准差为0.01，网格数量63 086 个。

2.3 边界条件设置

DEM和CFD模拟耦合采用DPM离散相模型。采用的模型是EDEM中的Hertz-Mindlin接触模型和CFD中的标准k-ε湍流模型[8]。根据网格属性采用三维稳态格林-高斯节点基求解器，计算更精确，更少伪扩散[9]；Fluent中旋转搅拌流场选择多参考坐标系模型(MRF)进行处理[10]，对于DEM-CFD耦合颗粒流体间作用力，本次仿真模拟采用了Koch-Hill曳力定律[11]。

DEM-CFD耦合是按照Fluent时间步执行。在仿真设置中，采用固定时间步长方法，时间步长为0.01 s，总时间步长数为450步。收敛准则为所有方程残差设置为10-3。连续性方程残差下降到10-4，其他分量残差下降到10-5，模拟仿真满足收敛标准。

研究基于相同研磨介质及填充率的状态下，不同转子转速对研磨效率的影响。根据实验参数对转子转速进行设定，转速分别是1 500、2 000、2 500、3 000和3 500 r/min。

3 仿真结果及分析

湿法研磨机的研磨效果主要来自物料与研磨介质颗粒之间的碰撞接触，影响研磨效率的直接因素是研磨介质颗粒与物料之间的接触力、碰撞频率和碰撞强度。因此，仿真模拟研究将物料与研磨介质颗粒的碰撞转化为研磨介质颗粒之间的碰撞。

3.1 速度场分析

3.1.1 速度积分值

为了对比转速对研磨效果的影响，选取速度面积积分值作为表征研磨作用强度的参数[12]。在距离筒体壁面1 mm处，建立二次圆柱曲面，曲面不同转速下速度积分值见图3。由图3可知，速度积分随转速提高而逐渐增大，呈线性增大趋势。这是由于流体受到离心力的作用，流体与研磨筒体壁面发生碰撞，随着转速升高，壁面处流体速度逐渐增大，碰撞强度不断增大。因此，在实际研磨过程中，提高转速可以获得更大粉碎作用力，有利于提高研磨的效果。

图3 速度面积积分随转速变化规律图

研磨机转子外径与筒体壁面之间的区域由于离心力的作用，研磨介质颗粒大量聚集。为了研究该区域的研磨效果，选取转子外径与筒体壁面之间的区域(转子半径为16.96 mm，筒体半径为20.67 mm，下同)，每隔1 mm建立1个圆柱曲面，求解出各曲面在不同转速下的平均速度，见图4。由图4可知，随着转速增大，速度平均值呈现线性增大的趋势，即提高转子转速，会提高流体速度，从而提高研磨介质颗粒总动能，提高研磨的效率。

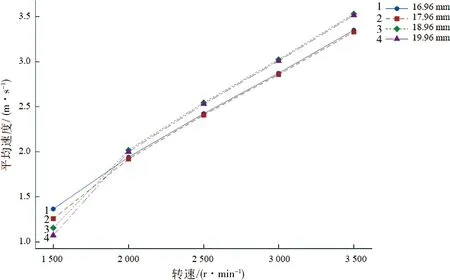
图4 不同转速下各曲面平均速度图

3.1.2 速度梯度

研磨介质动能直接来自于流体，流体速度梯度较大的地方，研磨介质颗粒的碰撞更加剧烈，因此，分析流体的速度梯度可以预测研磨机的研磨效果。不同转速下速度梯度等值线分布类似，这里选取2 500 r/min速度等值线进行分析，见图5。由图5可知，靠近筒壁和转子盘销附近等值线密集区域，速度梯度较大。而研磨筒体两端和内部区域速度等值线稀疏，速度梯度较小，因此，其研磨效果相对较差。

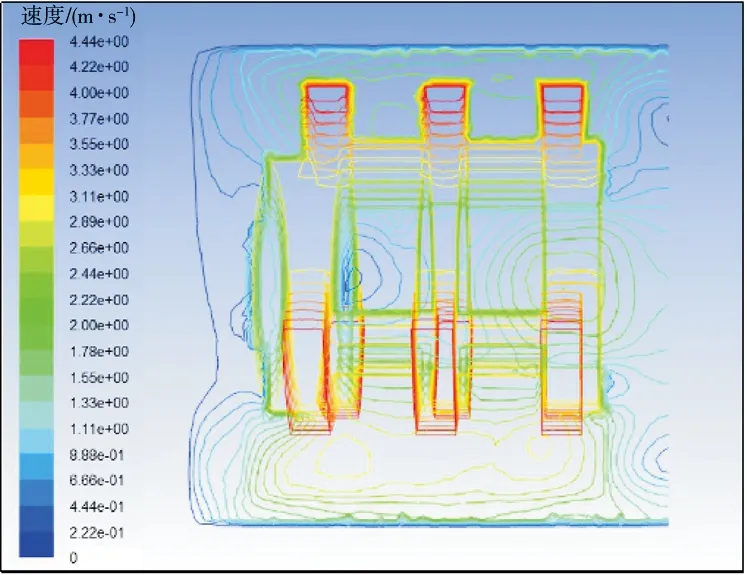
图5 速度等值线图(2 500 r/min)

为了进一步对比转速变化时流场能量差，根据转子模型的结构尺寸，选取转子外径与筒体壁面之间的区域，每间隔0.2 mm建立1个圆柱曲面，根据不同转速下的各曲面速度梯度作出图6所示的点线图。由图6可知，所有曲面的速度梯度均随着转速提高而增大。在靠近筒壁处(19.36～19.96 mm)和转子附近(16.96～17.56 mm)，速度梯度较大，说明此处流体的剪切力作用较强。在流场速度交界处其能量差较大，研磨效果较好，此处研磨效率较高，为研磨的主要发生区域。

图6 不同转速下各位置速度梯度

3.2 颗粒场分析

由速度场分析可知，各区域的速度梯度不同，速度交界处能量差大，为验证各区域研磨介质的碰撞与速度场的符合性，将研磨筒体内部划分成3个区域：SE-1区(转子外径与研磨筒壁间区域)、SE-2区(转子直径包裹区域)和SE-3区(转子两端区域)，具体见图7。

图7 研磨筒体区域划分示意图

根据EDEM模拟仿真中研磨介质在2 500 r/min下不同区域的碰撞次数(表2)可以得知，SE-1区域，即速度等值线密集区域，发生碰撞的次数最多，1 mm3碰撞次数约为10次；SE-2区域，即速度等值线稀疏区域，研磨介质碰撞次数最少，1 mm3碰撞次数约为3次，颗粒碰撞频率与速度场分析完全吻合。

表2 各区域碰撞次数

3.3 碰撞能量分析

研磨初始，研磨介质颗粒的总能量来源于流体和转子的动能，研磨介质颗粒碰撞后，研磨介质的总能量等于碰撞能量与研磨介质动能之和(研磨腔容积较小，忽略重力势能)。因此，可以根据研磨介质颗粒之间的碰撞能量预测研磨介质颗粒与物料间的碰撞，进而分析不同转速下的研磨效率。

3.3.1 碰撞总能量对比

通过EDEM导出各转速下颗粒碰撞总能量数据，具体见图8。由图8可知，随着研磨机转速提高，研磨介质颗粒碰撞总能量逐步提升，因此，提高转速有利于提升研磨的效率。但是随着转速提高，研磨介质碰撞总能量增长缓慢，转速由1 500 r/min提高至2 000 r/min，碰撞总能量增大约250%；转速由2 000 r/min提高至2 500 r/min，碰撞总能量增大约30%。转子转速与研磨介质碰撞总能量之间并非呈线性增长关系，因此，当转速超过一定限值，继续提高转速，研磨效率提升有限。

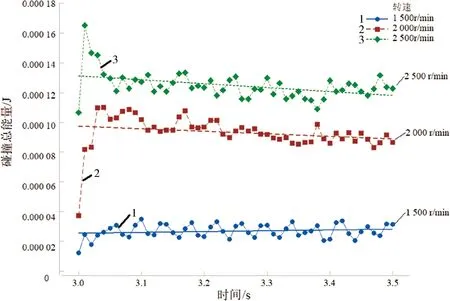
图8 不同转速下碰撞总能量对比

3.3.2 碰撞切向能量和法向能量对比

研磨介质颗粒碰撞在湿法研磨过程中起主要作用，研磨介质颗粒的碰撞分为法向碰撞和切向碰撞。为了研究研磨介质颗粒碰撞的方向和主要作用力，通过EDEM导出各转速下研磨介质颗粒切向碰撞能量和法向碰撞能量数据，取总模拟时间的平均值进行对比，见图9。由图9可知，研磨介质颗粒平均切向碰撞能量远大于平均法向碰撞能量，所以，研磨介质颗粒的碰撞过程中，切向碰撞是主要的碰撞形式，剪切力在研磨过程中起主要作用。

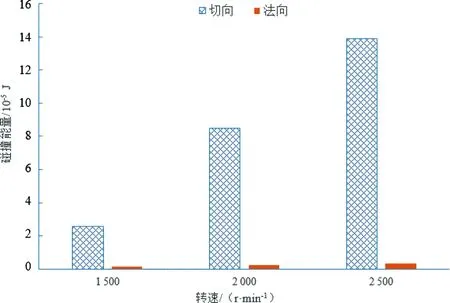
图9 不同转速下平均切向和法向碰撞能量对比

3.3.3 研磨机能量分析

通过研究得出，高速状态下研磨机在高速湍流状态下其功率近似为[13]

P=2.15d5N3ρsus

(1)

式中：P为研磨机功率，W；d为搅拌器直径，m；N为转子转速，r/s；ρsus为悬浮液的浓度，kg/m3。悬浮液浓度、搅拌器直径均属于定值，变量为转速，转子转速在1 500、2 000和2 500 r/min时电机功率的提升与碰撞能量提升的对比如下：

(2)

(3)

(4)

(5)

根据研磨机不同转速的电机总能量比值与颗粒碰撞能量比值的结果，可以得知，当研磨机转子转速从1 500 r/min提高至2 000 r/min，电机的功率提高235.85%，研磨介质颗粒碰撞能量提高364.8%，研磨工作效率提升。当转子转速从2 000 r/min提高至2 500 r/min，电机功率提高172.8%，研磨介质颗粒碰撞能量提高133.9%，研磨工作效率降低。研磨机能量分析进一步验证当转速大于2 000 r/min，继续提高转子转速，研磨机工作效率下降，研磨经济性差。

4 结论

1)研磨机筒体内靠近筒壁处和盘式转子附近速度梯度最大，剪切作用力强，研磨效果较好；研磨筒体两端和内部区域速度梯度小，研磨效果相对较差。

2)提高转速，研磨介质碰撞总能量增大，有利于提升研磨效率，但是转速大于2 000 r/min，继续提高转速，研磨工作效率下降，研磨经济性差。

3)研磨介质颗粒的切向碰撞能量远大于法向碰撞能量，研磨过程中起主要作用的是研磨介质颗粒相互接触时切向力。