四足仿生机器狗运动控制研究

周永强，李 佳，崔 晔，孙 强

(国网保定供电公司，河北 保定 071051)

0 引言

四足仿生机器狗是一种模拟四足生物狗运动的足式机器人，相较于单足或双足仿生机器人具有平稳性强、灵活性高的特点，而对比六足或八足等多足仿生机器人又具有更大的腿部移动空间。此外，由于在平坦路面具有高速动态性和在复杂地形环境中自适应能力较强，四足仿生机器狗已成为各国机器人研究的重点。然而，由于技术限制等原因，四足仿生机器狗的运动控制还存在平衡控制能力较差、轨迹跟踪能力有待提高的问题。为解决上述问题，Huang Yezhong等针对仿生机器人控制的不确定性和干扰问题，提出基于模型预测控制(model predictive control，MPC)的控制方法，并通过iLQG算法进行优化。其研究结果表明，以上方法表现出良好的收敛性和跟踪效果[1]。Ming Wang等提出一种迭代学习的仿生鱼控制方法，从而为软体动物的控制提供借鉴与参考[2]。司海飞等[3]基于虚拟模型，研究了四足仿生机器人对角小跑步态非线性控制方法，通过求导四足仿生机器人平面坐标系姿态误差微分方程结果，设计了四足仿生机器人驱动控制器，实现了对四足机器人的对角小跑步态非线性控制。张亮等[4]、张伟等[5]通过构建四足仿生机器人运动学模型及深度强化学习方法，加强了系统对四足仿生机器人的运动控制，具有一定的实用性。

基于上述研究基础，本文设计了一种基于模型预测控制的四足仿生机器狗运动控制器。该设计通过构建四足仿生机器狗离散线性化误差状态空间、目标函数，以及四足仿生机器狗的运动条件，实现了对四足仿生机器狗的运动控制。

1 四足仿生机器狗运动学模型构建

四足仿生机器狗运动简图如图1所示。

图1 四足仿生机器狗运动简图

根据运动学关系，可以得到：

(1)

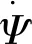
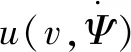
(2)

式中：r为规划路径的参考值。

对式(2)进行近似线性化处理，将每个状态点进行泰勒展开[6]，同时忽略高阶项，可得到：

(3)

将式(2)、式(3)相减，得到的经过线性化后的四足仿生机器狗误差模型为：

(4)

为了使预测模型能用于轨迹控制器，对式(4)进行离散化处理，得到：

(5)

2 四足仿生机器狗控制器设计

2.1 控制器设计思路

模型预测控制是一种特殊的控制方法，常用于避障任务领域，可处理优化目标和约束优化控制，具有稳定性强、可靠性高的特点。模糊预测控制的思想是将控制序列的第一个最优解滚动向前，得到预测系统的未来输出值，包括预测模型、滚动优化、反馈矫正三部分[7-9]。预测模型是控制的基础，具有展示系统过程历史信息和未来状态行为的功能，主要包括传递函数、状态方程式、非参数模型等预测函数[10]。滚动优化主要为反复滚动优化，相较于传统最优控制，具有良好的自适应性和鲁棒性。反馈矫正的主要作用为确保模型预测控制精度，以及减小模型预测误差。基于模型预测控制的仿生机器狗轨迹控制如图2所示。

图2 基于模型预测控制的仿生机器狗轨迹控制框图

由于模型中加入了反馈矫正，提高了模型预测的抗扰动性和不确定性。基于模糊预测控制的特点，将该模型应用到四足仿生机器狗参考轨迹的跟踪。由图2可知，模型预测控制模块首先利用当前反馈的状态量，通过离散化线性误差预测未来状态；然后根据设定的目标函数和约束条件，实现空置量的最优输出；最后将最优控制量输入位姿控制系统，从而通过位姿控制实现轨迹的运动控制。

2.2 目标函数设计

结合上述运动学模型，以及考虑到运动控制的目的，将模型预测控制器的目标函数设定为：

uT(k+j-1)Ru(k+j-1)

(6)

由式(6)可知，该目标函数可转化为标准的二次规划问题，但存在控制量突变，进而导致控制系统跳变[11]。为解决该问题，采用式(7)所示的软约束法对目标函数的条件进行约束。

(7)

式中:Np为越策时域；Nc为控制时域；ρ为权重系数；ε为松弛因子。

将式(4)进行转换，得到式(8)：

(8)

根据式(8)的转换，推导出系统的预测输出为：

Y(t)=Ψtξ(t|t)+ΘtΔU(t)

(9)

将式(9)代入式(7)，得到基于离散误差状态空间中的目标函数。

2.3 约束条件

考虑到四足仿生机器狗运动过程中的稳定性，对其控制量和控制增量进行限制。具体约束条件为[12]：

umin(t+k)≤u(t+k)≤umax(t+k),k=0，1，...，Nc-1

(10)

Δumin(t+k)≤Δu(t+k)≤Δumax(t+k),k=0，1，...，Nc-1

(11)

基于以上约束，将式(11)转换为：

Umin≤AΔUt+Ut≤Umax

(12)

式中：Umin为控制时域内控制量的下限集合；Umax为控制时域内控制量的上限集合。

(13)

式中：Im为四足仿生机器狗三维维度的单位矩阵；⊗为克罗内克积。

将目标函数转化为标准二次型形式，同时结合约束条件，从而将目标函数转换为以下问题的求解[13]：

J[ξ(t)，u(t-1)，ΔU(t)]=[ΔU(t)T，ε]THt[ΔU(t)，ε]+Gt[ΔU(t)T，ε]
s.t.ΔUmin≤ΔUt≤ΔUmax,Umin≤AΔUt+Ut≤Umax

(14)

在每个控制周期，对式(14)进行求解，从而得到：

(15)

3 仿真试验

3.1 避障轨迹设置

为验证基于模型预测控制的效果，设置一个r=0.1 m的圆柱障碍物，由四足仿生机器狗按照式(18)的轨迹方程行走。该运动轨迹包括三步。第一步为20°的弧线，如式(16)所示。第二步为-20°的弧线，如式(17)所示。第三步为直线匀速行走，如式(18)所示。

(16)

(17)

(18)

此外，为测试基于模型预测控制的四足仿生机器狗在不同速度和控制参数下轨迹的跟踪性能，本试验还设置了不同条件的工况。

3.2 仿真结果

3.2.1 不同控制参数下的跟踪结果

控制量ur=[-0.1 m/s 0.025 rad/s]。

控制量约束ukin：上界[-0.05 m/s 0.05 rad/s]；下界[-0.15 m/s-0.05 rad/s]。

控制增量约束Δukin：上界[0.00 lm/s 0.000 5 rad/s]；下界[-0.15 m/s-0.05 rad/s]。

工况1参数：误差权重系数Q=diag[100 100 100]；控制权重系数R=diag [20 000 20 000]。

工况2参数：误差权重系数Q=diag[l 1 1]；控制权重系数R=diag[50 000 50 000]。

工况3参数：误差权重系数Q=diag[1 1 1]；控制权重系数R=diag[20 000 20 000]。

设定避障轨迹如图3所示。

图3 设定避障轨迹示意图

在不同的控制参数下，四足仿生机器狗在不同工况下的轨迹和偏航角变化如图4所示。

图4 不同控制参数下轨迹和偏航角变化

由图4可知，不同工况条件下，四足仿生机器狗都能较好地跟踪参考轨迹，并将误差控制在5 cm内。但由于存在偏航角偏差，导致轨迹出现一定的下行。

综合表1和图4的结果可知，随着误差权重系数Q的增大，轨迹波动幅度逐渐增大，对轨迹误差的反应更加灵敏；随着控制权重系数R的增大，四足仿生机器狗的惯性也逐渐增大，但运动平稳。究其根源，是通过模糊预测控制算法提高了四足仿生机器狗整体运行的平稳度，同时也减缓了误差的反应。

四足仿生机器狗在不同控制参数下前进速度和偏航角速度变化如图5所示。

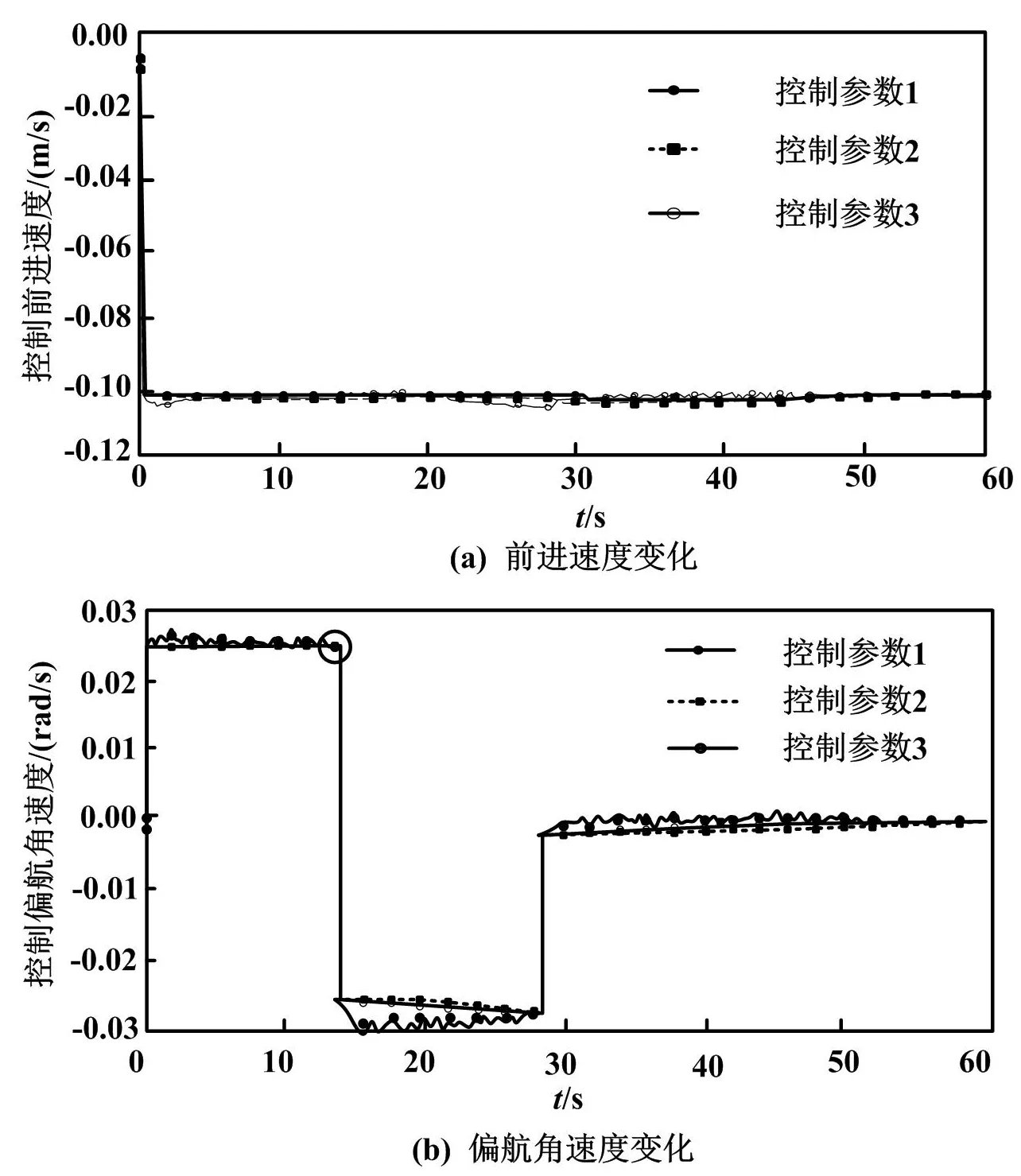
图5 不同控制参数下前进速度和偏航角速度变化

结合表1和图5可知，随着Q的增大，系统的波动幅度逐渐增大，但对轨迹误差的反应更加灵敏；随着R的增大，系统惯性逐渐增大，控制更加平稳，但对误差反应逐渐减缓。

3.2.2 不同参考速度下的跟踪结果

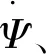
误差权重系数Q=diag[100 100 100]。

控制权重系数R=diag[20 000 20 000]。

控制量约束ukin：上界[-0.05m/s 0.05 rad/s]；下界[-0.15m/s -0.05rad/s]。

控制增量约束Δukin：上界[0.001 m/s 0.000 5 rad/s]； 下界[0.001m/s 0.000 5rad/s]。

工况1参考速度：[-0.05 m/s 0.012 5 rad/s]。

工况2参考速度：[-0.l m/s 0.025 rad/s]。

在不同参考速度下，四足仿生机器狗的轨迹变化如图6所示。

图6 不同参考速度下四足仿生机器狗状态量变化

由图6可知，在不同的参考速度下，机器狗可较好地跟踪参考轨迹，并将误差控制在预设范围内。另外，同样因偏航角问题，使得Z方向出现小幅度的偏离。

综上可知，低速状态下，四足仿生机器狗的转向相对于高速状态下更容易完成，且对控制量的控制更加精准，由此表现出对轨迹和偏航角更好的跟踪。

图7为四足仿生机器狗在不同参考速度下的前进速度变化和偏航角速度变化。

图7 不同参考速度下四足仿生机器狗控制量变化

由图7可知，四足仿生机器狗可良好地跟踪输入的参考前进速度和偏航角速度，且跟踪误差在预设的允许范围内。低速工况下，四足仿生机器狗控制量变化相较于高速工况的控制量变化更平稳。其原因是低速工况下的仿生机器狗转向更易实现。

4 结论

本文通过模型预测控制方法，研究了四足仿生机器狗的避障轨迹问题。通过研究得出：该方法在不同控制参数和参考速度下可有效跟踪给定的避障轨迹，且跟踪轨迹误差在10 cm以内，偏航角误差在2°以内，满足规定约束范围。同时，研究发现，不同参数设置对四足仿生机器狗运动控制效果不同，误差权重系数Q越小，其稳定性越强，但响应速度越慢；控制权重系数R越小，其稳定性越强，控制量的变化越平缓，但响应速度越慢；参考速度越小，其转向性能越好，偏航角的误差越小。