基于改进FxLMS算法的悬臂梁振动研究

张丽雯,姜金华

(1.上海第二工业大学资源与环境工程学院，上海 201209；2.上海第二工业大学智能制造与控制工程学院，上海 201209)

0 引言

振动[1]是物体的往复运动，是自然界和工程界的普遍现象。人与机械交互时，噪声问题也通常被归为振动问题[2]。工业生产制造中难免会产生振动，而这种振动会影响到工业生产。特别是对于精密器件和超精密加工设备的使用，任何微小的振动干扰都很有可能对测量数据和设备本身产生严重的影响。因此，如何有效地控制振动一直是国内外深入研究的课题。

主动噪声控制(active noise control,ANC)是一种振动控制的新技术[3]。与被动振动控制相比，主动振动控制对于低频的隔振效果更好，而且对外界环境有较强的适应能力。如今，主动振动控制被广泛应用于工业领域。自适应滤波算法是主动噪声控制研究的重点。对于复杂设备与装置可能存在的结构非线性与时变环节，自适应滤波算法具有较好的技术特点与优势[4]。常用的自适应滤波算法是基于维纳滤波的最小均方(least mean suqare,LMS)算法。该算法具有结构简单、性能稳定、计算复杂度低和易于实现等特点。

20世纪80年代，Morgan、Widrow及Burgess提出了获得广泛应用的滤波-x最小均方(filtered-x least mean suqare,FxLMS)算法[5]，解决次级通道引起的系统不稳定问题。2011年，周亚丽等提出了基于反正切变换的滤波-x最小均方算法(filtered-x arctangent least mean suqare,FxatanLMS)[6]，解决了脉冲噪声高尖峰特性引起的系统不稳定问题。2013年，Wu提出了Fair算法[7]，利用Fair函数对误差信号进行非线性变换。Fair函数的特性是连续平滑且仅有一个可调阈值参数，避免了选择参数和估测阈值的麻烦，算法性能更好。

Oh.J等利用FxLMS算法对悬臂梁主动振动控制系统进行了试验研究，验证了FxLMS算法的可行性[8]。Meng等提出了一种基于压电堆作动器的直升机机身多输入多输出多谐波前馈自适应自动电压控制(automatic roltagecontrol,AVC)方法。该方法由谐波系数辨识和多输入多输出多谐波(multi-input multi-output multi-harmonic,MIMOMH)前馈FxLMS算法组成[9]。Li等将反馈FxLMS算法和比例积分微分(proportional integral differential,PID)控制器相结合，提出了混合PID-FxLMS算法，并将其应用于压电悬臂梁振动控制中[10]。王欢等通过有限元模型，应用正位反馈技术研究了多阶模态的主动振动控制[11]。

本文首先在传统FxLMS算法的理论基础上，根据反双曲正弦函数，提出了一种新的FxLMS算法，即FxasinhLMS算法；然后分别在Simulink和机械系统的力学自动分析(automatic dynamic analysis of mechanical system,ADAMS)中建立了FxLMS控制仿真系统和悬臂梁有限元模型，连接两者进行联合仿真。在联合仿真控制系统中，分别对FxLMS、Fair、FxatanLMS算法和本文提出的FxasinhLMS算法进行仿真测试。仿真测试结果证明了FxasinhLMS算法在悬臂梁振动主动控制应用中的有效性和优越性。

1 自适应滤波算法

1.1 LMS算法

LMS算法是线性自适应滤波器算法，其作用是调整滤波器的权系数。LMS算法以最小均方误差(mean square error，MSE)为判据，使期望信号与滤波器输出信号之差的平方的期望值最小[12]。基于LMS算法的自适应滤波器结构如图1所示。

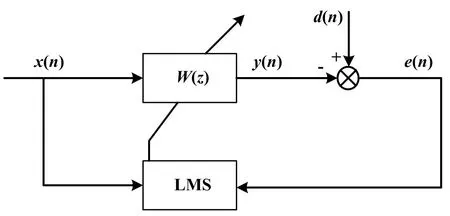
图1 基于LMS算法的自适应滤波器结构图

自适应滤波器W(z)采用有限脉冲响应(finite impulse response，FIR)结构。图1中：x(n)为输入信号；d(n)为期望信号；y(n)为滤波器输出信号；e(n)为误差信号；权系数矢量W根据最小均方判据调整。

对于FIR滤波器，n时刻的滤波器输出为:

(1)

式中：T为转置符；X(n)为n时刻的输入矢量；N为滤波器的阶数；wi(n)为n时刻第i个权系数,i=0,1,...,N-1。

根据图1，均方误差ε表示为：

ε=E[e2(n)]=E[d(n)-y(n)]2

(2)

将式(1)代入式(2)，可得：

ε=E[d(n)-WT(n)X(n)]2

(3)

从式(3)可以看出，均方误差是权系数矢量W的二次型函数，在均方误差达到最小时，权矢量W*达到最优。W*一般采用迭代算法来求解，常用方法是最速下降法，即：

(4)

式中：u为步长；W(n)为n时刻的滤波器权系数矢量；(n)为第n次迭代的梯度矢量；W(n+1)采用最速下降法，可以逼近最佳值。

对于LMS算法，第n次迭代的梯度矢量表示为：

(5)

用瞬时值代替式(5)中的数学期望，得到的梯度估计值称为瞬时梯度。则有：

(n)=-2e(n)X(n)

(6)

显而易见，瞬时梯度矢量是真实梯度矢量的无偏估计。此时，式(4)的迭代公式可写成：

W(n+1)=W(n)+ue(n)X(n)

(7)

为了确保算法的稳定性，步长的取值范围为：

(8)

式中：tr(R) 为输入信号自相关的迹，等于R对角线上的元素之和。

(9)

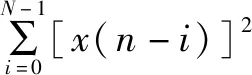
1.2 FxLMS算法

为了修正LMS算法的误差梯度估计值，在LMS的基础上增加了次路径模型。考虑到次路径的影响，为了确保系统的稳定性，需要对LMS算法的瞬时梯度估计作修正。xf(n)取代了LMS中的参考输入信号x(n)。xf(n)是参考输入信号x(n)经次路径S(z)滤波后得到的，所以这种算法被称为FxLMS算法。前馈FxLMS算法结构如图2所示。

图2 前馈FxLMS算法结构图

前馈FxLMS算法的步骤如下。

①采集输入信号x(n)。

②计算滤波器的输出信号u(n)：

(10)

式中：N为滤波器阶数。

③输入信号u(n)至次路径。

④计算滤波-x信号xf(n)：

(11)

⑤计算误差信号e(n)：

e(n)=d(n)-y(n)

(12)

⑥采用FxLMS算法，更新W(z)的权系数：

W(n+1)=W(n)-u×e(n)×xf(n)

(13)

2 改进的算法

FxLMS算法的迭代稳定性会受到误差信号e(n)的影响。为了保证算法的稳定性，本文提出一种改进方法，即设计一种新的非线性变换函数对误差信号e(n)作处理。

本文利用反双曲正弦函数对误差信号e(n)进行变换，提出FxasinhLMS算法。变换后的误差信号函数只有一个可调参数。其参数确定方法简单，避免了选择参数和估测阈值参数的麻烦。其误差变换函数为：

(14)

式中：α为系数;sinh-1为反双曲正弦。

将式(14)代入式(13)，则滤波器进行自适应更新的迭代公式为：

W(n+1)=W(n)-u×φ[e(n)]×xf(n)

(15)

使用反双曲正弦函数对误差信号进行非线性变换，使变换后的误差信号具有界二阶矩。反双曲正弦函数的特点是连续单调有界、奇对称，即当x→0时，f(x)→0，可以保证函数的收敛性和稳定性。假设X是一个符合正态分布的随机变量，定义Y=sinh-1(X)。因为反双曲正弦函数具有奇对称特性，所以其期望E(Y)=0。根据方差的计算公式，Y的方差为：

s(Y)=E[Y-E(Y)]2

(16)

(17)

由维纳滤波器原理可知，n时刻滤波器一定存在一个使得误差最小的最优解。因此，需要确定u的取值范围，以确保算法收敛。

假设w0是最优权系数矢量，w0xf(n)≈-d(n)，则偏差矢量ε(n)为：

ε(n)=w0-W(n)

(18)

在式(16)两端分别减去w0，有：

W(n+1)-w0=W(n)-w0-uφ[e(n)]xf(n)

(19)

ε(n+1)=ε(n)+uφ[e(n)]xf(n)

(20)

定义均方偏差σ(n)为：

(21)

式(20)两边取欧式2范数并求期望，得到：

(22)

考虑到：

(23)

(24)

假设：

εT(n)xf(n)=[w0(n)-w(n)]xf(n)≈-[d(n)-y(n)]=-e(n)

(25)

那么，式(23)可以写成：

Δ(n)=σ(n+1)-σ(n)<0

(26)

当算法收敛，步长应该满足下列条件：

(27)

3 悬臂梁振动主动控制联合仿真系统

3.1 建立FxLMS算法的控制系统

系统核心是基于FxLMS算法的自适应滤波器，采用Matlab Function进行FxLMS算法的编写。

控制仿真系统利用两个传递函数模块分别替代实际悬臂梁的主通道和次级通道。假设理想情况下次级通道和次级通道估计的传递函数相同。

3.2 建立ADAMS模型

本文以悬臂梁作为研究对象，借助ADAMS软件建立悬臂梁有限元模型。ADAMS的工作栅格为默认的笛卡尔坐标系，以steel作为悬臂梁材料。悬臂梁材料的长、宽、高分别为900 mm、25 mm、1 mm，密度为7.80×10-6kg/m。杨氏模量为2.07×105Pa，泊松比为0.29。悬臂梁受到外界刺激会发生变形，所以要把悬臂梁构件变成柔性体再作进一步的处理。本文采用ADAMS/ViewFlex建立柔性体，以代替原先的刚性体。

联合仿真需要ADAMS和Simulink两个软件进行数据通信：首先，定义ADAMS的输入变量为添加在悬臂梁根部和中间位置的两个控制力，定义ADAMS的输出变量为悬臂梁上五个标记点位置的变化；然后，采用varval()函数对定义的输入变量进行处理，使得输入变量与Simulink中的输入信号进行相关联；最后，完成ADAMS和Simulink这两个软件之间的数据通信。

定义ADAMS的输入输出变量后，将悬臂梁有限元模型通过Control Plant模块导出。

3.3 构建联合仿真系统

联合仿真的目的是实现机械系统和控制系统一体化。首先，在Matlab/Simulink中输入ADAMS模块。ADAMS模块如图3所示。

图3 ADAMS模块

将图3中的ADAMS模块与基于FxLMS算法的控制仿真系统相连接，得到机械系统与控制系统一体化的悬臂梁振动主动控制联合仿真系统。悬臂梁振动主动控制联合仿真系统如图4所示。

图4 悬臂梁振动主动控制联合仿真系统

在悬臂梁振动主动控制联合仿真系统中，输入信号为正弦信号。该信号的频率为一阶模态频率14 Hz。因为在低阶频率振动条件下，一阶模态存在的能量是最大的。一阶模态频率14 Hz是通过给定ADAMS模块一个扫频信号，然后对模块的输出信号作频谱分析所得到的。

联合仿真试验中，FxLMS算法通过跟随输入信号产生输出信号，利用其控制器产生控制力，再将其作用到悬臂梁模型需要消除振动的位置，与输入信号在该位置产生的响应相互抵消，从而实现降低悬臂梁振动。

4 仿真测试结果及分析

本文使用Matlab2016b、ADAMS2020这两个仿真软件，分别采用FxLMS、Fair、FxatanLMS和本文提出的FxasinhLMS算法在悬臂梁振动主动控制联合仿真系统中进行仿真。通过仿真获取每种算法的控制效果，并采用量化标准进行控制效果的比对，从而比较四种算法的性能。四种算法的仿真结果如图5所示。

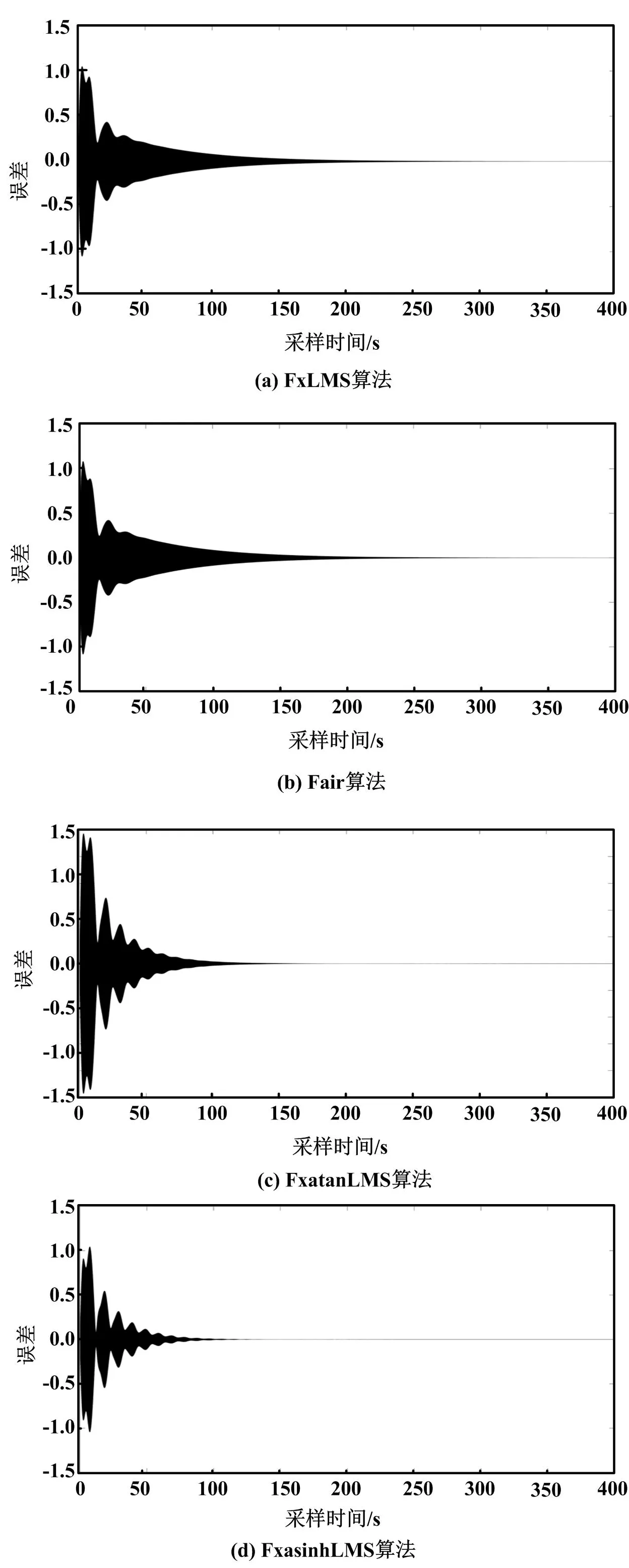
图5 四种算法的仿真结果

设定仿真试验参数如下：作为控制器的自适应滤波器阶数为8；Fair算法中，阈值c=5；FxasinhLMS算法中，α=3；FxLMS、Fair、FxatanLMS、FxasinhhLMS算法中，固定步长μ=0.0 000 001；采样频率为0.001 Hz；采样时间为400 s。

给定一个幅值1 V、频率14 Hz的正弦信号作为激励信号，利用FxLMS、Fair、FxatanLMS、FxasinhhLMS算法分别进行联合仿真。

对输入信号x和FxLMS、Fair、FxatanLMS、FxasinhhLMS四种算法进行频谱分析。频域结果如图6所示。

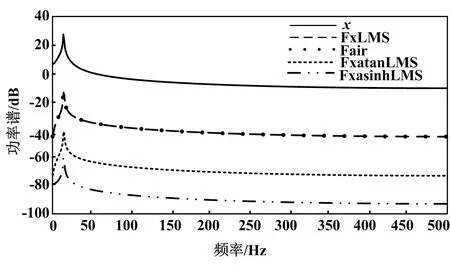
图6 频域结果

图6中，因为激励信号的频率是14 Hz，所以四种算法均在14 Hz时功率谱出现尖峰。当频率大于14 Hz后，随着频率增大，四种算法稳态误差的功率谱均呈逐渐衰减趋势。在频率为14 Hz时，四种算法对悬臂梁的振动都有衰减。该结果表明，四种算法均对悬臂梁振动有着一定的控制效果。其中，FxasinhhLMS算法的衰减效果最好。

主动振动控制应用中，算法的控制效果通常采用稳态误差和收敛速度这两个指标来评估。在本文的悬臂梁振动主动控制联合仿真系统仿真试验中，将系统达到稳定时对应的采样点作为起点，往后取100个采样点；以这100个采样点对应误差的平均值作为稳态误差指标，并以系统达到稳定时所用的迭代次数作为收敛速度指标。通过联合仿真得到的四种算法稳态误差和迭代次数如表1所示。

表1 四种算法稳态误差和迭代次数

由表1可知，基于FxasinhhLMS算法的仿真系统稳态误差为3.56×10-4，经过160 000次迭代达到稳定，其稳态误差和迭代次数均小于其他三种算法。经过比对，FxasinhhLMS算法的稳态误差减少了37%～52%、迭代次数减少了19%～57%。

5 结论

本文在Simulink中建立悬臂梁振动主动控制联合仿真系统，采用FxLMS算法作为自适应滤波算法，并基于传统FxLMS算法提出一种新的主动振动控制FxasinhLMS算法。该算法在原有的算法基础上对误差信号进行了改进，并利用反双曲正弦函数对误差信号进行非线性变换。分别将FxLMS、Fair、FxatanLMS、FxasinhhLMS算法在悬臂梁振动主动控制联合仿真系统中进行仿真。对比仿真结果可知，与FxLMS、Fair、FxatanLMS相比，FxasinhhLMS算法的系统稳态误差减小了37%～52%、迭代次数减少了19%～57%。FxasinhhLMS算法有效地解决了传统FxLMS算法无法平衡稳态误差和收敛速度的问题，使系统性能得到了明显的改善。