开关磁阻电机的自整定模糊-PID调速分析与验证

王 涛

(中国煤炭科工集团太原研究院有限公司，山西 太原 030006)

0 引言

开关磁阻电机[1-2](switched reluctance motor，SRM)越来越广泛地出现在各学者以及工程应用人员的视野中。SRM结构坚固，在起动时转矩大、电流小，因而工作效率与可靠性非常高，性能和经济指标优于普通的交流调速系统，多应用于高载重的大型机械中[3-5]。为了保证对电机的最大使用效率，开关磁阻电机磁路设计理念就是趋于饱和的[6-8]。由于开关磁阻电机特有的开关控制方式和特殊的双凸极结构，形成了参数高度非线性的电机。基于以上分析，采用传统比例积分微分(proportional integral differential,PID)控制策略很难取得较好的控制效果。

传统PID控制的特点包括鲁棒性强、可靠性高、算法相对固定与简单，在某些方面的应用非常广泛。但是，传统PID控制也有自己的局限性，如自适应能力比较匮乏。即电机的工作环境确定之后，其工作状态及一些参数就设成固定值，后续不会再改变。随着科技的日益发展，在生活和工程中对控制的要求越来越复杂，不确定性与智能化程度也越来越高。当前，要求控制技术同时具有高度时变与非线性的特点。传统的PID控制方法难以适应新的控制需求。

模糊控制是以模糊逻辑推理为基础，模仿相关资深专家决策过程的一种智能控制方法。该控制方式具有较强的鲁棒性，可以根据现场情况的需要适时调节PID控制器的参数，从而模拟相关控制人员的控制方式并进行优化。因此，模糊控制可以在一定程度上忽略相关参数的变化，不太依赖被控对象精确的数学模型。在开关磁阻电机中采用模糊控制方法[9-10]可以模拟有经验的专家的控制过程，及时调整 PID 控制器的参数。这种方法易于理解、实现简单，并且可以达到最佳的控制效果。

为了充分发挥二者的长处，本文将先进的模糊逻辑控制方法整合到传统的PID控制方式中，并对其进行优化，以在线实时整定 PID 控制器的参数。这种控制方法兼容了两种控制方法的优点，同时提高了系统的动态和静态响应特性，控制效果有显著提升。

1 开关磁阻电机数学模型

要研究开关磁阻电机的数学模型，需要作以下假设。

①磁路是不饱和的，即绕组的电感和电流没有直接联系。

②不计磁通的边缘效应。

③开关管的动作没有延时，瞬间完成。

④电机的转速不变。

根据基尔霍夫定律，开关磁阻电机的k相电压方程为：

(1)

式中：k=1,2,…,q；uk为第k相绕组的电压；ik为k相绕组的电流；Rk为k相绕组的电阻；Ψk为k相绕组的磁链。

在开关磁阻电机中，互感小到可以忽略，故磁链为要研究项的电流与自感与其他各相电流及转子位置结合的函数。

Ψk=Ψ(i1,i2,…,iq,θ)

(2)

式中：各项电感是相电流ik与转子位置角θ的函数。

根据力学定律，可得电机的机械运动方程：

(3)

(4)

式中:Ω为转子位置角对时间的导数；Te为电磁转矩；J为转动惯量；KΩ为摩擦系数；TL为负载转矩。

电机的磁共能对转子角度的偏导就是开关磁阻电机的电磁转矩，为：

(5)

式中:∂W(i1,i2,…iq,θ)为绕组的磁共能。

由于磁路高度饱和、涡流效应、磁滞效应和控制方式，会致使开关磁阻电机有强非线性。

2 自整定模糊-PID控制器

自整定模糊-PID控制器结构如图1所示。

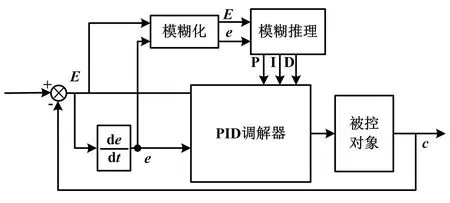
图1 模糊-PID控制器结构图

图1中：E和e分别是系统中的偏差和偏差变化率，实时满足PID参数自整定的要求。

自整定模糊-PID控制器利用模糊逻辑理论在线对PID参数进行实时调校。

2.1 输入和输出变量的隶属函数

标准三角形隶属函数如图2所示。

图2 标准三角形隶属函数

输入模糊变量是速度偏差E和速度偏差变化率e；输出模糊变量分别为比例、积分、微分参数KP、KI、KD。模糊语言集合由七个语言变量值组成，分别为负大NB、负中NM、负小NS、零ZO、正小PS、正中PM、正大PB。

2.2 参数自整定模糊规则的设计

首先确定参数比例、积分和微分与E和e之间的模糊关系。系统在运行状态下检测偏差及其变化率，再结合模糊逻辑控制规则对PID的三个参数进行实时在线校正。系统受到干扰时，这种自整定模糊-PID控制，可以适应E和e对控制器参数不同的需求，保证被控对象有优良的静态特性。

在不同E的情况下，被控对象对参数KP、KI、KD自整定情况有以下三种。

①当偏差E较大时，回调也相应变大。为了避免开始的瞬间偏差变大引起微分过饱和而导致系统运行超出预设的范围，且保持较好的快速跟踪到系统的能力，KP的取值应该稍大一些、KD应稍小一些。同时，在这种情况下取积分参数KI=0，以限制积分的作用，避免系统响应出现较大的超调。

②当偏差E的值介于较大和较小范围之间时，系统的超调值也会变小。此时，KP的值也应小一些，再适当地对KI和KD取值，以保证系统的快速响应。KP的大小对系统的响应速度影响很大。

③当偏差E较小时，考虑到系统的稳态性能，KP和KI的值应该稍大一些。同时，为了保证系统有较强的抗干扰性能、避免在设定值附近出现振荡，当e较小时，KD值可能大一些；当e较大时，KD值应该取小一些。根据上文所述，KP、KI、KD的不同修正规则表分别如表1～表3所示。

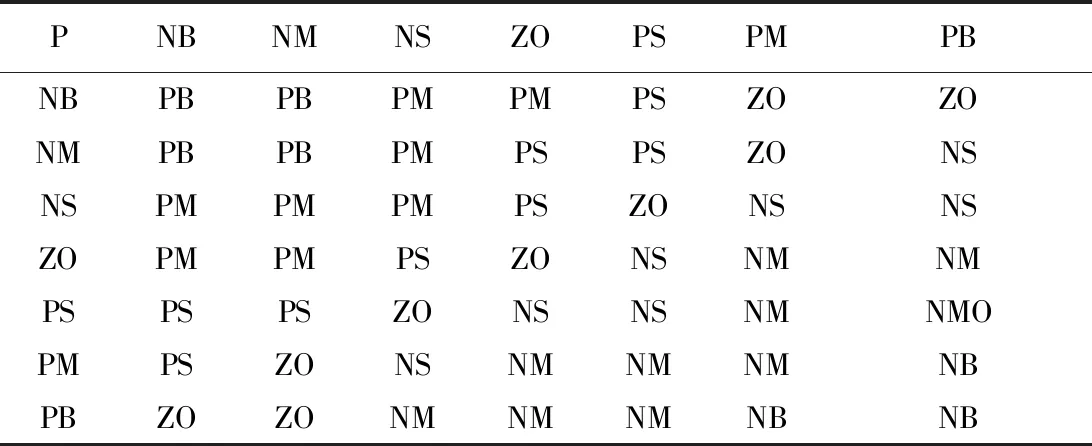
表1 KP修正规则表

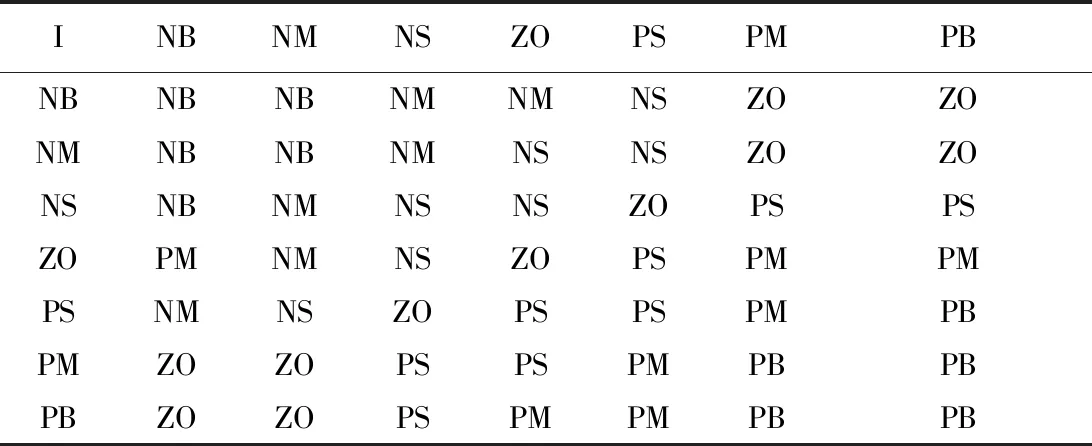
表2 KI修正规则表

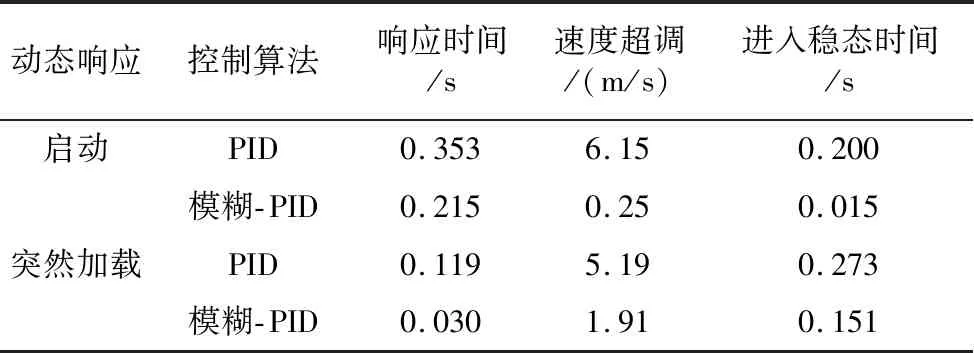
表2 两种控制算法的动态响应数据

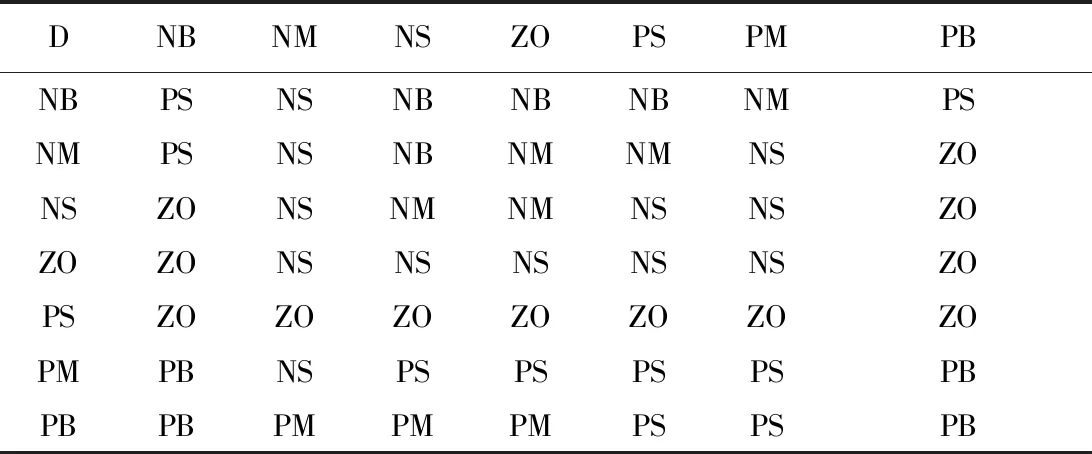
表3 KD修正规则表

KP、KI、KP的模糊整定规则曲面如图3所示。

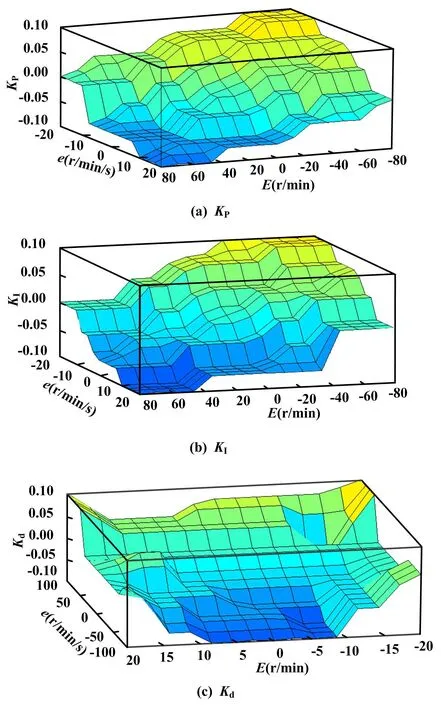
图3 模糊整定规则曲面

3 SRM系统仿真模型建立

开关磁阻电机模糊-PID调速整体仿真如图4所示。

图4 调速整体仿真框图

系统模块主要包括开关磁阻电机模块、功率变换模块、位置感应模块和模糊-PID控制模块。

系统采用六定子四转子结构的相关参数如下：惯性J为0.048 kg·m2，定子绕组Rs为0.055 Ω，摩擦系数F为0.018 N·m·s。

3.1 功率变换器模块

功率变换器采用三相不对称半桥电路，即CONVERTER模块。该模块有三个输入端，分别为两个输入电压(U+和U-)，以及开关管的控制信号输入端子G；有六个输出端口，分别与电机三相绕组相连。功率变换器模块结构如图5所示。

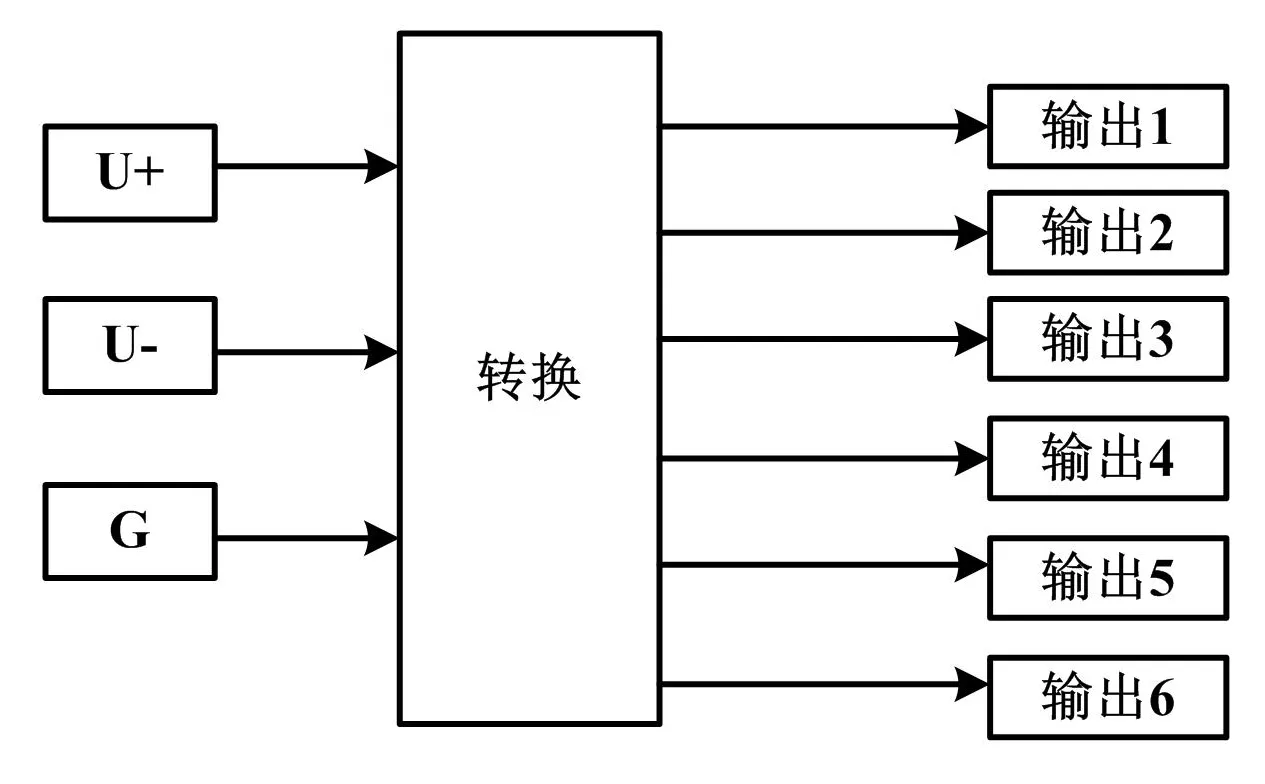
图5 功率变换器模块结构

3.2 位置感应模块

位置感应模块可以准确检测到转子的位置信息，使得功率变换器能够得到准确的开关信号。本文设定其开通角为45°、关断角为85°。位置感应模块如图6所示。

图6 位置感应模块示意图

3.3 模糊-PID模块

自整定模糊-PID模块如图7所示。

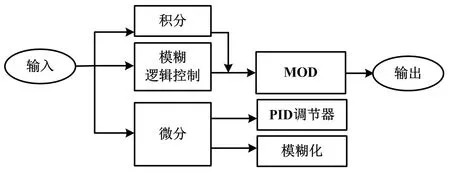
图7 模糊-PID模块示意图

4 仿真结果分析

开关磁阻电机空载时，在传统的PID控制器控制和模糊PID控制下，电机对阶跃信号的转速响应曲线如图8所示。

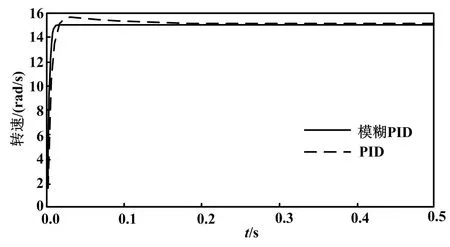
图8 转速响应曲线

PID控制器参数为KP=1.04、KI=20、KD=0.1。由图8可知：传统PID控制在0.3 s左右才进入稳态，系统超调非常大；改进后的自整定模糊-PID控制算法转速响应快到0.03 s时就进入稳定状态，超调小到可以忽略。

平衡状态下突然加负载的速度响应曲线如图9所示。由图9可知，平稳状态下，电机运行稳定后在0.6 s时突然加负载，传统PID控制法电机转速大幅度下降并且需要较长时间才能回到稳定状态，而改进后的自整定模糊-PID控制方法在施加负载后电机转速经过微小波动便恢复到稳态。改进后的控制方法恢复时间较短，表明该控制系统有较强的抗干扰性和鲁棒性。

图9 平稳状态下突然加负载的速度响应曲线

经过大量的测试后，两种算法的动态响应数据如表2所示。分析表2可知，改进后的自整定模糊-PID控制器在动态响应速率、超调量和进入稳态时间方面，控制性能明显优于传统PID控制。

5 结论

本文提出了开关磁阻电机传统PID控制进行模糊逻辑控制的改进方法。由于开关磁阻电机高度非线性特性，在启动和抗干扰等方面控制效果非常差。本文改进的自整定模糊-PID控制器按照模糊逻辑整定规则，可以实时地对PID参数进行合适的调整。仿真验证结果表明，对于高度非线性特性的开关磁阻电机，采用改进模糊-PID控制策略，其控制效果明显优于传统PID控制方法，超调幅度小，动态响应快速，稳态精度高。由此证明，改进的控制系统有比较强的抗干扰能力和鲁棒性。