对滑轮悬挂物体问题利用角动量定理和刚体定轴转动定律的分析
范 继 苏晓莉
(华中科技大学物理学院 湖北 武汉 430074)
1 引言
角动量定理与刚体定轴转动定律是大一学生在学习“大学物理”力学部分时的难点内容[1~4].由于在中学阶段学生们并没有接触过相应的知识点,因而在大学阶段的学习过程中很容易对相关概念的理解及应用产生较大误解.特别在学习完刚体的角动量定理后,学生们处理滑轮悬挂物体问题时有了多种解法,这时反而容易对物理概念混淆不清.质点的角动量定理表述为,质点对任一固定点的角动量的时间变化率,等于质点所受的合外力对该固定点的力矩[5].刚体定轴转动定律可表述为,在定轴转动中,刚体受到的所有外力对转轴的合外力矩等于刚体对该轴的转动惯量和角加速度的乘积[5].滑轮悬挂物体问题常常可利用这两个知识点进行分析,然而到底应该利用角动量定理还是利用刚体定轴转动定律进行求解,部分学生因对物理过程判断不清而用错公式.尽管角动量定理与刚体定轴转动定律都能用来求解此类问题,但其相应的问题分析方式并不相同.这使得学生们在分析相关物理过程时容易感到困难,不利于他们形成正确的知识体系.同时,“大学物理”课堂的新手教师们在初次遇到个别学生对此类问题的解答时也很容易误判.为此,本文针对角动量定理与刚体定轴转动定律应用于滑轮悬挂物体问题进行了详细的说明,分析了错误应用物理概念却得到正确结果的原因.本文对滑轮悬挂物体这一类问题的特殊性进行了阐述,最后说明了利用这种特殊性进行求解以简化解题的过程,但不推荐学生采用这种分析方式.本文强调在授课过程中应尽可能做到让学生们正确理解基本物理概念,让他们明确可能存在的错误的起因,以帮助学生对物理过程进行理解.
2 滑轮悬挂物体问题的一道典型例题及其经典解法
在学习刚体定轴转动定律时,通常会给学生们讲授如下典型例题:
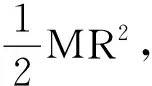
这道题目涉及一个刚体(滑轮)的定轴转动与质点(物体)线运动的混合,在分析此类问题时,我们一般采用刚体的定轴转动定律来分析刚体的运动,而对线运动的物体一般则采用牛顿第二运动定律去分析.根据题意,我们首先可对系统中的每个研究对象分别进行受力分析,如图1所示.
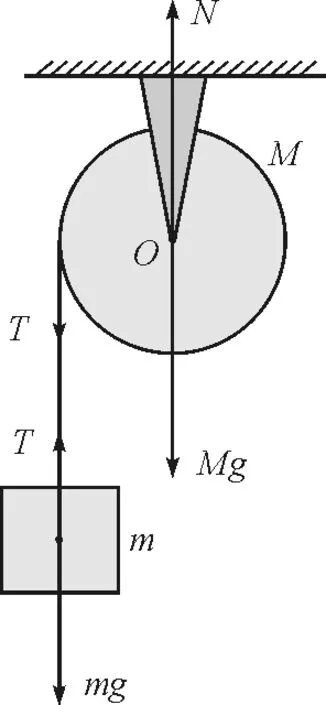
图1 滑轮悬挂物体的受力分析图
悬挂的物体m受到两个力的作用,即重力mg与绳的拉力T.滑轮受到自身重力Mg,支撑点的支撑力N以及绳的拉力.很明显,滑轮的重力与支撑点的支撑力均通过其轴心,故它们不对滑轮产生力矩.有了上述分析过程后,可定义沿铅垂线竖直向下为正方向.对悬挂的物体m,根据牛顿第二运动定律,可得
mg-T=ma
(1)
式中,a为悬挂物体下落的加速度.对滑轮M,运用刚体定轴转动定律可得
TR=JMβM
(2)
式中,JM为滑轮对过O点且与纸面垂直的转轴的转动惯量,βM为滑轮的角加速度.由于绳子与定滑轮之间无相对滑动,因此,线加速度与角加速度存在如下的关系
a=RβM
(3)
联立式(1)、(2),以及式(3),可得
(4)
上述解法是在授课过程中较为常用的一种解题方法.在课程进行到刚体转动的机械能守恒时,亦可利用机械能守恒进行求解.由于该解法的分析超出本文范围,这里不作讨论.
3 学生常犯的几种错误
学生在遇到上述问题进行求解时,有几种常犯的错误,但最终却都得出了正确的答案,这需要引起教师们的重视.下面我们将进行详细阐述.
3.1 利用角动量定理时存在的错误概念
有学生在解题时会直接给出这样的解答过程:
因为绳和滑轮之间无滑动,所以根据刚体角动量定理的微分形式,可以得出
(5)
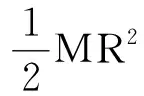
(6)
由上式可以解得与式(4)相同的结果.
这种解题方法是否正确呢?所谓刚体,就是在任何情况下,大小和形状都不会发生变化的物体.很显然,根据刚体的定义[5],此类滑轮悬挂物体问题中滑轮与物体构成的系统并不是刚体,因而不能利用刚体角动量定理进行解题.虽然最后结果是对的,但该学生对刚体的概念理解错误.
那到底能否应用角动量定理进行求解?答案是肯定的,我们可从质点系角动量定理进行分析(刚体可以看成质点系).质点系角动量定理可描述为质点系对惯性系中某给定参考点的角动量的时间变化率,等于作用在该质点系上所有外力对该给定参考点的总力矩.对于图1中所描述的滑轮与物体组成的系统而言,虽然滑轮是围绕转轴在做定轴转动,但是所悬挂的物体是做线运动.如果将O点视为整个系统的给定参考点,物体m看成一质点,则整个质点系的角动量L可写为
L=r×p+JMω
(7)
式中,r为物体m到O点距离,p为物体m的动量,ω为滑轮转动的角速度.
我们对整个系统的运动再次进行分析,如图2所示,假设在t时刻物体m运动到某一位置时,它拥有垂直向下的速度为v.因此物体m对于O点角动量r×p可表示为
r×p=rpsinθe=
(8)
式中,e为垂直于纸面向外的单位矢量.滑轮的角动量JMω可表示为
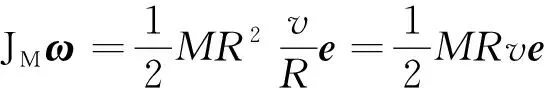
(9)
将M与m看作一个系统,系统所受外力包括M所受的重力与支撑力,以及m所受重力.其中,M所受的重力与支撑力是经过整个系统的给定参考点的中心,因此它们不产生力矩,即力矩为零.m所受重力对O点的力矩为
M=r×F=rmgsinθe=mgRe
(10)
方向为垂直于纸面向外.结合式(7)~(10),运用角动量定理的微分形式Mdt=dL有
(11)
可见式(11)与式(5)相同,对等式两边同时做积分可得与式(4)相同的结果.
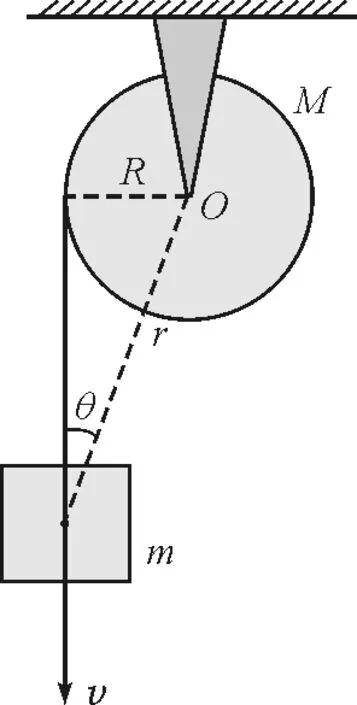
图2 利用质点系角动量定理求解的速度分析图
由此可看出,虽然利用刚体角动量定理和质点系角动量定理得到了相同的结果,但是对其物理过程的理解是完全不同的.利用质点系角动量定理求解是正确的,而利用刚体角动量定理则存在对刚体定义的错误理解,错误的概念运用得到正确的结果,这由一系列特殊的几何关系所导致的,后面我们还会进行详细的分析.
3.2 利用刚体定轴转动定律时存在的错误概念
也有学生在解题时会直接给出这样的解答过程:
因为绳和滑轮之间无滑动,所以利用刚体定轴转动定律M=Jβ可得
(12)
由上式可解得
(13)
再结合式(3)可以得到与式(4)相同的结果.
虽然得到了正确的结果,但是这种解题思路是否正确呢?首先根据转动惯量的形式,式(12)认为物体m与滑轮M是绕O点做转动的,同时式(12)也认为物体m与滑轮M有相同的角加速度βM,这显然是不正确的.如果将m和M看作都是绕O点做转动,那么由于转动的半径不同,他们的角加速度是不相同的,所以根据刚体定轴转动定律列出的式(12)是不正确的.为什么不正确的表达式会得出正确的答案呢?
伯克利物理学教程第一卷《力学》(科学出版社,1979年,P339)写道:“因为转轴的方向被限制固定在空间,而且相对于物体也是固定的,所以物体的惯量特性相对于轴是不变的.”刚体的定轴转动定律M力矩=Jβ可理解为角动量定理的一种特殊情况的表达方式,它所强调的是整个刚体围绕某一固定的转轴在做转动时的角加速度与外力之间的关系[6].对于图1所描述的滑轮与物体组成的系统而言,虽然滑轮是围绕转轴在做定轴转动,但由于物体做线运动,因而它们整体的运动情况并不是围绕某一转轴在做定轴转动.但是,这类问题是否可以整体利用刚体定轴转动定律进行求解呢?我们知道刚体是一种理想的模型,在转动中没有形变.对于做线运动的质点而言,它可被看成一种很特殊的刚体,所以可以用刚体的定轴转动定律来分析质点的线运动.
此时利用刚体定轴转动定律求解,强调的是整个系统绕固定的转轴旋转.在图2所示的求解方式中,我们将t时刻的m看成围绕O点进行转动,此时它的转动惯量可写为
(13)
若物体m下落的加速度为a,则它在t时刻绕O的切线方向的角加速度可表示为
(14)
若将M与m看做一个系统,在t时刻围绕O点做定轴转动,则系统只受到物体m重力的力矩作用,利用刚体定轴转动定律,我们可以得到
mgR=JMβM+Jmβm
(15)
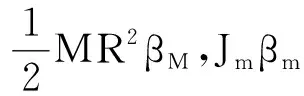
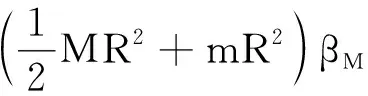
(16)
再结合式(3),可以解得
(17)
则在t时刻,物体m下落的速度可由v=at求得与式(4)相同的结果.
可以发现式(12)与式(16)是等价的,这是由一系列特殊的几何关系所导致的.所以此类问题是可以用刚体定轴转动定律进行求解的.但是对其物理过程的理解是需要仔细推敲的.在给学生讲述时要特别强调不能单纯地利用刚体定轴转动定律得出式(12),而应该利用几何关系一步一步地推导出式(16).因为严格讲来,式(16)已不是“刚体转动定律”了,因为它是两个刚体组合而成的刚体,一旦这种组合刚体没有了相互作用力,式(16)就不成立了.
4 推广分析
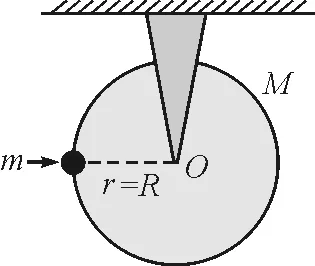
图3 利用临界状态分析法示意图
为什么这种根据初始(临界)状态列出的方程可以解得正确的结果?首先,在这样一个系统中,m的线加速度以及M对O点的角加速度为一定值,它们并不随着时间而发生改变,所以无论在系统的任何阶段,只要能够求出其在任意时刻的线加速度或者角加速度就可以求出下落速度与时间的准确关系.其次,在我们只利用刚体定轴转动定律求解时,在不同的位置m对O点的转动动量不同,如式(13)所示.m的运动过程中对O点的角加速度也在时刻变化,如式(14)所示.我们代入一系列典型值利用MATLAB进行计算,可得从图3时刻开始1 s内m对O点的转动惯量以及角加速度的结果,如图4所示.我们可以发现在下落过程中m对O点的转动惯量以及角加速度在不断的变化,且这种变化是非线性的.但是如果将m对O点的转动惯量以及角加速度相乘,我们可以发现有关物体位置信息的变量θ就会被约掉,此时整个系统的Jβ就与临界状态时的表达式完全一样,为一定值,如图5所示.

图4 滑轮所悬挂物体的角加速度与转动惯量分析

图5 滑轮所悬挂物体的角加速度与转动惯量乘积的分析
可以得出这样的结论,在滑轮悬挂物体这类问题中,物体与滑轮相对于O点的转动惯量与它们相对于O的角加速度乘积之和为一定值.那么,利用这种特殊性能否为我们的解题带来一定的方便呢?下面我们将一个滑轮与一个物体的情况推广至两个滑轮与两个悬挂物体的情况,如以下典型例题:

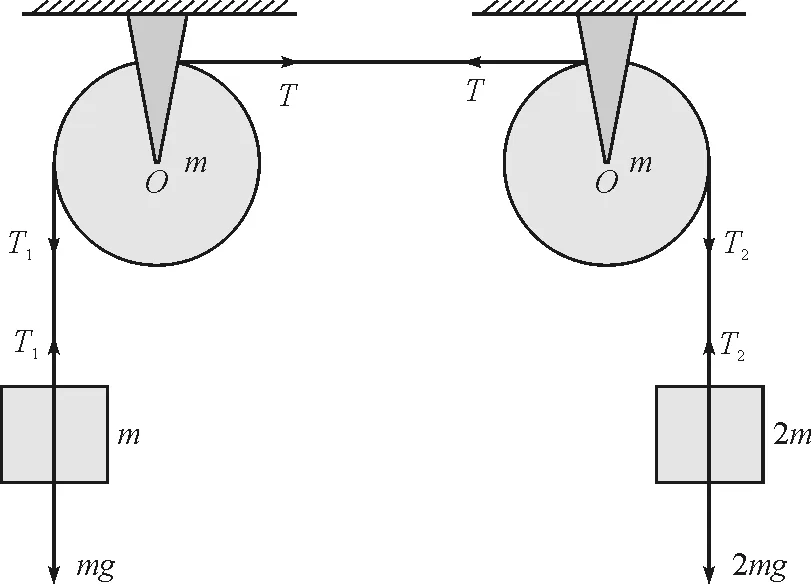
图6 两个滑轮悬挂两个物体的受力分析图
此题的典型解法是首先针对两个滑轮分别利用刚体定轴转动定律进行分析,由于右边的物体会向下运动,左边的物体会向上运动,连接两物体的绳水平向右运动,设水平向右为正方向,因而对滑轮和物体分别进行受力分析(图6)后可得如下结论.
对左边滑轮
(18)
对右边滑轮

(19)
对悬挂的物体分别利用牛顿第二运动定律.
对左边物体
T1-mg=ma
(20)
对右边物体
2mg-T2=2ma
(21)
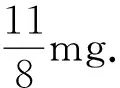
对于此类滑轮物块问题,因为所悬挂的物体对相近的滑轮中心的转动惯量与角加速度乘积为一定值,我们利用前述的转动惯量与角加速度乘积之和为一定值的特殊性进行解题,看是否会得到正确的结果.首先,因为右边的物体重量大于左边的物体重量,所以整个系统运动时右边悬挂的物体向下运动,左边悬挂的物体向上运动.我们首先认为在最初阶段,右边悬挂的物体贴近右边的滑轮,把它当成一质点来对待,根据其运动方向设定沿铅垂线向下为y轴正方向,水平向右为x轴正方向,此时右边滑轮与右边物体组成的系统应用刚体定轴转动定律可得
(22)
若将左边的悬挂物体当成一质点来处理,然后在最末时刻它必将运动至左边的滑轮边缘处,根据其运动方向,设沿铅垂线竖直向上为y轴正方向,水平向右为x轴正方向,此时左边滑轮与左边物体组成的系统可利用刚体定轴转动定律可得

(23)
将式(19)与(18)相除可得
(24)
求解可得两绳之间张力为
很明显,利用这种特殊性求解多个滑轮与多个悬挂物体组成的系统问题时是比较简便的.但是有一点必须明确指出,因为在整个运动过程中,有关物体位置信息的变量θ会在计算过程中被约掉,所以在利用物体贴近滑轮时所得到悬挂物体对相邻滑轮中心的转动惯量以及角加速度乘积的表达式,在任意时刻都是相同的,正是因为这一点我们可以利用这种方法进行求解以简化计算.在授课过程中我们必须让学生对物理概念有清楚的理解,因而不推荐学生采用此种解法.这里介绍该方法仅为了让大家认识到滑轮悬挂物体问题的特殊性.
5 结束语
综上所述,在求解滑轮悬挂物体这一类问题时,学生容易对一些物理概念产生误解,但是这种错误的认识却能得到正确的答案,这需要引起教师们的重视.这种错误认识能得到正确答案的具体原因在于所悬挂物体对滑轮中心转动惯量与角加速度的乘积与物体所处的位置无关,这种巧合完全是由这类题目几何关系的特殊性造成的.在多个滑轮与物体所组成的系统中,我们利用这种特殊性进行解题可简化分析与计算.但是在教学过程中一定要让学生对物理概念有清晰的理解,以免因这种特殊性的存在让学生们对物理概念认识错误.

