基于Apriori关联规则算法提高雷达测速精度研究

田珂，常华俊

(中国人民解放军63861部队，吉林 白城 137001)

靶场试验中，初速雷达相对火炮的布站位置决定着雷达的测速精度，而布站位置更多的是取决于参试人员的参试经验，具有一定随意性。为了更加科学准确地选择雷达布站的位置，提高雷达测速精度，选择采用Apriori关联规则算法从大量的历史试验数据中挖掘出能保证雷达测速精度最高时的布站位置。因为关联规则适用于挖掘出影响某一指标的其他因素，可以为装备试验提供重要依据[1]。当雷达、火炮和外界因素均良好时，影响初速雷达测速精度的因素就是雷达相对火炮的布站位置，所以选择把雷达相对火炮的布站位置作为关联规则的左侧规则，弹丸的炮口初速精度作为关联规则的右侧规则，利用Apriori关联规则算法挖掘出测速精度最高时两者之间的频繁项集，为科学合理的选择雷达布站位置提供重要依据。通过实测数据进行实验验证的结果表明，利用挖掘出的强关联规则进行雷达布站，测试出的弹丸初速的精度有明显提升。

1 Apriori关联规则算法

Apriori算法是最常用的关联规则挖掘算法，是由Rakesh Agrawal博士和Ramakrishnan Srikant博士于1990年联合提出的[2]，是一种逐层搜索的迭代方法。其核心思想是通过连接产生候选项及其支持度，然后通过剪枝生成频繁项集。具体的原理是，如果一个项目是频繁的，那么它的所有子集都是频繁的；同理，如果一个项目是非频繁的，那么它的所有子集也都是非频繁的。

1.1 关联规则和频繁项集

项集A和项集B同时发生的概率称为关联规则的支持度；如果项集A发生，则项集B发生的概率称为关联规则的置信度。支持度和置信度是衡量关联规则的两个重要指标[3]。支持度和置信度通常会设置一个阈值，分别为最小支持度阈值和最小置信度阈值。最小支持度表示项目集的最低重要性，最小置信度表示关联规则的最低可靠性[4]，只有同时满足最小支持度阈值和最小置信度阈值的关联规则被称为强规则，这也是Apriori关联规则算法挖掘的目标。

1.2 Apriori关联规则实现过程

Apriori关联规则算法是找出存在于事务数据集中的最大频繁项集，然后利用得到的最大频繁项集与预先设定的最小支持度阈值和最小置信度阈值生成强关联规则。Apriori关联规则算法运行的具体过程如图1所示。

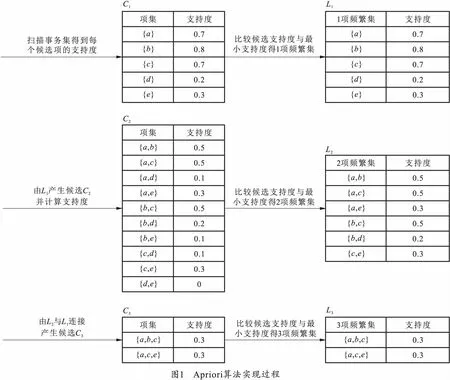
1)努力搜索找出事务数据集中所有的频繁项集，这些频繁项集的支持度必须大于等于给定的最小支持度阈值，直到找到最大频繁项集为止。具体分为连接步和剪枝步，连接步的最终目的是找到最大频繁项集，剪枝步就是剔除所有非频繁的候选项集[5]。

2)由频繁项集产生强关联规则，在过程1)中未达到预设的最小支持度阈值的项集已被剔除，剩下的就是同时满足最小支持度阈值和最小置信度阈值的强关联规则[6]。

2 雷达布站规则挖掘

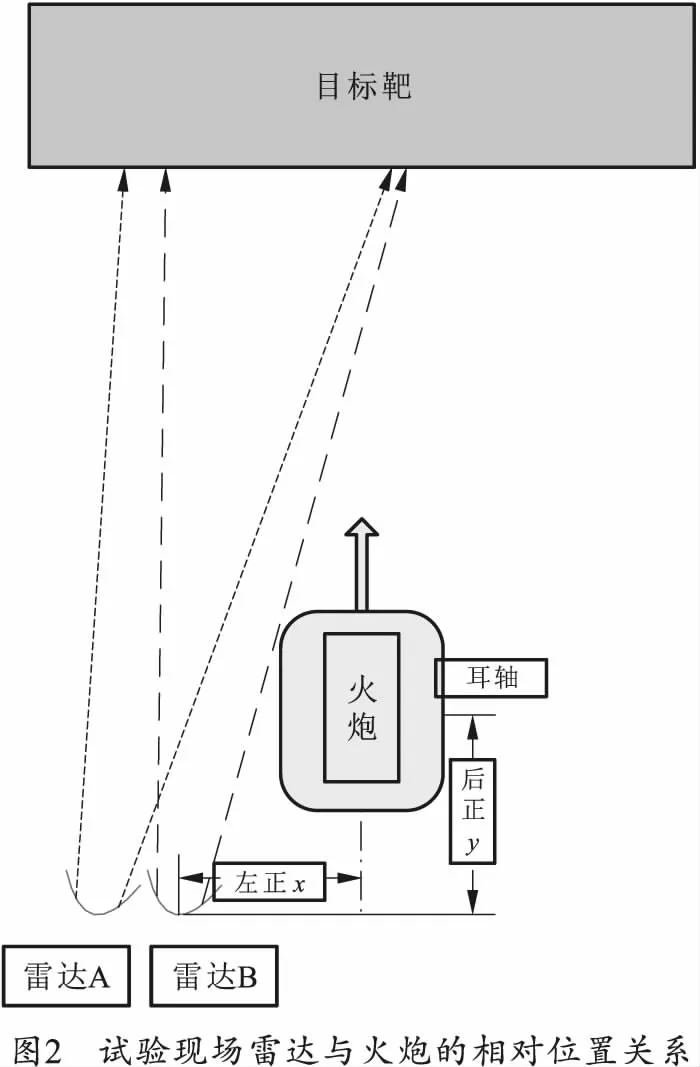
初速雷达参与试验时，在雷达、火炮以及所有外界因素均良好的情况下，雷达相对火炮的布站地点直接影响雷达的测速精度，其中影响最大的3个因素就是雷达距离火炮的后正、左正和下正，而同一试验中雷达相对火炮的下正是固定不变的，只有后正和左正会因雷达布站的不同而发生变化，所以只研究雷达相对火炮的后正和左正对弹丸初速精度的影响。试验时，雷达与火炮及射击的目标靶之间的关系如图2所示，由于雷达通常架设在火炮的侧后方，雷达相对火炮的后正是指火炮耳轴到雷达天线面的水平垂直距离y，雷达相对火炮的左正是指雷达天线面的中心点到火炮身管后方延伸线的水平垂直距离x，雷达相对火炮的下正是指雷达天线面中心点距离地面的垂直距离减去火炮耳轴距离地面的垂直距离z。为了充分展示利用Apriori算法挖掘出雷达后正、左正与测速准确性之间关系的过程，选取某型初速雷达历史实测数据进行挖掘，具体如表1所示。

续表1

从图2中可以看出，雷达A在雷达B的左侧，短虚线之间是雷达A辐射的电磁波的照射范围，长虚线之间是雷达B辐射的电磁波的照射范围，火炮发射的弹丸在雷达B的电磁波束中的飞行时间要长于在雷达A的电磁波束中的飞行时间，所以雷达B测试的弹丸的径向速度更加完整，拟合递推出的初速数据更加准确，所以雷达B的测试状态要好于雷达A，因此把雷达B的初速数据作为对比数据。表1中包含了弹序、雷达A的后正和左正的布站坐标、雷达A和雷达B测试的弹丸初速、雷达A相对于雷达B的误差，以及雷达A相对雷达B的初速准确性。根据初速雷达本身的测速精度要求，试验当中两台雷达的测速误差最多不能大于2‰，所以根据表1把两台雷达的误差设置为：如果雷达A相对雷达B的误差绝对值小于等于雷达B初速的1‰，则雷达A初速的准确性设为“很好”；如果雷达A相对雷达B的误差绝对值大于雷达B初速的1‰，且小于等于雷达B初速的1.5‰，则雷达A初速的准确性设为“好”；如果雷达A相对雷达B的误差绝对值大于雷达B初速的1.5‰，且小于等于雷达B初速的2‰，则雷达A的初速准确性设为“一般”；如果雷达A相对雷达B的误差绝对值大于雷达B初速的2‰，则雷达A的初速准确性设为“差”。

从表1中可以看出，雷达A的布站地点与雷达A测速准确性之间是存在一定关联关系的，有的是强关联，有的是弱关联。为了排除偶然性，挖掘出一般规律，选择利用Apriori算法挖掘出雷达A的布站地点与雷达A测速准确性之间的强关联规则，为该类型试验进行雷达布站提供标准的布站模式[7]。根据表1中雷达A的后正和左正具体数据，选择把雷达A的后正和左正按照表2的形式进行区间分类。

表2 雷达A后正和左正不同范围对应的类别

将雷达A的后正和左正当作关联规则的左侧规则，将雷达A测速的准确性当作关联规则的右侧规则，构建出雷达A相对火炮的后正和左正与雷达A测试弹丸初速准确性之间的对应关系[8]。将表1作为历史数据，利用Apriori关联规则算法挖掘出雷达A的后正、左正与测速准确性之间的关系时，选择把支持度设为0.1，置信度设为0.95，通过挖掘得到了12条关联规则[9]，如表3所示。

表3 Apriori关联规则算法挖掘结果

从表3的结果可以看出，所有关联规则的支持度均为10%，置信度均为100%，都符合所设置的最小支持度阈值和最小置信度阈值，但是只有提升度大于1的强关联规则是有效的[10]。结合开展试验的实际情况可以确定，只有强关联规则{A6,B3}⟹{很好}和{A3,B2}⟹{很好}是符合实际需求的，即这两个规则才是挖掘的目标规则。即当后正处于(7,8]之间、左正处于(4,5]之间时，或者后正处于(4,5]之间、左正处于(3,4]之间时，雷达A的测速准确性为“很好”的可能性为10%，这种情况发生的可能性[11]为100%。这两种规则的使用情况分别为：因为雷达与火炮的射角是一样的，当火炮的射角不是很高时，为了确保雷达波束能够长时间照射到弹丸，雷达的后正和左正都要大一些，此时采用关联规则{A6,B3}⟹{很好}进行雷达布站；当火炮的射角很高时，雷达就要离火炮近一些，保证弹丸一出炮口就进入雷达波束并在雷达波束中飞行时间长一些，就要采用关联规则{A3,B2}⟹{很好}进行雷达布站。

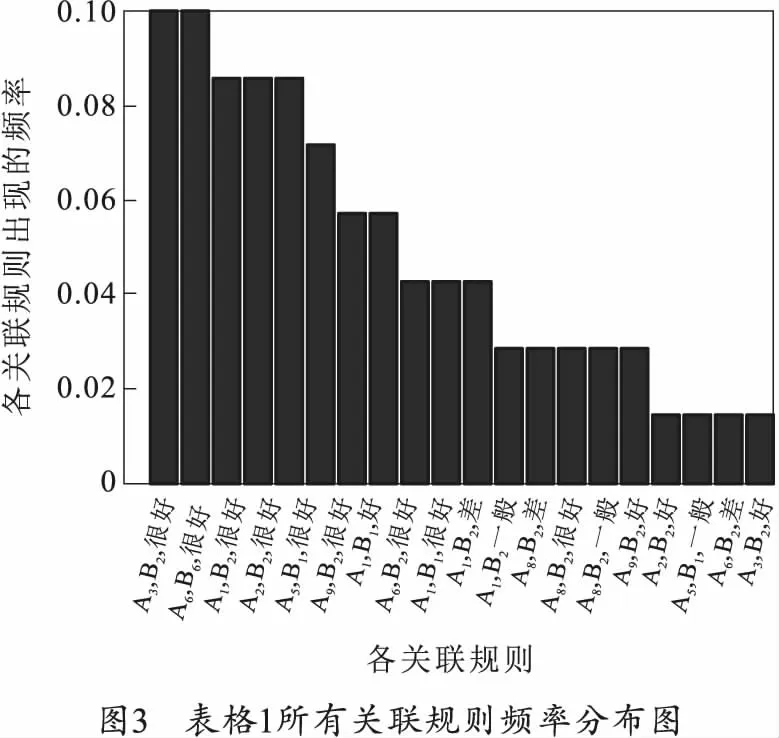
实际上，表1中所列举的是某型试验中雷达A和雷达B共同测试的70发初速数据，每7发为一组，从第1组数据到第10组数据，雷达A相对雷达B的平均相对误差分别为0.113%、0.063%、0.157%、0.079%、0.041%、0.081%、0.099%、0.083%、0.088%、0.207%。关联规则{A6,B3}⟹{很好}对应的是第2组数据，雷达A对雷达B的平均相对误差为0.063%；关联规则{A3,B2}⟹{很好}对应的是第5组数据，雷达A对雷达B的平均相对误差为0.041%，这两个规则的平均相对误差均小于1‰，也是所有组数据中平均相对误差最小的，也充分证明了挖掘出的两个强关联规则是准确可靠的。绘制表1各项事务频率分布的可视图，如图3所示，可以看出关联规则{A3,B2}⟹{很好}、{A6,B3}⟹{很好}出现的频率是最高的，这也更充分说明挖掘出的两个关联规则是准确可信的。

3 实验验证

实验验证选择在RStudio软件环境下进行数据分析、统计建模及数据可视化。为了验证所挖掘出的关联规则的准确性，针对同一试验任务，利用规则{A3,B2}⟹{很好}进行布站，对得到的测试数据进行验证。测试数据如表4所示，表中误差指的是雷达A相对于雷达B的误差。雷达A与雷达B测试的初速数据的实测值关系曲线如图4所示。

表4 测试数据

从表4和图4可以看出，当采用关联规则{A3,B2}⟹{很好}进行雷达布站时，测试的7发弹丸的初速数据中，雷达A相对雷达B的准确性为“很好”的可能性为57.1%，准确性为“好”的可能性为42.9%，两者加起来的可能性为100%，没有准确性为“差”和“一般”的结果，而且支持度明显大于10%。雷达A相对雷达B测试的7发弹丸的初速数据的平均相对误差为0.075%，远小于1‰，整体的准确性为“很好”，同时也小于表3中除了挖掘出的两个关联规则以外的数据的平均相对误差，表明按照所挖掘出的关联规则进行雷达布站，有效提高了雷达的测速精度。

4 结束语

由于利用初速雷达测试弹丸初速的试验中，确定雷达布站地点依靠的是参试人员的经验，导致雷达布站具有一定随意性，雷达的测试准确性时好时坏，所以选择将雷达的布站地点与测试准确性对应起来，将布站地点作为左侧规则、测试准确性作为右侧规则，利用Apriori算法从历史数据中挖掘出当雷达测试准确性为“很好”时对应的布站地点，然后按照挖掘出的雷达布站地点进行试验并获取到实测初速数据。经过计算发现获取的实测初速数据的平均相对误差小于1‰，整体的准确性为“很好”，没有“一般”和“差”的情况，说明所采用的方法能够提升雷达的测试精度。