线圈式电磁炮放电回路参数研究

张铭豪，曹增强,2，郑国，袁昕宇，李想，杜蒙

(1.西北工业大学 机电学院，陕西 西安 710072；2.陕西大工旭航电磁科技有限公司，陕西 西安 710100)

电磁发射技术是一种利用电磁能给物体提供推动力的发射技术，与传统的发射器相比，电磁炮具有发射速度高，易于控制，隐蔽性好等诸多优点[1-2]。当前，在电磁发射领域，主要有导轨炮、线圈炮和重接炮3种类型的电磁炮[3]，其中线圈炮具有结构简单、可发射大质量载荷、电枢与发射器之间无摩擦等优点，具有非常广阔的应用前景，是当前国内外研究的热点[4-5]，追求电磁炮更大的发射动力和炮弹的发射速度一直是研究人员关注的重点[6]。针对发射过程的建模数值仿真是支撑电磁炮技术发展的重要基础之一[7]，向红军等[8]介绍了电磁感应线圈发射器的工作原理，建立了感应线圈发射器的数学模型；熊敏等[9]建立了线圈的温升模型，为后续抑制温升、实现电磁线圈发射器小型化奠定了基础；国伟等[10]对电磁线圈炮弹丸初速、最佳触发位置、单线圈效率之间的关系进行了仿真分析。由于线圈放电时间极短，其持续时间从几百微秒到几毫秒[11]，通过理论计算很难求得线圈放电过程的磁场分布和电流变化。当前针对电磁线圈炮的建模仿真研究主要集中在二维平面建模上[12-14]，且对线圈炮电路系统的研究较为少见。为了提高电磁发射能力，对电磁发射电路系统的设计和线圈炮试验提供参考，笔者采用离散化有限元方法，借助ANSYS Maxwell在3D瞬态求解器建立线圈发射过程的耦合模型进行研究，并通过发射试验对仿真结果进行了验证。

1 线圈式电磁炮发射原理

1.1 线圈式电磁炮基本原理

电磁炮发射过程是一种复杂的瞬态多物理场作用过程，包括电场、磁场、温度场和结构场等共同耦合作用。线圈式电磁炮基本原理如图1所示。交流电升压、整流后变为直流电对电容充电，到达指定电压后，放电晶闸管控制放电回路导通，此时电容瞬间释放的大脉冲电流流经加载线圈形成脉冲磁场，变化的磁感线穿过感应线圈产生变化的磁通量，使感应线圈中产生与加载线圈同轴反向的涡流，瞬时磁场和涡流相互作用产生电磁斥力将炮弹发射。

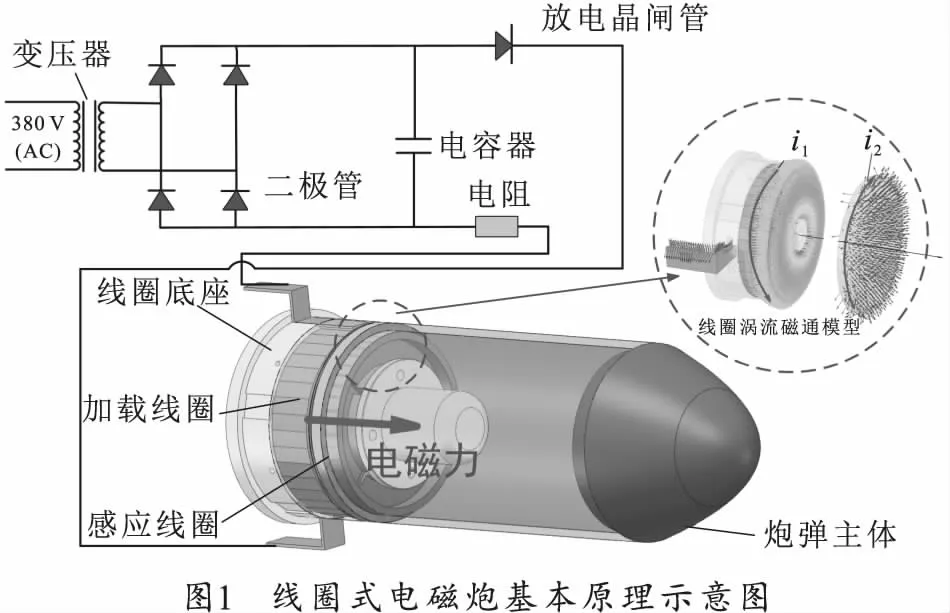
笔者研究的线圈式电磁炮的加载线圈由铜带轴向缠绕安置在线圈底座上，螺线铜带用玻璃布包裹并用环氧树脂进行匝间填充以达到铜带之间绝缘的要求。螺线铜带缠绕的线圈的几何尺寸关系如下：

r1=r0+(n-1)(a+b)，

(1)

式中：r1为铜带线圈半径；r0为铜带起始半径；n为线圈匝数；a为铜带厚度；b为匝间间隙。

放电过程中，电容产生的放电电流为i(t)，峰值为Im。将N匝的加载线圈等效为单匝圆环截流线圈，则等效为单匝的加载线圈放电电流i1(t)为

i1(t)=Ni(t)=NIme-δtsinωt.

(2)

感应线圈为炮弹的尾端底板或在炮弹与加载线圈间放置的导磁金属板，将其等效为单匝圆环截流线圈，等效涡流i2(t)与等效放电电流i1(t)方向相反。据相关文献研究[15]，可求出等效涡流i2(t)：

i2(t)=ANIme-δtsin(ωt+φ)，

(3)

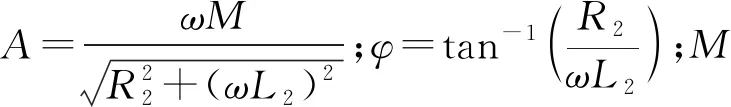
参考文献[16]推导感应线圈所受斥力为

(4)

式中：α为加载线圈与感应线圈的间距。进一步，可以得到系统的电磁发射力为

(5)

基于上述原理研制了一种多应用场景线圈式电磁炮，如图2所示，其主要由发射系统、控制系统和瞄准系统组成，发射系统为炮体的主要结构，用于安放加载线圈实现对炮弹的电磁加载，同时在平行炮筒轴线上安放红外激光瞄准系统；控制系统用于对储能电容充电后对加载线圈输出大脉冲电流，控制系统主体安装在电气柜中。

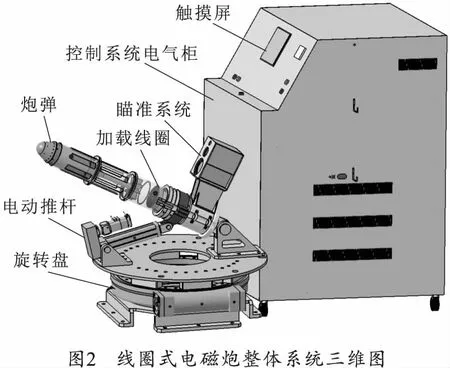
1.2 线圈式电磁炮控制系统

线圈式电磁炮控制系统主要包括充放电电路模块、触发电路模块和控制模块三大模块，其中充放电电路模块主要用于实现将电能存储在电容中，并将其转化为电磁能；触发模块用于输出触发脉冲，实现对特定元器件的通断控制；控制模块主要由PLC、触摸屏以及相应的电路模块和传感器组成，通过触摸屏的操作完成电磁炮的发射过程。

控制系统的硬件部分布置在电气柜中，并出于抗电磁干扰的目的采用物理隔离法将核心元件和干扰源分离。各电路模块的布置及电气柜实物如图3所示。

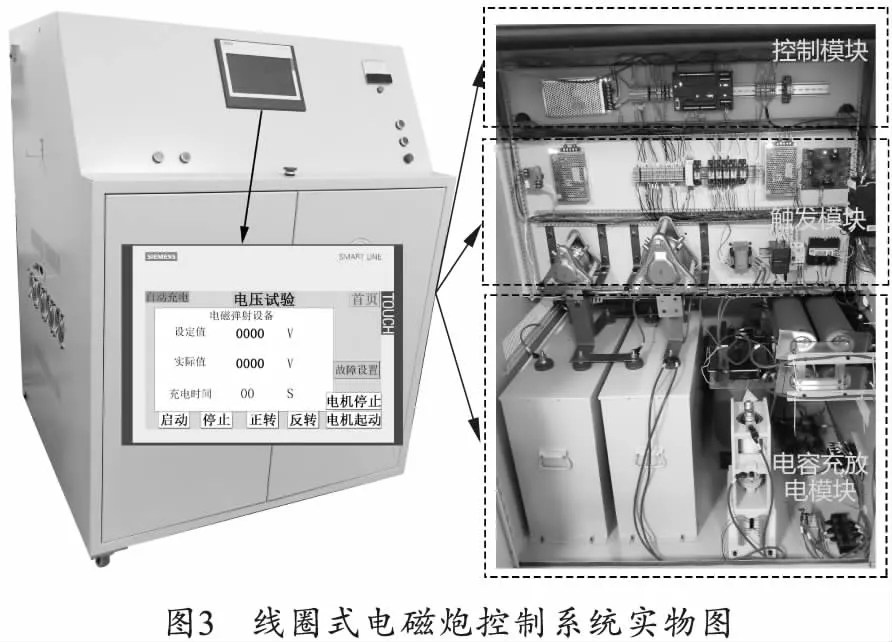
充放电模块的放电模块包含两个回路，如图4所示，第1个回路为加载线圈放电回路，由储能电容C、续流二极管D和晶闸管SCR3组成。当电容完成充电后，晶闸管SCR3导通，产生大脉冲电流对加载线圈Coil放电，当放电回路中脉冲电流减小时，加载线圈产生的感应电动势经续流二极管D继续形成回路，避免对电容的反向充电。第2个回路为泄流回路，由电容C、真空接触器K和泄流电阻R2组成，若放电回路中出现故障时，可以通过接通真空接触器将能量泄流，起到保护作用。

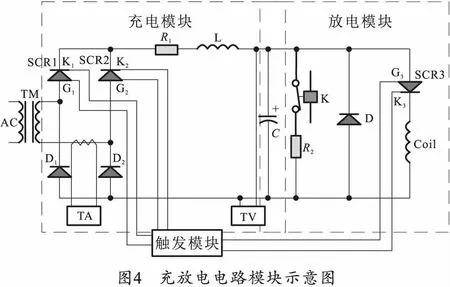
在加载线圈的放电回路中，运用了RLC回路的暂态特性[17]。图5(a)中L1、L2分别为加载线圈回路和感应线圈回路的电感，因为感应线圈只影响放电回路的互感，所以可以将放电回路简化成图5(b)所示等效电路。R为回路总电阻，包括电缆线电阻和加载线圈电阻；L为回路总电感，包括电容电感，电缆线电感以及线圈的自感和互感。

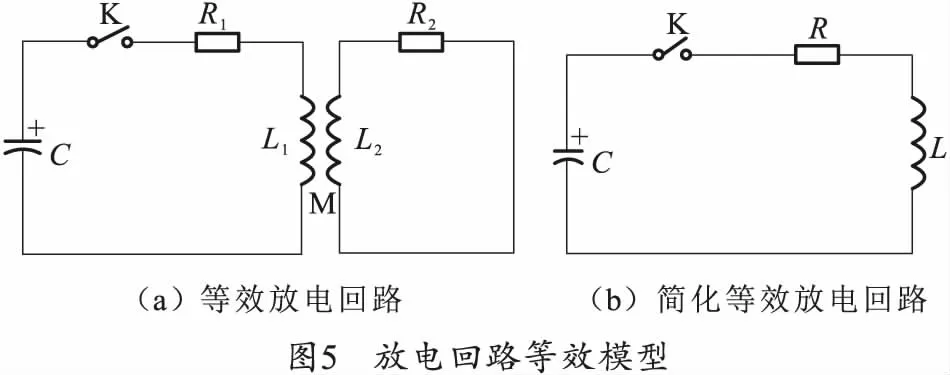
由基尔霍夫定律可得，在放电过程中放电电流满足微分方程：

LCi″+RCi′+i=0.

(6)

对于上述二阶常系数线性微分方程，满足初始条件：

i(0+)=i(0-)=0，

(7)

uc(0+)=uc(0-)=Ec，

(8)

式中，Ec为电容电动势。

由式(6)得到放电回路微分方程判别式：

Δ=R2C2-4LC.

(9)

(10)

(11)

当放电回路处于欠阻尼振荡状态时，放电时回路电流迅速上升达到峰值后下降形成反向电流，电流降至反向峰值后继续回升，如此反复振荡直至电流衰减为0。其中振荡周期T为

(12)

2 关键电路参数建模

2.1 线圈式电磁炮发射过程耦合模型

笔者借助ANSYS Maxwell的3D瞬态求解器，建立了线圈式电磁炮发射过程加载线圈和感应线圈的实体模型，其中加载线圈半径r1为62.5 mm，螺线铜带起始半径r0为7.5 mm，铜带厚度a为2 mm，匝间间隙b为0.5 mm，匝数为23匝。为了节省计算成本，感应线圈及炮弹的运动域长350 mm，满足炮弹加速至峰值速度时所需的位移。需要注意开放式的加载线圈的伸出端必须与计算域重合。运动域及计算域都为空气环境，默认发射炮弹的质量为3 kg。

为了提高计算精度，需要对模型的网格划分和分析步设置进行优化。加载线圈通过瞬时电流会导致炮弹底板的感应线圈磁通变化并产生感应电动势形成涡流，由于集肤效应，电流总是朝向炮弹底部的感应线圈表面集中。感应涡流在一个集肤深度内会衰减60%～70%，所以感应线圈厚度至少为2倍的集肤深度，在一个集肤深度内至少保证划分2层的网格。在进行Maxwell仿真分析时，对电磁炮线圈采用外部电路添加激励的形式，将图中放电模块等效为外电路赋予加载线圈，等效放电回路的各参数皆按实际测量值设置。建立电路模型时，假设放电回路的等效电阻是线性元件，忽略由于集肤效应导致电阻阻值随频率变化的情形。外部电路如图6所示。

2.2 运动域设置对仿真结果的影响

在Maxwell建立仿真模型时，需要对感应线圈设置运动域，一方面可获得炮弹发射的速度和位移的计算结果，更重要的是，若不施加运动域，则软件在计算过程中假设两线圈之间的电磁斥力不会导致感应线圈运动，即两线圈之间的间距默认贴合保持不变。放电电路除电压外，其他参数如6图设置保持不变，模型中设置了运动域和没有设置运动域，得到了在1 kV和2 kV放电电压下的电磁力模拟结果，如图7所示。

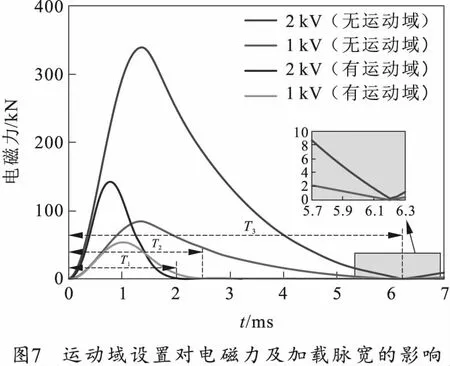
当不设置运动域时，1 kV和2 kV电压下，电磁力的加载脉宽是相同的，都为T3，这符合式(5)中电压改变不影响加载脉宽的结论；设置运动域后，相同电压时，有运动域的计算结果电磁力峰值和加载脉宽都大幅小于无运动域的情况，产生这种情况的主要原因在于：随着感应线圈受到斥力推动线圈发射，加载线圈和感应线圈的间距不断增加导致电磁力的峰值和持续的脉宽都会衰减。

图8给出了2 kV电压下，随着加载线圈与感应线圈间距加大，线圈间电磁力峰值的变化以及到达峰值所需时间的变化。线圈间距越大，产生的电磁力峰值越小，同时，达到峰值耗费的时间越长。

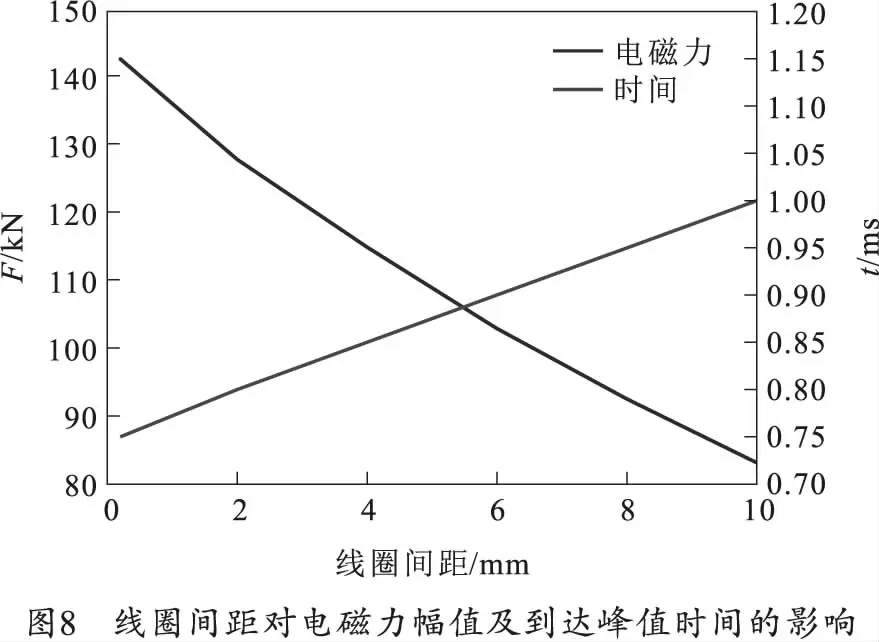
为了提高电磁炮的发射能力，应尽可能的将加载线圈和感应线圈贴合。在实际发射时，炮弹在短时间运动位移较大，线圈间产生的电磁发射力衰减较快，使得炮弹无法获得理想情况下峰值电磁力(即无运动域时电磁力曲线的峰值)的加载。所以，提高线圈式电磁炮能量转化效率应该尽可能提高炮弹获得电磁加载力对其的冲量，同时，在后续的仿真计算中，为了符合实际发射过程以及提高仿真结果可靠性，必须对模型添加运动域。

2.3 放电电压和储能电容对电磁发射力的影响

控制系统中的各电器元件特别是构成充、放电电路模块的各电路参数，如储能电容的电容量、储能电容两端的电压、放电回路的电阻值和电感值以及将炮弹低部等效成感应线圈的厚度等参数，都对线圈式电磁炮的发射能力有不同程度的影响。但在实际的应用阶段，当控制系统的硬件搭建、接线完成后，控制系统的电路参数基本固定，为了实现对不同目标的打击，使电磁炮具备可调的电磁发射能力，一般通过调节电容的充、放电电压大小和电容值的变化来产生不同的电磁发射力。

放电回路单次放电能量为

Ec=(1/2)ηCU2，

(13)

式中，η为能量转化效率。分析可知，增加电容器的容量可以提高电容器的电荷存储量，提高电容器的充电电压也可以提高电容器的电荷存储密度。

仿真计算时，放电回路其他参数如图6所示保持不变，放电电压和储能电容对发射能力的影响分别如图9、10所示。

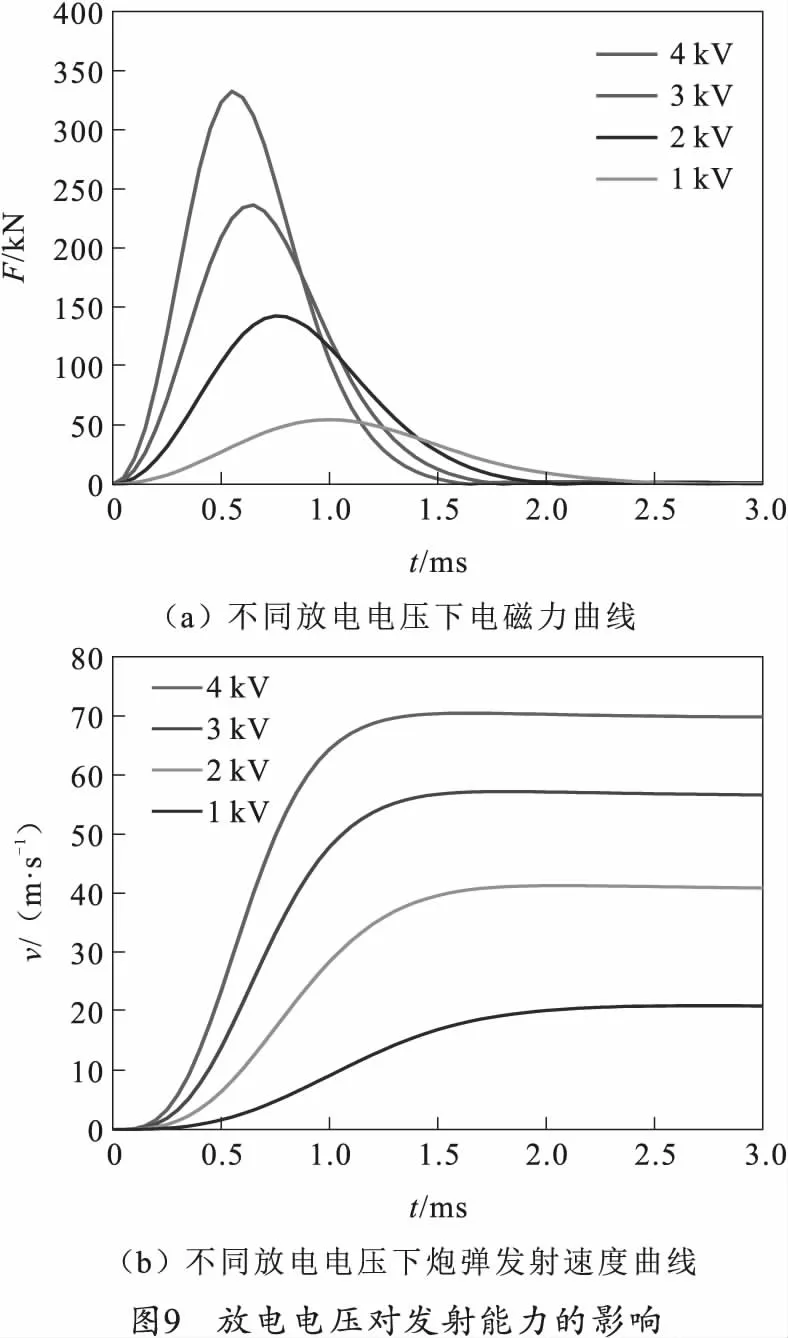
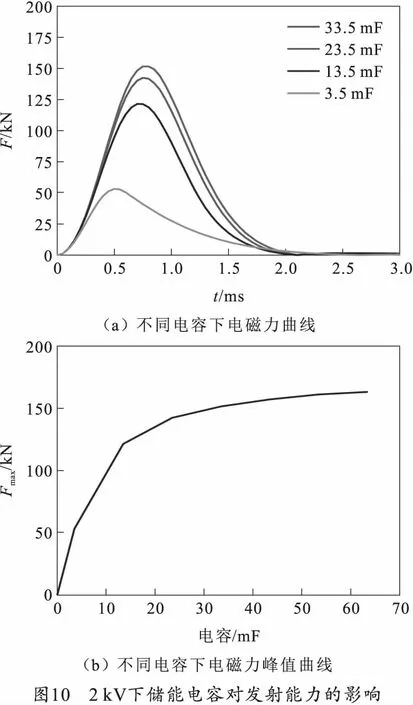
图9(a)展示了不同放电电压在线圈间产生的电磁力，随着放电电压的增加，线圈间的电磁力幅值也随之增大，但电磁力脉宽会因为线圈间距的增大而减小。如图9(b)所示，炮弹获得的发射初速也随电压的增加而增加，当前发射系统在4 kV电压下可以将3 kg的炮弹加速至70 m/s。图10中为放电电压在2 kV时，不同电容对电磁力的影响。从图10(a)中可以看出，随着电容值的增加，电磁力也有所提高，同时增加电荷存储量的释放，使得电磁力达到峰值的时间也略微有所滞后，但如图10(b)所示，随着电容量的增加，电磁力峰值的增加呈先快速上升后平缓增加的态势，所以当电容量提升至一定程度后依靠增大电容量使炮弹获取较大的发射能力的效果并不明显。

2.4 电感和加载线圈匝数对电磁发射力的影响

由式(10)和式(5)可知，放电回路中电感量变化，同时会引起电磁力幅值和脉冲宽度的变化。放电回路中电感由电容器的电感，电缆的自感、互感，加载线圈的自感、互感组成。其中电缆电感单位长度内自感一般为0.05～0.10 μH/m[18]。电缆线互感与其回路所围成的面积有关，当回路面积越大，其互感也越大。加载线圈的自感主要取决于线圈匝数与外形尺寸；互感与线圈材料、几何尺寸和与之轴向间距有关。忽略加载线圈的螺旋性和匝间厚度，并认为电流沿线圈截面均匀分布，可将其等效为空心圆柱线圈[19]。按文献[20]提供的能量法或磁链法可求得电感的解析表达式：

(14)

式中，T(p,q)关于第一类贝塞尔函数的泛函。在加载线圈和次级线圈已经确定的情况下，线圈部分的电感量也已确定。除回路等效电感外，电路其他参数如图6所示，不同电感下电磁力曲线如图11所示。可以从图11中看出放电回路电感越小，电磁发射力幅值越大，到达电磁发射力幅值时间越短，脉冲宽度也越小。

由式(1)可知，加载线圈半径、铜带尺寸及缠绕方式等决定着在有效面积上缠绕线圈的匝数。加载线圈外径尺寸和放电回路参数如图6保持不变的情况下，放电电压2 kV时，不同加载线圈匝数对电磁发射力的影响，如图12所示。

由式(14)可以看出电感和线圈匝数平方成正比关系，匝数越多，电感越大。由图11可知，回路等效电感增大会导致电磁发射力幅值的减小，但从图12可以看出，相比于提高匝数导致加载线圈电感的增大，线圈匝数的增加对提高电磁力幅值更有帮助，但匝间间隙的降低容易造成线圈被击穿。

2.5 电阻和线圈温度对电磁发射力的影响

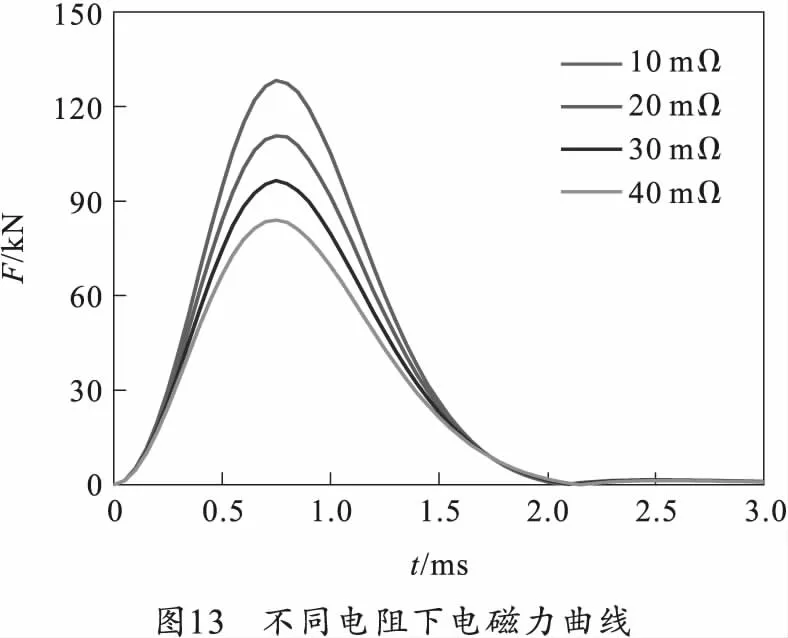
回路的等效电阻主要包括电缆线电阻和线圈电阻，保持放电回路中除电阻外的其他参数如图6不变，在2 kV放电电压时，改变放电回路电阻值的大小，其电磁力曲线如图13所示。从图13中可以明显看出，放电回路电阻越大，电磁发射力幅值越小，但脉宽持续的时间基本保持一致。

在对求解模型添加外部激励时，假设放电回路的等效电阻是线性元件，但实际工作过程中，电阻会随着电压和电流的改变而有细微的变化，此外，加载线圈工作过程中，频繁放电会在铜带线圈中积累大量的热量，也会导致回路电阻的增大。加载线圈中的热量若无法及时散出，就会对线圈的工作寿命和线圈间电磁斥力的大小产生较大影响。图14给出了实际发射环境下，加载线圈在1 kV放电电压下、间隔1 min连续工作24次的温度变化曲线。

从图14中可以看出，线圈温度在该电压下上升较快，完成24次放电温度峰值达到73.3℃后，加载线圈自然冷却。在加载线圈无外界冷却措施的情况下，线圈在经过100 min后仍无法恢复室温，温度维持在30℃左右。

实际使用中发现，加载线圈温度的上升会造成电磁发射力的明显下降。Z.Peter通过试验发现[21]，当线圈温度升高到100℃时，线圈产生的电磁力较常温时下降了15%。从能量的角度考虑，放电回路单次放电电容器产生的总的能量Ec可按式(13)计算，其中总的能量Ec转化为了耗散的热能Q和炮弹的动能EV，即

Ec=Q+EV.

(15)

由于放电回路不是一个纯电阻电路，所以不能利用欧姆定律计算电路的耗散。对任何电路而言，有

(16)

3 试验与结果对比分析

为了验证所设计的线圈式电磁炮的发射能力以及模拟结果的可靠性，利用高速相机拍摄炮弹发射过程，进而获得炮弹的发射速度。相机选取中科大千眼狼X213型超高速相机，在1 280×1 024满幅视野下的采集速度可达13 400帧/秒，实际测试时采样点的间隔时间为2.5 ms。发射过程拍摄结束后，通过高速视频目标跟踪测量软件对发射过程做后期分析，认为炮弹在相机拍摄视野做二维平面运动，忽略垂直于相机拍摄视野炮弹微小的位移分量，通过对炮弹采样时间之间位移的分析，求解出炮弹离开炮筒时的发射速度。

在实际试验中，将线圈式电磁炮固定在普通卡车上，如图15所示，采用图3所示的控制系统电源柜，电路中各关键参数值测量后如图6所示，改变炮弹中装药的质量分别为3.0、3.5和4.0 kg，测试不同质量炮弹在放电电压为1.00、1.50和1.95 kV时发射的实际速度，并与模拟速度进行对比如表1所示。

表1 不同质量炮弹在不同电压下发射速度模拟值与实测值对比

从表1中可以看出，提升电压可明显的提高炮弹的发射速度。通过笔者所述的线圈式电磁炮，在1.95 kV的放电电压下，具备将4.0 kg的炮弹加速超过30 m/s的发射能力，而炮弹为3.0 kg时，可获得36.27 m/s的发射速度。对比模拟得到的速度，实测值与模拟值的误差在9.41%～15.08%之间，相对误差基本可以控制在15%以下，且模拟速度全部大于实测的速度。在Maxwell中建立的发射模型，虽然考虑了空气阻力对炮弹发射速度的影响，但实际发射的外部环境较为复杂，且炮弹运动过程中，随着风速的改变及炮弹速度的变化，每一时刻受到的空气阻力是不同的，这是产生误差的原因之一。此外，模型中得到的模拟速度是炮弹最初发射时在炮筒能线圈附近获得的最大发射速度，但实际测量时，高速相机只能在炮弹离开炮筒后才能对炮弹进行捕捉测量，这也是造成实测值比模拟值偏低的原因。高速相机测量初速由于相机的精度限制也存在一定的误差，但总体来看，15%以内的误差在实际测试过程中可以接受，也验证了仿真模型建立的可靠性和所得结论的准确性。

4 结论

笔者研制了一种线圈式电磁炮，从电磁加载原理出发设计了一种放电电路，用于实现对加载线圈提供大脉冲的放电电流进而产生电磁力将炮弹发射。同时，通过仿真模拟进一步对影响发射能力的因素进行了分析，并通过试验对分析结果进行了验证。所得结论如下：

1)Maxwell 3D瞬态求解器中设置运动域对炮弹发射过程的仿真结果的准确性至关重要，若不设置运动域，会默认加载线圈和感应线圈间距不发生改变。

2)提高放电电压和电容可获得更大的电磁力和炮弹的发射速度，电压的增加可以显著提高电磁力幅值并缩短幅值到达的时间，而电容量增加到一定程度后，对电磁力峰值的提升并不明显。

3)加载线圈匝数越多电感越大，电感的增大不利于电磁力的增加，但增加匝数对提升电磁力幅值的影响超过随之增加的电感导致电磁力幅值降低的影响。

4)电阻的增加会导致电磁力的降低，同时，温度的上升也会导致能量转化效率的降低。

5)借助高速相机获得了3种不同质量的炮弹在3种放电电压下的发射速度，将实测值与模拟值对比，由于模拟值无法考虑实际发射的外部环境，且和实测值存在炮筒长度的位移误差，故模拟值全部比实测值偏大，但相对误差基本在15%以内，证明模拟结果具有一定的价值。