基于鲸鱼算法的供应链多解耦点决策模型
胡雪芹 韩梦玮
(中国人民大学商学院,北京 100872)
引 言
近年来,全球市场细分急剧增加,产品也逐渐趋于个性化或定制化,特别是电子产品售后服务行业,由于品牌和电子产品的快速迭代,不同国家的客户需求特点也差异巨大,这些要求企业必须重新思考或重塑他们的售后供应链,以生存并获得竞争优势[1,2]。在这一背景下,要求企业具有很高的灵活性,也需要极强的适应能力和响应能力[3,4]。研究表明,当今的电子产品有着生命周期缩短、新的生产技术更迭快速的特点,而消费者在购买差异化产品的同时首要考虑产品的性价比。电子产品售后供应链企业既需要提供个性化的服务,同时还要控制生产经营成本,因此精敏供应链是解决这一问题的重要途径[5-7]。精益策略更适合需求可预测、品种较少、产品生命周期较长的市场[8,9],而敏捷策略最适合需求波动较大、品种较多、产品生命周期较短的市场。精益策略侧重于最小化浪费,而敏捷策略则更侧重于解决不断变化的客户需求,这种精敏策略既可以满足不同国家地区对售后服务需求的巨大差异,同时还能够帮助售后服务企业降低成本[9-12]。
以往研究采用客户订单解耦点(CODP)来区分供应链中的精益和敏捷操作[13]。在CODP上游使用精益和基于预测的推动方式进行生产,而在CODP下游注重敏捷性和按客户订单的拉动生产方式,以达到供应链各环节尽可能灵活[14,15],CODP将客户驱动与预测驱动的生产和服务区分开来[16]。在塑造精敏的售后供应链中,既需要考虑产品又需要考虑服务,原因在于电子产品在全球的售后服务很大程度上是采用整包管理,其中包括售后备件供应链管理、海外备件售后维修系统 (CRM)、售后服务管理以及当地服务商管理(ASP)等部分,因此全球售后服务也同时变成了 “产品+服务”的竞争模式[17-22]。在产品服务供应链中,如何确定客户订单解耦点CODP是售后供应链整包商需要考虑的,高的服务水平能够提高客户的满意度,高的生产能力以及产品需求能够提高运营效率,但是高服务水平意味着高成本,高生产能力意味着产能过剩、库存成本增加的风险,此外全球整包售后服务会面临服务品牌产品多样化、不同国家的客户订单差异化较大等特点,因此为分散的多样化订单提供个性化产品和服务是需要迫切解决的。
精敏供应链设计的重要性越来越大,但在精敏供应链的设计过程中,存在着严峻的挑战。精益生产的主要研究包括推拉供应链、延迟生产、大规模定制等方面,而其中最为重要的是寻找客户订单解耦点CODP的具体位置。CODP可以位于供应链的不同位置,CODP上库存以通用 (或半成品)形式存储,以确保产品定制更大的灵活性[23,24]。这种供应链设计的有效性最成功的例子是惠普 Deskjet-Plus供应链[25],而不少企业都通过使用精益生产的推拉策略取得了显著的实践成果[26]。也有大量的文献讨论了延迟/推拉等精敏策略的应用,主要包括生产制造行业以及服务外包行业。对于生产制造业的研究,Cochran和Kim[23]、Cochran和Kaylani[27]通过在串行生产线上建立水平集成的推拉混合生产系统 (HIHPS)的优化模型,将推拉控制应用于生产系统,并证明推拉系统优于全推和全拉系统。对于服务外包行业,研究了众多物流企业协同整合,形成服务供应链以满足客户的个性化服务需求,Wang等[28]通过分析订单解耦点CODP的具体位置来最大限度的提供大规模服务的能力,Liu等[14]研究了服务集成商通过分析新订单的插入问题来判断订单是否被接收。对于CODP的研究方法上,主要是权衡供应链绩效的关键指标——库存成本和服务成本之间的关系,精益供应链(推式供应链)偏重于服务成本,而敏捷供应链(拉动式供应链)偏重于生产库存成本。Olhager[29]通过在不同地点设置需求满足点,提供了4种不同的推拉式供应链设计策略,并构建了一个基于产品交货期比和相对需求波动率的决策模型。此外,Salum和Araz[30]通过比较双资源约束/推拉控制系统和双资源约束/看板系统,展示了推拉控制在生产系统中的应用。然而以往研究都是基于最终客户的拉动,而实际情况为解耦点之后到最终客户之前的节点依然会产生补货需求,而这种连续补货需求在以往研究中并没有被考虑,因此本文和其他研究的关键区别在于本文基于连续补货情况下分析了精敏供应链CODP的位置。
而随着成本的增加、时间的不确定性、利润率压力、全球化、模块化、复杂性和竞争、需求品种、需求的多样性,识别供应链中单一的战略解耦点越来越困难,而这种不确定的生产服务供应链环境,需要在具有多个解耦点的定制制造系统中建立一个更好的CODP调整模型和策略[31]。由于当今商业的全球性,研究人员强调需要考虑全球产品价值链,而不仅仅是单一实体链[31-34]。这种困难主要是由于在全球供应链网络中需要灵活、反应灵敏的精益和敏捷的产品供应系统。多个解耦点的确定将整个产品价值链分解为多个精益和敏捷系统。精益系统创建跨实体的拉动机制,敏捷系统帮助每个实体保持灵活性和响应能力[31]。Chung和Ng[35]提出了电子产品价值链中基于形式、时间和地点3种延迟的多重解耦点。该研究强调需要查看整个产品链,以确定在价值链的各个层次的解耦点。Sun等[36]讨论了基于MTO-MTS交互作用的材料清单中多个解耦点的识别和定位,以及如何有效地将它们用于最低制造成本。随着数字时代的不断发展,3D打印、RFID、大数据分析等技术的发展,将提升供应链的整体效率,同时将带来售后整包供应链解耦点CODP的变化,这在以往研究中是没有被提到的。
和以往研究不同,本文创新性的引入优化鲸鱼算法(Whale Optimization Algorithm,WOA)求解CODP。WOA是2016年提出的一种新的群体智能(Swarm Intelligence,SI)算法,它模拟座头鲸在围捕猎物过程中典型的气泡网攻击行为来解决优化问题。与其他优化算法相比,WOA具有过程简单,收敛速度快,所需调整参数少,主动搜索能力强等优点。因此,WOA在许多领域得到了广泛的应用。Alameer等[37]提出使用WOA训练神经网络来解决非线性回归问题。Harikarthik等[38]使用人工神经网络分类算法和WOA来检验软件错误。Guo等[39]提出了一种基于社会学习和小波变异策略的WOA,并将其应用于解决水资源的3个预测模型。Wang等[40]提出了一种基于WOA的新型混合系统,它包括4个模块:数据预处理模块、优化模块、预测模块和评估模块。由于WOA具有的快速收敛、精度高的特点,WOA被广泛应用于解决工程问题等[41-44]。WOA 有着极大的研究价值和应用价值,而目前缺少WOA在物流与供应链领域解决CODP问题的研究。
因此本文针对售后整包行业的精敏供应链的决策问题,构建连续补货的多解耦点决策模型,应用WOA分析不同解耦点策略的选择对供应链库存成本和服务成本的影响,并阐述订单折扣率、惩罚率,技术投入等因素对最终成本的影响。
1 问题与基本性质
在现实交易活动中,售后外包的产品和服务需求可能无法从终端产品库存中获得,这将引发其他从终端库存不断的向上游中间产品库存下单补货,且客户需求订单和下游补货订单可以同时到达系统的多个阶段,这就形成了多个链式反应复杂模型。不同的客户需求订单应该采用多解耦点的方式进行分析,而不同解耦点的位置选择将会带来不同的订单延迟情况。本文通过描述订单延迟度和总成本之间的关系来确定解耦点的位置,成本主要包括库存及生产成本、服务成本以及技术投入成本等。对于库存及生产成本主要受到客户需求的订单量、提前期、补货率、零部件再利用率等因素影响,服务成本受到未能满足客户交货期DLT的违约成本以及延长客户交货期的订单谈判折扣成本的影响,而技术投入成本主要是指现代信息系统或采用复杂的通信技术而产生的成本。
本文假设供需过程是由若干个供应阶段以及不同需求提前期的客户组成。对于供应端,假设供应链有N个阶段,1是起始阶段,而N是终点阶段,每一个阶段都可能会形成一个库存点。即SP(i),i=1,2,…,N。用SP(PB)表示供应链的解耦点,具体而言,这代表SP(1),SP(2)至SP(PB-1)是采用推式生产,在SP(PB)之前各加工环节采用预测生产标准件,为了简化计算,本文假设SP(PB)之前各加工环节都不是存放库存,而SP(PB)是第一个库存点(即解耦点),在SP(PB)之前各加工环节的标准件全部送到SP(PB)进行储存,这些加工环节并不保留任何中间库存。而SP(PB+1)、SP(PB+2),至SP(N)将成为后续的可能解耦点,这些点都会有库存,实际订单触发这些库存点,且随着N逐渐增加订单的延迟程度逐渐变小。
对于客户端,客户订单假设为一个到达速率为λ的泊松过程,每个客户只订购1件,客户采用提前订货。对于传统的订货订单,客户往往是在到达维修点后才提交订单,供应商告知客户从下单到获得商品的等待时间(客户订单完成的提前期)是w1;而对于数字化系统的应用,这一策略带来了预先需求信息(Advance Demand Information,ADI)采集,根据预购策略,商家提供数字化平台鼓励客户在实际需要之前φ时间单位下订单,因此其实际等待时间变为w2(w2<w1),φ为承诺提前期(客户根据价格不同而自己进行的提前选择)且是连续变量,客户往往会根据传统订单的等待时间来估计承诺提前期的长度,因此客户会将φ设置成w1(即φ=w1),此外供应商会提供一定的补偿,客户每延长提前期1个单位,商品(服务)价格降低K单位,因此可以表示为K(φ),本文假设K(0)=0,且K(φ)在φ的承诺提前时间长度上是严格递增且凹的,承诺成本的凹凸性目的是使得更长的承诺交付时间对客户更有吸引力。客户的平均等待时间应该小于或等于最大等待阈值ω。设顾客等待时间为W(Ii,φ),其是由被分配到的具体节点位置的基准库存值Ii和承诺提前期φ决定的,因此顾客的平均等待时间是(Ii,φ),并且FW(Ii,φ)(ω)=P{W(Ii,φ)≤ω}是顾客实际等待时间的累积分布函数,对于传统供应链而言φ=0,对于数字化供应链而言φ≠0。
对于供应端,由于供应商在接收到客户订单后,会根据客户预计的等待时间(w1或w2)的不同确定客户的提前期DLT,对于传统供应链而言,其客户的提前期为w1,而对于数字化平台的供应链而言,其客户提前期为w2+φ,且根据前文分析可得w2+φ≥w1。供应商将提前期不同的订单安排在不同的供应链节点上,以确保客户订单能够完成,而每个位置的库存点都有能够服务的客户订单提前期的时间范围。设ti(α)是距离库存点SP(i)的安全剩余交货时间,它是从sp(i)(中间产品库存点)开始到货物可以向客户交货的时间估计。假设第i个阶段的补货提前期都有一个概率分布,且假设其符合正态分布。然后SP(i)的剩余提前期(从SP(i)的半成品被取走到成为成品并准备好供客户取走的时间)被定义为SP(i)后所有剩余提前期的卷积分布。设hi(x)是SP(i)剩余提前时间的概率密度函数,公式如下。
hi(x)=fRi+1(x)×fRi+2(x)×…×fRN-1(x)×fRN(x)
那么SP(i)的安全剩余交货时间ti(α)为SP(i)的剩余前置时间分布的α分位数,公式如下,其中Hi(α)是hi(x)的累积分布函数。

一旦确定了所有库存点的安全剩余交货时间,就可以计算客户订单在SP(i)时完成的百分率。假设存在来自所有客户交货期可能值的概率分布fDLT(x),可以根据ti(α)获得所有库存点上客户订单完成的百分比,FDLT(x)是fDLT(x)的累积分布。p(i)是最终的供应商将订单分配到SP(i)库存点的客户订单百分比。
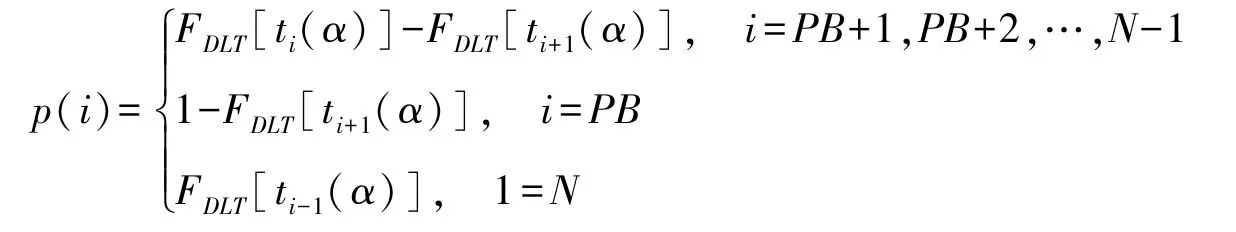
具体而言,如果订单交货期比tN-1(α)小,那么供应商则需要将订单安排在SP(N),而在SP(N)完成订单的概率是Pr[DLT<tn-1(α)] =FDLT[tn-1(α)]。
根据以上分析可得,α在[0,1]之间,当α趋于0时,供应链整体设定的生产和补货时间应该更短,则ti(α)减小,这意味着供货企业设定的安全剩余交货时间比较小,节点更愿意为落在DLT 0-ti(α)范围内的客户提供服务,供应商设定的节点的安全剩余交货期(时间底线)更严格,DLT时间更长的客户只能被安排在更上游的地方(i-1节点),也就是供应商将按订单定制节点i放到更靠近客户的地方,专门满足那些订单时间要求更紧迫的客户,此时客户的库存成本更高,但是客户响应速度快,服务成本较低;相反,如果当α趋于1时,供应商在节点i几乎愿意满足全部的客户需求,供货企业设定的安全剩余交货时间比较长,则ti(α)增加,这意味着供货企业设定的安全剩余交货时间(时间底线)更长,节点i则愿意为DLT更大的客户服务,DLT时间更短的客户只能被安排在更下游的地方(i+1节点)才能保证客户的要求,此时库存成本比较低,订单响应比较慢,可能导致服务成本高。此外,如果α的值比较高,那么此时被分配到上游库存点的订单比较少,大部分订单获得了较好的服务;如果α的值比较低,那么大部分订单被分配给了各上游库存点,此时整个供应链的总库存值较低。因此供应商通过控制α的值,来对ti(α)(剩余安全交货时间)进行决策,进而控制不同的成本状况。另外,对于供应商而言,如果只有1个解耦点,那么ti(α)将客户订单分成两类,一类是客户订单提前期大于ti(α);另一类是小于ti(α),而本文采用多个解耦点的做法,不同类型的客户有不同的提前期要求,因此也就意味着将有多个ti(α),那么客户提前期将会划分成多类。DLT是客户的交付期限,本文参考 Sinclair[26]、Humair和 Willems[45,46]的研究,设置 DLT 和ti(α)的关系来判断订单应该安排在哪个阶段。如果DLT<t(n-1)(α),那么订单应该发往库存点SP(N),如果t(n-1)(α)<DLT<t(n-2)(α),那么订单应该发往库存点SP(N-1)。本文主要参数设置如表1所示,过程相关参数如表2所示。

表1 主要参数设置

续 表

表2 过程相关参数

续 表
综上所述,解耦点位置的选择不仅会影响供应商库存成本和服务成本,还会影响客户获得商品的时间满意程度,因此本文针对带有补货过程和客户预先需求信息采集的供应链订单解耦点问题进行研究。
2 传统供应链解耦点模型
对于传统供应链而言,并没有数字化平台可以提供客户信息的提前采集,往往是通过客户到达商家后,了解商品能够提供的时间,进而被动的确定提前期,因此对于供应商而言,利润函数=销售收入-库存持有成本-服务延迟成本-与顾客协商折扣成本。具体如下所示:

该函数的第一项销售收入,在提前期内的需求量乘以销售价格,其中销售价格是固定值,不随提前期的变化而变化,第二项是库存成本持有成本,即h(持有成本率)乘以解耦点和所有拉点处的预期库存价值之和,因此单位库存保持成本是非线性的,因为随着库存越靠近下游,vk值越大,持有成本也相应越大;第三项是服务延误成本,单位延迟成本被定义为产成品价值成本的一部分,因此是vi的线性函数;第四项是预期折扣成本,最后客户的付款期限非常短可能会导致无法按时交货而必须付出的折扣成本,供应商提出的折扣是为了吸引tn(α)比DLT更长的客户。另外,由于PB(解耦点)的位置不同,会导致不同的N,因此对于供应商而言,应该求得利润最大值时的解耦点位置。如果只设置1个解耦点,那么i就是PB,则只有p(i)>0,其他节点直接安排订单需求的概率为0,意味着在其他点不进行分配,如果存在1个以上解耦点,那么就需要单独计算不同p(i)的值。
接下来,进一步求得公式中的第一项库存持有成本。(1)计算直接被安排在SP(i)库存点的需求订单量;(2)计算SP(i)的生产时间和补货时间,补货提前期显著影响模型中所有拉动点的库存水平,由于本文的优化模型是一个多阶段联动的随机服务模型,因此刻画随机补货提前期是一个关键挑战;(3)推导出包含补货订单的平均库存值;(4)根据直接安排到该节点的订单数,确定该节点的实际库存情况;(5)根据前面计算结果,求解E[Ii()]。因此在每个拉动点,有两种类型的订单:特定的客户订单和来自连续拉动点的补货订单。本文根据周期盘点库存且库存补充到库存基准值(Base-stock Level)Si的时刻则停止补货,因此库存点i的库存=S-被分配到节点i处的订单数Di(0,DLT),具体分析过程如下所示:
SP(i)节点每审核周期的平均生产要求是ui,该节点第一个单元的生产时间是zi,剩余单元的生产时间是xi,那么实际总生产时间是(ui-1)+xi+zi小时,在生产过程中,每单位生产运行时间中都可能发生停机事件,那么预期停机事件为niμdi。因此总生产时间为:

方差的推导如下所示,为了简便,去掉i,用P、V、N分别代表生产时间、生产量、停机次数。通常来讲,普遍认为停机的发生被建模为泊松分布。varP的单位是小时平方。

式 (6)的得出是由于假设停机时间服从泊松分布,将式 (3)和 (6)代入式 (2)中,可得:

再将式 (7)、(8) 代入式 (1) 中,可得到vP。
而总补货时间μRj是由物料提前期+物料延迟时间+总生产时间组成,假设在每次补货的情况下,最多只延迟一种物料的投入,原因在于通常对材料的管理使得材料的可用性水平非常高,多个材料输入延迟的概率非常小。因此物料部分延迟的概率为1-Aj,物料的平均延迟时间是μmj。
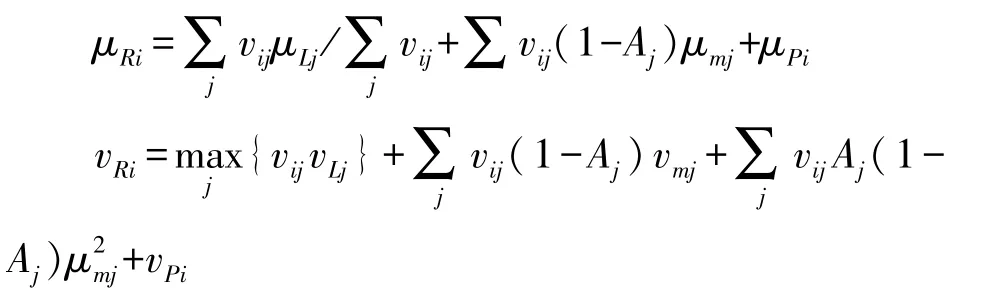
因此,本文计算在补货提前期和审查期间的预期需求μTj:

进一步,进行库存成本的推导。被安排在SP(i)的客户订单的等待时间大于审查周期的概率是相当于在μRj期间内的需求大于等于Si(商家在节点SP(i)的补货量)的概率。本文用正态分布进行估算,大于z的概率用来表示。因此,可以得到以下临界值:

因此:

在收到补货批次之前的平均库存水平是安全库存。收到一个补货批次后的平均库存水平是平均补货规模,因此,对于库存水平,本文认为每个库存节点i的库存值是固定的,原因在于安全库存水平是根据供应商自身的生产和补货水平进行的预估,且固定审核周期内的客户到达的平均值也是固定的,因此在每个审核周期中,Ii=Si。

因此由于给定特定的客户样本,其DLT分布即确定,且根据以上分析可得μRj和vRi,那么供应商根据不同α的取值,确定ti(α)的值,那么根据p(i)=Pr[ti(α)<DLT<ti-1(α)] =FDLT[ti-1(α)]-FDLT[ti(α)],可以得到不同节点处分被分配的实际客户量:
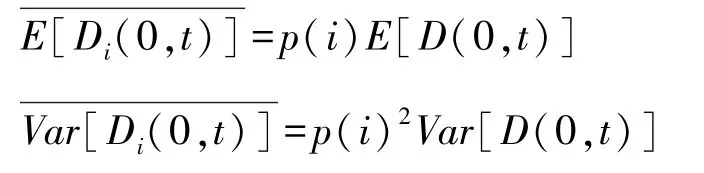
为了找出承诺提前期的有无或如何影响等待时间和长期平均总成本,需要定义以下符号:
D-(t1,t2]: 从t1到t2的累计客户订单,t1<t2。
D(t1,t2]: 从t1到t2的累计客户需求,t1<t2。
IO(t):t时刻未完成订单数量。
IN(t):公司在t时刻的净库存水平。
IP(t):公司在t时刻的库存状态值。
对于一个传统的库存系统(即,未采用数字化平台系统采集承诺提前期),净库存水平遵循简单的流量守恒定律:

当系统在基础库存水平为Ii=Si的基础库存策略下运行时,每个客户需求触发1个补货订单,并且认为IP(t)在一段时间内具有固定行为∀t>0,IPi(t)=It,那么INi[t+ti(α)] =Ii-D(t,t+ti(α)]。
3 数字化平台系统供应链解耦点模型
对于数字化平台系统,其采用提前采集承诺提前期φ,此时的库存是基于客户订单的基准库存政策(Order-Base-Stock Policy)。根据该策略,每个客户订单都会触发1个补货订单。在基准库存水平为Ii的订单基础库存策略下,IP(t)=IN(t)+IO(t)不再是随时不变的,因此对这一库存状态进行修正,令IP-(t)=IP(t)-D(t,t+φ],修改后的库存位置取决于承诺提前期的某一时间段内已知的需求,因此IP-(t)在∀t>0,都有IP-(t)=Ii,如果IP-(0-)≤Ii,那么差值被立刻订购以保证IP-(0)=Ii,如果IP-(0-)>Ii,节点i不订购任何订单直到需求使得IP-(t)=I,一旦IP-(t)=Ii,那么将持续保持下去。

对于传统供应链而言,φ=0,而对于数字化平台的供应链而言,由于每个客户的订单在φ时间后都变成了客户的需求,因此D(t1,t2]=D-(t1-φ,t2-φ],因此IN[t+ti(α)] =Ii-D-[t,t+ti(α)-φ],其中D-[t,t,+ti(α)-φ]表示ti(α)-φ时间长度区间内的客户订单数。为了简化,本文定义IN表示IN(t),以及X(φ)表示D-[t,t+ti(α)-φ],那么IN=Ii-X(φ),则INi(t+μRi)=Ii-Di(t,t+μRi),对于传统供应链而言,由于没有提前采集客户的订单需求,因此承诺提前期φ=0,因此供应链的整体库存如下所示:

3.1 预期库存水平推导
所有SP库存点之间的相互依赖是定义整个供应链行为的关键。假设在t时刻,一个客户订单被分配给SP(N)来完成,此时的订单需要进一步向上游拉动,直到在SP(PB)停止拉动,等待时间的长短取决于SP(N)的补货提前期(RLT)。SP(N)的RLT取决于第N个生产阶段的交货提前期以及库存点SP(N-1)的等待时间(这个等待时间是由于SP(N-1)的缺货概率 1-F(N-1)引起的),这一过程一直将重复到SP(PB)。SP(PB)的等待时间只取决于前面所有生产阶段的提前期之和以及SP(PB)的补货率。因此,定义0~1变量S(i),表示在库存点SP(i)处是否发生缺货(PB<i≤N)。由于本文是基于电子产品售后整包行业,各库存点的补货率F(i)将会受到零部件的回收再利用率的影响,回收利用率越高,补货率则越高,因此本文采用ai来表示每个库存节点对于零部件的回收利用率,ai+F(i)表示回收率对于补货率的提高程度,为了表达简便,在公式推导中暂时不加入ai。

其中,TRLT(i)是SP(i)的补货提前期,TPT(i)是生产阶段i的交货期,TWT(i)是如果库存点SP(i-1)需要向上一级库存点补货时的等待时间(积压订单排队时间)。利用条件期望的性质和总方差定律,可以得到SP(i)处RLT的期望值和方差为:

然后,根据SP(i)处RLT的期望值和方差,推导出补货提前期内的预期需求。假设客户订单是独立的,那么补货提前期内需求量的期望和方差分别为:

为了计算条件期望和条件方差,本文使用Lee和Billington[47]的等待时间概率函数作为基础来描述分配给多个库存点的需求。Gi(j)是等待时间比j大的概率。


又由于Gi(0)是等待时间比0大的概率,因此Gi(0)= 1-F(i),可以求解出:

所以SP(i)处的期望库存为:

本文将通过鲸鱼算法的解空间确定决策变量F(i)和α。E[TPT(i)]和Var[TPT(i)]在本文认为是已知的变量,这个链式反应中的关键变量是E[TWT(i-1) |S(i-1)= 1]。递归链式反应是从S(PB)点开始的,由于PB是订单拉动点的边界,因此该点不存在进一步向上游补货的情况,因此此时该点只与TPT(PB)以及F(PB)相关,而这些是已知变量。然后进一步求得GPB+1(j),以及E[TPLT(PB+1)]和Var[TRLT(PB+1)],同样的过程求解SP(PB+2)。这个过程一直持续到SP(N)的计算完成为止。
3.2 预计延误成本推导
本文选择的关键指标是满足DLT的时间百分比。Γ(i)=ti(α)+τ,其中Γ(i)是目标订单在SP(i)处的可接受提前期,τ是客户对订单延迟的最大容忍时间。
预计延误成本是由每个SP在收到被分配订单的Γ(i)内完成订单的概率来定义的。在τ=0时,通过实现Γ(i),在分配给SP(i)的所有订单中,只需要最短DLT的订单能够按时完成。这意味着如果SP(i)没有缺货(不需要可能的时间延误),所有分配给SP(i)的订单都可以按时完成。由于缺货的发生取决于SP(i),以及SP(i-1,i-2,…,PB+1,PB)的补货率,因此可以定义Γ(i)是由所有库存点SP(i)的填充率的函数(i以后所有节点的加工时间之和小于被安排在i节点的等待时间)。
当PB<i<N时,有:


Hi()是从SP(i)剩下的交货时间的累积分布函数。
3.3 预计折扣成本推导
预计折扣成本是指当最后1个库存点没有成品库存时,且提前期超过客户的订货时间,而预期的交货时间谈判折扣成本总和。它以基于产品价值的折扣形式估计所需的销售努力,以吸引CLR 比tn(α)短的客户,tn(α)是最后 1个实现点的预期提前期。该部分的成本用NC表示,有预计折扣成本为:

3.4 技术投资成本以及转换成本推导
在解耦点之后的各库存点,为了提升零件的再利用率,会投入一定程度的技术手段,如3D打印、RFID等先进技术,来修复快速翻新、修复回收零部件,进而提升库存点的补货效率,因此本文设供应链的总技术投资成本为IS,公式如下所示。在投入了相应的技术后,会带来相应补货率的提升,补货率的变化为ai+F(i)。有预期总计数投资成本的期望为:。
由于供应商在海外服务众多品牌的产品,不同品牌产品之间的差异需要考虑,不同库存点、半成品的价值不同将带来不同的转换成本,而产品差异的多样化又会继续加剧这种转换成本,因此本文采用TS表示转换成本,有预期转换成本的期望为:
4 算例分析
本文假设售后整包供应链主要由3个步骤组成:产品制造、产品测试和产品配送,因此可将该电子产品制造供应链分为3个阶段:售后产品制造(BM)、售后产品测试(PM)和售后产品配送(AM),不同阶段售后产品分别存储在原材料库(RI)、半成品库(SI)和成品库(PI)中。该售后整包供应链在传统条件下,仅有单一解耦点,如图1情形 (2)、(3)所示;而在数字化平台系统供应链条件下,将出现若干个解耦点,如图1情形(4)、(5)。

图1 传统供应链及数字化平台系统供应链的解耦点情形
本文将需求波动(DV)、交货提前期(DLT)、持有成本(HC)和惩罚率(PR)4个外部因素组合创建的16个输入场景的情形进行对比。本文设置的主要参数值如表3和表4所示:

表3 主要参数值
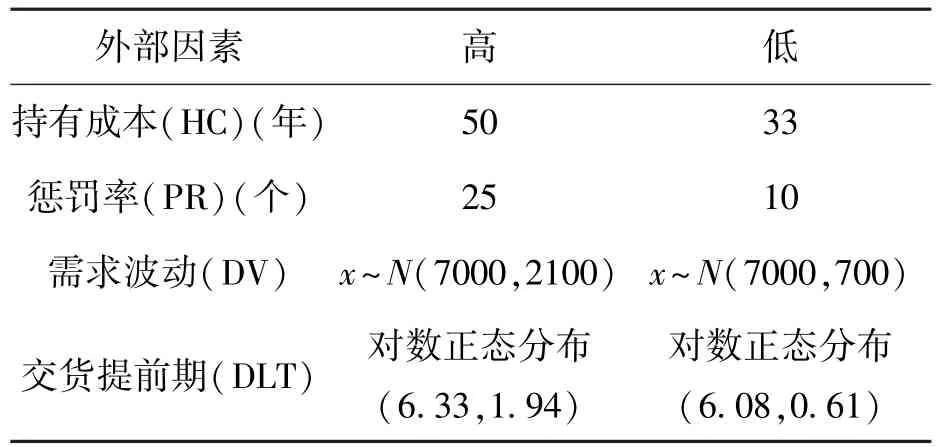
表4 高、低外部因素参数取值 单位:%
由表5输出数据可知,情形 (4)在所有情形中具有最低平均值和标准差,即此时供应链成本最低。数据分析结果表明,数字化平台系统供应链的多解耦点模式,显著优于传统供应链的单一解耦点模式。

表5 传统供应链及数字化平台系统供应链的成本
5 结束语
本文针对售后整包行业的精敏供应链的决策问题,构建连续补货的多解耦点决策模型,创新性的应用WOA分析不同解耦点策略的选择对于供应链库存成本和服务成本的影响。研究结果表明基于数字化平台系统供应链的多解耦点模式显著优于传统供应链的单一解耦点模式。
——国外课堂互动等待时间研究的现状与启示

