COB光模块耦合对准及算法研究
马铭涵,涂凯扬,段 炼,刘志贤
(中南大学 高性能复杂制造国家重点实验室 机电工程学院,长沙 410000)
0 引言
作为光电转换的连接器件,光模块一定程度上影响着光通信产业的飞速发展[1]。如今,光模块的封装种类朝着功耗更低、体积更小、速度更快的方向发展,板上芯片封装(Chip On Board,COB)技术很好的满足了这一要求[2]。COB是将光电裸芯片粘贴在PCB板上,利用较小的引线将芯片和PCB连接,因此在很大程度上提升了封装密度[3]。COB光模块的耦合对准是封装过程的重要步骤,同时也是技术难点,耦合质量的好坏直接影响到COB光模块的良品率[4]。耦合对准的目的是为了找到最佳耦合位置,从数学角度讲就是函数优化问题,解决函数优化问题一般采用数值解法和智能优化算法。数值解法中,爬山法在激光器和光纤的对准问题已经有了很多应用成果[5],但是其只能进行一维对准。2006年淳静等在解决光纤的自动对准问题时应用了模式搜索法[6~8],可以在X-Y平面两个自由度搜索,该算法经过实验证明可靠性高,不易陷入局部最优,但是仅克服X-Y两自由度的耦合误差,未沿其他自由度进行搜索。相比于数值算法,智能优化算法在求解过程中,一般不需要优化问题明确的数学表达式,因此该种算法常用于求解复杂优化问题。2012年Marc Landry等人提出粒子群智能优化算法[9],并将其应用在两根光纤间的耦合对准,该种算法简单,能够在多个自由度同时搜索,实验证明该算法可靠性高,并且不容易陷入局部最优。
粒子群智能优化算法在搜索速度上还有一定的提升空间,而自适应权重粒子群算法在很多研究中已经证明了可以通过调节权重提升搜索速度和可靠性[10]。但是其在光通信器件的耦合封装领域鲜有研究。本文分析了COB光模块的耦合对准原理,并通过实际的耦合对准实验讨论各种偏差对耦合效率的影响。基于以上分析和研究引入了自适应权重的粒子群算法并将其运用在COB光模块的耦合对准过程中,并进行了仿真和实验验证,实验结果表明该算法很大程度上提高了耦合对准效率和成功率,为COB光模块的精密封装提供了理论技术支持。
1 耦合对准
1.1 耦合对准原理
COB光模块耦合对准的原理是在光发射端将电信号转换为光信号,驱动垂直腔面发射激光器(VCSEL)发出光信号,并传输到光纤之中;在光接收端本征光电探测器(PIN)将光信号转换为电信号,实现电-光-电的转换。在此过程中,VCSEL和PIN都需要确定最佳的位置与光纤耦合,这样才能够使光信号高效传输[11]。VCSEL和PIN的裸芯片都是通过键合和贴片等工艺贴装在PCB上,VCSEL的激光发射方向和PIN的接收光信号方向都垂直于其芯片,而光纤平行于PCB板,所以和VCSEL/PIN的芯片呈90°。因此如何将光纤和芯片高效耦合是COB光模块封装的关键,本研究中采用光弯折法。如图1所示,以光发射端为例,利用反射镜使光路弯折,VCSEL发出的光经过45°的反射镜旋转90°,经过透镜射入光纤完成耦合。
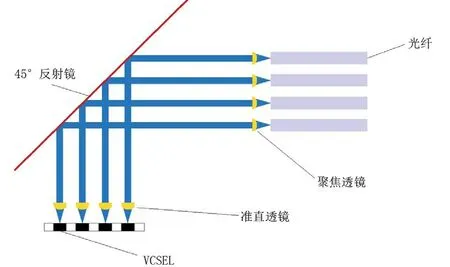
图1 光弯折法示意图
由于COB光模块四个通路间距相等,芯片和光纤互相对应,四个光路之间干扰很小,所以选用其中一路进行分析。对于光发射端和接收端,其光路如图2和图3所示。
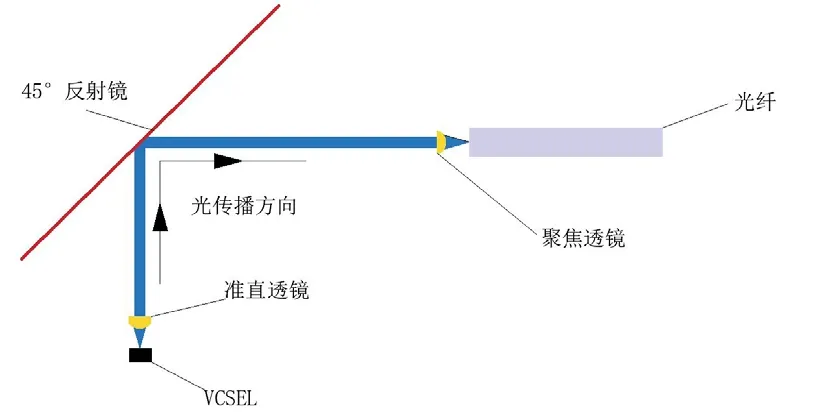
图2 光发射端光路示意图

图3 光接收端光路示意图
1.2 合对准实验
在前文对COB光模块的耦合对准原理分析的基础上,本节将进行耦合对准实验,分析不同方向偏移对和耦合效率的实际影响。
在耦合对准实验中,如图4所示,耦合时VCSEL/PIN芯片固定,反射镜、聚焦透镜、准直透镜组成Lens适配器,光纤插入Lens适配器中与之形成整体。在耦合过程中,芯片固定,因此只需考虑光纤在空间中的位置变化。实验中通过夹具控制光纤角度偏差,因此不需要考虑θx、θy、θz的偏差。X和Y方向的偏移由Lens适配器的横向位移确定,Z方向的偏移由Lens适配器的纵向位移确定。实验选取3组COB光模块对光发射端和接收端进行耦合对准,每组实验通过手动对准至耦合效率最高处,并将该点设置为偏移量为0的点,之后再进行不同方向偏移。为更好地呈现偏移对耦合效率的影响,对耦合效率采用归一化方法[12],即分母为手动耦合的最大耦合值,分子为各个点的实际耦合值。

图4 实验耦合对准示意图
光发射端和光接收端耦合对准实验数据分别如图5、图6所示。在光发射端,X/Y方向的偏移量达到±5um时,耦合效率降低到80%;偏移量达到±30um时,耦合效率接近于0;耦合效率的下降速度也较快。Z方向的偏移量达到±10um时,耦合效率为90%;当偏移量达到-80um或+100um时,耦合效率接近于0;耦合效率的下降速度较快。
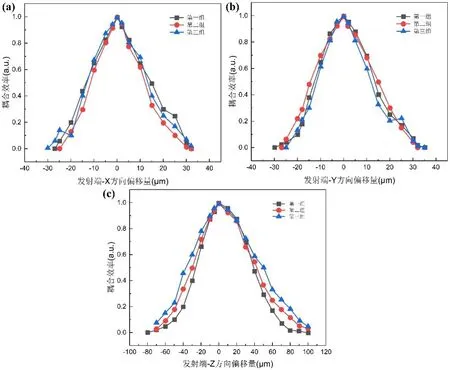
图5 光发射端耦合对准实验数据

图6 光接收端耦合对准实验数据
在光接收端,X/Y方向的偏移对耦合效率的影响与光发射端相比较小。在±5um的范围内,耦合效率无明显变化;当偏移量达到±15um时,耦合效率降至80%;当偏移量达到±50um时,耦合效率接近于0;耦合效率的下降速度相对于光发射端较缓慢。Z方向的偏移对耦合效率的影响与光发射端相比较小。在偏移量-30um至+45um范围内,耦合效率无明显变化。光接收端出现耦合效率无明显变化现象的主要原因是,与光发射端VCSEL芯片相比,光接收端PIN芯片有着更大的接收光敏面,沿X/Y/Z方向移动一定的距离,PIN芯片都能接收到光,因此在光接收端的耦合效率曲线上会出现平坦区域。当偏移量达到-60um或+70um时,耦合效率为90%;当偏移量达到-120um或+210um时,耦合效率接近于0;耦合效率的下降速度相对于光发射端较缓慢。
2 合对准算法研究
2.1 算法原理
粒子群算法(PSO)由Eberhart和Kennedy提出[13],是粒子群根据位置和适应度按照某种迭代规则进行寻优的一种算法。在求解n维最优化问题中,假设粒子群中有m个粒子,并且每个粒子都有n维位置向量和速度向量。n维位置向量表示为其代表最优化问题中的一个潜在解。n维速度向量表示为其代表粒子在迭代过程中前进的方向和距离。将位置向量xi代入最优化问题的数学模型可以得到粒子在当前位置的适应度值,记录粒子在迭代过程中每个粒子搜索到的最优位置记录粒子在迭代过程中整个粒子群搜索到的最优位置
使用式(1)和式(2)对粒子的位置和速度迭代寻优[14]:
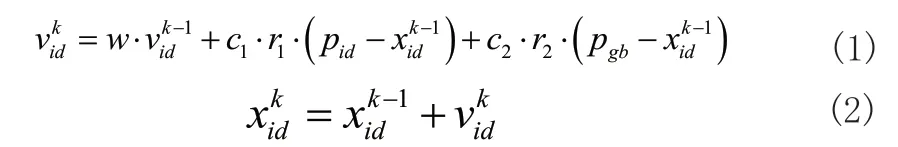
本章中提出的是自适应权重粒子群优化算法,其是在粒子群算法的基础上引入非线性动态惯性权重系数ω,其表达式如式(3)所示:
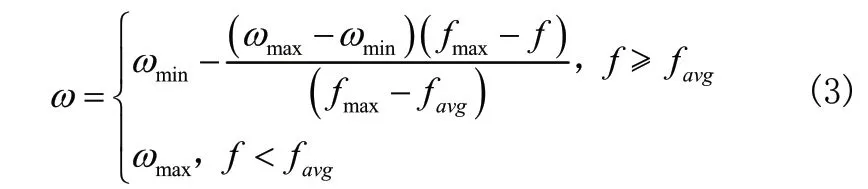
其中ωmin、ωmax为惯性权重最小值和最大值,fmax、favg为粒子最大适应度和平均适应度,ω值随着粒子适应度值变化而变化,因此称为自适应权重[10]。
在使用自适应权重粒子群算法时,应先将粒子的速度和位置初始化,然后计算适应度f的值来得到粒子的位置,直至找到最佳值[15]。流程图如图7所示。

图7 自适应权重粒子群算法应用流程图
2.2 仿真结果
为使仿真过程简单,假定相位完全匹配,本文只考虑对准误差对耦合效率的影响,因此耦合效率表达式为[16]:

w0为z=0时光纤的模场半径,wf0为芯片的感光半径径,当芯片和光纤的距离是z时,模场半径表达式为:

dx、dy为横向偏移,z为纵向偏移,θx、θy为角度偏移,λ为传输光中心波长。
本文选取爬山法与其对比,对两算法设置相同的初始条件:
1)误差范围:dx、dy为40um,z为80um,θx、θy为5°;
2)模场参数:λ=850nm,w0=5um,wf0=25um;
3)运动平台精度:线性运动0.1um,角度旋转0.001°。
爬山法仿真参数如表1所示。

表1 爬山法仿真参数
自适应权重粒子群算法仿真参数如表3所示。

表3 自适应权重粒子群算法仿真参数
基于以上仿真参数,分别用爬山法和自适应权重粒子群算法进行耦合相率仿真,仿真结果如图8所示。

图8 算法对比
通过分析上图仿真结果,在同种条件下,自适应权重粒子群算法迭代次数仅为25次,而爬山法迭代次数多达80次,相比之下,自适应权重粒子群算法的耦合效率明显优于爬山法。
2.3 实验结果
为比较在实际应用中爬山法和自适应权重粒子群算法的耦合效果,本节针对两种算法进行实验。耦合系统已固定角度方向偏移,因此本实验只需考虑横向偏移X、Y以及纵向偏移Z。采用20组COB光模块组件在耦合对准系统下进行实验,其过程为:
1)将每组光模块手动耦合至功率最大值处。
2)经过运动平台步进,将Lens适配器分别沿X、Y、Z方向随机移动一定距离(40um范围内)。
3)分别用爬山法和自适应权重粒子群算法在相同位置开始耦合,记录光发射端和接收端的耦合时间以及成功/失败的次数。
实验结果如表4所示。
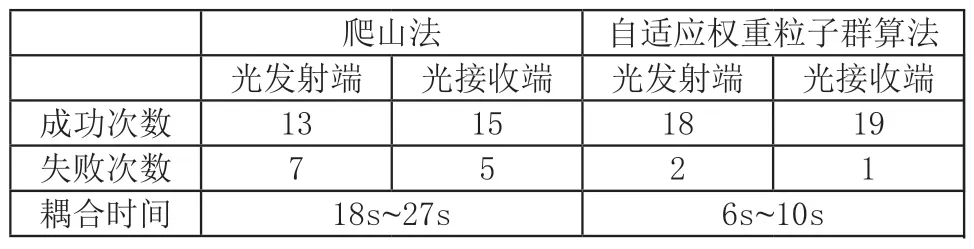
表4 两种算法的实验结果对比
分析上述实验结果可以看出,自适应权重粒子群算法的耦合成功率较高,可达92.5%,相比于爬山法的耦合成功率(70%)提高了32%。并且在搜索效率上自适应权重粒子群算法也较快,仅需6~10秒,相比于爬山法的耦合时间(18-27秒)加快了44%以上。
2.4 结果分析
爬山法属于数值解法,原理简单,在激光器和光纤的对准问题上已经有了很多应用,但是在耦合对准过程中一次只能进行单维度搜索,搜索速度较慢,成功率不高,不能克服每个自由度之间的耦合误差,容易陷入局部最优的误区。
通过2.2节仿真曲线分析,自适应权重粒子群算法在前期耦合速度很快,迭代6次就达到了耦合效率80%的位置,虽然后期耦合速度相对偏慢,但是迭代25次后耦合效率就达到100%,耦合速度明显优于爬山法。自适应权重粒子群算法在迭代过程中更倾向于全局搜索,避免粒子群向最优的位置集中,使粒子群较为离散的分布在整个区域,能很好避免局部优值,在解决复杂的优化问题中表现出了良好的性能。
3 结语
COB光模块的耦合对准是封装工艺的关键步骤,也是技术难点,耦合质量直接影响到光模块的良品率。本文分析了耦合对准原理,并经过实验理论分析了对准误差对耦合效率的影响;在此研究和分析的基础上,提出了自适应权重粒子群算法,并与爬山法进行仿真和实验对比,得出结论:自适应权重粒子群算法使得COB光模块的耦合速度和耦合成功率大幅提升,在X、Y、Z三个自由度的耦合成功率较高(92.5%),与爬山法相比提高了32%。在搜索效率上自适应权重粒子群算法也较优,仅需6-10秒,与爬山法相比加快了44%以上。由于自适应权重的引入,粒子群算法在平衡全局和局部搜索的优化问题上,比爬山法更加智能和准确。

