基于关联规则的库岸边坡监测数据挖掘方法

陈 波，詹明强，黄梓莘

(1.河海大学 水利水电学院，南京 210098； 2.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098； 3.中国电建集团中南勘测设计研究院有限公司，长沙 410014)

1 研究背景

库岸边坡的运行稳定对于水利工程的服役安全至关重要，其失稳灾害会对工程自身效益和周边生命财产安全造成巨大损失。研究表明，库岸边坡失稳破坏会经历渐变到突变的累进发展过程，而边坡运行监测资料记录了失稳灾害孕育的全过程信息，尤其是失稳破坏发生的前兆信息，有必要结合监测资料开展库岸边坡的安全监控和灾变预警研究。在库岸边坡工程安全监测过程中，必然会产生海量与边坡稳定相关的数据信息，关联规则正是运用统计学有关原理，寻找不同属性数据间隐蔽的相互关系，较为广泛地应用于水利工程的知识发现。

近年来，学者们对边坡安全监测数据挖掘方法展开了研究。张治强等[1]考虑到边坡地形、岩体等影响因素，应用Apriori算法构建边坡稳定性和破坏方式的智能预测模型。马水山等[2]运用经典频集算法对滑坡监测资料进行关联规则挖掘，得到了滑坡变形与监测数据之间的关联规则。刘小珊等[3]基于大量边坡工程失稳破坏全过程的监测数据，采用Apriori算法揭示了边坡累积位移和累积速率在不同失稳演化阶段的特征。揭奇等[4]针对分布式光纤传感(DFOS)的边坡多场监测资料开展关联挖掘，发现了库水位和地下水位监测序列之间的蕴含的潜在关联特征。王林伟等[5]提出了一种基于Apriori的边坡岩体变形特征关联分析方法，根据关联规则挖掘分析了边坡岩体变形的主要成因。赵久彬等[6]提出了前后部项约束关联规则并行化算法，深入总结了典型滑坡和区域滑坡的危险性规则。段功豪等[7]研究了堆积层滑坡的形成和演化原理，结合聚类分析和关联规则算法快速提取边坡监测数据的实时变形特征，为滑坡灾害的预测预报提供了参考依据。Zhao等[8]采用灰色关联方法探寻了边坡位移与库水位、降雨量、外部气温等因素间的相关性，研究结果表明倾覆岩边坡存在水动力失稳的可能性。

通过总结上述运用关联规则时空数据挖掘算法在库岸边坡监测资料分析的研究现状可以看出，目前针对动态多方位的实时监测数据的挖掘工作开展较少，同时监测数据关联规则挖掘多采用Apriori算法。然而，在Apriori算法搜索过程中，不仅需要重复扫描数据库而且需要处理大量候选频繁项集，在应对海量、长模式或密集型的数据时，不可避免会暴露出时间效率低、空间压缩性差等弊端。基于此，本文采取改进的关联规则算法FP-Growth对多测点和多项目的监测数据展开挖掘，从大量看似无规则的原始监测数据中获取有效判别信息，从而为后续边坡运行的安全预警研究提供方向性指导。

2 关联规则算法原理

2.1 关联规则定义

假设存在事务集合C={c1，c2，…，cn}，ci(i=1，2，…，n)，将关联规则的具体定义介绍如下[9-10]。

2.1.1 关联规则

设A={a1，a2，...，aj}，B={b1，b2，...，bk}，(1≤j，k≤i)，若存在A⊂C，B⊂C，且A∩B≠∅，则说明项集A和B各自为事务集合C中的两个项集。此时，根据项集A和B构建形如A=>B的关系，即被称为关联规则。在关联规则A=>B中，前项A可视为关联规则的条件，后项B可视为关联规则的结论。

2.1.2 支持度

在事务集合C中，包含A∩B的事务即同时包含项集A和B的事务占全部事务的比重，称为事务集合C中关联规则A=>B的支持度，则有

(1)

2.1.3 置信度

在事务集合C中，包含A∩B的事务占包含A事务的比重，称为事务集合C中关联规则A=>B的置信度Conf，则有

(2)

2.1.4 强关联规则

在事务集合C中，设置min_Supp和min_Conf为指标阈值，当关联规则A=>B同时满足Supp(A=>B)≥min_Supp和Conf(A=>B)≥min_Conf两个条件时，称关联规则A=>B为强关联规则。

2.2 FP-Growth算法原理

FP-Growth算法是一种在不产生候选项目集的前提下挖掘出全部频繁项集的方法，关键在于利用归纳分散策略将事务数据库以频繁模式树FP-Tree的形式重构[11]。FP-Tree在压缩存储数据量级的同时保留关联信息，显著缩小算法搜索范围，有效避免关联组合爆炸，能够改善边坡监测数据挖掘运行速度慢的问题。

结合图1的算法原理，将FP-Growth算法主要步骤介绍如下。

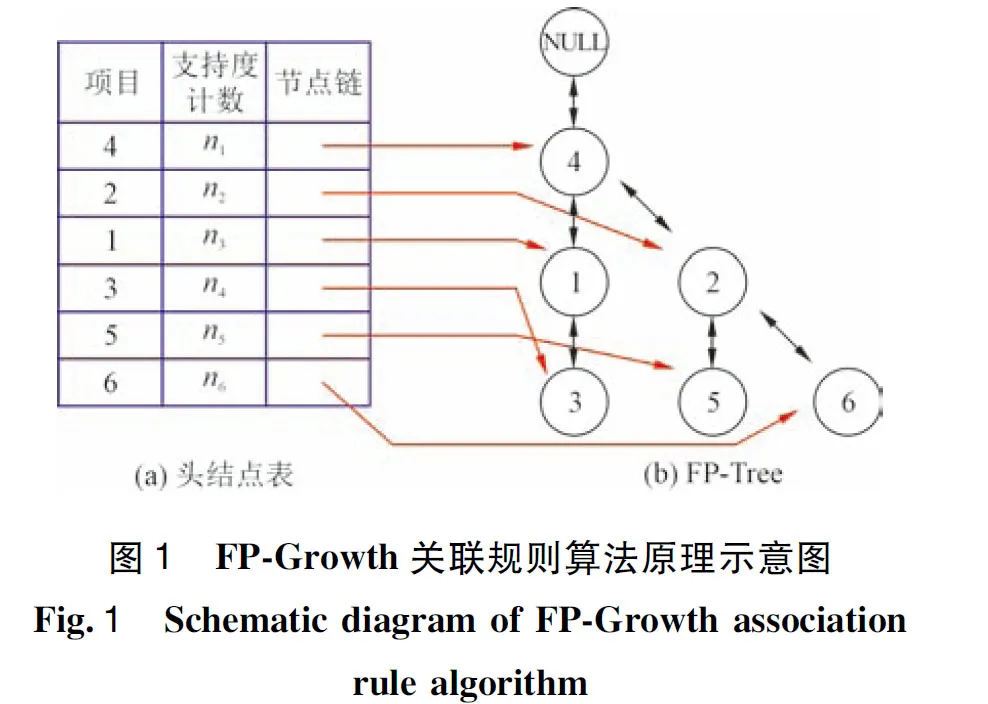
2.2.1 整体扫描数据库

整体扫描事务数据库，分别计算各项目的支持度指标，接着根据设定阈值min_Supp筛选出其中所有频繁项集，并按照支持度计数从大到小对频繁项集进行排序，形成频繁项表L(图1(a)中的头结点表)。

2.2.2 二次扫描数据库

二次扫描事务数据库，利用搜索出的所有频繁项集构造如图1(b)所示的FP-Tree，首先创造FP-Tree的根节点Null，接着按照频繁项表L的排列次序，将频繁项集依次插入FP-Tree中的每个分支中。

2.2.3 创建头节点表

为方便搜索FP-Tree，创建如图1(a)所示的头节点表，目标在于让每个频繁项集能通过红色箭头所示的结点链与FP-Tree的树结点位置相连。

2.2.4 挖掘关联规则

利用头节点表和树结点的链接，采用自底向上的方式对Priority树进行关联规则的挖掘。

3 基于FP-Growth算法的边坡关联规则挖掘

考虑到FP-Growth算法在计算效率上的优越性，本文基于FP-Growth算法，分别从因果关联规则挖掘和空间关联规则挖掘2个角度，对多测点多项目的边坡时空监测数据开展关联规则挖掘工作。结合图2的算法流程，将主要步骤介绍如下。

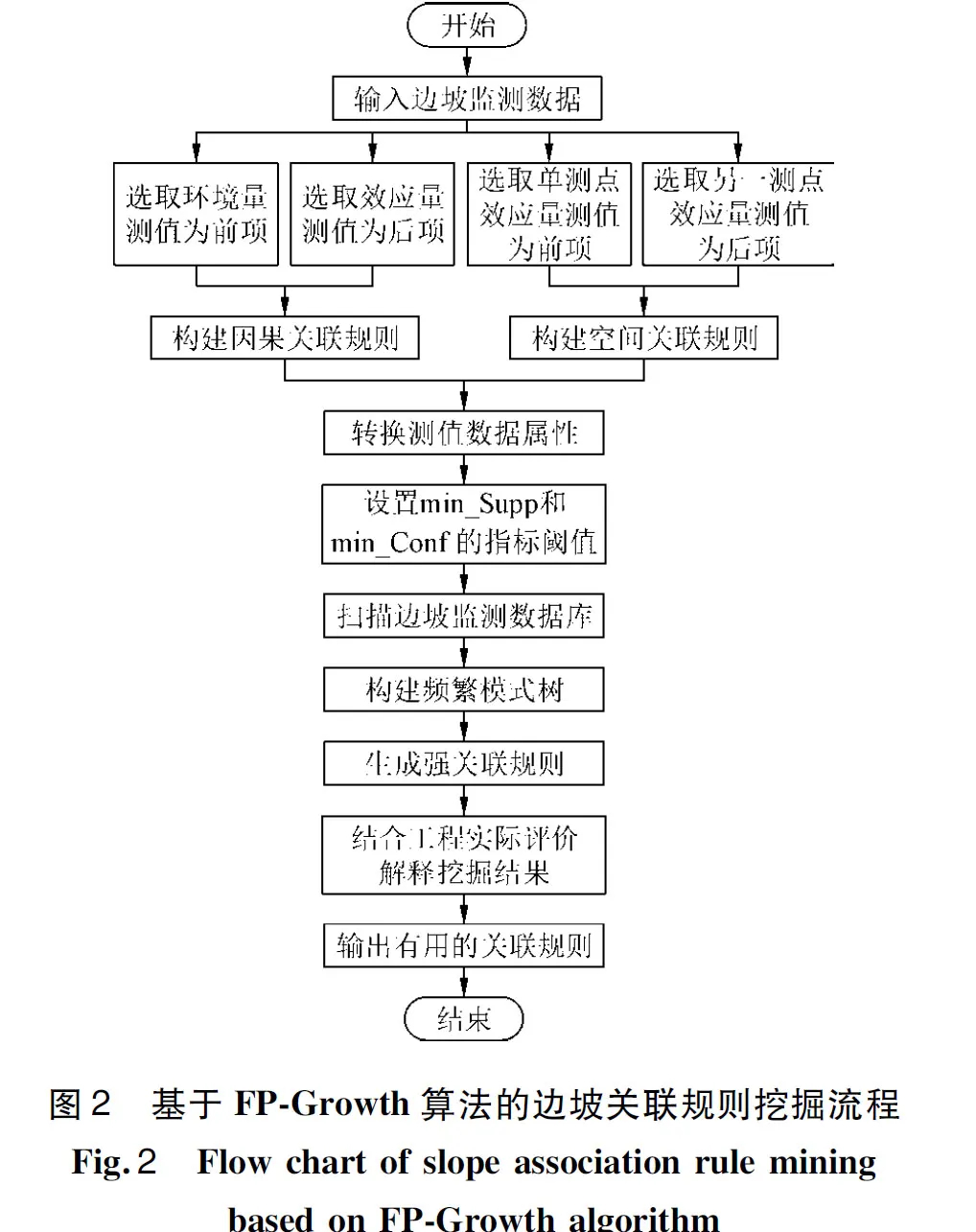
3.1 规则前后项设置

3.1.1 因果关联规则挖掘

探究环境量和效应量之间兼具的因果性和关联性，针对边坡监测数据进行因果关联规则挖掘。根据领域内专家经验可知，降雨和库水作为边坡失稳诱因之一，主要通过软化、饱水加载、静水压力、动水压力4种作用造成边坡变形[12]。因此，基于降雨量测值、库水位测值、气温测值等监测环境量数据设置关联规则的前项X，同时以位移测值、渗流测值等监测效应量数据作为关联规则的后项Y的设置依据。

3.1.2 空间关联规则挖掘

针对边坡监测数据探寻不同空间位置测点测值数据的潜在联系，开展空间关联规则挖掘。边坡效应量的监测数据由多个测点测值组成，这些测点各自具有不同的空间位置，在关联规则挖掘过程中引入对空间位置的考虑，更有助于深入了解边坡整体结构和内在规律。以监测效应量数据为基础设置规则前项和后项，前项X表征某一监测项目的测点测值变动情况，后项Y表征同时刻同一监测项目另一测点的测值变动情况。

3.2 测值数据属性转换

在关联规则挖掘开始之前，还需要将数据变化程度、数据离散情况依据现有监测水平诠释为简明易懂的定性语言，原因在于每个边坡监测数据都是一个精确的定量数值，无法反映任何定性信息，同时以连续数值形式表示的测值序列也不方便直接参与计算。因此需要实现测值数据的属性转换，具体做法是在不破坏数据分布的前提下，将数据值域划分成若干个区间组合，并分别赋予不同区间以明确的物理含义。

假设边坡存在一固定特征，包含该特征的n个测点组成项集集合xi，i=1，2，…，n，则项集集合xi在所有项集集合xj(j=1，2，...，m)中的贡献占比D=n/m。

基于等距分箱思想[13]，结合贡献占比极值Dmax和Dmin，将贡献占比D等距划分为3类，依次取得三级划分点，形成区间等差数列为：

d=(Dmax-Dmin)/3 ；

(3)

(4)

根据三级划分点生成不同贡献占比的项集集合区间，包括：低贡献占比的项集集合区间为[a1，a2)，中贡献占比的项集集合区间为[a2，a3)，高贡献占比的项集集合区间为[a3，a4]。通过判断边坡测值数据的区间属性，可以实现测值数据的属性转换。

3.3 构建频繁模式树

在进行测值数据的属性转换之后，在保留项集信息的基础上构造边坡时空数据挖掘的Priority树，采用自底向上的方式全面扫描数据库，筛选出在min_Supp和min_conf两个阈值约束下的关联规则，即生成强关联规则。

3.4 生成边坡关联规则

最后，对照工程实际运行情况对生成规则进行逐一评价和解释，诠释所筛选规则内含的物理现象本质，从而在边坡时空监测数据中挖掘出反映工程运行性状的有效信息。

4 工程实例

本文研究边坡位于某拱坝库首左岸，是该拱坝的近坝边坡，距离大坝600～1 300 m，顺河方向长700 m，相对坡高500～700 m。高度1 400 m以上平均坡度25°～45°，高程1 400 m以下22°～25°，并有多级缓坡地段。坡面走向约S60°E，岩层产状近EW/S∠30°～35°，边坡为二元结构的单斜顺向坡。由于边坡沿河各段的稳定程度不一，根据边坡岩性特征、边坡地质构造和失稳破坏模式的不同，将1 400 m 高程以下的边坡自上游向下游分为Ⅰ、Ⅱ、Ⅲ区，如图3所示。

自1985年以来，经历前期勘察、大坝施工、水库蓄水及工程运营等多个时期，边坡积累了包含地表变形、深层变形和环境量的大量监测资料，现有监测信息汇总如表1所示。

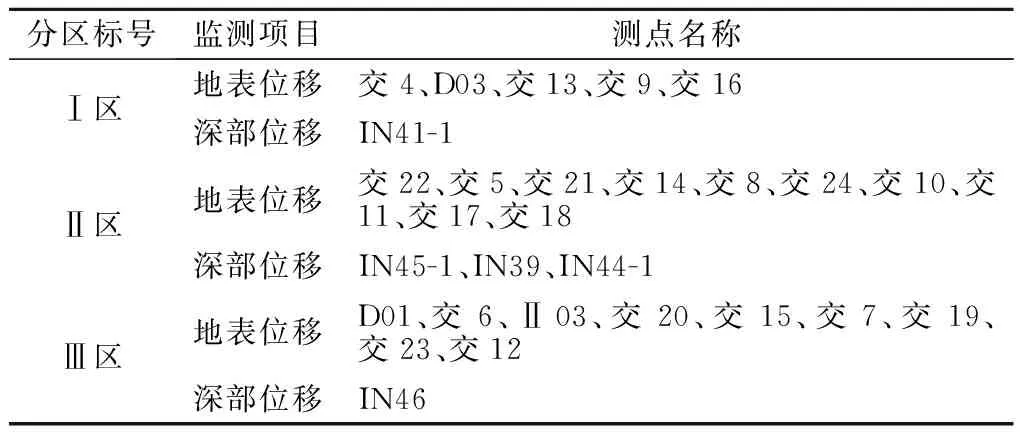
表1 研究边坡的监测信息

4.1 边坡监测资料的预处理

在开展边坡监测信息时空数据挖掘工作前，首先采用箱线图对边坡原始监测资料进行异常值确定。根据箱形图的定义，箱子的长度代表四分位数的间距(IQR)，箱两端分别是上四分位数(Q3)和下四分位数(Q1)。箱形图定义的异常值指样本数据大于上限(Q3+1.5IQR)和小于下限(Q1-1.5IQR)。

首先根据箱线图的内外限分布，以及上下四分位数距，直观判断原始监测信息的对称性、离群测值和极端测值的分布情况。

观察边坡位移监测信息的箱线图(图4)可以看出：对比3个方向的位移监测数据，其中以顺坡向位移监测数据的集中趋势最显著，顺坡向、垂直向和顺河向3个方向位移监测数据的集中趋势依次递减；综合测点区域分布结果，3个区域的位移监测数据整体离散程度比较相似。在极值识别的基础上，根据箱线图定义对异常测值进行处理，此处将异常值全部剔除，同时采用3次样条插值法填补监测序列中的缺失值，为后续关联分析的时空数据挖掘工作开展奠定基础。

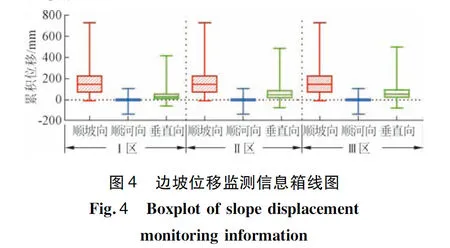
4.2 边坡监测信息的关联分析

基于FP-Growth算法对边坡监测数据进行关联分析，关键在于边坡监测数据前后项的设置，本节主要选取环境量与效应量的监测数据作为构建关联规则X=>Y前、后项的基础，分别从因果关联和空间关联2个角度开展边坡监测信息关联挖掘和知识发现。其中，环境量数据来源于库水位的监测数据，效应量数据来源于位移测点顺坡向、顺河向、垂直向的位移监测数据，以及钻孔测点的地下水位监测数据。

在关联分析开始之前，首先需要对各测值数据进行属性转换处理，运用相应数学统计量表征测值数据的时序分布情况和变动剧烈程度，然后采用等差数列依次取得三级划分点，将各部分数据进行等距区间划分和名称转换。以库水位数据的属性转换为例，假设库水位数据H∈[Hmin，Hmax]，分别取得区间三级划分点H1、H2、H3、H4，当H∈[H1，H2)时，命名为“低水位”，当H∈[H2，H3)，命名为“常水位”，当H∈(H3，H4]时，命名为“高水位”。

进行测值数据的属性转换之后，在保留项集信息的基础上构造边坡时空数据挖掘的Priority树，并采用自底向上的方式全面扫描数据库，筛选出符合工程实际的强关联规则。

4.2.1 边坡监测信息的因果关联规则挖掘

4.2.1.1 库水位时序分布与钻孔水位的因果关联规则挖掘

计算库水位时序分布与钻孔水位时序分布的因果关联规则X1=>Y1，首先设置前项X1为监测环境量，即库水位的时序分布情况，设置后项Y1为监测效应量，即43#、44#、45#钻孔水位的时序分布情况。在进行属性转换后，规则前项为形如X1={高水位，常水位，低水位}的项集集合，规则后项为形如Y1={高钻孔水位，常钻孔水位，低钻孔水位}的项集集合。在此基础上，开展因果关联规则X1=>Y1的挖掘工作。运用FP-Growth算法进行关联规则挖掘，所筛选出的强关联规则计算结果如表2所示，关联规则挖掘示意图如图5所示。

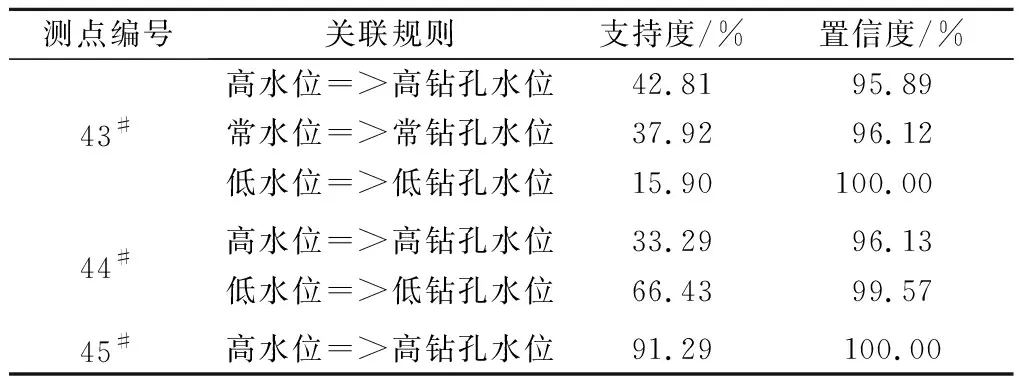
表2 X1 =>Y1的关联规则计算结果

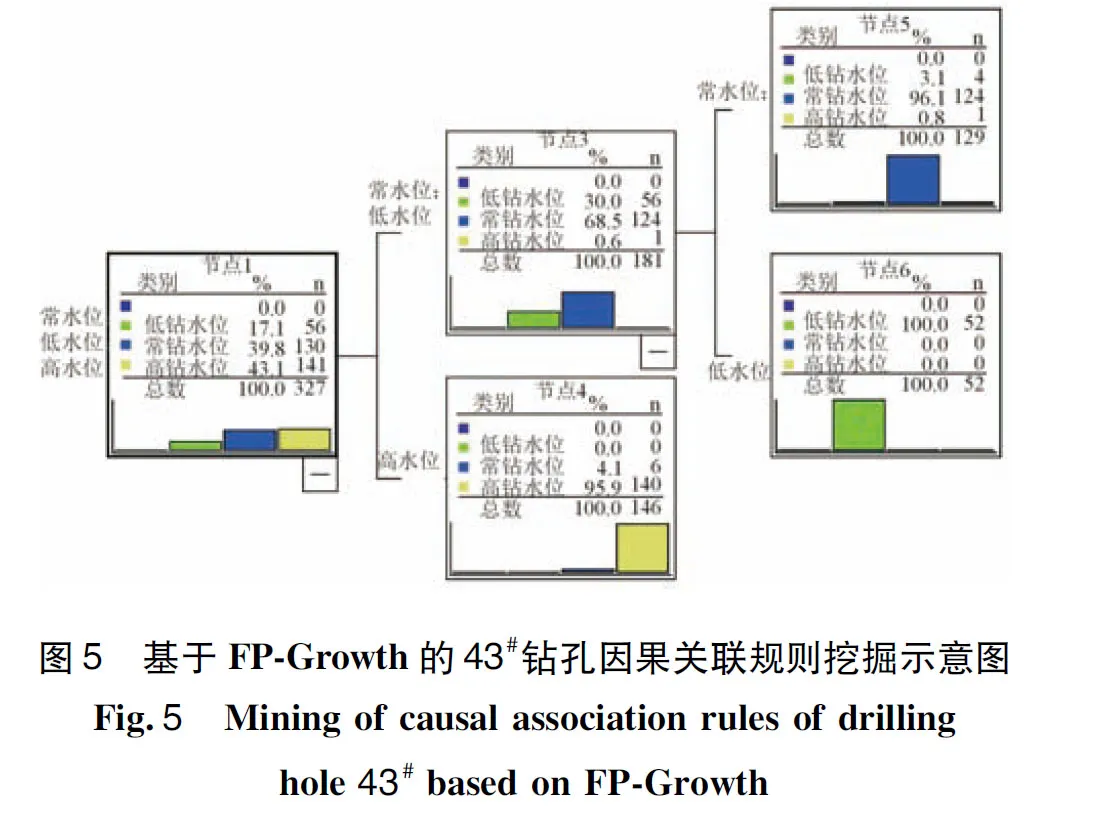
综合上述基于43#、44#、45#测孔监测数据获得的关联规则挖掘结果，可以得出如下结论：

(1)从置信度角度可以看出，所提炼的关联规则置信度均超过95%，最大置信度达到100%，规则的可靠程度和可信程度较高，可得出钻孔水位高程的时序分布情况与库水位的时序分布情况关联程度高的结论，说明了监测数据的可靠性。

(2)从支持度角度可以看出，43#钻孔水位不同高程的时序分布较为均匀，而45#钻孔水位高程则基本位于高水位区间，支持度达到91.29%。

根据工程经验知识可知，地下水位的时序分布和库水位的时序分布具有因果效应，而上述基于FP-Growth的关联规则挖掘结果表征地下水位高程的时序分布还与库水位的时序分布具有显著关联效应，说明边坡地下水位受库水位升降影响，岩体渗透性较好。

4.2.1.2 库水位与位移测值的因果关联规则挖掘

计算库水位变动剧烈程度与位移测值变动剧烈程度的关联规则X2=>Y2，设置前项X2为库水位的测值变动程度，设置后项Y2为边坡Ⅰ区、Ⅱ区和Ⅲ区位移的代表测点(交8、交9、交12)3个方向(顺坡向、顺河向、垂直向)位移测值的变动程度。此时，规则前项为形如X2={水位变动小，水位变动中等，水位变动大}的项集集合，规则后项为形如Y2={测值变动小，测值变动中等，测值变动大}的项集集合。在此基础上，采用FP-Growth算法开展因果关联规则X2=>Y2的数据挖掘工作。所筛选出可信程度较高的因果关联规则如表3所示。

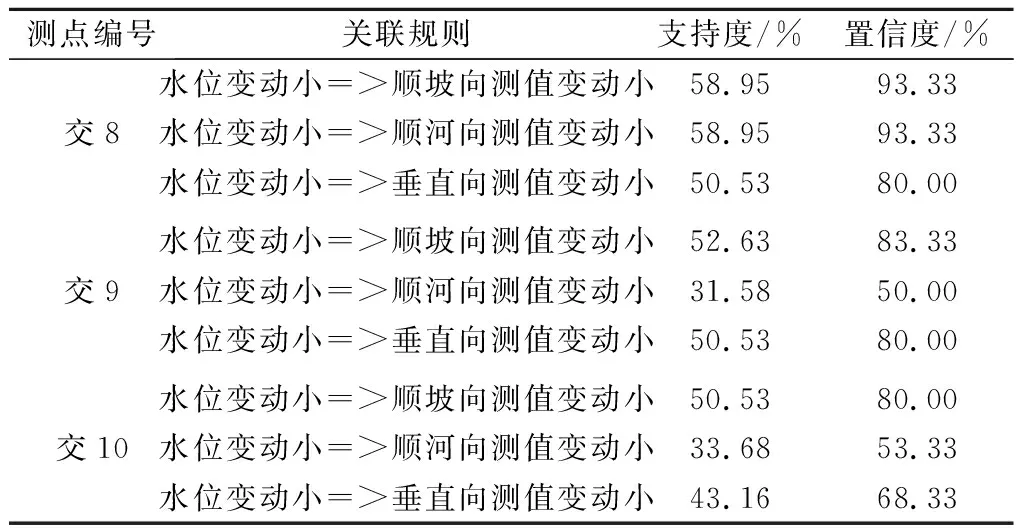
表3 X2 =>Y2的关联规则计算

分析上述计算结果，得出如下结论：

(1)对比不同监测项目，可以看出三向位移测值与库水位的关联程度明显低于地下水位与库水位的关联程度，原因在于位移测值受到温度、水位、降雨等因素的综合影响，而地下水位高程则主要受到库水位的影响。

(2)对比不同分布区域，在边坡Ⅰ区、Ⅱ区和Ⅲ区代表测点中，边坡Ⅱ区的交8测点位移测值变动对于库水位的测值变动程度较为敏感，3个方向对应的置信度分别为93.33%、93.33%、80.00%，表征关联规则的可信程度较高。

(3)对比不同位移方向，顺坡向位移测值变动与库水位测值变动关联程度最高，3个测点对应的规则置信度分别为93.33%、83.33%、80.00%，因此可以得出顺坡向位移测值变动受库水位影响最大的结论。

(4)从支持度水平还可以看出，三向位移测值的变动程度均较小，与目前边坡变形相对稳定但存在缓慢增长趋势的稳定性分析结论相吻合。

为计算库水位状态和库水位变化二维变量与边坡位移之间的关联规则X3=>Y3，规则前项为形如X3={低水位时水位降低，低水位时水位升高，常水位时水位降低，常水位时水位升高，高水位时水位降低，高水位时水位升高}的项集集合，规则后项为形如Y3={位移速率升高，位移速率降低}的项集集合。位移速率指的是两次采集数据期间发生的位移变化量除于采集间隔的天数，得到的平均变化速率。考虑到交8测点顺坡向位移变动受库水位影响最大，筛选出交8顺坡向可信程度较高的因果关联规则如表4所示。

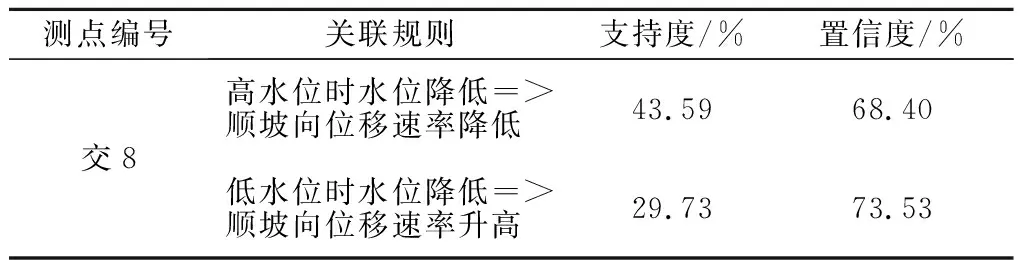
表4 X3 =>Y3的关联规则计算

从置信度水平可以看出库水位处于低位时比处于高位时，水位降低对位移速率和边坡稳定性的影响更大。当库水位处于低位且库水位降低时，对边坡的稳定是最不利的。库水位的变化对边坡稳定性的影响可以理解为：当库水位下降时，边坡将出现临空面，坡体内部渗透压力差、水力梯度增大，易导致边坡失稳。

由上述分析可以看出，因果关联规则挖掘能够抽取并挖掘环境量和效应量之间的关联性和因果性，可以为工程安全监控理论提供一个全新视角。

4.2.2 边坡监测信息的空间关联规则挖掘

计算多个位移测点测值发展规律间的关联规则X4=>Y4，设置前项X4为一测点的测值发展规律，设置规则后项Y4为另一测点的测值发展规律，此处选取交10、交8、交12、交13、交16、交5、交6、交7、交9、交11、交14、交15共12个位移测点1998—2019年的三向监测数据进行关联规则计算。此时，规则前项为形如X4={测点1测值小，测点1测值中等，测点1测值大}的项集集合，规则后项为形如Y4={测点2测值小，测点2测值中等，测点2测值大}的项集集合。在此基础上，采用FP-Growth算法开展关联规则X4=>Y4的数据挖掘工作。所筛选出可信程度较高的空间关联规则如表5、图6所示。

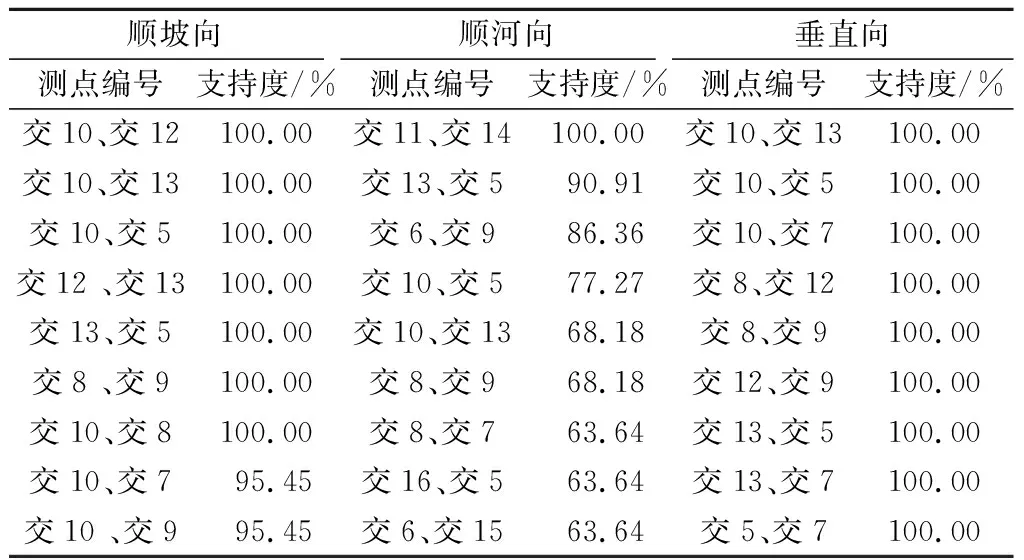
表5 X4=>Y4的关联规则计算

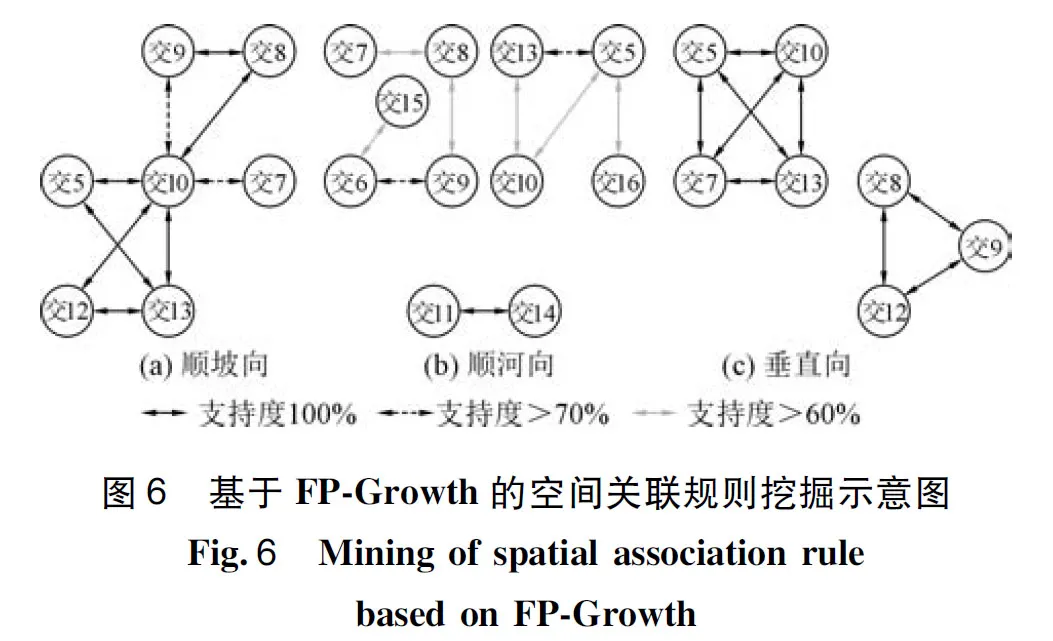
综合上述基于3个方向测值数据计算获得的空间关联规则，可以看出：

(1)3个方向的测值数据中，顺河向的测点同步变化程度普遍较低，而顺坡向和垂直向呈现了显著的测点同步变化趋势。

(2)测点交10、交5和交13三个测点在三个方向的测点变化同步程度都很高。其中，测点交10和交5三个方向变化同步支持度分别为100%、77.27%、100%，测点交13和交5三个方向变化同步支持度分别为100%、90.91%、100%，测点交10和交13三个方向变化同步支持度分别为100%、68.18%、100%。

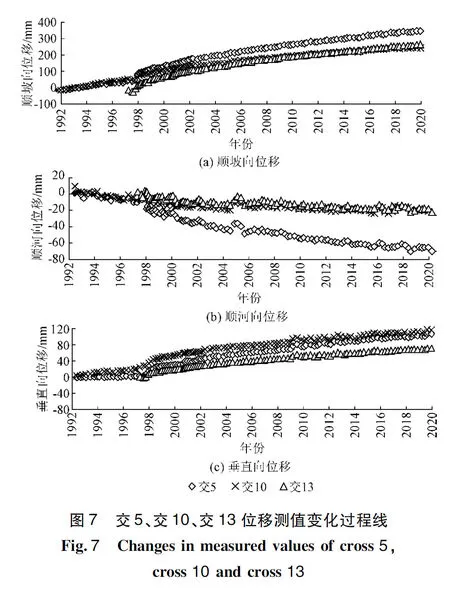
在计算得出不同测点空间关联规则的基础上，对比交10、交5和交13三个测点在不同方向的测值变化过程线对输出规则加以验证，如图7所示。从图7可以看出：3个方向的位移测值增减趋势比较一致、变化范围大体相同，由此判断输出规则可信程度比较高。

在空间关联规则挖掘过程中，衡量不同测点的变化同步程度，并筛选出其中变化同步程度较高的关联测点。利用这些测点间的空间关联规则，当部分测点监测数据缺失时，可以参考另一个或几个同步变化置信度高的关联测点来修复空缺数据；当同步置信度高的2个关联测点的变化出现较大差异时，应提出疑似异常信号，以保证库岸边坡的安全服役。

5 结 论

针对库岸边坡监测数据隐含的时空关联关系，结合工程实际，研究了关联规则的数据挖掘方法，对多测点多项目的海量边坡监测信息开展时空数据挖掘工作，所得主要结论如下：

(1)分别考虑环境量和效应量之间的关联性和因果性，并考虑不同空间位置测点测值变动情况的关联性，挖掘了边坡时空监测数据中潜藏的因果关联规则和空间关联规则。可以看出，因果关联规则挖掘能够抽取并挖掘环境量和效应量之间的关联性和因果性，可以为工程安全监控理论提供一个全新视角；空间关联规则挖掘可以汇总生成服务于边坡健康工作的规则集合，相关关联测点也可以用来相互参考测值变化趋势和互为补充缺失测值。

(2)FP-Growth算法新颖、思路清晰、结果简约、实用性强，实例表明，FP-Growth算法为库岸边坡监测数据挖掘提供一条良好思路。

(3)本文对库岸边坡潜在的关联规则进行了初步研究，但仍有一些内容需要深入研究，如监测数据的可靠性与规则的支持度、置信度之间的影响；库岸边坡出现异常行为时，监测数据给出的各种结构响应之间的相关性验证。