抗滑桩加固边坡三维稳定因素的敏感性分析

侯超群, 丁 莹, 孙志彬, 李见飞

(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)

无论是理论分析还是工程实践,边坡稳定性分析都是岩土工程中的重要课题,受到研究人员的持续关注。已有相关研究中常将其视为二维问题[1-4],当边坡具有足够的宽度,符合平面应变条件时,二维稳定性分析能够满足工程需要;但实际工程中边坡两侧常被地形、人工构筑物约束而宽度受限,致使边坡破坏具有明显的三维特征,此时二维分析会低估边坡稳定性能,导致设计过于保守。

为满足工程需要,有必要对边坡的三维稳定性进行评估。边坡的三维稳定性分析方法可分为极限平衡法与极限分析法。应用极限平衡法时常需要对滑动块体进行条分,并在应力简化的基础上建立平衡方程[5-8];利用该方法进行三维分析时需要划分的土条数较多,导致求解的方程数量相应增加,求解过程较为繁琐。极限分析法能够充分考虑土体的塑性特征,不需要进行块体划分及应力简化,并在速度相容或静力平衡的条件下求得边坡临界载荷的严格上、下限解。一般地,相对于极限分析下限解,上限解的求解更加方便,在边坡稳定性分析中的应用也更普遍。

基于上限法,文献[9]构建“牛角型”的边坡三维旋转破坏机构,并研究了普通土质边坡的三维稳定性问题。近年来该机构的应用得到了一系列拓展:文献[10]采用该机构评估渗透力作用下土质边坡的三维稳定性;文献[11]考虑土强度非线性和剪胀的共同影响,结合该机构分析地震条件下二级边坡的三维稳定性;文献[12]运用该机构研究两级土质边坡的三维稳定性问题。

当稳定性不足时,边坡有失稳或滑塌的风险。为提高边坡安全性能、降低事故风险,需对边坡进行加固处理。抗滑桩作为常见的加固手段,因其支挡效果好、服役稳定性佳的特点而被广泛采用。对抗滑桩加固边坡进行三维稳定性分析,具有显著的工程意义。基于极限分析上限定理,文献[13]研究抗滑桩位置及尺寸对边坡三维稳定性的影响;文献[14]研究在非均质及各向异性条件下抗滑桩对边坡稳定性的影响,并给出边坡安全系数的设计图表。

上述研究表明，抗滑桩边坡的三维稳定性受边坡几何形状、土体强度参数、抗滑桩参数、地震作用(尤其是高烈度地震区)等多种因素的影响。实际上，不同因素对边坡三维稳定性的影响程度均不相同,进行稳定性设计时也不能同等对待，可采用敏感性分析对边坡稳定性的影响因素进行系统评估。文献[15-17]针对二维情况进行了研究,对抗滑桩边坡三维稳定性的敏感性研究很少。

由于实际工程中多级边坡较为常见,本文以抗滑桩加固的两级边坡为例进行三维敏感性分析。首先利用三维上限机构建立抗滑桩边坡的稳定性分析模型;然后运用正交分析法,研究地震条件下各参数的敏感性顺序,并简要分析各因素对边坡安全系数的影响规律;最后根据分析结果,提出相应的工程建议。

1 边坡稳定性分析

1.1 破坏机制

边坡及“牛角型”三维旋转破坏机构如图1所示,边坡破坏机制三维示意图如图2所示。

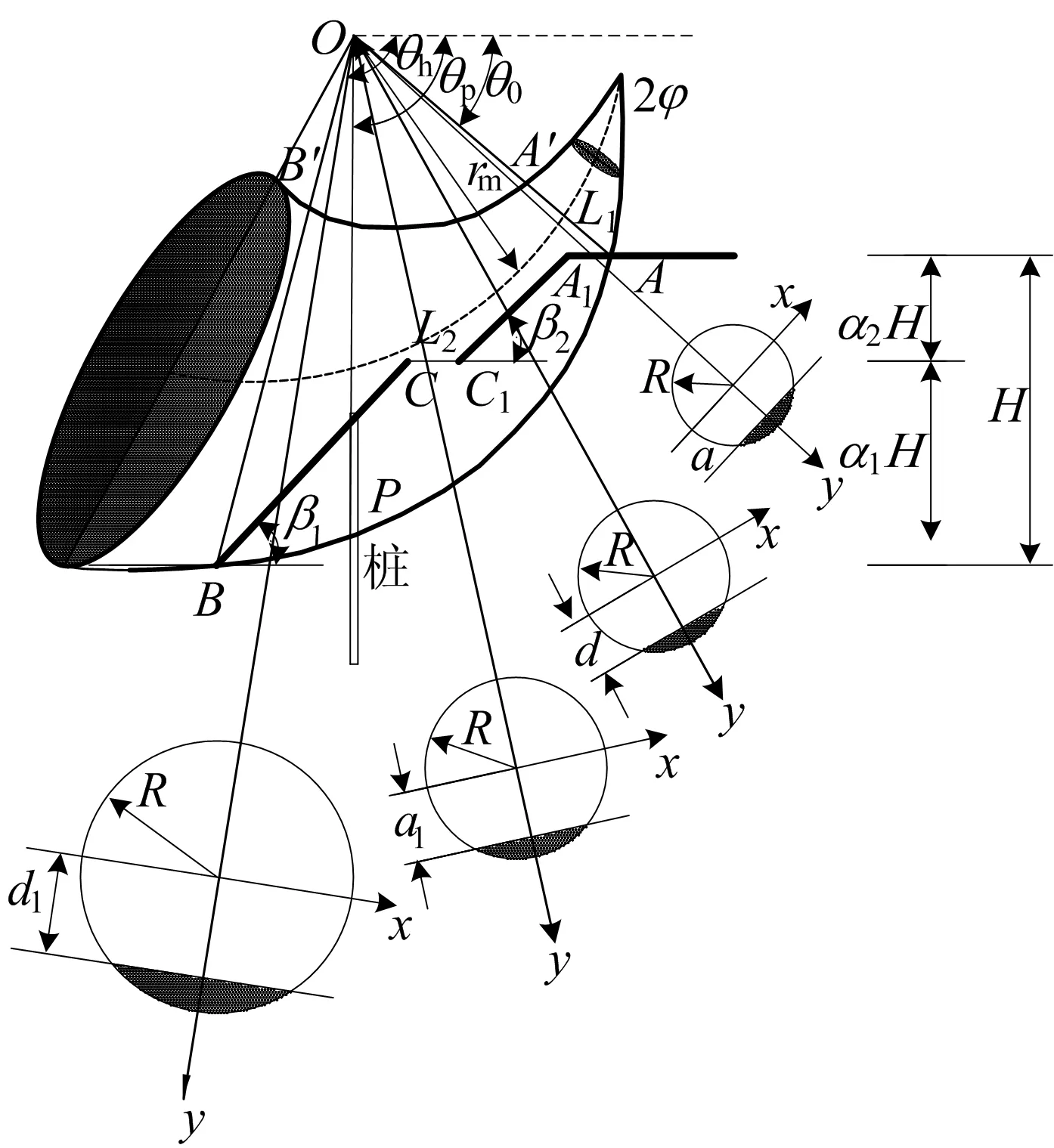
图1 “牛角型”三维旋转破坏机构

图2 边坡破坏机制三维示意

边坡倾角分别为β1、β2,边坡高度为H,α1、α2为高度系数[12],且α1+α2=1,基线OA、OB的长度、倾角分别为r0、θ0和rh、θh,AA1的长度为L1,平台CC1的长度为L2。

本文采用的三维破坏机构由顶角为2φ的“牛角型”曲线圆锥构成,圆锥对称剖面的上、下边界分别为对数螺旋线A′B′、AB。破坏面上部土体围绕O点旋转,角速度为ω,破坏面下部土体保持不变。

AB的表达式为:

r=r0exp[(θ-θ0)tanφ]

(1)

A′B′的表达式为:

r′=r0′exp[-(θ-θ0)tanφ]

(2)

其中:r0=OA;r0′=OA′;φ为土体的内摩擦角;θ为对数螺旋线AB上任一点与O点连线的倾角。

上述曲线圆锥机构的破坏具有明显的三维特征,但随着边坡宽度的增加,边坡破坏模式由三维逐渐向二维转变。为了反映边坡宽度对破坏特征的影响,将宽度为b的块体插入机构中,如图2a所示,该块体可看成由二维对数螺旋线机构“拉伸”而成,如图2b所示。采用插入块体后的破坏机构,能够更加准确地反映不同宽度边坡的三维破坏特征。

1.2 能耗计算

本文考虑地震力对边坡稳定性的影响,因此破坏机构的总外力功率W由土体重力功率Ws和地震力功率Wk组成。

土体重力功率Ws为:

Ws=Wsoil+Wsoilb

(3)

其中:Wsoil为“牛角型”块体的重力功率;Wsoilb为插入块体的重力功率。

Wsoil的表达式为:

(4)

其中:γ为土的重度;ω为破坏机构旋转的角速度,一般取值为1 rad/s;rm=(r+r′)/2;a、d、a1、d1、x*、y*的含义如图1所示。a、d、a1、d1、x*、y*的表达式分别为:

(5)

(6)

(7)

(8)

(9)

(10)

其中,R=(r-r′)/2。

Wsoilb的表达式为:

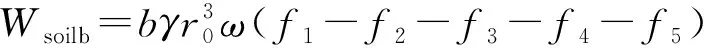
(11)

其中:f1、f2、f3、f4、f5为函数。f1～f5的表达式分别为:

sinθh)exp[3(θh-θ0)tanφ]-

(3tanφcosθh+sinθh)}

(12)

(13)

(14)

(15)

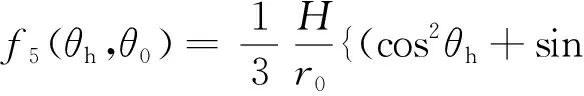
exp[(θh-θ0)tanφ]+cotβ1(cosθh+

(sinθhcotβ1)}exp[(θh-θ0)tanφ]

(16)

本文运用拟静力方法,考虑地震作用对边坡稳定性的影响,并忽略竖向地震力的作用,只考虑水平地震力的影响[11]。地震力做功功率Wk为:

Wk=Wkh+Wkhb

(17)

其中:Wkh为地震力对“牛角型”块体的外力功率;Wkhb为地震力对插入块体的外力功率。

Wkh的表达式为:

(18)

其中,kh为水平地震力系数。

Wkhb的表达式为:

(19)

其中,f6、f7、f8、f9、f10为函数。f6～f10表达式分别为:

cosθh)exp[3(θh-θ0)tanφ]-

(3tanφsinθ0-cosθ0)}

(20)

(21)

(22)

(23)

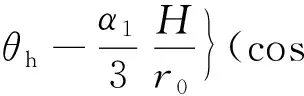
exp[(θh-θ0)tanφ]

(24)

总外力功率为:

W=Ws+Wk

(25)

考虑抗滑桩对边坡稳定性的影响,破坏机构的总内能耗散功率D由土体内能耗散功率Ds和抗滑桩引起的内能耗散功率Dp组成。

土体内能耗散功率Ds为:

Ds=Dsoil+Dsoilb

(26)

其中:Dsoil为“牛角型”块体的能量耗损功率;Dsoilb为插入块体的能量耗损功率。

Dsoil的表达式为:

Dsoil=DAA1+DA1C1+DC1C+DCB

(27)

其中,DAA1、DA1C1、DC1C、DCB为分别按坡面AA1、A1C1、C1C、CB段计算的土体内能耗散[14]。

(28)

(29)

(30)

(31)

其中,c为土体黏聚力。

Dsoilb的表达式为:

(32)

抗滑桩应力分析如图3所示。图3中:XF为抗滑桩到坡趾B点的水平距离;LX为坡趾B点到平台边C点的水平距离;θp为OP的倾角。

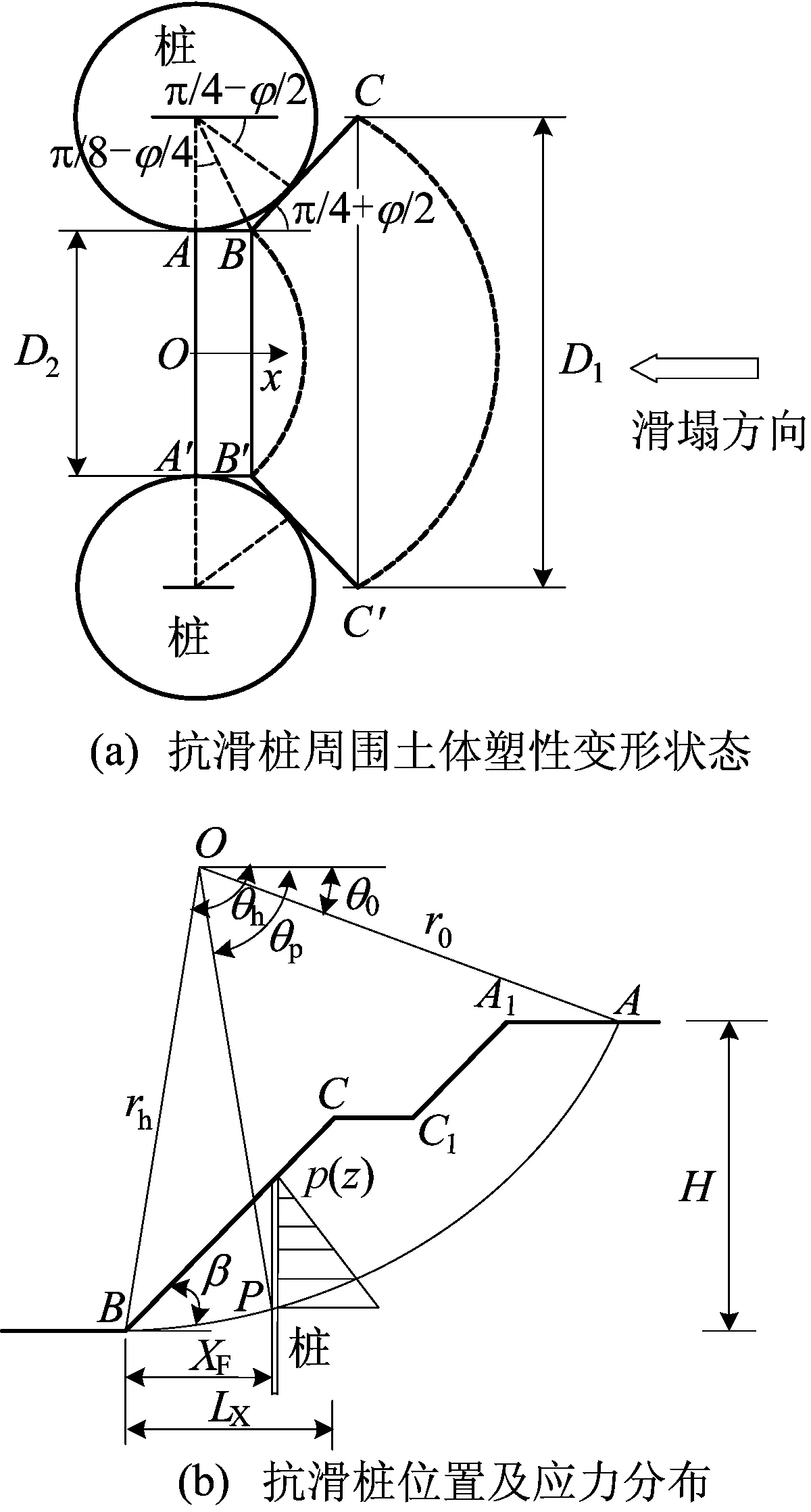
图3 抗滑桩应力分析

本文计算抗滑桩与土体作用力采用Ito模型[18],计算图式如图3a所示。假定:① 当土层变形时,沿ABC和A′B′C′ 2个滑动面滑动;② 抗滑桩为刚性;③ 只有抗滑桩周围ABCC′B′A′的土体处于塑性平衡状态,且服从Mohr-Coulomb准则;④ 在深度方向上,土层处于平面应力状态;⑤ 在考虑塑性区ABCC′B′A′的应力分量时,作用在ABC(A′B′C′)面上的应力忽略不计。抗滑桩侧向力p(z)的计算公式为:

(33)

Nφ=tan(π/4+φ/2),

其中:D1为2个相邻抗滑桩的中心距;D2为相邻2个抗滑桩边缘最小距离;dp为抗滑桩直径,dp=D1-D2;rz为桩上任一点到旋转中心O的距离,z为抗滑桩在土体内任一点的埋深。

根据(33)式,桩侧有效土压力作用在水平方向上,并以三角形形式分布,如图3b所示。

抗滑桩的内能耗散由抗滑桩对“牛角形块体”的做功功率Dpsoil和抗滑桩作用下插入块体的内能耗散功率Dpsoilb组成,其计算公式分别为：

(34)

(35)

其中:h为抗滑桩的埋深;x(z)为抗滑桩深度为z处边坡破坏土体宽度的1/2;l(z)为桩上任一点到旋转中心处的竖直距离。

x(z)、l(z)表达式分别为:

(36)

l(z)=rhsinθh-XFtanβ1+z

(37)

XF=rpcosθp-rhcosθh

(38)

(39)

其中:Re=(re-re′)/2,rme=(re+re′)/2,re为桩上任一点与O点连线的长度,re′为桩上任一点与O点连线和牛角破坏模型的交点至O点距离;l为桩上任一点到旋转轴的垂直距离;rp为桩与破坏面的交点P和O点连线的长度;θe为桩上任一点与O点连线的倾角。

抗滑桩引起的总内能耗散功率为:

Dp=Dpsoil+Dpsoilb

(40)

总外力功率为:

D=Ds+Dp

(41)

1.3 安全系数求解

在实际工程中,与边坡临界高度Hcr相比,工程人员更在意的往往是边坡的安全系数Fs,其计算公式为:

(42)

其中,cm、φm为破坏块体达到平衡状态时的土体强度参数。

Fs通过二分方法求得,其过程如下:

(1) 给定边坡安全系数Fs的1对初始值Fs1、Fs2(Fs1≤Fs2),则边坡安全系数搜索初值为Fs=(Fs1+Fs2)/2。

(2) 对土体强度参数c、φ进行折减,以θ0、θh、r0′/r0和插入块体的相对宽度b/H为自变量搜索，求得min|W-D|,若min|W-D|=0,即W=D时,则Fs即为边坡安全系数的上限解,此时Fs2=Fs。

(3) 否则,Fs1=Fs,重复上述过程;直至Fs2-Fs1小于设定的误差值ΔFs。

2 影响因素敏感性分析

对于抗滑桩加固边坡,影响其稳定的因素主要有以下3类:① 边坡强度参数与几何参数;② 抗滑桩设计参数;③ 外部因素，如地震荷载等。

对于边坡强度参数与几何参数,主要考虑岩土材料的黏聚力c、内摩擦角φ,边坡倾角β1、β2，边坡宽高比B0/H及边坡平台宽度L2等因素。对于抗滑桩设计参数,主要考虑抗滑桩的位置XF/LX、抗滑桩的分布参数D1/dp等。对于地震荷载,则主要考虑水平地震力系数kh。为了简化分析,本文只选择上述8个因素进行敏感性分析。

针对以上8个因素,假设各因素间无交互作用,对边坡进行正交实验设计。参数取值范围按照一般工程边坡确定,并将其概化为高、中、低3个水平。对于三水平八因素正交实验,选用L27(313)正交表,其最少实验次数为27次,设计方案见表1所列。表1中,边坡倾角βj(j=1,2)的3个水平分别为:Ⅰ水平下,β1=60°,β2=50°;Ⅱ水平下,β1=50°,β2=40°;Ⅲ水平下,β1=40°,β2=30°。

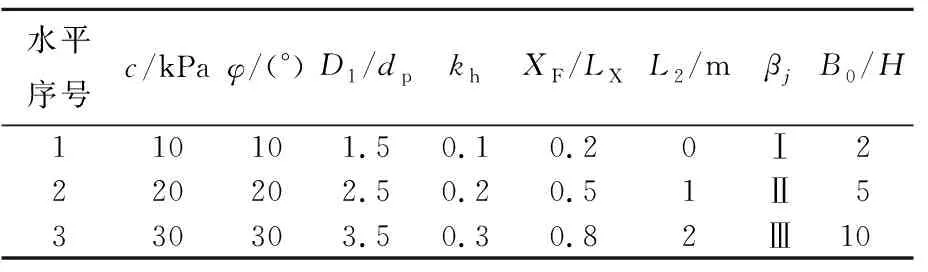
表1 三水平八因素L27(313)正交设计方案

为了减少由于水平次序引起的系统误差,各个因素水平的次序应随机排列,按抽签方式确定的因素水平次序见表2所列。计算时取γ=19.63 kN/m3,α1=α2=1/2,H=10 m。

各参数的极差分析见表3所列。通过极差分析可得到各因素的敏感性从大到小依次为:黏聚力c、内摩擦角φ、边坡倾角βj、水平地震力系数kh、抗滑桩位置XF/LX、抗滑桩结构参数D1/dp、边坡宽高比B0/H、边坡平台宽度L2。通过排序分析可知,c、φ对边坡稳定性影响的敏感性最大,而L2的敏感性较小。边坡的安全系数越大,稳定性就越好,从而得到最优组合方案,即(c)3(φ)3(D1/dp)1(kh)1(XF/LX)3(L2)2(βj)3(B0/H)1,括号外的下标表示各因素的水平。

各因素趋势分析如图4所示。由图4可知,安全系数Fs随着c、φ、XF/LX和L2增加而增大,随着βj、D1/dp、kh和B0/H增大而减小。

通过以上分析可得到如下结论:

(1)c、φ对边坡稳定性影响的敏感性最大,对于土体c和φ较小的边坡,工程上需密切关注其稳定性问题。

(2) 对边坡几何参数而言,边坡倾角βj对边坡稳定性的影响最大,平台宽度L2对边坡稳定性的敏感性最小。在工程条件允许情况下，应优先减小边坡倾角以提高稳定性。

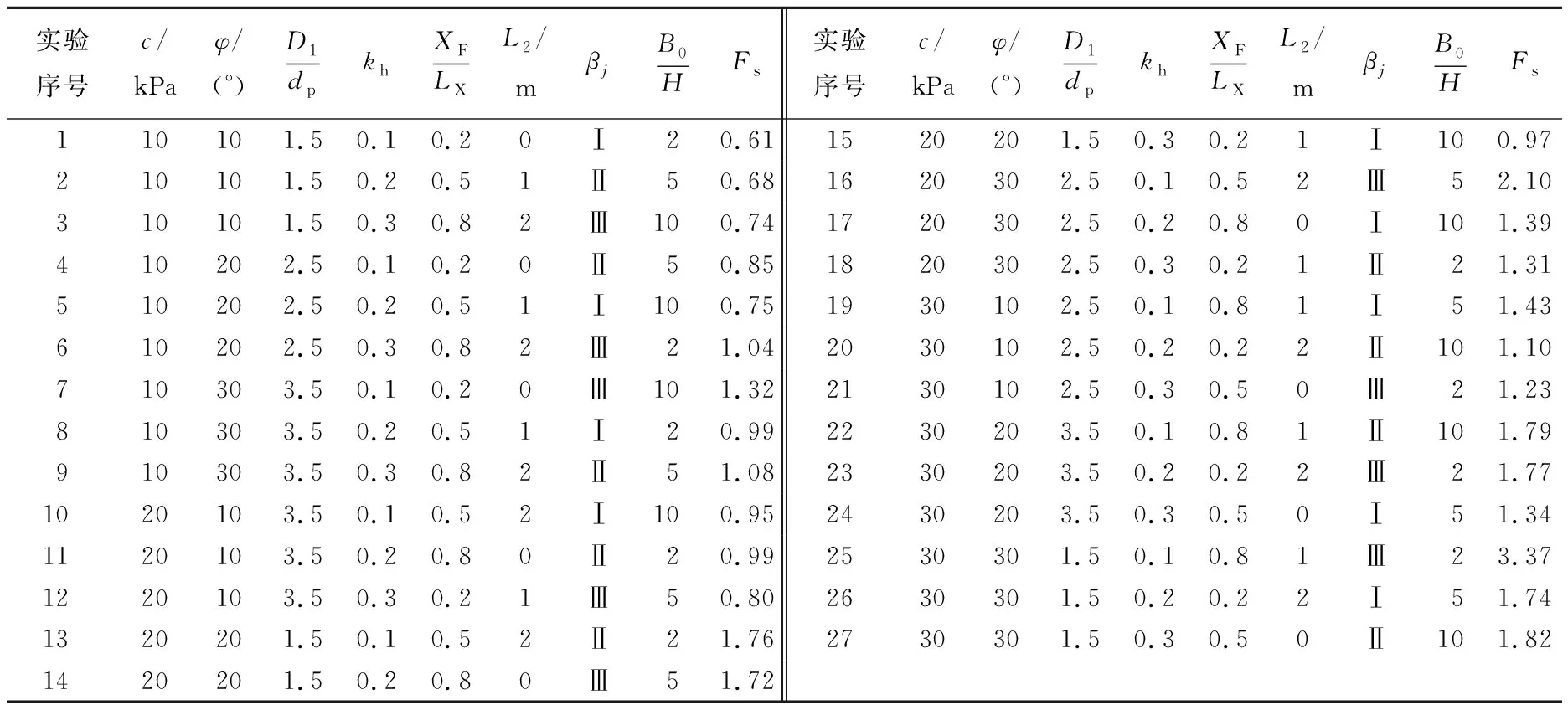
表2 正交实验结果

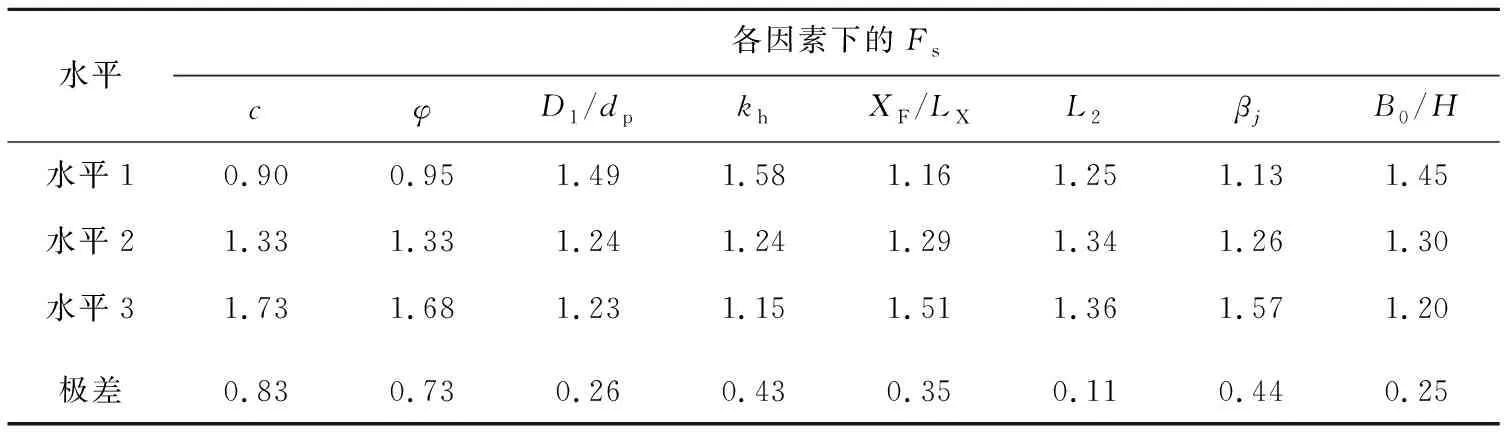
表3 各因素对边坡安全系数Fs影响程度极差分析

图4 各因素趋势分析

(3) 抗滑桩对边坡稳定性影响的敏感性较大,位置参数XF/LX的敏感性高于结构参数D1/dp。因此,工程上应优先考虑抗滑桩的布设位置。

(4) 水平地震力系数kh的敏感性影响介于边坡倾角和抗滑桩之间,对边坡稳定性的影响较为显著,在边坡设计时要充分考虑。

3 设计参数对边坡安全系数的影响

地震条件下，各影响参数对抗滑桩加固边坡的三维稳定性影响如图5所示。图5中,B0/H取值为1、2、5、10,β1、β2取值为30°～60°,kh取值为0～0.20,XF/LX取值为0～1.0,L2取值为0～2.0 m,D1/dp取值为1.5～3.5。其他相关参数取值分别为:c=23.94 kPa,φ=10°,γ=19.63 kN/m3,H=10 m,α1=α2=1/2。

由图5a、图5b可知,边坡倾角β1、β2对边坡稳定性有显著影响。Fs随着β1、β2增大而减小,基本呈线性变化,随着B0/H增大,该趋势的非线性特征略有增加。在本文工况下,边坡倾角β1、β2对安全系数Fs的影响基本相同。

由图5c可知，地震力对边坡三维稳定性有显著影响，Fs随着kh增加而迅速下降，且其下降规律基本为线性变化。

由图5d可知，设置平台有利于提高边坡稳定性。当B0/H=1，不设平台与设置2.0 m宽平台相比，Fs由1.57提高至1.72；增大L2可以提升边坡的稳定性，但效果并不显著。工程上决定是否设置平台及确定平台宽度，可以从施工便捷性等多方面综合考虑。

由图5e、图5f可知,抗滑桩能显著提升边坡的稳定性能。在B0/H=10,D1/dp=1.5的情况下,XF/LX=1.0时抗滑桩的加固效果最好。当抗滑桩布置在下级边坡时,Fs随着XF/LX增加而增大;同时,Fs随着D1/dp增加而减小。由此可知,若抗滑桩的布置范围限定在台阶平面及以下时,布设位置越高,带来的加固效果越显著。

由图5可知，边坡宽高比B0/H对边坡稳定性的影响呈非线性变化,Fs随B0/H减小而迅速增大,当B0/H≤5时,边坡的三维特性表现得较显著。因此,在边坡加固设计时要充分考虑B0/H的影响。

从因素敏感性分析及设计参数分析可知,在地震作用下,抗滑桩的位置对边坡稳定性的影响显著。利用上述边坡算例,改变抗滑桩在边坡中的位置及相应参数,使XF/LX在0～1.0之间变化,得到Fs随XF/LX变化曲线,如图6所示。

图5 不同参数取值对三维边坡稳定性的影响

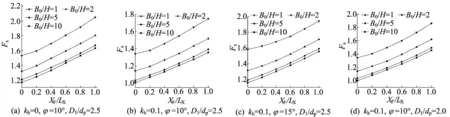
图6 不同抗滑桩位置时三维边坡稳定性的变化规律

由图6可知:Fs随着抗滑桩位置参数XF/LX的增加而增大,且其增幅高达40%;在改变其他参数时,Fs始终随着XF/LX增加而增大,并在XF/LX=1.0时达到最大值,此时边坡处于最稳定状态,说明在该处边坡加固效果最好,则XF/LX=1.0处即抗滑桩布置的最优位置。

4 结 论

(1) 由边坡的敏感性分析可知,边坡的强度参数c、φ和边坡倾角对边坡的稳定性影响最大,抗滑桩参数XF/LX、D1/dp对边坡稳定性也有较大的影响;水平地震力系数kh对边坡稳定性的影响介于边坡倾角与抗滑桩之间;而边坡宽高比B0/H与平台宽度L2对边坡稳定性的影响较小。

(2) 从边坡几何参数看,边坡倾角对边坡稳定性的影响最大,在边坡稳定性设计时应优先考虑；结合影响因素参数分析,β1、β2对边坡安全系数Fs的影响基本呈线性变化,且影响程度大致相同。

(3) 抗滑桩对台阶边坡的三维稳定性影响较为显著。结合参数分析可知,抗滑桩的位置在XF/LX=1.0时加固效果最优,因此抗滑桩应布置在相对较高的位置(最好在平台上)。虽然减小D1/dp能取得加固效益,但其对安全系数的影响呈非线性减小,选择合理的D1/dp能取得较好的加固效益。

(4) 边坡宽高比B0/H对其稳定性的影响呈非线性变化,Fs随B0/H减小而迅速增大,特别是当B0/H≤5时,边坡的三维特性表现得较为显著。因此,在边坡加固设计时要充分考虑B0/H的影响。

(5) 平台宽度L2对两级台阶边坡的三维稳定性影响较小,但一定宽度的平台能为抗滑桩的施工提供方便,因此在工程中应结合实际情况合理选择平台宽度。