基于基波正序分量谐振的锁相策略

李 锐，郑中祥，魏 华，吴浩伟，陈 涛

基于基波正序分量谐振的锁相策略

李 锐，郑中祥，魏 华，吴浩伟，陈 涛

(武汉第二船舶设计研究所，武汉 430205）

提出了一种基于电网正序分量谐振的同步旋转坐标系下的锁相方案。该方案首先将电网电压转换到同步旋转坐标系下，对电网电压中正序分量进行谐振预处理，将电网电压正序分量幅值放大，然后再进行锁相控制。这个预处理过程的作用等效为陷波器叠加带通滤波器的效果，可以有效的抑制电网电压谐波的影响，同时兼顾系统动态响应速度。最后通过与相位超前补偿陷波器方案对比，验证了该方案动稳态控制效果的优势。

锁相环 电压不平衡 谐振 谐波

0 引言

锁相技术是实现逆变器成功并网的关键技术之一，是逆变器实现并网运行的前提。如何高速准确的提取电网电压的相位，有效消除电网不平衡以及电网电压谐波等非理想因素对锁相结果的影响，一直是锁相技术研究的重点。

其中三相逆变系统在同步旋转DQ轴坐标系下的锁相技术，由于理论含义清晰、实现简单、锁相速度较快而获得了迅速的发展[1-3]。单相逆变系统也可以通过虚拟三相来应用锁相技术[4,5]。

电网电压不平衡和电网谐波会对锁相准确性带来很大的影响。电网电压不平衡会导致锁相结果中出现相应的2次纹波问题。电网电压中的谐波分量通过DQ变换后，正序谐波分量在Q轴上会降次，而负序谐波分量在Q轴上会升次，从而导致锁相结果中出现相应的谐波。许多学者针对电网电压不平衡和谐波污染的问题，提出了一系列的改进方案。

有的学者提出了正负序分离锁相的方案[6-9]，来解耦正序与负序分量，然而这种方案数学解析复杂。有的学者采用低通滤波器的方案[1-4]，将2次纹波和多次谐波滤除，然后再进行比例积分控制，然而低通滤波器需要设置很低的截止频率，使系统动态特性变差。另外有学者则提出了用多个陷波器来代替低通滤波器[10-14]，可以对电网电压中常见的谐波分量进行陷波处理，这种方案可以改善系统动态特性，且能有效滤除2次纹波和主要谐波分量，然而陷波器会降低系统稳定性，且电网频率发生偏移时，陷波器效果会下降。针对常规陷波器的问题，文献[14]提出了一种带有相位超前校正的陷波器，这种陷波器在陷波频率点相位是超前跳变，从而提高系统的稳定性，该文献还对陷波频率进行了自适应调节，从而适应电网电压频率的变化。然而陷波器方案在多个陷波器级联后动态特性均会显著变差。基于陷波器的问题，很多学者相继提出了一些现代数字滤波器来抑制纹波影响[15,16]，同时提高系统的锁相速度，如FIR滤波器、梳状滤波器等。然而这些滤波器实现相对复杂，滤波效果受到控制频率影响。

本文提出了提出了一种基于基波谐振的锁相方案，有效的抑制锁相环节带来的谐波分量。该方案通过对采样的电网电压进行预处理，将电网电压进行负序DQ变换，然后经过100 Hz谐振放大，最后进行DQ反变换后送入锁相环输入，这个预处理环节等效为一个陷波器和一个带通滤波器的效果，陷波器主要消除负序分量，而带通滤波器只通过50 Hz正序基波分量，从而达到消除谐波的作用。最后通过与一种改进的陷波器锁相方案进行仿真对比，验证了该锁相控制方案的有效性和先进性。

1 锁相环建模分析型

综合考虑电网相位扰动以及电网背景谐波扰动后的锁相环控制模型如图1所示。

图1 锁相环小信号模型

观察图1所示的模型可以发现，考虑电网电压谐波扰动的模型中控制环路有两个输入：电网电压中的相位扰动和电网电压的幅值扰动。常规锁相环线性模型分析系统性能时，建立的是锁相环输出对电网电压相位扰动的闭环传函，这种模型可以分析锁相控制器对电网相位变化的动态响应能力，但并不能很好的反应锁相控制器对谐波抑制的能力；基于本文提出的线性化模型，建立锁相环输出对电网电压幅值扰动的闭环传函，可以分析锁相环对电网电压中谐波扰动的抑制能力。分别建立输出相位对参考相位和以及电网谐波扰动的闭环传函可以得到：

式中G()是PI控制器传函，可以看到锁相环的控制特性与PI参数以及参与锁相计算的电网电压的峰值都直接相关。

图2为在表1所示参数，不同电网电压幅值的两个闭环传函的波特图。从传函图中可以发现，当PI参数一定时，电网峰值V越高，G()的闭环带宽越大，那么对电网电压相位突变的响应速度也越快。同时V越高，G()低频段的幅值增益也越低，那么对电网电压背景谐波的衰减系数也越大，V=100时100 Hz处增益为-40 dB，V=300时增益降低至-50 dB。因此，系统控制参数确定后，参与锁相计算的电网电压幅值会直接影响锁相控制的动稳态性能。电网电压幅值越高，动态响应速度越快且谐波抑制能力越强。

图2 闭环传函波特图

表1 锁相环参数.

2 锁相方法设计

从上述两个闭环传函可以发现，电网电压幅值越大，系统闭环带宽越宽，对低频谐波的抑制能力同时也越强，因此增加电网电压幅值可以有效的抑制谐波，同时兼顾系统动态特性。基于这样一种思路，本文提出了一种将电网电压中基波正序分量进行谐振预处理的锁相方案，后面简称为R-PLL方案，具体方案示意图如图3所示。将三相电网电压以-50 Hz的频率进行DQ变换，此时电压中基波正序分量变为100 Hz，而基波负序分量变为直流量；再通过一个100 Hz的准谐振控制器，将基波量放大，而负序量因为变换为了直流量，经过谐振控制器后则会衰减至零；其他次谐波经过谐振控制器后也会相应的衰减，之后再经过DQ反变换变为ABC三相电压。经过这样一个预处理的过程，就可以有效的将电网电压中正序分量峰值放大，同时又抑制电网电压中其他分量的干扰，其中谐振控制器的表达式如下：

图4所示为不同ω下发生相位突变时的动态响应，可以看到随着ω增加，系统的调节时间逐渐减少，而超调量则会增加。图5所示为不同ω下发生负序分量突变时的动态响应，可以看到较小时即阻尼较小时，会出现较大和较长时间的振荡；随着ω增大，振荡减小调节时间变短，但是超调量会增加；当ω继续增大至阻尼比大于1之后，振荡消失，但是调节时间和超调量都会增加。图6所示为谐振控制器的波特图，从图6中可以看到ω增大对低频谐波的抑制能力会降低，但是对于负序分量的抑制能力始终是100%。

图4 相位突变动态响应

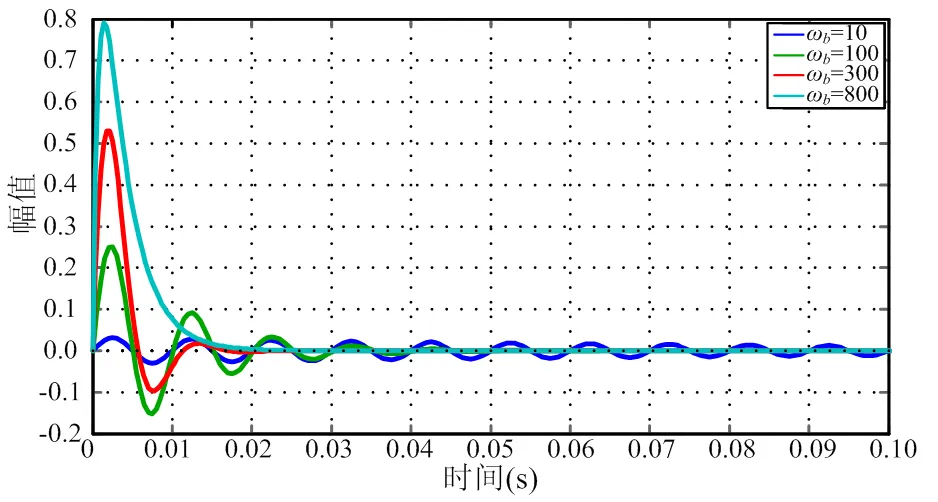
图5 负序分量突变动态响应

图6 R(s)波特图

从这里可以看出R-PLL方案的特点：1）相比较传统锁相方案可以有效的消除负序分量的影响；2）在消除负序分量的基础上可以有效的抑制各次谐波分量；3）通过ω参数的调节，可以兼顾动态特性和低频谐波抑制能力。

3 仿真对比

3.1 不同阻尼参数下R-PLL控制效果对比

锁相控制器按照表1所示进行设计，按照图3的锁相控制方案搭建仿真模型。图7中(a)～(b)所示分别为ω等于10和300参数下的相位突变90°时的动态响应，波形具体为锁相相位结果与实际电网电压相位之间的误差。可以看到ω等于300时对相位突变的动态响应速度远优于ω等于10。(c)～(d)所示分别为两种参数下电网电压中负序分量发生突变的动态响应。同样可以发现ω等于300时动态响应更优。(e)～(f)所示分别为电网中存在20%的7次谐波时，两种参数下的稳态控制效果，波形具体为锁相环节中的v。可以看到ω等于10参数下谐波含量非常小，要优于ω等于300参数下的控制效果。但是即使ω等于300，谐波的扰动依然被削弱到非常小，相位中波动幅值不超过0.05。仿真结果验证了之前的理论分析，在设计谐振环节时，需要折中考虑ω参数的选取，在保证一定动态响应速度的条件下尽可能增加其谐波抑制能力。

3.2 R-PLL与N-PLL控制效果对比

将R-PLL与文献[14]所述的改进型陷波器方案（N-PLL）的控制效果进行对比，其中陷波器方案的陷波频率点也设计为对负序分量陷波。这种改进型陷波器在传统陷波器基础上增加了一个相位超前补偿，从而可以改善传统陷波器引入的相位滞后对锁相环稳定性的不利影响。但是这种陷波器同时增加了一个谐振峰，虽然可以设计谐振峰为间谐波点，但仍然会放大电网中的一些谐波分量。总体来说，该改进型陷波器动稳态特性均要优于传统陷波器，本文所提方案直接与此改进型陷波器进行比较，验证本文所提锁相方案的优势。

图8为R-PLL与N-PLL的控制效果对比。(a)所示为两种方案在相位突变90°时的动态效果，其中蓝色为基波谐振方案，绿色为陷波器方案。可以看到两种方案都能迅速在相位突变后收敛到新的相位附近，然而陷波器方案会有较长时间的相位的波动，在80 ms之后相位波动幅值才缩小到1°以内；而基波谐振方案可以迅速的收敛，在10 ms之后相位波动幅值已经小于1°。(b)所示为两种方案在负序分量突变100%时的动态效果，其中蓝色为基波谐振方案，绿色为陷波器方案。可以看到基波谐振方案在1个周期内就迅速收敛，相位振荡值很小，最大相位波动仅为14°；而陷波器方案相位剧烈振荡，150 ms之后才逐渐收敛，最大相位波动达到70°。(c)所示为两种方案在100%负序分量和20%的7次谐波分量条件下，锁相控制器的稳态波形。可以看到陷波器由于只有陷波效果，没有低通滤波效果，导致谐波含量很大，从THD分析可以看到谐波含量达到25%以上，且7次谐波衍生出了大量新的谐波分量。而基波谐振方案等效在陷波器的基础上增加了对其他次谐波的滤波效果，使的相位中的谐波分量得到了有效抑制，谐波含量仅为3.33%。仿真结果验证了基波谐振锁相控制器的优势。

4 结论

本文提出了一种基波谐振锁相环方案。该方案通过对电网电压进行谐振预处理，将电网电压幅值放大，其作用可以等效为一个陷波器叠加一个带通滤波器的效果，可以有效的抑制电网电压谐波的影响，同时兼顾系统动态响应速度。最后通过与陷波器方案对比，验证了该方案在相位突变、负序分量突变以及存在大量背景谐波和负序分量下的动稳态控制效果上的优势。

[1] Nicastri, A., Nagliero, A. Comparison and evaluation of the PLL techniques for the design of the grid-connected inverter systems. in: Proc. of Industrial Electronics (ISIE), 2010 IEEE International Symposium on. Bari. 2010. 3865-3870.

[2] Santos Filho, R. M., Seixas, P. F., Cortizo, P. C., et al. Comparison of three single-phase pll algorithms for ups applications. industrial electronics, IEEE Transactions on, 2008, 55(8): 2923-2932.

[3] Meersman, B., De Kooning, J., Vandoorn, T., et al. Overview of PLL methods for distributed generation units. in: Proc. of Universities Power Engineering Conference (UPEC), 2010 45th International. Cardiff, Wales. 2010. 1-6.

[4] Ferreira, R. J., Araujo, R. E., Pecas Lopes, J. A. A comparative analysis and implementation of various PLL techniques applied to single-phase grids. in: Proc. of Energetics (IYCE), Proceedings of the 2011 3rd International Youth Conference on. Leiria. 2011. 1-8.

[5] Youngjong, K., Kiwoo, P., Kyo-Beum, L., et al. A new PLL system using full order observer and PLL system modeling in a single phase grid-connected inverter. in: Proc. of Power Electronics and ECCE Asia (ICPE & ECCE), 2011 IEEE 8th International Conference on. Jeju. 2011. 803-808.

[6] Rodriguez, P., Pou, J., Bergas, J., et al. Decoupled double synchronous reference frame pll for power converters control. power electronics, IEEE Transactions on, 2007, 22(2): 584-592.

[7] Rodriguez, P., Teodorescu, R., Candela, I., et al. New positive sequence voltage detector for grid synchronization of power converters under faulty grid conditions. in: Proc. of Power Electronics Specialists Conference, 2006. PESC '06. 37th IEEE. 2006. 1-7.

[8] 邓哲, 周峰武, 林辉品, 等. 电网故障时基于双输SOGI-FLL 的改进电网快速同步方法[J]. 电工技术学报, 2013, 28(12): 32-43．

[9] 陈东明, 陈明亮, 谢桢, 等. 基于改进滤波及正负序分离法的锁相环[J]. 电网技术, 2016, 40(3): 931-937．

[10] Kyoung-Jun, L., Jong-Pil, L., Dongsul, S., et al. A Novel grid synchronization pll method based on adaptive low-pass notch filter for grid-connected pcs. industrial electronics, IEEE Transactions on, 2014, 61(1): 292-301.

[11] Karimi-Ghartemani, M., Khajehoddin, S. A., Jain, P. K., et al. Addressing DC Component in PLL and Notch Filter Algorithms. Power Electronics, IEEE Transactions on, 2012, 27(1): 78-86.

[12] Bellini, A., Bifaretti, S. Performances of a PLL based digital filter for double-conversion UPS. in: Proc. of Power Electronics and Motion Control Conference, 2008. EPE-PEMC 2008. 13th. Poznan. 2008. 490-497.

[13] Mojiri, M., Karimi-Ghartemani, M., Bakhshai, A. Processing of harmonics and interharmonics using an adaptive notch filter. power delivery, IEEE Transactions on, 2010, 25(2): 534-542.

[14] Freijedo, F. D., Yepes, A. G., Lo, et al. Three-Phase PLLs with fast postfault retracking and steady-state rejection of voltage unbalance and harmonics by means of lead compensation. power electronics, IEEE Transactions on, 2011, 26(1): 85-97.

[15] Carugati, I., Maestri, S., Donato, P. G., et al. Variable sampling period filter pll for distorted three-phase systems. power electronics, IEEE Transactions on, 2012, 27(1): 321-330.

[16] Robles, E., Ceballos, S., Pou, J., et al. Variable-Frequency Grid-Sequence Detector Based on a Quasi-Ideal Low-Pass Filter Stage and a Phase-Locked Loop. Power Electronics, IEEE Transactions on, 2010, 25(10): 2552-2563.

A PLL algorithm based on the resonance of the positive sequence component of grid voltage

Li Rui, Zheng Zhongxiang, Wei Hua,Wu Haowei, Chen Tao

(Wuhan Second Ship Design and Research Institute, Wuhan 430205, Hubei, China）

TM761

A

1003-4862（2022）09-0004-06

2022-02-10

海洋核动力平台技术、装备研制及示范应用（2017YFC0307800）

李锐（1987-），男，博士，研究方向：船舶综合电力系统。E-mail: learoylr@163.com