近极槽水下电机径向和切向力波振动分析及抑制
李 畅,夏加宽,张津铭,赵圣杰
近极槽水下电机径向和切向力波振动分析及抑制
李 畅,夏加宽,张津铭,赵圣杰
(沈阳工业大学,电气工程,电气传动研究所)
本文首先分析了近极槽水下电机径向和切向的电磁力波的表达式,并结合有限元方法和傅里叶分解,分析了电机的径向力和切向力对电机振动及形变的影响,得出了径向力和切向力对电机振动形变作用不同的结论,并通过改变电机的极弧系数来抑制电机的振动。
电机振动 径向切向力波 极弧系数
0 引言
近极槽永磁电机通过极槽数相近的结构设计方法,解决了永磁电机极数多和槽数有限的矛盾,满足了电机高效率、高转矩密度的要求。它被广泛应用于潜艇推进、船舶动力等领域[1-3]。这些场合一般对设备的振动噪声有着较高的要求,而电机是其设备主要的振动噪声来源,所以近年来近极槽电机振动噪声的研究得到了广泛的关注。
由于切向力波的时域幅值一般小于径向力波的时域幅值,所以人们普遍认为电机的振动只要是由径向力波引起的,在计算电机振动效应时,一般忽略切向力波[4]。而电磁力波谐波分量是电机振动的主要因素,时域的大小通常只影响低阶次的谐波[5],近极槽电机中存在大量的电枢磁动势谐波,这些谐波会导致近极槽电机的切向力波大于整数槽的切向力波[6]。文献[7-8]分析了径向和切向力波的单位力波振动响应,证明电机振动对切向力波的敏感度比对径向力波还要大,以此说明切向力波对近极槽电机振动噪声的影响不容忽略。
文献[9]提出了近极槽电机由于较大的齿顶漏抗产生了六次纹波转矩引起的转矩脉动,但并未进一步分析电机的振动特性。文献[10]推导了径向力波的解析表达,分析了表贴式近极槽电机由径向力波所引起的振动噪声效应,但并未分析切向力波对电机振动噪声的影响。
所以本文以一台22极24槽分数槽电机为例,通过对比电机径向和切向力波对振动作用效果,分析了电机径向切向力波产生振动的机理,并利用调整极弧系数减小径向切向力波产生的振动效应。
1 电机模型及参数
本文研究的水下推进用永磁同步电机如图1所示,该电机是一台10 kW、22极24槽表贴式永磁同步电机,具体参数如表1所示:

图1 水下推进电机示意图

表1 永磁同步推进电机主要参数
2 电机径向和切向力波
2.1 空载工况下的径向切向力波
将空载径向气隙磁密的表达式代入,得到空载径向力波:

其大小与径向磁密各分量幅值之间的乘积有关。式中空间阶数和时间次数分别为
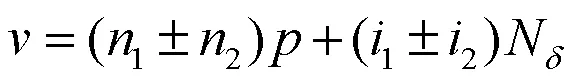

切向力波表达式:

空载径向和切向电磁力波所包含的谐波含量完全相同,两者的区别仅仅是幅值和相位的差异,径向和切向电磁力波的空间阶数均可表示为:

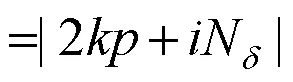
时间次数则均可表示为:
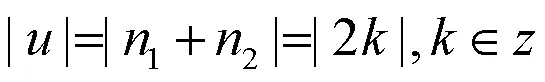
2.2 负载工况下的径向切向力波
负载时的径向力波主要分为三部分:
1)空载磁场内部谐波的相互作用

2)电枢反应磁场内部谐波的相互作用:
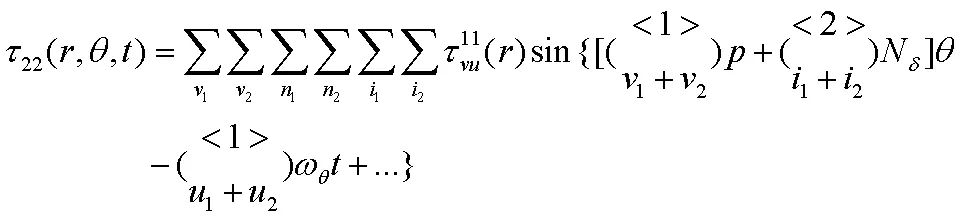
3)空载磁场与电枢反应磁场谐波之间的相互:

同理,负载时的切向力波主要分为三部分:空载磁场内部谐波的相互作用、电枢反应磁场内部谐波的相互作用、空载磁场与电枢反应磁场谐波之间的相互作用。

图3 径向电磁力密一维傅里叶分解
图2为初始时刻的气隙电磁力密度波形,切向电磁力密度整体幅值要小于径向电磁力密度。对电磁力波进行一维傅里叶分解,可以得出: 不论径向力波还是切向力波,他们产生电磁力的频率均为基波电流频率f的偶数倍。且基波磁场产生的频率为2f的电磁力波幅值最大,是电机电磁振动最主要的激振源。

图4 切向电磁力密一维傅里叶分解
通过电机的时域电磁力密度进行二维傅里叶变换可得到,无论是径向力波还是切向力波,在不考虑0阶力波的情况下,忽略幅值较小的电磁力,空间阶数为2时间次数为2、空间阶数为4时间次数为4为主要的电磁力波。近一步分析表的力波分量可知电磁力波的空间和时间谐波成分几乎完全相同。
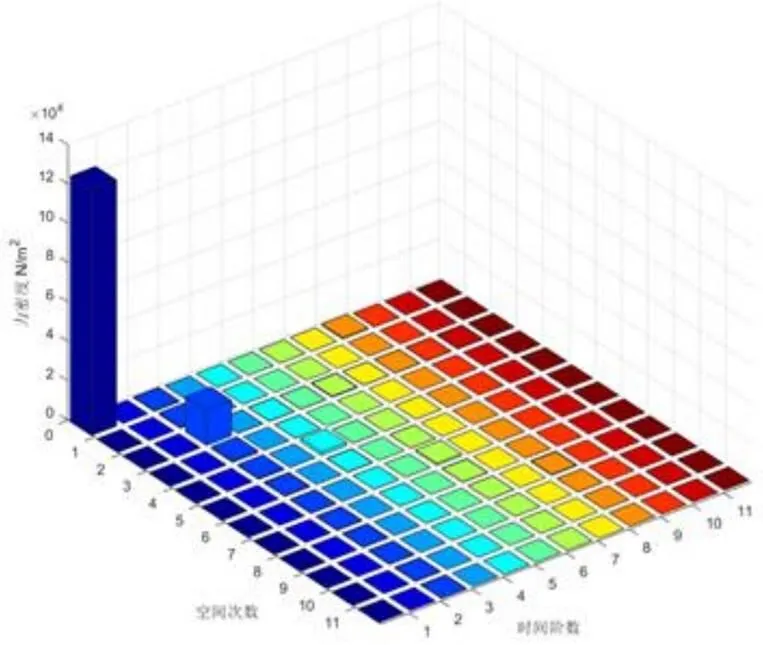
图5 径向力波二维傅里叶分解

图6 切向力波二维傅里叶分解

表2 径向力波阶次分析

表3 切向电磁力波分析
3 径向和切向电磁力波引起振动的机理
电机机壳近似圆台形状,电机正反两面的半径大小不同。为了研究力波引起电机振动的机理,分别在定子齿上施加径向力波和切向力波得到电机的形变云图。可以得到电机的径向力波和切向力波所形成的形变大致趋势相同,但是程度不同。

图7 电机机壳示意图
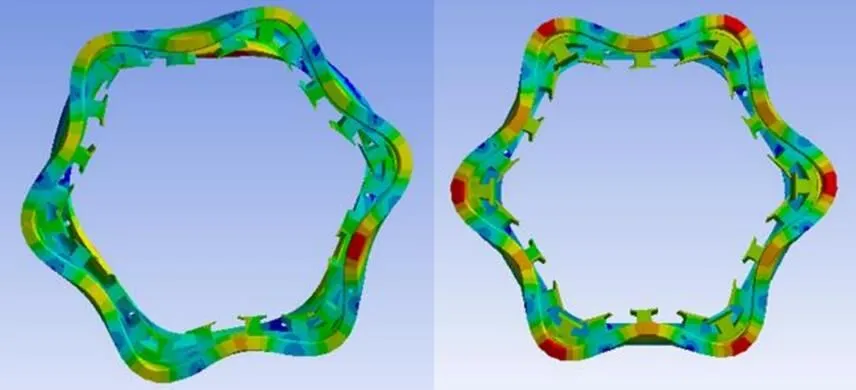
图8 切向力波(左)和径向力波分(右)分别作用的电机形变云图正面

图9 切向力波(左)和径向力波(右)分别作用的电机形变云图反面
电机切向力和电机径向力一样对电机起着明显的形变作用,但是两者的作用效果不相同,对于电机半径较大端的机壳形变,径向力的作用效果更为明显,但是对于电机机壳半径较小和机壳端部的环形面来说,反而是切向力的作用效果更加显。
径向力波和切向力波作用于定子齿上,并传递给电机的定子轭部和机壳,从而引起电机发生振动而导致形变。由于计算振动过程中将齿部与轭部分割,分离出的齿部横截面积较小,可忽略定子齿形变。所以在电磁力波作用的过程中,我们一般考虑机壳和定子轭的形变,而认为定子齿像一个刚体一样,几乎不发生形变。

图10 切向力作用在定子齿上的示意图
在施加切向力时,定子齿可以和作用在齿冠上的切向力进行配合,定子齿就像杠杆一样,在切向力波的作用下给定子轭施加弯曲力矩,从而导致轭部产生弯曲变形。且无论在机壳半径大还是小的部分,所形成的形变都较为明显。
4 改变极弧系数抑制电磁力波
电机的电磁力波主要分为三部分:第一部分由空载磁场内部谐波的相互作用引起,第二部分则是由电枢反应磁场内部谐波的相互作用引起,第三部分是两者相互作用所引起的。而改变极弧系数可以改变电磁力波谐波的分布,通过调整电机的极弧系数,就可以有效的削弱电磁力波。过小的极弧系数会使电机的转矩下降,所以本文选择0.5至1范围步长为0.05的极弧系数进行仿真模拟,从而得到极弧系数的最优区间。
利用有限元软件进行电机的振动分析,可得出极弧系数与各阶次倍频加速度的关系。图11和图12可以看出:随着极弧系数的减小,二倍频加速度和四倍频加速度普遍呈下降的趋势。但是在极弧系数为0.85时,电机的振动加速度略有减小。所以适当地减小极弧系数可以抑制电机的径向和切向振动。

图11 极弧系数与二倍频加速度图

图12 极弧系数与四倍频加速度图

图13 极弧系数与平均转矩关系图
利用有限元软件进行电机的电磁分析,可得出极弧系数与转矩的关系图,如图13 。由此可知极弧系数越大,所对应的平均转矩越大,本文所采用的水下电机要求转矩≥100 Nm,所以当极弧系数≥0.75时符合电机所转矩要求。
为了满足电机转矩的要求,极弧应选取大于等于0.75的值,为了能够有效的抑制电机的振动效应,所以选择电机的极弧系数为0.85。此时电机的二倍频振动加速度为106.3m/s2,较原来电机的二倍频振动加速度120.7m/s2少了13.5%。此时电机的四倍频速度为0.579m/s2,较原来电机的二倍频速度4.56 m/s2少了87.3%。综上所述,当极弧系数为0.85时能够满足电机的转矩要求同时也降低了电机的振动。
5 结论
本文以一台22极24槽电机为例,主要分析了近极槽水下电机的径向和切向振动,并通过改变极弧系数的方法抑制了电机的振动。可得出如下结论:
1)近极槽电机中,切向力对振动的影响不容忽略,并且切向力主要影响电机机壳半径较小和机壳端部的环形面的形变。
2)随着极弧系数的增加,电机振动也随之减小,但于此同时,电机的转矩也随之较小。
3)当极弧系数为0.85时,能够保证在满足电机转矩的同时,能够有效的降低振动,二倍频加速度减少了13.5%,四倍频加速度减小了87.3%。
[1] 李廷斌, 杨峥, 蔡昌泽, 等. 高频脉振注入法在电力推进中的应用研究[J]. 船电技术, 2020, 40(10): 49-52.
[2] Gerada C, Bradley K, Whitley C, et al. High torque density PM machines for high performance operation[C]. The 33rd Annual Conference of the IEEE on Industrial Electronics Society, 2007: 210-215.
[3] Refaie El A M. Fractional-slot concentrated-windings synchronous permanent magnet machines: opportunities and challenges[J]. IEEE Transactions on Industrial lectronics, 2010, 57(1): 107-121
[4] 陈益广, 韩柏然, 沈勇环, 魏娟, 郭喜彬. 永磁同步推进电机电磁振动分析[J]. 电工技术学报, 2017, 32(23): 16-22.
[5] 兰华. 永磁同步电机的电磁力波与电磁振动研究[D]. 哈尔滨工业大学, 2019.
[6] Roivainen J. Unit-wave response-based modeling of electromechanical noise and vibration of electrical machines[D]. Finland : Helsinki University of Technology, 2009.
[7] Garvey S D, Flem G D L. Tangential forces matter [rotating electrical machines][C]. Ninth International Conference on Electrical Machines and Drives (Conf.Publ. No. 468). 1999: 174–178.
[8] 李晓华, 田晓彤, 汪月飞, 章李烽, 吕舒艺. 分数槽永磁同步电机多物理场电磁振动分析[J]. 微特电机, 2019, 47(11): 19-23.
[9] 郑军强, 赵文祥, 吉敬华, 李浩天. 分数槽集中绕组永磁电机低谐波设计方法综述[J]. 中国电机工程学报, 2020, 40(S1): 272-280.
[10] Zarko D, Ban D, Lipo T A. Analytical calculation of magnetic field distributionin the slotted air gap of a surface permanent-magnet motor using complex relativeair-gap permeance[J]. IEEE Transactions on Magnetics, 2006, 42(7): 1828–1837.
Analysis and suppression of radial and tangential force wave vibration of near-polar tank underwater motor
Li Chang, Xia Jiakuan, Zhang Jinming, Zhao Shengjie
(Shenyang University of Technology, Electrical Engineering, Electric Drive Research Institute)
TM351
A
1003-4862(2022)09-0010-04
2022-03-09
李畅(1996-),女,硕士研究生,研究方向:电机设计。E-mail:1596970254@qq.com

