一道2021年“希望杯”竞赛题的解法探究

林国红

(广东省佛山市乐从中学 528315)

1 题目呈现

题目△ABC是边长为2的等边三角形，顶点A在x轴的非负半轴上滑动，顶点B在y轴的非负半轴上滑动，求△ABC的重心G的轨迹方程.

这是2021年第三十一届“希望杯”全国数学邀请赛高一第2试第17题(压轴题)，本题短小精悍、构思独特，综合考查考生逻辑思维、推理论证、运算、以及分析问题和解决问题等方面的能力，涉及的数学知识与蕴含的数学思想方法非常丰富，值得深入研究.

2 题目解析

解法1 如图1，设∠BAO=θ(0≤θ≤90°)，则A(2cosθ,0),B(0,2sinθ).

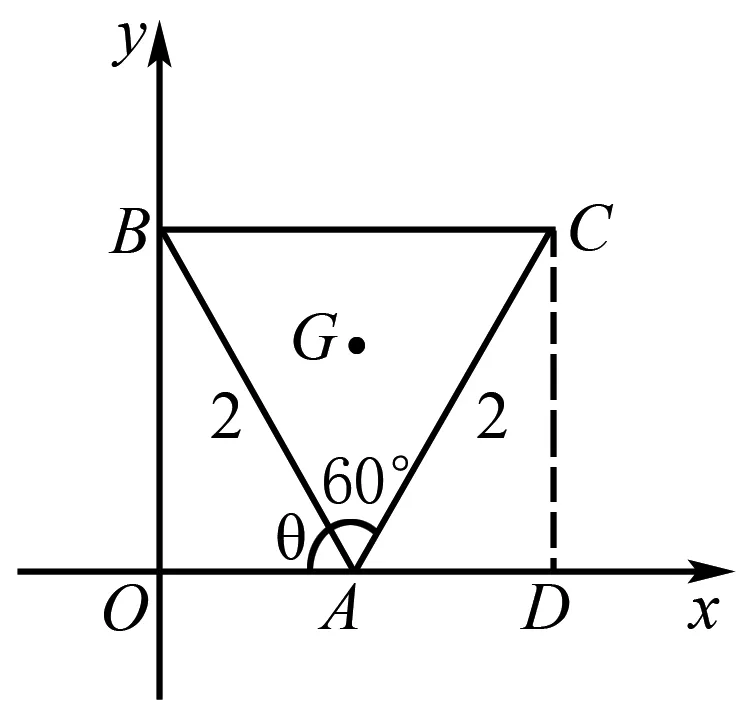
图1

过点C作CD⊥x轴于点D,

可得∠CAD=120°-θ，CD=2sin(120°-θ)，OD=OA+AD=2cosθ+2cos(120°-θ).

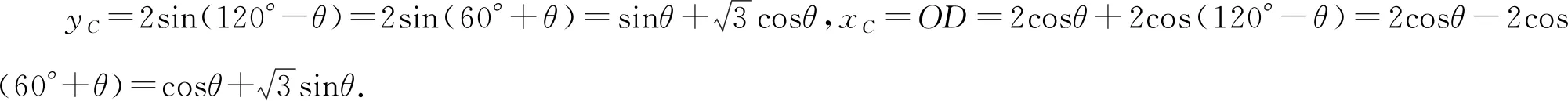
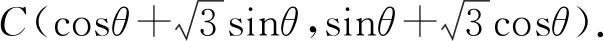
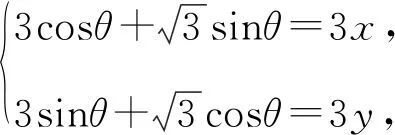
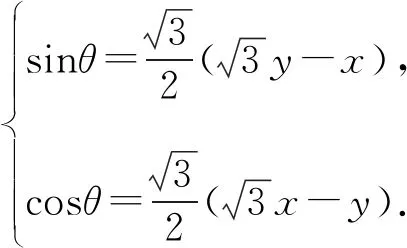
代入sin2θ+cos2θ=1，得

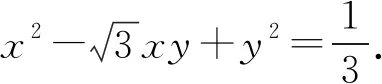
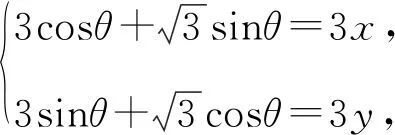
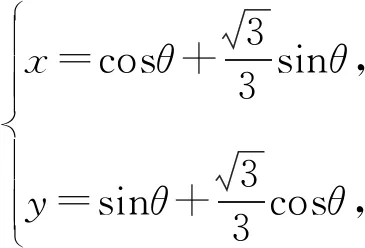
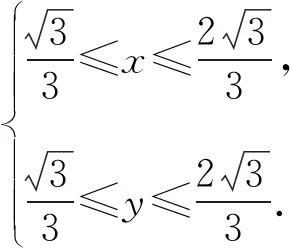
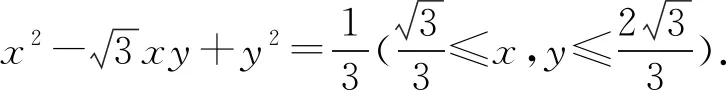
评注解法1利用等边三角形特殊的边角关系，巧妙地将点的坐标以角为参数来表示，再利用三角恒等变换及三角基本关系进行求解，难点是如何合理利用边角关系转化为点的坐标.

解法2如图1，设∠BAO=θ(0≤θ≤90°)，则A(2cosθ,0),B(0,2sinθ).

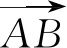
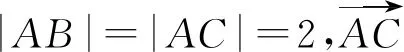
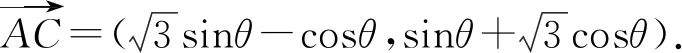
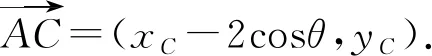
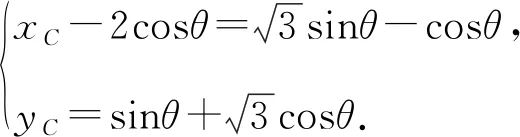
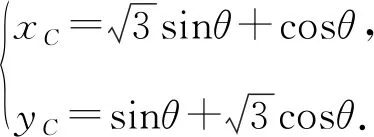
设点G的坐标为G(x,y)，则

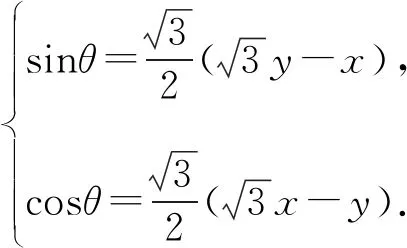
代入sin2θ+cos2θ=1，得

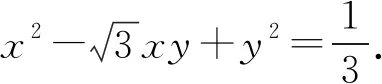
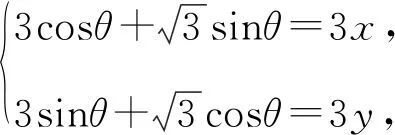
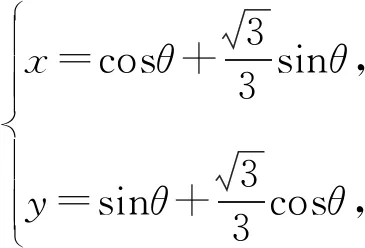
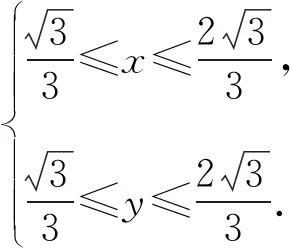
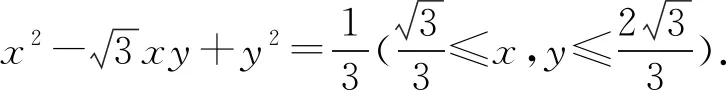
解法3如图1，设A(x0,0),B(0,y0)，则

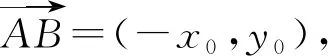
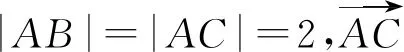
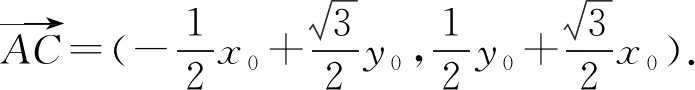
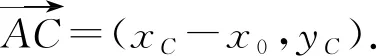
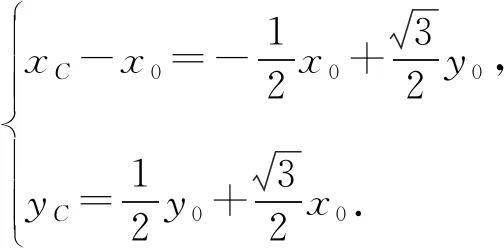
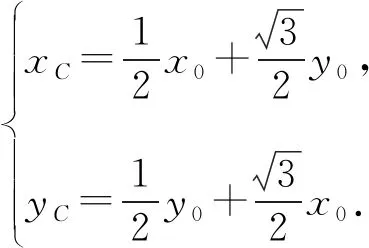
设点G的坐标为G(x,y)，则

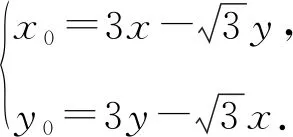
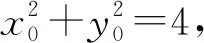
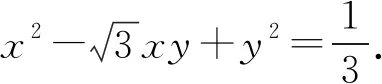
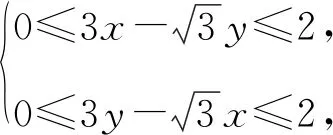
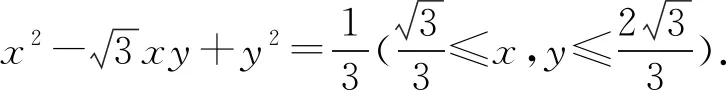
评注解法2与解法3借助向量与复数的相关知识，利用旋转变换的思想进行解答，两种解法建立在同一个解题思路上，从不同的设点角度解决问题，解题方法新颖巧妙，过程简洁.所以在竞赛层面，要重视方法的积累和知识的储备，熟练掌握一些常用的方法与结论，才有可能缩短思维的长度，提高效率，达到事半功倍的效果.

解法4如图2，设AB的中点为E，连接CE.

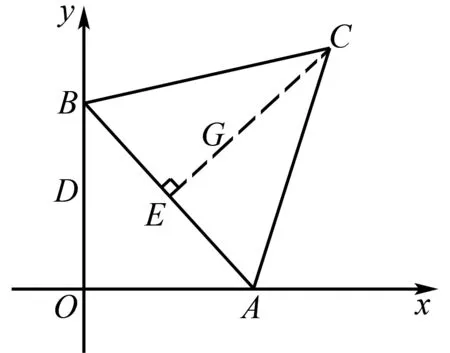
图2

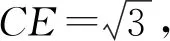
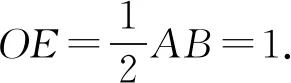
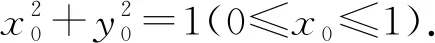
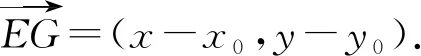
由AB⊥EG，得

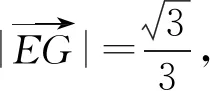
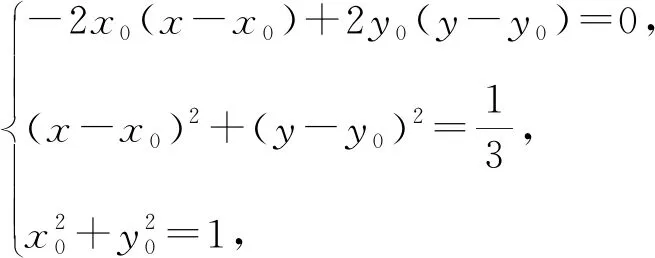
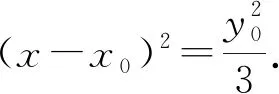
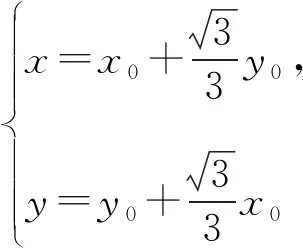
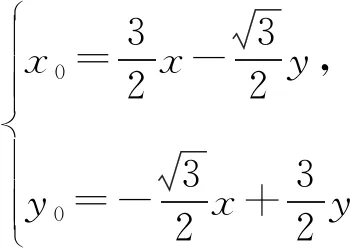
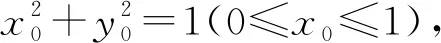
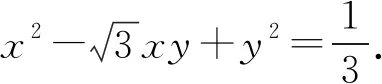
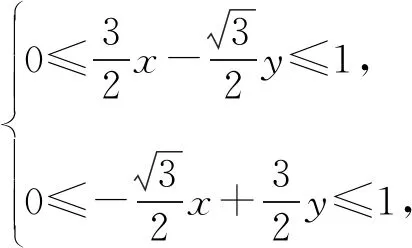
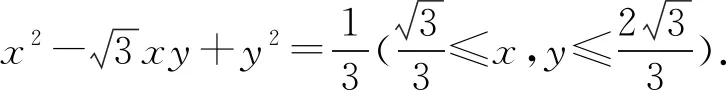
评注解法4借助向量的数量积运算，思路巧妙.向量有着深刻的几何背景，具有良好的“数形结合”特性，是解决几何问题的有力工具.

解法5如图3，设AB的中点为E，连接CE.

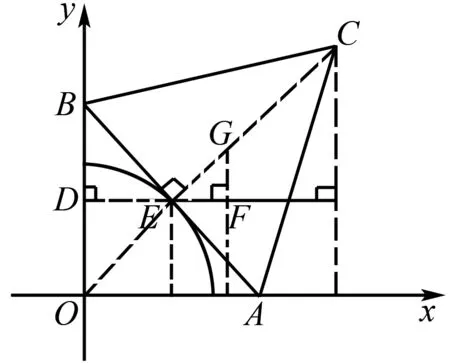
图3

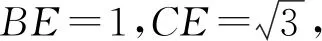
易得△BDE∽△EFG，故

设点E的坐标为E(x0,y0)，因为E是AB的中点，所以BD=y0,DE=x0.

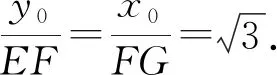
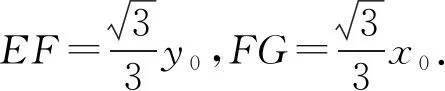
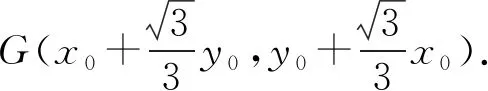
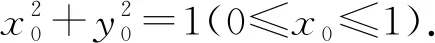
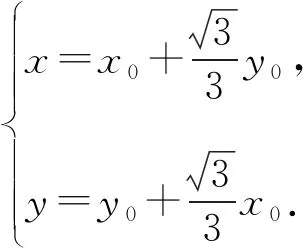
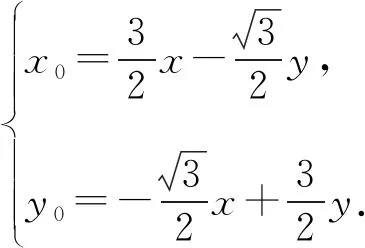
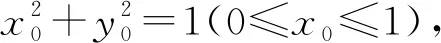
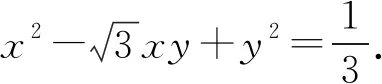
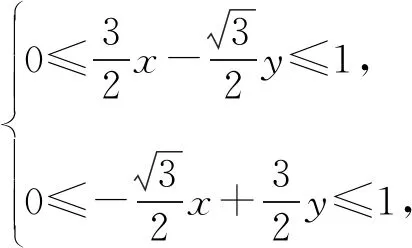
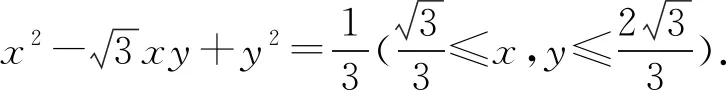
评注解法5借助平面几何的性质进行解答，体现了数形结合的解题思想，运算量较少.解析几何问题的本质仍是几何问题，解题时若能充分把握解析几何的图形特征，挖掘图形相应的几何性质，将解析法与平面几何方法相结合，往往能简化运算，优化解题过程，起到四两拨千斤之功效.

以上的几种解法，从不同的角度出发思考问题，各显神通，这充分体现试题的不拘一格，一道试题考查多种能力、多种思想方法.学数学离不开解题，数学家波利亚曾说：“掌握数学就意味着善于解题.”同时要注意的是，数学问题的解决仅仅只是一半，更重要的是在解题中要善于观察、善于思考、善于转化，只有这样才能将零散的数学知识串联起来，运用自如.