地震加速度时程在时域和频域积分中的对比分析
徐龙辉
(广州南粤地震工程勘察有限公司,广州 510641)
地震加速度时程是对地震进行分析的初始数据之一,其对地震反应谱分析、地震危险性分析等都有着较为明显的影响。因此对初始测得的地震加速度时程信号能否进行准确的分析将会有十分重大的意义。
在实际测试中,进行地震加速度信号采集的时候,往往会因为采集仪器本身以及采集环境的影响而导致采集得到的地震加速度信号,总是会含有不同程度的干扰噪声和直流分量,这些成分虽然不至于太过影响地震加速度的时程分析,但是在积分求速度和位移时程时,因为误差的累积,可能使得速度和位移时程的误差较大甚至完全失真。
通常会采用时域积分或者频域积分这2种方法来对地震加速度时程信号进行分析。
时域积分法是指对地震加速度时程信号直接进行时间上的积分。梯形积分法和辛普森积分法在现实中比较常用,本文采用梯形积分法进行对比分析[1]。
频域积分则是先将地震加速度时程信号通过傅里叶变换转换为频域信号,将信号在频域内进行积分后再通过逆傅里叶变换转换为时域信号,从而得到最终的积分结果[2]。
1 研究方法
1.1 时域积分分析
测得的地震加速度时程信号其实包含了3大部分的信号:实际地震加速度信号a1(t)、干扰噪声a2(t)和常数误差C[3],那么测得的地震加速度时程信号a(t)=a1(t)+a2(t)+C,那么进行一次积分后求得的速度和位移分别如下
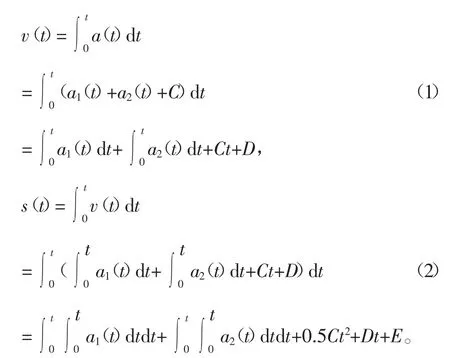
由公式(1)和(2)可以很清楚地看出,通过加速度信号积分得到的速度信号和位移信号存在常数项和一次项的误差,而位移信号还存在二次项的误差,因此在不进行误差处理的情况下,误差会随着积分次数的增多而不断累加。
1.2 频域积分分析
频域内积分是将加速度信号由时域转换到频域内进行处理。主要是通过对加速度信号进行傅里叶变换,之后再进行积分运算,最后通过逆变换将频域信号转换回时域信号。
根据傅里叶变换的积分特性及其逆变换的公式,加速度信号在任一频率的傅里叶分量可以表达为

式中:a(t)为加速度信号在频率ω处的傅里叶分量,其中ω不为0;A为系数
则速度和位移在频率ω处的傅里叶分量可表达为
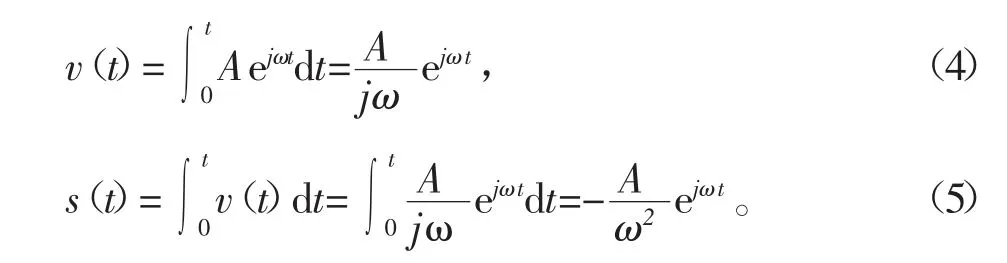
最后根据傅里叶逆变换就能得到相应的速度和位移在时域内的对应数值。
2 实例验证
2.1 EL-Centro波的时域和频域积分
对EL-Centro波(NS向,前52.72 s)分别进行时域和频域的积分,得到速度时程和位移时程的信号图,如图1所示。
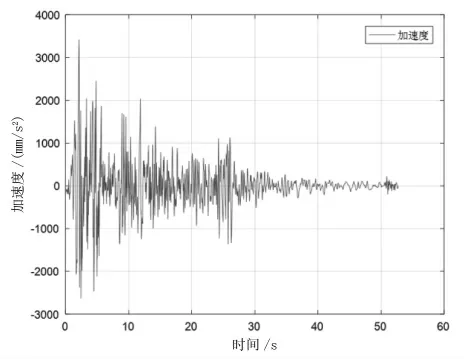
图1 EL-Centro波加速度信号(NS向)
由图2可知加速度信号在一次积分后得到的速度信号,在频域和时域内都保持有较好的一致性,时域有较为明显的基线漂移现象,且随着时间的推移,漂移现象越来越严重;频域积分的初始值不为零。但是整体趋势是与初始加速度信号相一致的。
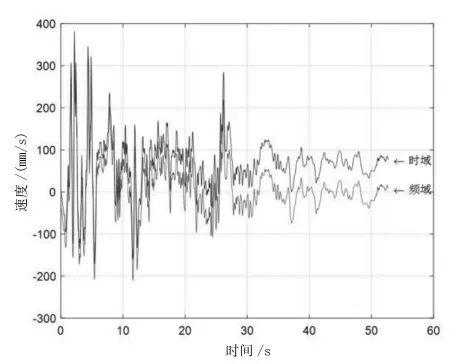
图2 时域和频域内速度积分信号
由图3可知,时域有着非常明显的基线漂移现象,使得位移积分信号完全变形;频域积分的初始值依旧不为零。而二者与初始加速度信号的整体趋势已经不再保持一致。
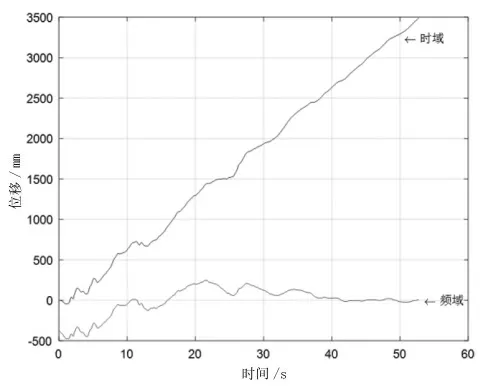
图3 时域和频域内位移积分信号
可见,由加速度通过积分得到的速度信号2种方法基本上可以“保真”,而由加速度通过二次积分得到的位移信号则较为“失真”。
因此,需要对初始加速度数据进行去趋势项滤波处理。
在时间域积分,常用的去趋势项处理方法主要有去均值法、去线性趋势及去多项式趋势[4-5]。因从加速度积分到位移,只需进行二次积分,积分后的数据至少会存在二次项的误差,因此本文利用最小二乘法的原理,对初始加速度数据去除二次项趋势之后再进行时域上的积分[6-7]。
在频率域积分,对初始加速度数据进行滤波。滤波时,尽可能地滤除误差项,对于截止频率的选取就成了重中之重。如果截止频率选取得不合适,那么有可能造成不必要的能量损耗,也有可能滤除的波形不够而达不到滤波的效果。在实践中发现低频截止频率起着关键性的作用,而高频截止频率对滤波起到的作用相当微小。同时在实践中也发现低频截止频率设置在加速度数据开始有较为明显的增大时的频率更为合适,能够有效地去除杂波,同时能量损耗也能控制得比较低[7-8]。该低频截止频率可以通过经傅里叶变换后的频谱图分析得到。
用上述方法对时域去二次项趋势项,对频域高通滤波后得到图4和图5。
由图4和图5可以看出,时域的基线漂移现象明显改善,但是位移积分依旧存在较大的误差,其信号走向与初始加速度信号存在较大的形变;而频域在改善了基线偏移现象的同时还能使波形与初始加速度信号的走向保持较好的一致性。
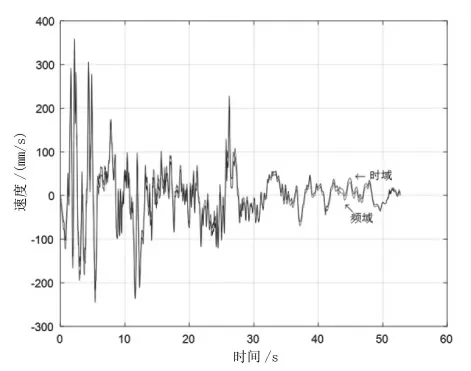
图4 处理后的时域和频域内速度积分信号
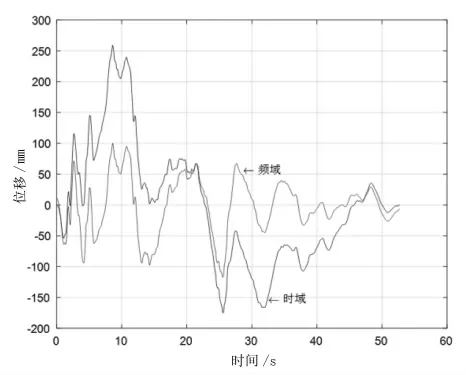
图5 处理后的时域和频域内位移积分信号
2.2 Northridge波的时域和频域积分
对Northridge波(NS向,前30 s)分别进行时域和频域的积分,得到速度时程和位移时程的信号图,如图6所示。
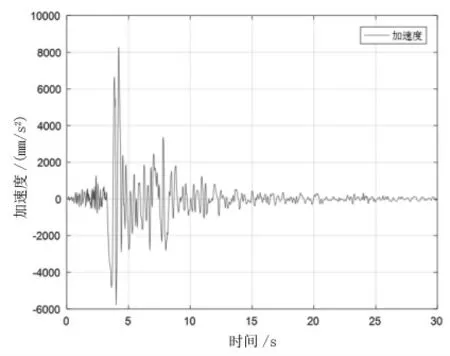
图6 Northridge波加速度信号(NS向)
由图7可知,加速度信号在一次积分后得到的速度信号,在频域和时域内都保持有较好的一致性,基线漂移现象不明显。
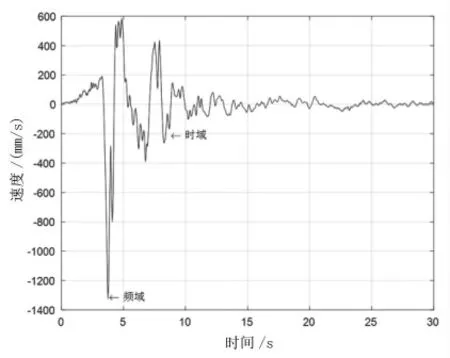
图7 时域和频域内速度积分信号
由图8可知,时域和频域都有着较为明显的基线漂移现象,且随着时间的推移,漂移现象越来越严重;但二者与初始加速度信号的整体趋势保持较好的一致性。
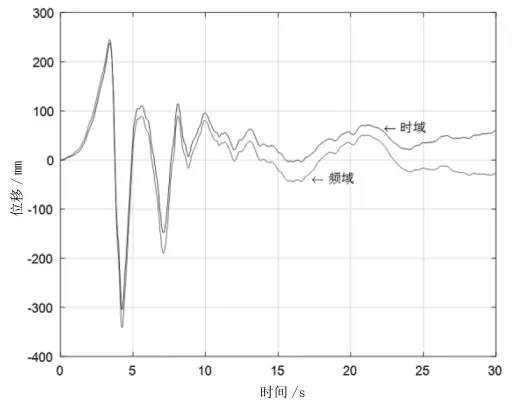
图8 时域和频域内位移积分信号
对时域去二次项趋势项,对频域高通滤波后得到图9和图10。
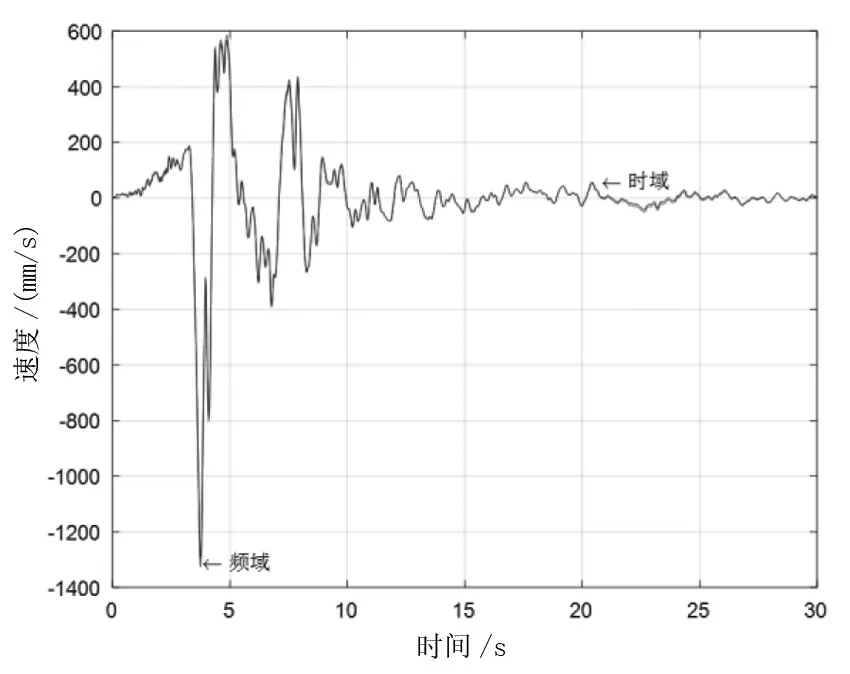
图9 处理后的时域和频域内速度积分信号
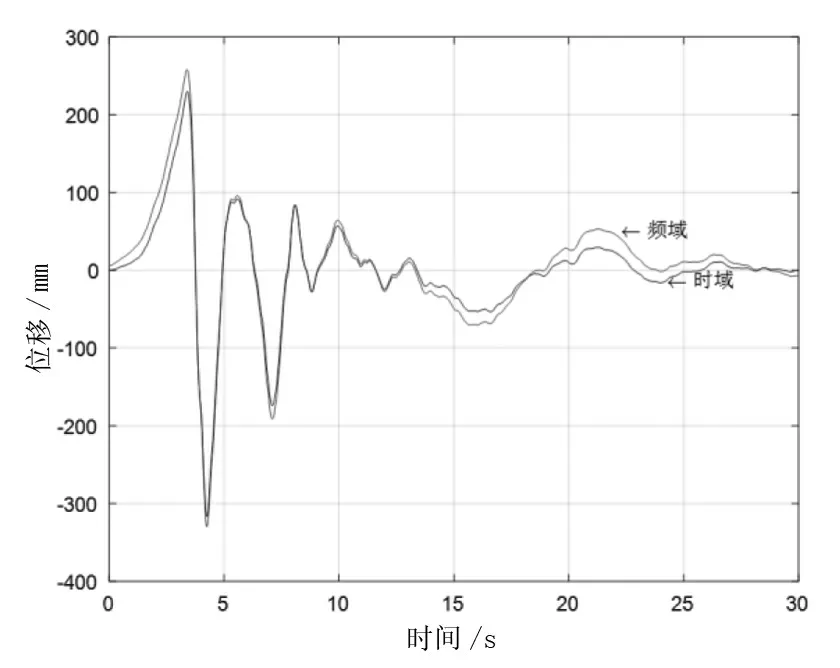
图10 处理后的时域和频域内位移积分信号
由图9和图10可以看出,时域基线漂移现象明显改善,频域则改善相对较小;两者信号走向与初始加速度信号的走向都保持较好的一致性。
3 结论
通过对地震加速度时域积分和频域积分的对比分析,再结合实例验证,可得出以下结论。
(1)时域积分的误差主要来源于趋势项的积分累积,该误差会随着积分次数以及时间的推移而产生基线漂移现象,且积分次数越多、时间越靠后,漂移现象越严重;在进行去二次项趋势后,积分后得到的速度信号能有较为明显的改善,而位移信号虽然能缓解基线漂移现象,但是信号的整体趋势却与初始加速度信号可能存在较大形变。
(2)频域积分能有效地缓解基线漂移现象,且其积分后的信号走向与初始加速度信号都能够保持较好的一致性。相较于时域积分而言,频域积分具有更强的稳定性、准确性和适用性。
(3)频域积分的速度和位移初始值与最终值不一定为零,此处产生的误差与滤波时设置的截止频率有关。同时,进行滤波时,发现低频滤波,即高通滤波,对误差的控制起着关键性的作用,因此选取合适的低频截止频域是频域积分的重中之重,在实践中也发现低频截止频率设置在加速度数据开始有较为明显的增大时的频率更为合适。该低频截止频率可以经傅里叶变换后的频谱图分析得到。

